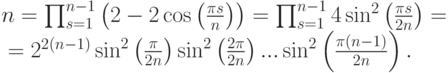Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2020 года; проверки требует 21 правка.
Первообразный корень по модулю m ― целое число g такое, что
и
при
где 
Чтобы не проверять все 


- Является ли
числом взаимно простым с
, и если нет – то это не первообразный корень.
- Так как
– всегда чётное число для всех
, то
имеет как минимум один простой делитель – простое число
, следовательно, для того, чтобы отсеять значительное количество не-корней, достаточно проверить
для числа, подходящего на первообразный корень по модулю
.[1] Если результат +1
m , то g – не корень, в ином случае результат -1
m, когда g – это возможно первообразный корень.
- Далее следует убедиться, что
для всех
, где
– простой делитель числа
, полученный в результате его факторизации.
Свойства[править | править код]
Существование[править | править код]
Первообразные корни существуют только по модулям 
,
где 


Количество[править | править код]
Если по модулю 





Индекс числа по модулю[править | править код]
Для первообразного корня 




Такое число 
Минимальный корень[править | править код]
Исследования Виноградова показали, что существует такая константа 




Математик Виктор Шуп[en] из Университета Торонто показал, что если «Обобщённая гипотеза Римана» верна, то первообразный корень есть среди первых 
История[править | править код]
Первообразные корни для простых модулей 

Примеры[править | править код]
Число 3 является первообразным корнем по модулю 7. Чтобы в этом убедиться, достаточно каждое число от 1 до 6 представить как некоторую степень тройки по модулю 7:
Примеры наименьших первообразных корней по модулю m (последовательность A046145 в OEIS):
| Модуль m | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Первообразный корень | 1 | 2 | 3 | 2 | 5 | 3 | — | 2 | 3 | 2 | — | 2 | 3 |
См. также[править | править код]
- Гипотеза Артина
- Дискретное логарифмирование
- Показатель числа по модулю
Примечания[править | править код]
- ↑ Primitive Root – Competitive Programming Algorithms. cp-algorithms.com. Дата обращения: 27 октября 2020. Архивировано 24 октября 2020 года.
- ↑ Bach, Eric; Shallit, Jeffrey. Algorithmic Number Theory (Vol I: Efficient Algorithms). — Cambridge: The MIT Press, 1996. — P. 254. — ISBN 978-0-262-02405-1.
Литература[править | править код]
- Виноградов И. М. Глава 6. Первообразные корни и индексы // Основы теории чисел. — 1952. — 182 с.
- Нестеренко Ю. В. Глава 7. Первообразные корни и индексы // Теория чисел. — М.: «Академия», 2008. — 464 с.
Ссылки[править | править код]
- «Первообразные корни» на сайте MAXimal Архивная копия от 1 декабря 2011 на Wayback Machine
- Weisstein, Eric W. Primitive Root (англ.) на сайте Wolfram MathWorld.
1
= cos0+i sin0
=
cos+i
sin,
.
Корни
расположены на окружности единичного
радиуса и делят эту окружность на n
равных частей.
Теорема 1.
Все
значения корня n–той
степени из комплексного числа z
можно получить умножением одного из
них на все корни из 1.
Доказательство:
Возьмём
=
=
(cos
+i
sin),
где s–фиксированное
число.
1,
2,…,
n
– так обозначим все корни
.
Домножим
каждый из корней 1,…,
n
на .
Они разные, все являются корнями n–той
степени из z,
ибо (i)n
= z
и их
штук.
Теорема
доказана.
Теорема
2.
Произведение
двух корней n–той степени
из единицы есть корень степени n
из единицы.
Следствие.
Степень
корня n–той
степени из единицы есть корень степени
n
из единицы.
Все
ли корни из 1 равноправны?
n=4
; 1, –1, i,
–i
— корни из единицы.
i;
–i
— первообразные корни; если i
возводить в степени 0, 1, 2, 3, то получим
все корни.
Определение
1.
Корень
n–той
степени из 1 называется первообразным,
если он не даёт единицу в степени меньше,
чем n.
Всегда ли есть первообразный корень?
Всегда!
Например: cos+i
sin.
Упражнение.
Доказать, что корень
n–той
степени
k
= cos
+ i sin
будет
первообразным, если n
и k
— взаимно простые (не имеют общих
делителей отличных от 1).
§6. Числовое поле.
В
множествах Q
R
C
возможны четыре операции +,
–,
, .
Определение
1. Подмножество K
C
множества комплексных чисел C,
состоящее более, чем из одного элемента,
называют числовым полем, если выполняются
следующие условия:
1)
a,
bK
a+bK
, то есть в множестве K
всегда возможно сложение;
-
aK
–aK
; -
a,
bK
abK
, то есть задано умножение в K
(K
замкнуто относительно умножения);
4)
a
0 ; a
-1K.
Из
2) с учётом 1) получаем, что в K
всегда возможно вычитание.
Из
4) с учётом 3) получаем, что в K
всегда возможно деление на число не
равное 0.
Q
— поле рациональных чисел;
R
— поле вещественных чисел;
C
— поле комплексных чисел.
Упражнение 1. Числовое поле всегда бесконечно. Упражнение 2. Любое числовое поле всегда содержит q (множество рациональных чисел).
Пример
поля отличного от Q,
R
и C:
K
= {a+b,
где a
и b
}.
Тема 2. Матрицы и определители.
§1. Сложение матриц. Умножение матрицы на число.
Пусть
К ≠ .
Рассмотрим прямоугольную таблицу из n
строк и m столбцов, состоящую из элементов
К
(1)
aij
— произвольный
элемент таблицы, где i
— номер строки, j
— номер столбца, aij
К
i,j.
Таблицу (1) назовем матрицей размером n
x
m.
Краткая запись (aij)n
x
m.
В будущем
будем рассматривать (1) над числовыми
полями. Матрицы будем обозначать A,B,C,
а
их элементы
соответственно aij
, bij,
cij
.
Определение
1. Две матрицы
(aij),
(bij
) одинаковых
размеров будем называть равными, если
aij
= bij
i,j.
Определение
2. Матрица
называется квадратной, если m=n.
Определение
3.
Квадратная матрица называется
диагональной, если все элементы, стоящие
вне главной диагонали, равны 0.

Определение
4.
Диагональная
матрица, все элементы которой равны
между собой, называется скалярной
матрицей.
Скалярная матрица, у которой элемент,
стоящий на диагонали равен 1, называется
единичной.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Здравствуйте! Есть вопрос по задаче из Фадеева-Соминского на тему “комплексные числа”.
Выписать первообразные корни из 
Я могу выписать например корни.
….
Я могу все это представить в алгебраической форме, не проблема. Но как отобрать из них первообразные корни?
Что такое первообразные корни? Я это не очень понял как-то. В интернете понятного объяснения не нашел, там все кольца, поля, группы, а этого я не проходил. Можно ли как-то без этого найти первообразные корни?
— 26.11.2015, 17:57 —
Но в википедии нашел, что 

Если корень второй степени, то оба корня первообразные
Если корень третьей степени, то все три корня первообразные
Если четвертой степени, то все кроме того, где
Если пятой степени, то все
Если шестой степени, то все, кроме 
— 26.11.2015, 17:59 —
(Оффтоп)
Пока что не очень очевиден смысл первообразных корней? Зачем они?
Аннотация: В данной лекции рассматриваются комплексные корни n-й степени из единицы. Приведены формулы для решения уравнений третьей и четвертой степеней, доказан ряд теорем. Рассмотрен ряд характерных задач, а также приведены задачи для самостоятельного рассмотрения
Комплексные корни n-й степени из единицы
Так как 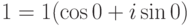

Точки wk являются вершинами правильного n -угольника, вписанного в окружность единичного радиуса с центром в начале координат, при этом одной из вершин этого многоугольника является 1. Например, при n=8
Теорема 2.9.1. Совокупность 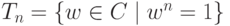
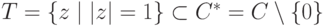
Доказательство.
- Если
, т. е. wn=1, zn=1, то
, поэтому
. Таким образом, на Tn определена операция умножения (очевидно, коммутативная и ассоциативная).
- Ясно, что 1n=1, т. е.
, и 1 – нейтральный элемент в Tn.
- Если
, то wn=1,
и поэтому
.
Замечание 2.9.2. Группа Tn является циклической, т. е. все ее элементы являются степенями одного элемента, называемого циклическим образующим (в качестве одного из циклических образующих можно взять 

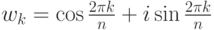
Упражнение 2.9.3. Доказать, что сумма всех k -х степеней корней уравнения xn=1 равна
n, если k делится на n ;
0, если k не делится на n.
Задача 2.9.4. Если 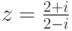
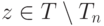
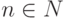
Задача 2.9.5. Доказать, что
а) 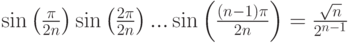
б) 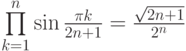
Указание. Пусть
(все корни степени 2n из 1 ).Тогда
(так как xn=-1, x2n=1 ). Но 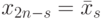
Следовательно,
Полагая x=1, имеем
Пункт б) доказывается аналогично.


















![$sqrt[n]{1}=cos left(dfrac{2pi k}{n}right)+isin left(dfrac{2pi k}{n}right)$ $sqrt[n]{1}=cos left(dfrac{2pi k}{n}right)+isin left(dfrac{2pi k}{n}right)$](https://dxdy-01.korotkov.co.uk/f/0/1/e/01efb68c0b29f58bbbaf1915edf8106682.png)
![$sqrt[2]{1}=cos left(dfrac{2pi k}{2}right)+isin left(dfrac{2pi k}{2}right)=pm 1$ $sqrt[2]{1}=cos left(dfrac{2pi k}{2}right)+isin left(dfrac{2pi k}{2}right)=pm 1$](https://dxdy-02.korotkov.co.uk/f/9/4/e/94edb62ff478e9272534a2f7f0e591b882.png)
![$sqrt[3]{1}=cos left(dfrac{2pi k}{3}right)+isin left(dfrac{2pi k}{3}right)$ $sqrt[3]{1}=cos left(dfrac{2pi k}{3}right)+isin left(dfrac{2pi k}{3}right)$](https://dxdy-01.korotkov.co.uk/f/4/a/0/4a0a332c5e83a9ff44bf98f44e9b5a7782.png)
![$sqrt[4]{1}=cos left(dfrac{2pi k}{4}right)+isin left(dfrac{2pi k}{4}right)$ $sqrt[4]{1}=cos left(dfrac{2pi k}{4}right)+isin left(dfrac{2pi k}{4}right)$](https://dxdy-03.korotkov.co.uk/f/e/0/a/e0a5c4c50e63d97f9bc9f2a046122de882.png)

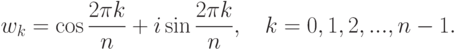

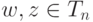 , т. е.
, т. е. 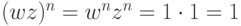 , поэтому
, поэтому  . Таким образом, на
. Таким образом, на 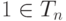 , и
, и 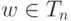 , то
, то 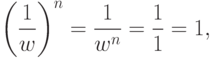
 .
.
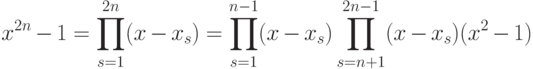
![begin{mult}
x^{2n}-1=(x^2-1)smash[b]{prod_{s=1}^{n-1}(x-x_s)(x-bar x_s)}={}\
{}=(x^2-1)prod_{s=1}^{n-1}left(x^2-2xcosfrac{pi s}{n}+1right).
end{multl}](https://intuit.ru/sites/default/files/tex_cache/9a6b233beb02b4f592e621bfdeef0bd9.png)