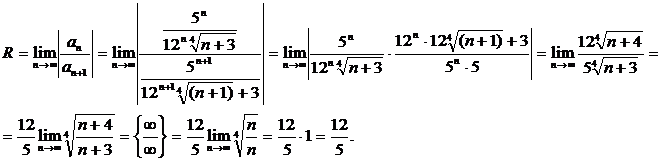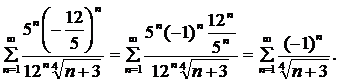Исследование степенного ряда на сходимость
Дан степенной ряд . Написать первые три члена ряда, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение. – общий член ряда. Подставив в эту формулу n значения 1, 2, 3, …, можно найти любой член ряда:
,
,
.
Степенной ряд в общем виде записывается следующим образом: , где an – формула числовых коэффициентов. Для данного ряда
.
Областью сходимости степенного ряда является интервал (-R;R), где 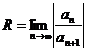
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу .
Теперь проверим сходимость ряда на концах этого интервала.
Пусть получаем ряд
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница:


– точка сходимости.
При исходный ряд принимает вид:

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, – точка расходимости.
Таким образом, данный степенной ряд является сходящимся при .
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Ряды для чайников. Примеры решений
Всех
выживших приветствую на втором курсе!
На этом уроке, а точнее, на серии уроков,
мы научимся управляться с рядами. Тема
не очень сложная, но для ее освоения
потребуются знания с первого курса, в
частности, необходимо понимать, что
такое предел,
и уметь находить простейшие пределы.
Впрочем, ничего страшного, по ходу
объяснений я буду давать соответствующие
ссылки на нужные уроки. Некоторым
читателям тема математических рядов,
приемы решения, признаки, теоремы могут
показаться своеобразными, и даже
вычурными, нелепыми. В этом случае не
нужно сильно «загружаться», принимаем
факты такими, какими они есть, и просто
учимся решать типовые, распространенные
задания.
Рекомендую
следующий порядок изучения темы:
1) Ряды
для чайников (эта
статья).
2) Признак
Даламбера. Признаки Коши.
3) Знакочередующиеся
ряды. Признак Лейбница.
Понятие
числового положительного ряда
В
общем виде положительный
числовой ряд можно
записать так:
.
Здесь:
–
математический значок суммы;
– общий
член ряда (запомните
этот простой термин);
–
переменная-«счётчик». Запись
обозначает,
что проводится суммирование от 1 до
«плюс бесконечности», то есть, сначала
у нас
,
затем
,
потом
,
и так далее – до бесконечности. Вместо
переменной
иногда
используется переменная
или
.
Суммирование не обязательно начинается
с единицы, в ряде случаев оно может
начинаться с нуля
,
с двойки
либо
с любого натурального
числа.
В
соответствии с переменной-«счётчиком»
любой ряд можно расписать развёрнуто:
–
и так далее, до бесконечности.
Будем
считать, что ВСЕ слагаемые
–
это неотрицательные
ЧИСЛА.
То есть, на данном уроке речь пойдет
о положительных
числовых рядах.
Пример
1
Записать
первые три члена ряда
Это
уже, кстати, «боевое» задание – на
практике довольно часто требуется
записать несколько членов ряда.
Сначала
,
тогда:
Затем
,
тогда:
Потом
,
тогда:
Процесс
можно продолжить до бесконечности, но
по условию требовалось написать первые
три члена ряда, поэтому записываем
ответ:
Пример
2
Записать
первые три члена ряда
Это
пример для самостоятельного решения,
ответ в конце урока
Даже
для сложного на первый взгляд ряда не
составляет трудности расписать его в
развернутом виде:
Пример
3
Записать
первые три члена ряда
На
самом деле задание выполняется
устно: мысленно
подставляем в общий член ряда сначала
,
потом
и
.
В итоге:
Ответ
оставляем в таком виде, полученные
члены ряда лучше не упрощать,
то естьне
выполнять действия:
,
,
.
Почему? Ответ в виде
гораздо
проще и удобнее проверять преподавателю.
Иногда
встречается обратное задание
Пример
4
Записать
сумму в свёрнутом виде с общим членом
ряда
Здесь
нет какого-то четкого алгоритма
решения, закономерность
нужно просто увидеть.
В
данном случае:
Для
проверки полученный ряд
можно
«расписать обратно» в развернутом виде.
А
вот пример чуть сложнее для самостоятельного
решения:
Пример
5
Записать
сумму в свёрнутом виде с общим членом
ряда
Выполнить
проверку, снова записав ряд в развернутом
виде
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
(схема 48)
Числовым рядом (или просто рядом) называется бесконечная сумма вида

где 
ряда, un –
общим
членом ряда.
Если известен общий член ряда как функция его номера n: un=f(n), то ряд
считают заданным.
Сумма первых n членов ряда (9.1) называется n-ой частичной суммой ряда Sn, то есть Sn = u1 + u2 +…+ un.
Рассмотрим последовательность частичных сумм ряда
(9.1):

Если существует конечный предел 
частичных сумм (9.2), то этот предел называют суммой
ряда, а сам ряд – сходящимся числовым рядом. При этом
записывают:
Если 

суммы не имеет.
Ряд 
ряда после n-го члена или n-ым остатком ряда.
Сформулируем некоторые свойства числовых рядов.
1. Если ряд (9.1) сходится и его сумма равна S, то ряд

где
c – произвольное
число, также сходится и его сумма равна cS. Если же ряд (9.1) расходится и c ≠ 0, то и ряд (9.3) расходится.
2. Если сходится ряд (9.1) и сходится ряд 

соответственно S1± S2.
Следствие.
Сумма (разность)
сходящегося и расходящегося рядов есть расходящийся ряд
Примечание. Сумма (разность) двух расходящихся рядов
может быть как сходящимся, так и расходящимся рядом.
3. Если к ряду (9.1) прибавить или отбросить конечное
число членов, то полученный ряд и ряд (9.1) сходятся или расходятся
одновременно.
Следствие. Если ряд (9.1) сходится, то
его n-ый остаток rn
стремится к нулю при n→∞, то есть 
Теорема 9.1
(необходимый признак сходимости числового ряда). Если ряд (9.1)
сходится, то его общий член un стремится к нулю при неограниченном возрастании n, то есть 
Следствие (достаточное
условие расходимости ряда). Если 
существует, то ряд расходится
Таким образом, из того, что общий член
ряда стремится к нулю при n→∞, еще не следует, что ряд сходится.
Пример 9.1. Исследовать на сходимость ряд 
Решение. Вычислим предел общего члена ряда:

Следовательно, заданный ряд расходится
Во многих случаях на вопрос о
сходимости или расходимости числового ряда можно ответить с помощью достаточных
признаков.
Сходимость или расходимость знакоположительного ряда
часто устанавливается путем сравнения его с другим рядом, о котором известно,
сходится он или нет. Подобное сравнение базируется на теоремах 9.2 и 9.3.
Теорема 9.2
(признак сравнения числовых знакоположительных рядов). Пусть даны два знакоположительных ряда


Если для всех n, начиная с некоторого номера N, выполняется неравенство 
а из расходимости ряда (9.4) следует расходимость ряда (9.5)
В этом случае ряд (9.4) называется минорантным,
а ряд (9.5) – мажорантным рядом.
Пример 9.2. Исследовать на сходимость ряд 
Решение. Общий член заданного ряда

(мажорантный) расходится и подавно
Теорема 9.3.
(признак сравнения в предельной форме)
Пусть даны два знакоположительных ряда (9.4) и (9.5).
Если существует конечный, отличный от нуля, предел 
Теорема 9.4
(признак Даламбера). Если в ряде (9.1) с положительными членами отношение последующего члена ряда к
предыдущему при n→∞ имеет конечный или бесконечный предел 
l<1 ряд сходится и расходится
при l>1
Примечание. Если l=1, то ряд (9.1) может быть как сходящимся, так и
расходящимся 
Признак Даламбера целесообразно применять, когда общий
член ряда содержит факториалы и показательные выражения.
Пример 9.3. Исследовать на сходимость ряд
Решение. Согласно теореме 9.4 вычислим величину 
заданный ряд сходится
Теорема 9.5
(радикальный признак Коши). Если для ряда (9.1) с положительными членами существует
конечный или бесконечный предел 
l<1 ряд сходится и расходится
при l>1
Пример 9.4. Исследовать на сходимость ряд 
Решение. Учитывая теорему 9.5 и второй замечательный предел (3.13), вычисляем:

радикальному признаку Коши заданный ряд сходится
Теорема 9.6
(интегральный признак Коши). Если
члены знакоположительного числового ряда 
представлены как числовые значения некоторой непрерывной монотонно убывающей на
промежутке [1;∞) функции f(x) так, что u1= f(1), u2= f(2), …,
un= f(n), …, то если 
и ряд (9.1); если
расходится также и ряд (9.1) 
Пример 9.5. Исследовать на сходимость ряд 
Решение. Для исследования ряда на сходимость применим интегральный признак Коши – рассмотрим несобственный интеграл

Так как несобственный интеграл от общего члена ряда сходится, то и исходный ряд также сходится (согласно теореме 9.6)
Особое значение в теории числовых рядов (в частности,
при их сравнении) имеет обобщенный гармонический ряд

где
p>0 –
действительное число. Для
исследования ряда (9.6) применим теорему 9.6 (интегральный признак Коши).
Рассмотрим функцию 


При p = 1
имеем гармонический ряд 

Примечание. Знакоотрицательный ряд переходит в
знакоположительный путем умножения его
на (–1), что не влияет на сходимость
ряда
Помимо знакоположительных числовых рядов существует
важный класс знакопеременных рядов, в которых члены ряда имеют произвольные
знаки.
Числовой ряд 
бесконечное множество отрицательных членов, называется знакопеременным.
Теорема 9.7
(общий достаточный признак сходимости). Пусть
дан знакопеременный ряд
u1 + u2 +…+ un (9.7)
Если сходится ряд

составленный
из модулей членов данного ряда, то сходится и сам знакопеременный ряд (9.7)
Знакопеременный ряд называется абсолютно сходящимся,
если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если
сам он сходится, а ряд, составленный из модулей его членов, расходится.
Сформулируем основные свойства абсолютно сходящихся
рядов.
1. Если ряд абсолютно сходится и имеет сумму S, то ряд,
полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и
исходный ряд.
2. Абсолютно сходящиеся ряды с суммами S1 и S2 можно
почленно складывать (вычитать). В результате получается абсолютно сходящийся
ряд, сумма которого равна S1 + S2 (S1 – S2).
3. Произведение двух абсолютно сходящихся рядов с
суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1 ∙ S2.
Примечание. В случае условно сходящихся рядов подобные свойства,
вообще говоря, места не имеют.
Используя указанные свойства, математические действия и операции производят только над абсолютно сходящимися
рядами. Для установления абсолютной сходимости используют все признаки
сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
Частным случаем знакопеременных рядов являются знакочередующиеся
ряды, члены которых имеют строго
чередующиеся знаки:

где
un>0 для всех 
Для знакочередующихся рядов имеет место следующий
достаточный признак сходимости.
Теорема 9.8
(признак Лейбница). Знакочередующийся
ряд (9.9) сходится, если последовательность абсолютных величин его членов монотонно убывает (u1 > u2 > u3>…> un>) и общий член ряда по абсолютной величине стремится к
нулю при n→∞, то есть 
Пример 9.6. Исследовать на сходимость ряд 
Решение. Это знакочередующийся ряд, для которого выполняются
условия теоремы 9.8. Действительно, предел общего члена ряда 
убывают по абсолютной величине:
составленный из модулей его членов, то есть ряд 
является гармоническим. Значит, заданный по условию знакочередующийся ряд
сходится условно
Ряд, членами которого являются функции от переменной x, называется функциональным:

Придавая x определённое значение x0, мы
получим числовой ряд 
Если полученные числовой ряд сходится, то точка x0 называется точкой сходимости ряда (9.10); если
же ряд расходится – точкой расходимости функционального ряда. Совокупность числовых
значений аргумента x, при которых функциональный ряд сходится, называется
его областью
сходимости.
В области сходимости функционального ряда его сумма
является некоторой функцией от x: S= S(x), которая определяется равенством:

ряда.
Частным случаем
функционального ряда является степенной ряд, члены которого представляют
собой степенные функции аргумента x:

Действительные (или комплексные) числа
ряда (9.11), 
переменная.
Ряд (9.11) называется разложением по степеням x. На практике часто работают со
степенным рядом, разложенным по степеням (x
– x0):

где x0 –
некоторое постоянное число.
Рассмотрим вопрос о нахождении области сходимости
степенного ряда.
Теорема 9.9
(Абеля о сходимости степенного ряда). Если
степенной ряд сходится при некотором значении x0 ≠ 0, то
он абсолютно сходится при всех значениях x, удовлетворяющих неравенству |x|<| x0|; если ряд
(9.11) расходится при x = x1, то он
расходится при всех x,
удовлетворяющих неравенству |x|>| x1|
Из теоремы Абеля следует, что если x0 ≠ 0 есть точка сходимости степенного ряда, то интервал (–|x0|;|x0|) весь
состоит из точек сходимости данного ряда; при всех значениях x вне этого
интервала ряд (9.11) расходится (рис. 9.1). Интервал (–|x0|;|x0|)
называют интервалом сходимости степенного ряда. Положив |x0|=R, интервал сходимости можно записать в виде (–R;R). Число R называют радиусом
сходимости степенного ряда, то есть R > 0 – это
такое число, что при всех x, для которых |x| < R,
ряд (9.11) абсолютно сходится, а при |x| > R
ряд расходится.
Если ряд (9.11) сходится в одной точке x0 = 0, то полагают, что R=0. Если же он сходится при всех действительных
значениях x, то его радиус сходимости R=∞.
На практике радиус сходимости степенного ряда (9.11)
отыскивают с помощью признака Даламбера. Для этого составляют ряд из модулей
членов ряда:

признак Даламбера. Допустим, что существует предел

По теореме 9.4 ряд сходится, если
которых
модулей членов ряда (9.11), расходится при тех значениях x, для
которых 
вычисляется по формуле:

С помощью радикального признака Коши (теоремы 9.5) можно
показать, что радиус сходимости также вычисляется по формуле:

Примечание. Интервал сходимости степенного ряда (9.12) находят из
неравенства |x– x0| < R; он имеет вид (x0–R; x0+R)
Пример 9.7. Найти область сходимости ряда 
Решение. Воспользуемся формулой (9.13) 

Следовательно,
данный ряд абсолютно сходится в единственной точке х = 0.
Область
сходимости степенного ряда (9.11) уточняют на концах полученного интервала
сходимости, симметричного относительно начала координат. На его левом конце,
при 
знакочередующийся числовой ряд, сходимость которого исследуют с помощью
признака Лейбница (теорема 9.8). На правом конце интервала сходимости, при x=R получают
числовой ряд с положительными членами, который исследуют на сходимость с
помощью рассмотренных выше достаточных признаков – теорем
9.2-9.6. Если при 
сходящийся числовой ряд, то
соответствующую точку включают в область сходимости степенного ряда. Если при 
расходящийся числовой ряд, то
соответствующую точку включают в область расходимости степенного ряда.
Уточненный на концах интервал сходимости представляет собой область сходимости
степенного ряда (9.11).
Пример 9.8. Написать первые три члена ряда 
Решение. Беря последовательно n = 1, 2, 3, …, запишем данный ряд в виде:
Для нахождения области сходимости ряда применим
признак Даламбера:

Данный ряд сходится абсолютно при тех значениях x, которые удовлетворяют неравенству

Исследуем сходимость ряда на концах полученного
интервала.
При 
вид 
величина его общего члена стремится к нулю при n→∞; члены ряда убывают по абсолютной
величине. Следовательно, по признаку
Лейбница этот ряд сходится. Значит, 
сходимости данного ряда.
При 

сходимости Коши. Рассмотрим несобственный интеграл

Так как несобственный интеграл сходится, то сходится и
исследуемый ряд. Значит, при 
Таким образом,
по условию ряда
Вопросы для самопроверки
Основные понятия. Запись нескольких первых членов ряда. Свойства числовых рядов.
Содержание темы:
- Понятие числового ряда. Общий член ряда.
- Частичная сумма ряда. Сходящиеся и расходящиеся ряды. Остаток ряда.
- Некоторые свойства числовых рядов.
Понятие числового ряда. Общий член ряда.
Пусть задана некая бесконечная последовательность чисел: ${u_n}$: $u_1$, $u_2$, $u_3$,…, $u_n$,… .
Бесконечная сумма $u_1+u_2+ldots+u_n+ldots$, составленная из элементов числовой последовательности ${u_n}$, называется числовым рядом.
Числа $u_1$, $u_2$, $u_3$ и т.д. именуют членами ряда. Например, $u_1$ – первый член ряда, $u_2$ – второй член ряда, $u_{78}$ – семьдесят восьмой член ряда. Выражение $u_n$ называют общим членом ряда.
Для примера рассмотрим последовательность $left{frac{3^n}{5n+9}right}$ и составим соответствующий числовой ряд. Чтобы не разрывать изложение, данный пример я скрыл под примечание.
Пример числового ряда: показатьскрыть
Однако чаще всего развёрнутую запись: $u_1+u_2+ldots+u_n+ldots$ не используют. Её сокращают в такую форму: $sumlimits_{n=1}^{infty}u_n$. Обе записи эквивалентны:
$$
sumlimits_{n=1}^{infty}u_n=u_1+u_2+ldots+u_n+ldots
$$
Если для вас знак $sum$ требует пояснений, то советую развернуть примечание.
Что обозначает знак $sum$? показатьскрыть
Вовсе не обязательно нижний предел суммирования будет равен единице. Он может равняться любому целому числу, просто в большинстве случаев начальное значение индекса суммирования берут равным $n=1$. Впрочем, нижний предел суммы всегда можно изменить (см. пример №3).
Пример №1
Записать первые четыре члена ряда $sumlimits_{n=1}^{infty}frac{3^n}{ncdotsqrt{n}}$. Указать общий член ряда.
Решение
Чтобы записать несколько первых членов ряда, достаточно подставить в выражение $frac{3^n}{ncdotsqrt{n}}$, расположенное под знаком суммы, числа $n=1$, $n=2$, $n=3$ и т.д.:
$$
sumlimits_{n=1}^{infty}frac{3^n}{ncdotsqrt{n}}=frac{3^1}{1cdotsqrt{1}}+frac{3^2}{2cdotsqrt{2}}+frac{3^3}{3cdotsqrt{3}}+frac{3^4}{4cdotsqrt{4}}+ldots=3+frac{9}{2sqrt{2}}+frac{9}{sqrt{3}}+frac{81}{8}+ldots
$$
А можно просто написать, что $u_1=3$, $u_2=frac{9}{2sqrt{2}}$, $u_3=frac{9}{sqrt{3}}$, $u_4=frac{81}{8}$.
Мы имеем ряд вида $sumlimits_{n=1}^{infty}u_n$. Нижний предел суммирования нашего ряда равен $1$, поэтому общий член ряда записан под знаком суммы. Вот он: $u_n=frac{3^n}{ncdotsqrt{n}}$.
Полагаю, сразу же возникнет вопрос: а что будет, если нижний предел суммирования не равен единице? Совпадёт ли выражение под знаком суммы с общим членом ряда? Ответ в общем случае отрицательный: скорее всего, не совпадёт. Советую глянуть пример №2, чтобы выяснить, что же будет в этом случае. Впрочем, в подавляющем большинстве учебных примеров нижний предел суммирования берут равным именно единице.
Подставляя в равенство $u_n=frac{3^n}{ncdotsqrt{n}}$ вместо $n$ любой номер, мы получим соответствующий член ряда. Например, подставляя $n=4$, получим четвёртый член ряда, а подставляя $n=31$ – тридцать первый член ряда:
$$
u_4=frac{3^4}{4cdotsqrt{4}}=frac{81}{8};; u_{31}=frac{3^{31}}{31cdotsqrt{31}}.
$$
Как видите, если известен общий член ряда, то легко записать член ряда с каким угодно номером, – достаточно лишь подставить вместо $n$ требуемый номер. Гораздо сложнее обратная задача: по нескольким заданным первым членам ряда записать общий член, однако этому вопросу посвящена иная тема.
Кстати сказать, нам совершенно неважно, задан ли номер члена ряда числом или выражением. Например, член ряда с номером $n=k^2+3k-1$ будет таким:
$$
u_{k^2+3k-1}=frac{3^{k^2+3k-1}}{(k^2+3k-1)cdotsqrt{k^2+3k-1}}.
$$
А член ряда с номером $n+1$ будет таким:
$$
u_{n+1}=frac{3^{n+1}}{(n+1)cdotsqrt{n+1}}.
$$
Ответ: Общий член ряда: $u_n=frac{3^n}{ncdotsqrt{n}}$. Первые четыре члена ряда: $u_1=3$, $u_2=frac{9}{2sqrt{2}}$, $u_3=frac{9}{sqrt{3}}$, $u_4=frac{81}{4sqrt{4}}$.
Пример №2
Записать первые пять членов ряда $sumlimits_{n=3}^{infty}frac{1}{(n-1)ln(n-1)}$. Указать общий член ряда.
Решение
Суммирование в нашем случае начинается при $n=3$ (т.е. нижний предел суммирования равен 3), поэтому чтобы записать первые пять членов ряда нужно подставить $n=3$, $n=4$, $n=5$, $n=6$, $n=7$ в выражение $frac{1}{(n-1)ln(n-1)}$:
begin{aligned}
& u_1=frac{1}{(3-1)ln(3-1)}=frac{1}{2ln 2};\
& u_2=frac{1}{(4-1)ln(4-1)}=frac{1}{3ln 3};\
& u_3=frac{1}{(5-1)ln(5-1)}=frac{1}{4ln 4};\
& u_4=frac{1}{(6-1)ln(6-1)}=frac{1}{5ln 5};\
& u_5=frac{1}{(7-1)ln(7-1)}=frac{1}{6ln 6}.
end{aligned}
Теперь нужно указать общий член ряда. Казалось бы, всё просто: вот он, этот общий член – стоит под знаком суммы. Просто перепишем и всё:
$$
u_n=frac{1}{(n-1)ln(n-1)}.
$$
Однако такая формула некорректна. Чтобы это проиллюстрировать, давайте подставим в формулу $u_n=frac{1}{(n-1)ln(n-1)}$ число $n=4$. Мы получим следующее:
$$
u_4=frac{1}{(4-1)ln(4-1)}=frac{1}{3ln 3}.
$$
Мы получили вовсе не то, что нужно! Четвёртый член ряда был найден ранее: $u_4=frac{1}{5ln 5}$. Формула $u_n=frac{1}{(n-1)ln(n-1)}$ дала сбой. Почему? Ответ на данный вопрос прост: дело в том, что значение индекса суммирования (т.е. значение переменной $n$) не совпадает с номером члена ряда. И это неудивительно, ибо нумерация членов ряда начинается с единицы, а первое значение индекса $n=3$. Поэтому под знаком суммы стоит вовсе не общий член ряда:
Заметьте, что число, которое мы подставляем в выражение $frac{1}{(n-1)ln(n-1)}$, на 2 больше, чем номер члена ряда. Т.е. если номер равен $n$, то в выражение $frac{1}{(n-1)ln(n-1)}$ пойдёт число $n+2$. Соответственно, общий член ряда имеет такой вид:
$$
u_n=frac{1}{left((n+2)-1right)lnleft((n+2)-1right)}=frac{1}{(n+1)ln(n+1)}.
$$
Вот теперь общий член ряда записано верно. Например, для $n=4$ согласно формуле $u_n=frac{1}{(n+1)ln(n+1)}$ получим:
$$
u_4=frac{1}{(4+1)ln(4+1)}=frac{1}{5ln 5}.
$$
Можно, кстати, и исходный ряд переписать по-иному, начав суммирование при $n=1$:
$$
sumlimits_{n=3}^{infty}frac{1}{(n-1)ln(n-1)}=sumlimits_{n=1}^{infty}frac{1}{(n+1)ln(n+1)}
$$
Изменение нижнего предела суммирования (т.е. начального значения $n$) никоим образом не влияет на сам ряд. Изменяется лишь форма записи, но не содержание суммы. Можно было вообще изменить значение нижнего предела суммирования в самом начале решения.
Ну, а теперь немного о реалиях: нередко на такие “мелочи” внимания не обращают. И автор книги или методички по высшей математике так и пишет: $u_n=frac{1}{(n-1)ln(n-1)}$, ничуть не озаботясь тем, что эта формула даёт неверные результаты (а при $n=1$ и $n=2$ значение выражения $frac{1}{(n-1)ln(n-1)}$ вообще не определено). И это может привести к печальным ошибкам: например, к сбоям в программе. Поэтому с нумерацией желательно обращаться крайне внимательно. При необходимости нижний предел суммирования можно поменять в самом начале решения.
Ответ: Общий член ряда: $u_n=frac{1}{(n+1)ln(n+1)}$. Первые пять членов: $u_1=frac{1}{2ln 2}$, $u_2=frac{1}{3ln 3}$, $u_3=frac{1}{4ln 4}$, $u_4=frac{1}{5ln 5}$, $u_5=frac{1}{6ln 6}$.
Пример №3
Для ряда $sumlimits_{n=4}^{infty}frac{7n+5}{2^{4n-1}cdot n}$ изменить нижний предел суммирования на 1. Указать общий член ряда.
Решение
Нижний предел суммирования равен 4, т.е. начальное значение индекса $n$ равно четырём. Введём новый индекс таким образом, чтобы его начальное значение равнялось 1. Этот новый индекс суммирования обозначим буквой $t$.
Итак, если $n=4$, то $t=1$, т.е. $n=t+3$. Подставляем в $frac{7n+5}{2^{4n-1}cdot n}$ вместо $n$ выражение $t+3$. При этом не забываем, что новый индекс $t$ изменяется с 1:
$$sumlimits_{n=4}^{infty}frac{7n+5}{2^{4n-1}cdot n}=sumlimits_{t=1}^{infty}frac{7(t+3)+5}{2^{4(t+3)-1}cdot (t+3)}=sumlimits_{t=1}^{infty}frac{7t+26}{2^{4t+11}cdot (t+3)}.$$
В принципе, полученное выражение $sumlimits_{t=1}^{infty}frac{7t+26}{2^{4t+11}cdot (t+3)}$ можно так и оставить. Однако обычно новую букву $t$ не вводят, а продолжают работать со “старым” обозначением индекса, т.е. с $n$. В самом деле, разве что-то изменится, если вместо одной буквы подставить иную?
$$
sumlimits_{t=1}^{infty}frac{7t+26}{2^{4t+11}cdot (t+3)}=sumlimits_{n=1}^{infty}frac{7n+26}{2^{4n+11}cdot (n+3)}
$$
Если пропустить все промежуточные выкладки, то мы приходим к простому равенству:
$$
sumlimits_{n=4}^{infty}frac{7n+5}{2^{4n-1}cdot n}=sumlimits_{n=1}^{infty}frac{7n+26}{2^{4n+11}cdot (n+3)}.
$$
Можете проверить этот результат, найдя несколько первых членов суммы в левой и правой частях равенства.
Так как нижний предел суммы $sumlimits_{n=1}^{infty}frac{7n+26}{2^{4n+11}cdot (n+3)}$ равен 1, то под знаком суммы расположен общий член ряда, т.е. $u_n=frac{7n+26}{2^{4n+11}cdot (n+3)}$.
Ответ: $sumlimits_{n=4}^{infty}frac{7n+5}{2^{4n-1}cdot n}=sumlimits_{n=1}^{infty}frac{7n+26}{2^{4n+11}cdot (n+3)}$. Общий член ряда: $u_n=frac{7n+26}{2^{4n+11}cdot (n+3)}$.
Частичная сумма ряда. Сходящиеся и расходящиеся ряды. Остаток ряда.
Пусть задан числовой ряд
$$
begin{equation}
sumlimits_{n=1}^{infty}u_n
end{equation}
$$
Сумма $S_n=u_1+u_2+ldots+u_n$ первых $n$ членов ряда называется n-й частичной суммой ряда (1). В сокращённом виде: $S_n=sumlimits_{k=1}^{n}u_k$.
Например, сумма первых пяти членов ряда (1) есть пятая частичная сумма ряда, т.е. $S_5$:
$$
S_5=u_1+u_2+u_3+u_4+u_5.
$$
Ряд $r_n=u_{n+1}+u_{n+2}+u_{n+3}+ldots$, полученный из ряда (1) отбрасыванием первых $n$ членов ряда, называется n-м остатком ряда (1). В сокращённом виде: $r_n=sumlimits_{k=n+1}^{infty}u_k$.
Например, если мы отбросим первые три члена ряда (1), то получим третий остаток $r_3$:
$$
r_3=u_4+u_5+u_6+ldots
$$
Теперь перейдём к понятию суммы ряда. Пусть $S_n$ – n-я частичная сумма ряда (1).
Если существует конечный предел $S=lim_{ntoinfty}S_n$, то его называют суммой ряда (1) и сам ряд именуют сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд называют расходящимся.
Вопрос вычисления суммы числового ряда рассмотрен в соответствующей теме.
Пример №4
Задан ряд $sumlimits_{n=1}^{infty}frac{4n+3}{2^n}$. Записать первую, вторую, третью и четвёртую частичную суммы. Указать первый, второй и третий остатки.
Решение
Нижний предел суммирования равен 1, поэтому под знаком суммы стоит общий член ряда: $u_n=frac{4n+3}{2^n}$.
Первая частичная сумма $S_1$ совпадает с первым членом ряда:
$$
S_1=u_1=frac{4cdot 1+3}{2^1}=frac{7}{2}.
$$
Вторая частичная сумма $S_2$ – это сумма первых двух членов ряда:
$$
S_2=u_1+u_2=frac{7}{2}+frac{11}{4}.
$$
Третья частичная сумма $S_3$ – это сумма первых трёх членов ряда:
$$
S_3=u_1+u_2+u_3=frac{7}{2}+frac{11}{4}+frac{15}{8}.
$$
Четвёртая частичная сумма $S_4$ – это сумма первых четырёх членов ряда:
$$
S_4=u_1+u_2+u_3+u_4=frac{7}{2}+frac{11}{4}+frac{15}{8}+frac{19}{16}.
$$
Естественно, что любую частичную сумму можно вычислить, просто сложив элементы. Например, $S_2=frac{7}{2}+frac{11}{4}=frac{25}{4}$.
Теперь перейдём к остаткам. Отбрасывая первый член, получим первый остаток ряда:
$$
r_1=u_2+u_3+u_4+u_5+ldots=frac{11}{4}+frac{15}{8}+frac{19}{16}+frac{23}{32}+ldots
$$
Отбрасывая первые два члена, запишем второй остаток ряда:
$$
r_2=u_3+u_4+u_5+ldots=frac{15}{8}+frac{19}{16}+frac{23}{32}+ldots
$$
Отбрасывая первые три члена, запишем третий остаток ряда:
$$
r_3=u_4+u_5+ldots=frac{19}{16}+frac{23}{32}+ldots
$$
В принципе, при желании остатки можно записать в сжатой форме:
$$
r_1=sumlimits_{n=2}^{infty}frac{4n+3}{2^n};; r_2=sumlimits_{n=3}^{infty}frac{4n+3}{2^n};; r_3=sumlimits_{n=4}^{infty}frac{4n+3}{2^n}.
$$
Ответ:
- Частичные суммы: $S_1=frac{7}{2}$, $S_2=frac{7}{2}+frac{11}{4}$, $S_3=frac{7}{2}+frac{11}{4}+frac{15}{8}$, $S_4=frac{7}{2}+frac{11}{4}+frac{15}{8}+frac{19}{16}$.
- Остатки: $r_1=frac{11}{4}+frac{15}{8}+frac{19}{16}+frac{23}{32}+ldots$, $r_2=frac{15}{8}+frac{19}{16}+frac{23}{32}+ldots$, $r_3=frac{19}{16}+frac{23}{32}+ldots$.
Некоторые свойства числовых рядов
- Ряд $sumlimits_{n=1}^{infty}u_n$ сходится тогда и только тогда, когда сходится любой из его остатков $r_n=sumlimits_{k=n+1}^{infty}u_k$. Отсюда следует, что отбрасывание или добавление к некоторому ряду конечного количества членов не изменяет сходимости ряда.
- Если ряд $sumlimits_{n=1}^{infty}u_n$ сходится и сумма его равна $S$, то любой его остаток $r_n$ стремится к нулю при $ntoinfty$, т.е. $lim_{ntoinfty}r_n=0$. Кроме того, верна формула $r_n=S-S_n$, где $S_n$ – n-я частичная сумма заданного ряда.
- Если ряд $sumlimits_{n=1}^{infty}u_n$ расходится и $Cneq 0$, то ряд $sumlimits_{n=1}^{infty}Cu_n$ также расходится.
- Если ряд $sumlimits_{n=1}^{infty}u_n$ сходится и сумма его равна $S$, то и ряд $sumlimits_{n=1}^{infty}Cu_n$ также сходится и сумма его равна $CS$ ($C$ – некоторая константа).
- Если ряды $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$ сходятся и суммы их равны соответственно $S_1$ и $S_2$, то и ряд $sumlimits_{n=1}^{infty}left(u_npm v_nright)$ также сходится и сумма его равна $S_1pm S_2$.
- Необходимое условие (признак) сходимости ряда: если ряд $sumlimits_{n=1}^{infty}u_n$ сходится, то $lim_{ntoinfty}u_n=0$.
- Достаточное условие (признак) расходимости ряда: если $lim_{ntoinfty}u_nneq 0$, то ряд $sumlimits_{n=1}^{infty}u_n$ расходится.
Исследовать на сходимость числовой ряд
Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ – это общий член ряда. $n$ – это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.
Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ – первый член прогрессии, а $q$ – основание. В данном случае сумма равна $S = frac{1}{1 – frac{1}{2}} = 2$.
Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.
Необходимый признак сходимости ряда
Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.
- Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
- Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится
ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.
| Пример 1 |
| Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$ |
| Решение |
| Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки. |
| Ответ |
| Ряд расходится |
| Пример 2 |
| Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$ |
| Решение |
| Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости. |
| Ответ |
| Требуется дополнительное исследование |
Признаки сравнения
Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.
- Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
- Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
- Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $
Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.
Признак сравнения
Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.
Предельный признак сравнения
Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.
ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.
| Пример 3 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$ |
| Решение |
|
Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$ Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится. |
| Ответ |
| Ряд сходится |
| Пример 4 |
| Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$ |
| Решение |
| Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно. |
| Ответ |
| Ряд сходится |
Признак Даламбера
Признак рекомендуется использовать, если в общем члене ряда есть:
- Число в степени. Например, $2^n, 3^{n+1}$
- Присутствует факториал. Например, $(n+1)!,(2n-3)!$
Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$
В зависимости от значения предела делается вывод о сходимости или расходимости ряда:
- При $0 le L le 1$ ряд сходится
- При $L > 1$ или $L = infty$ ряд расходится
- При $L = 1$ признак не даёт ответа и нужно пробовать другой
| Пример 5 |
| Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$ |
| Решение |
|
Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$ Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера. |
| Ответ |
| Числовой ряд сходится |
| Пример 6 |
| Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$ |
| Решение |
|
Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$ Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$ Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$ Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$ Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Ряд расходится |
Радикальный признак Коши
Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$
- Если $L<1$, то ряд сходится,
- если $L>1$, то ряд расходится,
- если $L=1$, то признак не даёт ответа о сходимости.
Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.
| Пример 7 |
| Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$ |
| Решение |
|
Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$ Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$ Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$ Делаем вывод: так как $L > 1$, то представленный ряд расходится. |
| Ответ |
| Ряд расходится |
| Пример 8 |
| Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$ |
| Решение |
|
Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$ Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$ Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится. |
| Ответ |
| Ряд сходится |