Как найти пьезометрический напор в сечении

2018-03-17

Как построить напорную и пьезометрическую линии

Напорная и пьезометрическая линии являются графической иллюстрацией уравнения Бернулли, они показывают изменение полного и статического напора вдоль потока.

Что такое напорная и пьезометрическая линии?

Пьезометрическая линия характеризует изменение удельной потенциальной энергии, на сужающихся участках понижается, на расширяющихся повышается, а на участках с постоянным сечением проходит горизонтально (если речь идет об идеальном движении без потерь энергии) или со снижением, вызванным гидравлическими потерями (если речь идет о вязкой жидкости). Пьезометрическая линия отображает изменение статического напора.

Напорная линия характеризует изменение суммарной удельной энергии, для идеального движения жидкости (без потерь энергии) проходит горизонтально, для вязкой жидкости снижается за счет гидравлических потерь.Напорная линия отображает изменение полного напора.

Напорную и пьезометрические линии, как правило, строят в координатной плоскости совмещенной с принципиальной схемой гидросистемы.

Пример построения напорной и пьезометрической линии

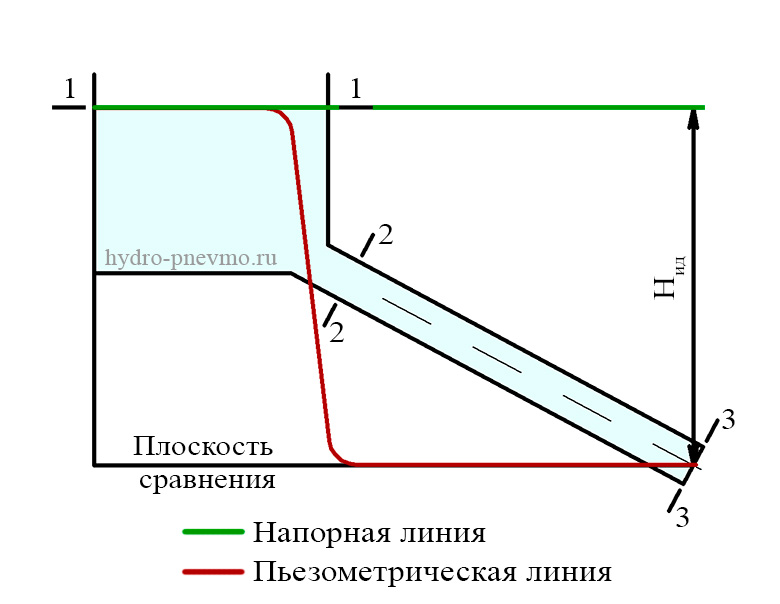
Рассмотрим систему, в которой жидкость вытекает из бака по наклонному трубопроводу, уровень в баке постоянный. Построим напорную и пьезометрическую линии для идеальной жидкости при отсутствии гидравлических потерь.

Плоскость сравнения проведем таким образом, чтобы она совпадала с нижней точкой оси трубопровода.

Для лучшего понимания построений выберем живые сечения 1-1, 2-2 и 3-3 на участках с плавно изменяющимися параметрами течения. Запишем уравнение Бернулли для этих сечений, учтивая, то, что потери энергии отсутствуют.

Н = z₁ + p₁/ρg + V₁²/2g = z₂ + p₂/ρg + V₂²/2g = z₃ + p₃/ρg + V₃²/2g

В баке полный напор равен геометрическому, при отсутствии гидравлических потерь, оттока и притока жидкости напор – величина постоянная, поэтому напорная линия будет горизонтальной.

---

---

Каждая точка пьезометрической линии находится непосредственным сложением геометрического (z) и пьезометрического (p/ρg ) напоров в выбранном сечении, либо вычитание из полного напора (Н) скоростного V²/2g .

В баке полный напор равен статическому, по этой причине напорная и пьезометрическая линии совпадают. В выходом сечении трубы статический напор отсутствует, т.к высота z = 0 и избыточное давление р = 0 (жидкость вытекает в атмосферу).

В промежуточном сечении трубы статический напор также будет равен 0, т.к полный напор величина постоянная, и скорость также будет постоянной (отток и приток жидкости отсутствуют, диаметр трубы постоянный). По этой причине на участке между сечениями 2-2 и 3-3 пьезометрическая линия совпадает с плоскостью сравнения. В зоне формирования скоростного напора происходит падение статического напора, поэтому пьезометрическая линия на этом участке устремляется вниз.

Напорная и пьезометрической линии для потока реальной вязкой жидкости

Построим напорную и пьезометрическую лини для другой системы, с учетом гидравлических потерь.

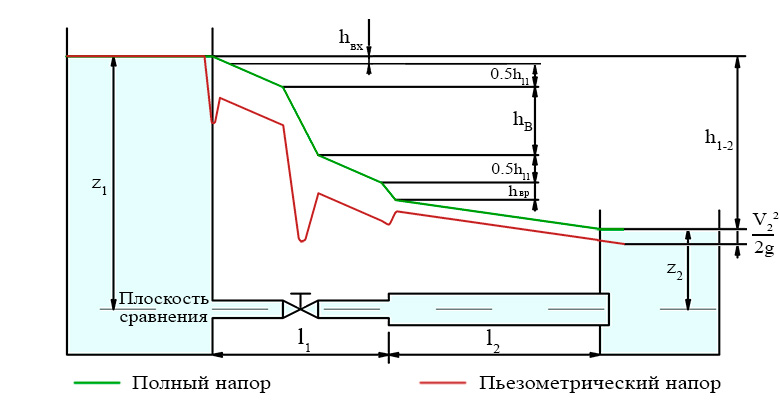
На рисунке обозначены:

• h_l1 – потери по длине на участке l1
• h_вх – потери удельной энергии на входе
• h_в – потери удельной энергии на вентиле
• h_вр – потери напора на местном сопротивлении – внезапном расширении
• h_1-2 – потери энергии на участке между живыми сечениями 1-2
• z – геометрическая высота
• V₂²/2g – скоростной напор

Снижение напорной линии вызвано потерями энергии на местных сопротивлениях, а также потерями по длине.

На участках с постоянным сечением снижение пьезометрической линии объясняется потерями по длине. При расширении трубопровода скорость движения жидкости падает, следовательно скоростной напор снижается, а статический возрастает, пьезометрическая линия на этом участке смещается вверх.

---

---

Выполнение
поставленной задачи осуществляется с
учётом следующих общих положений и
методик.

Рис.
9. Напор в точке трубопровода.

–так
называемый «свободный напор», значение
которого может быть регламентировано
согласно СНиП 2.04.02-98* и преимущественной
этажности застройки в населённом пункте.
Нормальный свободный напор принимаем
за минимальный.

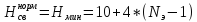(2.12)

где: 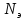– этажность здания.

Рис.
10. Падение пьезоотметки в трубопроводе.

(2.13)

(2.14)

(2.15)

Полагаем,
что минимальный пьезометрический напор
будет в самой удаленной точке 1 сети.
Отметка земли в этой точке равна 2м.
Следовательно, т.к. по заданию минимальный
напор в сети
.
отметка пьезометрической линии в этой
точке будет считать по формуле (2.13):

Далее
находим пьезометрические отметки для
каждой точки магистрали 4-1 по формуле
(2.13):

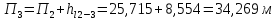
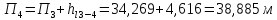
Найдя
пьезометрические отметки, можно вычислить
,
выразив из формулы (2.14):

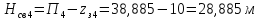
Для
расчета ответвления необходимо вычислить
допустимую потерю напора в ответвлении
и гидравлический уклон. Затем по таблицам
А. Ф. Шевелева [6] определить ближайший
меньший уклон по отношению к вычисленному
и соответствующий ему диаметр и скорость.

Фактический
свободный напор в конце ответвления не
должен быть меньше минимального.

Отметка
пьезометрической линии в начале
ответвления была получена при расчете
магистрали, а отметка в конце ответвления
будет равна отметке поверхности земли
в конце ответвления плюс заданный
свободный напор.

По
таблицам Ф. А. Шевелева и А. Ф. Шевелева
[6] определяем по расходу диаметр трубы
(по ГОСТу) наиболее экономичный для
данного участка, скорость и потерю
напора на 1000 м – 1000 i.

Потеря
напора на расчётном участке будет равна:

(2.16)

где: потеря напора на 1000м.

Ответвление
5-2:

По
таблице А. Ф. Шевелева [6] интерполяцией
находим для

и
или;V
= 0,6 м/с.

Ответвление
6-3:

.

По
таблице А. Ф. Шевелева [6] находим для

и
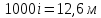или;V
= 1,02 м/с.

Ответвление
7-4:

По
таблице А. Ф. Шевелева [6] находим для

и
или;V
= 1,23 м/с.

Ответвление
8-7:

По
таблице А. Ф. Шевелева [6] интерполяцией
находим для

и
или;V
= 0,84 м/с.

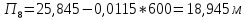
Ответвление
9-7:

По
таблице А. Ф. Шевелева [6] находим для

и
или;V
= 1,02 м/с.

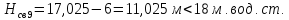
Полученные
результаты записываем в таблицу 4.

Таблица
4. Определение свободных напоров в
расчётных точках распределённой
водопроводной сети.

Номер расчётной точки					Исправленные значения
1	2	20		18	27,055	25,055
5,715
2	4			32,77	28,77
8,554
3	8	34,269		41,324	33,324
4,616
4	10	38,885		45,94	35,94
5 2	6		5,013		25,055	19,055
2
6 3	4		14,013		26,204	22,204
8
7 4	8,6		8,339		32,9	24,3
10
8 7	8		7,777		26	18
8,6
9 7	6		12,657		24,08	28,08
8,6

Из
таблицы видно, что пьезометрический
напор в точке 8 оказался меньше требуемого
(минимального). Диктующая точка выбрана
неправильно. Поэтому за диктующую точку
принимаем 8, имеющую наибольший недостающий
напор до минимального и введём в расчёт
поправку, увеличив все отметки
пьезометрической линии на величину
разности между величиной минимального
напора и напора в данной точке, т.е.
Запишем исправленные данные в 2 последние
колонки.

Значение
,
полученное после исправления, есть
искомое.

По
результатам расчётов оформляется рис.
11.

Соседние файлы в папке курсач docx283

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

11-я лекция.

11. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ

12.1. Простой трубопровод постоянного сечения.

12.1.1.Общий вид расчетного уравнения простого трубопровода

12.2.Простой трубопровод между двумя резервуарами.

12.3. Простой трубопровод при истечении в атмосферу.

12.4.Сифонный трубопровод. Вакуум на участке трубопровода.

12.5. Использование приблизительных зависимостей при расчете простого трубопровода.

Замена местных сопротивлений.

Рекомендуемые материалы

12.6. Три задачи на расчет простого трубопровода.

12.7 Графики напоров                                 

12.1. Простой трубопровод постоянного сечения

Трубопровод называют простым, если жидкость  транспортируется по нему от питателя к приемнику без ответвлений потока, но может иметь различные диаметры и включать местные сопротивления.

Трубопроводы, содержащие последовательные, параллельные соединения и  разветвления простых трубопроводов называются сложными.

Жидкость движется по трубопроводу за счет того, что  энергия, имеющаяся в начале трубопровода больше, чем в конце.

Энергии может быть обеспечена разностью уровней жидкости,  работой насоса или  давлением газа, например, за счет применения гидроаккумуляторов.

Движение жидкости за счет разности уровней (разности геометрических высот) применяется в гидротехнике и водоснабжении.

В машиностроении движение жидкости обеспечивается работой насоса и гидроаккумуляторами.  Гидроаккмуляторы –  емкости с разделителем  с одной стороны   использующие давление газа или пружины для создания запаса энергии  с другой стороны  рабочую жидкость, заправленную в гидроаккумулятор и находящуюся под действием давления газа.

На рис.12.1 изображен  простой трубопровод постоянного сечения расположенный произвольно в пространстве, состоящий из нескольких участков с  длиной l_i и диаметром d_i и содержащий местные сопротивления. 

 Запишем уравнение Бернулли для сечений «1 – 1» и “2-2”. Геометрические высоты: z₁ и z₂, избыточные давления: Р₁ и Р₂, скорости: V₁ и V₂.ρ

     (12.1)

Σh –   сумма потерь на трение по длине и в местных сопротивлениях, а также потерь на входе и выходе из трубопровода.

Гидростатическим напором называется сумма геометрического и пьзометрического напора в данном сечении трубопровода.

где z – геометрический напор,  – пьезометрический напор.

Разность гидростатических напоров в в сечениях 1 и 2, называется располагаемым напором – Н_расп, если величина гидростатического напора  Н_гст  для сечений 1 и 2 известна.

Если величина Н_гст не известна, разность гидростатических напоров называется потребным напором – Н_потр

и ее необходимо определить.

Таким образом,  разность может быть располагаемым или потребным напором,  в зависимости от наличия или отсутствия исходных данных.

, (12.2)

Используя разность гидростатических напоров из уравнения баланса напоров Бернулли, получаем  общий вид расчетного уравнения простого трубопровода

       ( 12.3 )

Это уравнение показывает, что имеющаяся в нашем распоряжении потенциальная энергиия в виде гидростатического напора затрачивается на преодоление разности скоростных напоров и потерь в местных сопротивлениях и на трение по длине.

Если площади питателя и приемника или длины трубопроводов велики по сравнению с  сечением трубопровода, тогда скоростными напорами можно пренебречь, уравнение простого трубопровода принимает вид

    (12.4)

В этом случае, потребный напор будет равен сумме сопротивлений в трубопроводе. Располагаемый напор  будет затрачиваться на преодоление  гидравлических сопротивлений.

Таким образом, уравнение простого трубопровода позволяет решить две задачи.

Первая: в случае известного располагаемого напора определить сопротивления, которые он может преодолеть.

Вторая: в случае известной суммы сопротивлений определить располагаемый напор.

Правая часть равенства (12.4) называется характеристикой трубопровода. Уравнение баланса напоров можно записать в виде

,        (12.4′)

где Σh – есть характеристика трубопровода, которая является степенной функцией расхода. Величина К – коэффициент  сопротивления трубопровода, а показатель степени m имеет значение, зависящее  от режима течения жидкости(ламинарный или турбулентный).

Используя формулу (12.4′) можно построить кривую потребного напора в координатах Н=f(Q), (рис.12.2), то есть зависимость напора от расхода жидкости в трубопроводе.

Величина Н_гст определяет положение характеристики трубопровода относительно начала координат Н-Q.

12.2.Простой трубопровод между двумя резервуарами.

Используем   уравнение располагаемого напора для расчета простого трубопровода, который соединяет два резервуара с постоянными уровнями жидкости и состоит из k последовательных участков длиной l_i и диаметром d_i, а также включает местные сопротивления.

Показанные на рис.12.3 уровни жидкости в резервуарах следует рассматривать, как пьезометрические уровни в питателе и в приемнике, поскольку геометрические напоры  в их сечениях равны z₁ = z₂, а за плоскость сравнения принята ось трубопровода.

Выражая потери на трение по длине и в местных сопротивлениях формулами

                 ,

получим уравнение простого трубопровода в виде:

            (12.5),

где λ _i и  ξ _i – коэффициент сопротивления трению и суммарный коэффициент местных сопротивлений на каждом участке, Vi – средняя скорость на каждом участке, Vk – скорость потока на выходе из трубопровода в резервуар,  α_kV²_k/2g – скоростной напор  при выходе из трубопровода в резервуар (потеря напора в выходном сечении трубопровода).  Коэффициент Кориолиса α_k = 1 – для турбулентного режима течения, α_k= 2 для ламинарного режима течения.

Используя уравнение неразрывности потоков

Q=V₁F₁ =…=V_iF_i=V_kF_{k     ,}

получим расчетное уравнение простого трубопровода в виде

,         ( 12.6 )

где F_k – площадь выходного сечения трубопровода с диаметром d_к, Fi – площадь трубопровода с диаметром di. 

Если трубопровод имеет длину l  и диаметр d,  при турбулентном режиме α_k = 1,  уравнение  упрощается

,   ( 12.7 )

где  Σξ – сумма коэффициентов потерь в местных сопротивлениях.

Из уравнения трубопровода  можно выразить скорость

 и расход ,

где  , μ – коэффициент расхода, а F – площадь сечения трубопровода.

Выражая скорость V = Q/F  через расход  и использовав значение ускорения свободного падения g = 9,81 м/с², получим  уравнение простого трубопровода в виде

         (12.8),

где l, d, H  в м, Q  в м³/с.

12.3. Простой трубопровод при истечении в атмосферу.

При истечении из резервуара в атмосферу (рис.12.3) уравнение Бернулли между сечениями 0-0 и 1-1 имеет вид

 (12.9)

где Н – располагаемый напор трубопровода, определяемый  высотой пьезометрического уровня,  – скоростной напор  в выходном сечении,  Σhп –  сумма потерь.

Так как потери напора при выходе в атмосферу  отсутствуют,  уравнение (12.9) при подстановке в него суммы потерь переходит в уравнение  (12.6),

поэтому уравнение (12.6 ) является общим  при истечении под уровень и в атмосферу.

12.4.Сифонный трубопровод. Вакуум на участке трубопровода.

Если часть длины трубопровода находится под вакуумом (например, сифонный трубопровод, область С,  рис.12.5),  необходимо проверить наибольший вакуум в опасном сечении С:

    (12.10)

где  h –  высота сечения С над начальным уровнем пьезометрическим уровнем в баке питателе; V – скорость в этом сечении; Σh_пС – сумма потерь напора на участке трубопровода до этого сечения. Для обеспечения нормальной бескавитационной работы трубопровода  должно выполняться условие

Р_вС < Рат – Рн.п.,

где РвС  –  вакуум в точке С, Рат – атмосферное давление,  Рн.п. – давление насыщенных паров жидкости при данной температуре.

12.5. Использование приблизительных зависимостей при расчете простого трубопровода. Замена местных сопротивлений.

При достаточно большой длине трубопровода можно пренебречь скоростным напором  V²/2g  по сравнению с потерями на трение по длине  и использовать для расчета приблизительные зависимости,  введя в них, если это необходимо замену коэффициентов   местных сопротивлений на потери по длине

.  

                ( 12.11 )

      (12.12)

При такой замене получаем

   (13.14)

Для трубопровода, состоящего только из k – последовательных участков труб с различными диаметрами di и длинами Li

                (12.15)

12.6 Определение коэффициентов трения

в зависимости от режима течения жидкости.

Расчет трубопроводов связан с выбором коэффициентов ξ местных сопротивлений и коэффициента трения λ.

1. Ламинарный режим.  При числе Рейнольдса равном Re ≤ 2300, коэффициент трения  определяется по формуле   λ=64/Re.

Для определения потерь используем формулу Дарси:

                     (12.17)

При подстановке  λ=64/Re потери на трение в трубопроводе

 (12.18)

Если скорость определить через расход V =Q/F = 4Q/(πd²)

  (12.19)

2.Турбулентный режим Re > 2300.

А.Область гидравлически гладких труб.

При числах Рейнольдса   Re_гл ≤ 20d/Δэ,  здесь  Δэ –эквивалентная абсолютная шероховатость,  коэффициент сопротивления трению определяется  по формуле Канакова

   (12.20)

или  по формуле Блазуиса

                                                          (12.21)

Подставляя формулу Блазиуcа в формулу Дарси  

   (12.22)

Зависимость  λ от Re для гидравлически гладких труб дана   в справочниках  или ее можно взять в задачнике на стр.228.

К этой области относятся технически гладкие трубы , цельнотянутые из цветных металлов, во всем диапазоне их практического применения по числам Re, а также стальные трубы  до чисел Re ориентировочно равных Re_гл ≥ 20d/Δ.

Б. Переходная зона.

При числах Рейнольдса  20d/Δ ≤Re ≤ 500 d/Δ в переходной области λ зависит  и от числа Re и от относительной гладкости.

Значения λ в функции Re и относительной гладкости d/Δ  по данным теплотехнического института, приведены в справочниках в виде графика Мурина в задачнике.

Можно применять для определения коэффициента  λ формулу Альтшуля.

      (12.23)

Средние значения эквивалентной шероховатости для новых труб Δ =0,1мм, для бывших в употреблении  Δ = 0,2 мм.

В. Область гидравлически шероховатых труб.

При  числах Рейнольдса Re ≥ 500 d/Δ  коэффициент λ зависит только от шероховатости.   Для определения значений коэффициента λ можно использовать формулу Никурадзе

     (12.24 )

Или формулу Шифринсона

   ( 12.24 )

Для старых стальных и чугунных труб,  эквивалентная шероховатость до Δ = 1 мм, применимо выражение, где d  в м

   ( 12.24 )

Зависимость λ  от d/Δ для квадратичной области дается по таблицам, пример такой таблицы приведен в задачнике на стр.229.

12.6. Три задачи на расчет простого трубопровода.

Задача 1. Даны: расход жидкости Q, кинематическая вязкость жидкости ν, размеры трубопровода l, d шероховатость стенок – Δ.

Найти требуемый напор – Н

1.По известным Q,  d, ν находится число Рейнольдса –  Re  и определяется режим движения.

1.1  При ламинарном режиме, напор определяется по ф-ле

   (12.25),

где L = l + Σl_э – приведенная длина трубопровода, эквивалентные длины lэ  местных сопротивлений при ламинарном режиме в трубопроводе существенно зависят от  числа Рейнольдса: lэ/d = f(Re) .

1.2.При турбулентном режиме Н определяется по формулам:

  –  короткий трубопровод или

  – длинный трубопровод с преобладающими потерями на трение, в котором по известным Re, d и Δ выбирают λ,  ξ и lэ, которые позднее войдут в  L = l + Σl_э.

Задача 2. Даны: располагаемый напор – Н, размеры трубопровода: l, d, Δ – шероховатость свойства жидкости. Найти расход – Q.

Задача 3. Даны располагаемый напор – Q, длина трубопровода l, шероховатость стенок – Δ. Найти диаметр трубопровода – d.

Из уравнения располагаемого напора определяются искомые величины

12.7 Построение диаграмм напоров в трубопроводе

Последовательность  построения диаграмм.

1. Выделение в трубопроводе участков, на которых происходит изменение сечения и  участки с местными сопротивлениями.

2. Начало первого участка определяет начало трубопровода, а величину напора – напор в  питателе.

Если начало трубопровода связано с потерями, как например, при входе в трубу, начало участка немного смещают влево, чтобы показать качественный участок сжатия струи.

3. Первый участок –  вход в трубопровод, в котором происходит сужение потока и  увеличение скорости до значения .  В конце первого участка от располагаемого напора откладываем потери в данном местном сопротивлении (в сужении) –    , а от  величины h_м.п. откладываем  величину скоростного напора в конце участка. В конце первого участке величина располагаемого напора равна:

Потери, связанные с деформацией потока, входят в величину .

График напоров, построение которого дано на рис.12.8 показывает изменение по длине трубопровода полного напора потока и его составляющих.

4. Линия напора (удельной механической энергии потока ) строится путем последовательного вычитания  потерь, нарастающих вдоль потока  из начального напора потока (заданного пьезометрическим уровнем в питающем резервуаре).

Там, где имеется  местная деформация потока и ход изменения напоров может быть показан только качественно, линии напоров даны штриховой линией).

Построение графика напоров для вертикального трубопровода  дано на рис. 12.10.

1. Напоры в каждом сечении откладываются по горизонтали таким образом, чтобы ось трубы являлась началом отсчета пьезометрических напоров. 

2.Графики напоров, показывают изменение по длине трубопровода полного напора потока и его составляющих.

Бесплатная лекция: “3. Свойства Z-преобразования” также доступна.

3. Из начального напора потока (заданного пьезометрическим уровнем в питающем резервуаре) вычитаются  потери, нарастающие вдоль трубопровода, таким образом, потеря в конце участка формирует (пьезометрический) уровень напора на следующий участок.

4. Пьезометрическая линия (линия изменения гидростатического напора потока) строится путем вычитания скоростного напора  в каждом сечении полного напора потока. 

Пьезометрический напор  Pи/(ρg)    в каждом сечении (Ри – избыточное давление)  определяется на графике вертикальным расстоянием от  центра  сечения до  пьезометрической линиии;

Скоростной напор  -вертикальное расстояние между пьезометрической линией и линией напора. На участках местной деформации потока, где ход изменения напоров может быть показан только качественно, линии напоров даны штриховой линией.

График напора для длинного трубопровода строится упрощенно (рис.12.11), поскольку малость скоростных напоров позволяет рассматривать линию напора и пьезометрическую линию, как совпадающие.