Как найти ph бензойной кислоты

Для слабых кислот:
рН = 1/2 (pKa + pCa).

pKa = – lg Ka,
Ka – константа кислотности – константа диссоциации слабой кислоты.

pCa = – lg Cа,
Са – молярная концентрация кислоты.

Могу проверить Ваш расчёт.
.

перекрываться кривыми, рассчитанными из уравнения третьей степени. Уравнение (3.16), таким образом, может быть применимо только к сильным и очень слабым кислотам умеренных концентраций. Напротив, уравнение (3.23) (табл.3.1) применимо почти всегда и может давать отклонения только в области экстремально малых значений концентраций. Уравнение (3.23) перекрывает область действительных значений уравнения (3.16) и при Кa2/4 << КaС0 переходит в него. Уравнение (3.9) охватывает области применимости уравнений (3.16) и (3.23). При КwКa <СH+3 и КbС0 >>Кw оно переходит в уравнение (3.23,

табл.3.1).

С помощью диаграммы lgC-pH можно также определить концентрационные соотношения в растворе двух слабых кислот, например, иона аммония и уксусной кислоты (рис.3.4).

На диаграмме различают три области значений рН: рН< рКа1; рКа1 < рН<рКа2; рН>рКа2. В первой области обе кислоты NH4+ и CН3СООН находятся в недиссоциированном состоянии.

Рис.3.4. Логарифмическая рН-диаграмма для раствора 0.1М по уксусной кислоте и 0.1 М по NH4+

Таблица 3.1

Формулы для расчета рН растворов слабых кислот

Во второй области в основном существует более слабая кислота NH4+, а также более слабое основание СН3СОО−, а в третьей области почти исключительно находятся основания NH3 и CH3СОО−.

Отсюда ясно, что при кислотно-основном титровании смеси двух слабых кислот происходит их последовательная депротонизация: вначале более сильной кислоты, а затем более слабой. Интересна точка Р. Для нее справедливо условие С(NH4+) ≈ C(СН3СОО−), которое выполняется и для раствора ацетата аммония, так что абсцисса точки Р соответствует значению рН этого раствора. Из рис.3.4 можно вывести выражение для точки Р, пригодное для расчета рН растворов солей, образованных анионами слабой кислоты и катионами слабого основания:

рН = (1/2) (рКa1 + рКa2 ) (3.24)

Оно показывает, что рН такого раствора определяется только значениями констант диссоциации обеих кислот и не зависит от концентрации.

Уравнение (3.24) можно упростить введением в него константы автопротолиза воды:

Данное уравнение показывает, что если кислота 1 сильнее основания 2, то раствор соли, образованной катионом этого основания и анионом этой кислоты, имеет кислую реакцию; если же основание 2 сильнее кислоты 1, то раствор соли дает щелочную реакцию.

Уравнения (3.24) и (3.25) действительны, если выполняются неравенства СН+<<СА– и СОН-<< СНА , и недействительны для кислот или оснований, сила которых превышает определенное значение.

III.2.1. Математическое описание логарифмических рН-диаграмм

Кривые, приведенные на диаграмме lgC – pH, построены на основании уравнений, в которых концентрации СНА и СА– являются

функцией рН. Эти зависимости выведены комбинированием уравнений (3.4), (3.5), (3.6) и (3.7). При решении их относительно СНА и затем относительно СА– получают следующие уравнения:

При графическом изображении этих зависимостей на диаграмме lgC0 –

находится выше линии нейтральности, причем чем слабее кислота, тем асимметричнее кривая титрования или тем величина рТ > 7.

Рис.3.5. Кривые титрования 0.1 н. растворов кислот с различными значениями констант кислотности 0.1 н. раствором сильного основания

3. На кривых титрования слабых кислот в точке полунейтрализации (т.е. при степени оттитровывания r = 0.5) рН = рК.

То же самое можно вывести из выражения для закона действующих масс после решения уравнения относительно СН+ и логарифмирования:

При добавлении половины стехиометрического количества раствора основания, т.е. при r = 0.5, с достаточным приближением можно считать СA– = СHA и тогда получим lg(СA-/СHA) = 0. При этом уравнение

(3.42) превращается в (рН1/2 = рКa), где рН1/2 – это рН при r = 0.5. Возрастающий полого участок кривой, в середине которого на-

ходится рН1/2, характеризуется тем, что даже при добавлении относительно больших количеств титранта – основания – значение рН изменяется незначительно. Такое поведение называется буферным действием, а соответствующий раствор – буферным раствором. В нашем случае буферная смесь состоит из слабой уксусной кислоты и ацетата натрия.

4. Так называемый показатель титрования рТ, т.е. рН в точке эквивалентности, как отмечалось чуть раньше, тем дальше сдвинут в основную область, чем слабее титруемая кислота. При этом скачок рН в области точки эквивалентности увеличивается с увеличением силы

109

титруемой кислоты. Это явление имеет большое практическое значение: чем меньше скачок титрования, тем менее круто восходит кривая титрования в области точки эквивалентности и тем менее точно можно определить точку перегиба и объем титранта в точке эквивиалентности. Поскольку точку эквивалентности при титровании определяют непосредственно по абсциссе точки перегиба на кривой титрования, результаты титрования в целом тем менее точны, чем слабее титруемая кислота. Очень слабые кислоты с константами диссоциации Кдисс < 10−9 не титруются в водных средах. Показатель титрования слабой кислоты можно определить из диаграммы lgC – pH (точка Р5 на рис.3.3) или из кривой сопряженного с кислотой основания, представленной на рис.3.2.

Рис.3.6. Кривые титрования сильных и слабой кислот различной концентрации сильным основанием

Пример. Сопряженное с 0.1н кислотой, рКа которой равно 8, такой же концентрации (0.1н.) основание имеет рКb = 6, так как рКa + рКb = 14, и соответствующее ему значение рН равно 10.5 (рис.3.2).

На рис.3.6 показано влияние исходной концентрации титруемой кислоты на ход кривой титрования слабой или соответственно сильной кислоты. Из рис.3.6 можно сделать следующие выводы:

а) Скачок рН в области точки эквивалентности при титровании сильной кислоты тем меньше, чем меньше исходная концентрация кислоты.

б) Ход кривых титрования слабых кислот в области 0 < r < 1 в меньшей степени зависит от исходной концентрации кислот, чем ход кривых титрования сильных кислот. Кривые титрования слабых кислот

110

проходят (за исключением кривых для концентраций С0 < Ка) через точку, в которой r = 0.5, рН =рКа.

III.3.2. Связь между диаграммами lgC-pH и кривыми титрования

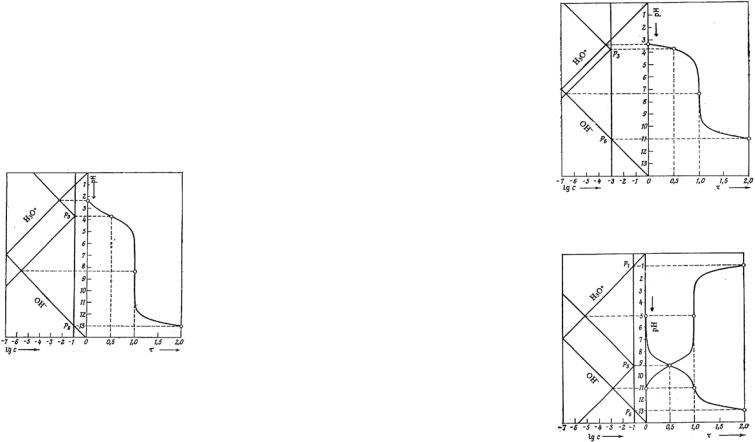
Логарифмическая диаграмма особенно упрощает построение кривой титрования, как это видно из рис.3.7 на примере титрования слабой кислоты раствором сильного основания. На рис.3.8 и 3.9 представлены другие типы диаграмм – для особенно низких исходных концентраций и для очень слабых кислот, соответственно.

Рис.3.7. Логарифмическая рН-диаграмма и кривая титрования для 0.1 н. раствора муравьиной кислоты сильным основанием

Такие комбинированные диаграммы дают возможность получать дополнительную информацию из диаграмм lgC−pH. На рис.3.9 приведена комбинированная диаграмма кислотно-основной пары NH4+/NH3 при концентрации 0.1 моль/дм3.

Из формы обеих кривых ясно, что титрование аммиака соляной кислотой характеризуется большей точностью, чем титрование хлорида аммония раствором едкого натра. Так, длина отрезка Р3Р6 (рис.3.8) является достаточно точной мерой скачка рН при титровании кислоты раствором сильного основания, а длина отрезка Р3Р1 дает величине скачка при титровании сопряженного основания раствором сильной кислоты.

Рис.3.8. Логарифмическая рН-диаграмма и кривая титрования для 0.001 н. раствора муравьиной кислоты сильным основанием

Рис.3.9. Логарифмическая рН-диаграмма и кривая титрования для 0.1 н. раствора NH4Сl или раствора NH3 cоответственно

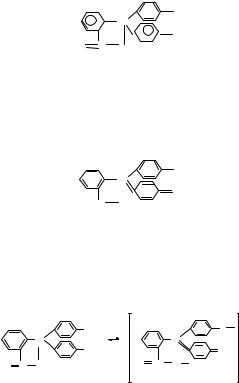
Из диаграммы lgC-pH можно также построить кривую дифференцированного титрования кислот в их смеси. На рис.3.10 приведена диаграмма для раствора, содержащего смесь соляной (хлороводородной) и уксусной кислот с концентрацией каждой 0.1 моль/дм3, а на рис.3.11 – диаграмма для раствора смеси двух слабых кислот с рКа1 = 3.15 и рКа2 = 6.9.

Рис.3.10. Логарифмическая рН-диаграмма и кривая титрования для смеси хлористоводородной и уксусной кислот (С0 = 0.1 моль/ дм3). Титрант – сильное основание (С = 0.1 моль/ дм3)

Рис.3.11. Логарифмическая рН-диаграмма и кривая титрования для раствора двух кислот с рКа1 = 3.15 и рКа2 = 6.9 (С0 = 0.1 моль/дм3)

Из рис.3.11 ясно, что кислоты в их смеси можно оттитровать дифференцированно с достаточной точностью, если значения рКа отличаются по меньшей мере на 3 единицы.

На рис.3.12 приведена комбинированная диаграмма для фосфорной кислоты H3РО4. При титровании H3РО4 проявляет свойства двухосновной кислоты, поскольку третья константа диссоциации (рКа3 = 12.66) настолько смещена в основную область, что по третьей ступе-

113

ни кислоту нельзя оттитровать обычным путем (т.е. прямым титрованием).

Рис.3.12. Логарифмическая рН-диаграмма и кривая титрования для фосфорной кислоты (рКа1 = 2.2, рКа2 = 7.2 и рКа3 = 12.66; С0 = 0.1 моль/дм3). Титрант – сильное основание

III.4. Кислотно-основные индикаторы

III.4.1. Теории индикаторов

Как отмечалось несколько ранее, для возможно точного определения количества вещества (кислоты, основания, различных солей) в анализируемой пробе (в навеске или в данном объеме) при кислотноосновном титровании необходимо, чтобы в момент эквивалентности (в точке эквивалентности) окраска раствора изменилась. Этого можно достичь при применении кислотно-основных индикаторов, изменяющих свою окраску при рН в конечной точке титрования.

Индикаторы, применяемые в методе нейтрализации, представляют собой органические вещества достаточно сложного строения, принадлежащие к различным классам органических соединений. Все кислотно-основные индикаторы обладают одним общим свойством – они изменяют свою окраску в зависимости от изменения рН раствора.

III.4.1.1. Теория индикаторов Оствальда

Эта теория называется ионной теорией индикаторов.

114

2) Каждый индикатор существует в двух формах (А и В), которые находятся в равновесии друг с другом и могут переходить одна в другую:

HInd ↔ HInd

A B

Формы А и В имеют различное строение и потому имеют различную окраску. Эти формы называются таутомерными (говорят, что обе формулы представляют одно и то же химическое соединение в различных таутомерных формах).

3) Различные таутомерные формы индикаторов имеют различную окраску индикаторов, меняющуюся при действии кислот и оснований. Это можно объяснить тем, что форма А индикатора не может диссоциировать, а 2 форма (В) индикатора может диссоциировать с образованием ионов Н+ и Ind−:

(HInd)A ↔ (HInd)B ↔ H+ + Ind−

Применив закон действующих масс (ЗДМ) к диссоциации формы В, можно записать:

K(Hind)B = [H+[·[Ind−]/[HInd]B

Но между двумя формами существует равновесие, которое подчиняется ЗДМ:

[HInd]B/[Hind]A = Kтаут

В большинстве случаев индикатор находится в форме А, а количество формы В – мало и его окраска незаметна. При добавлении щелочи (ОН−-ионов) концентрация [H+] понижается и усиливается диссоциация [HInd]B для постоянства KHind, в результате этого уменьшается концентрация [HInd]B.

III.4.1.3. Ионно-хромофорная теория индикаторов

Согласно дополняющим друг друга ионной и хромофорной теориям в растворах кислотно-основных индикаторов одновременно имеют место равновесия, обусловленные диссоциацией молекул и равновесия, связанные с внутримолекулярными перегруппировками одних форм индикатора в другие, отличающиеся различным строением. Поэтому обе рассмотренные теории объединены в одну общую ионнохромофорную теорию индикаторов.

Рассмотрим наиболее часто применяемые индикаторы кислотноосновного титрования, переход их окраски.

1. Фенолфталеин. Данный индикатор представляет собой бесцветное кристаллическое, нерастворимое в воде, но хорошо растворимое в спирте вещество. Поэтому в химических лабораториях применя-

ют 0.1% раствор индикатора в 50% этиловом спирте. В нейтральной и кислой среде фенолфталеин находится в так называемой лактонной форме, не имеющей окраски и имеет следующую структурную формулу:

OН

C

OН

O C O

бесцветная форма фенолфталеина

При действии на фенолфталеин разбавленных растворов щелочи, например NaOH, образуется двунатриевая соль, имеющая хиноидное строение, имеющая характерное окрашивание, присущее данному хромофору и окрашенное в красный цвет:

ONa

C

O

O C O Na

окрашенная форма фенолфталеина

В результате реакции происходит внутримолекулярная перегруппировка, показанная на нижеприведенной схеме:

Бесцветная лактонная форма Окрашенная хиноидная форма

или в более общей форме:

фН + NaOH ↔ фNa + H2O

Хиноидная группа присутствует и в нейтральной, и в кислой среде, но в малых количествах, не превышающих 10%. Эти структурные изменения фенолфталеина (бесцветная лактонная форма – окрашенная хиноидная форма) наблюдаются при значениях рН = 8…10. Но при дальнейшем увеличении рН раствора (при добавлении избытка щелочи, рН = 13…14) фенолфталеин претерпевает новую структурную перегруппировку. При этом образуется тризамещенная натриевая соль, не имеющая хиноидного строения:

OH

ONa

C

ONa

O C ONa

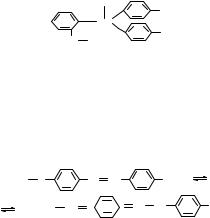
2. Метиловый оранжевый (гелиантин, натриевая соль N- диметиламинобензолсульфокислоты) – один из наиболее часто используемых в химических лабораториях индикатор, представляет собой растворимый в воде оранжево-желтый порошок. В химической лаборатории обычно применяется 0.05% водный раствор. Имеет следующую структурную формулу:

Отметим, что в верхней части (в нейтральной и щелочной среде) окраска индикатора в азоформе – желтая, в то время как при рН < 3.1 (нижняя часть структурной формулы) индикатор принимает хиноидную форму, окрашенную в красный цвет.

В первом случае при рН > 4.4 в молекуле индикатора метиловый оранжевый хромофорной группой является азогруппа –N=N−, которой свойственна желтая окраска, и ауксохромная сульфогруппа −SO3H, углубляющая окраску раствора.

При добавлении к раствору с индикатором кислоты (при уменьшении рН <3.1) происходит изменение структуры молекулы индикатора – в молекуле появляется хиноидная группа

3. Метиловый красный. Молекула метилового красного по своей структуре в кислой и щелочной средах практически ничем не отличается от молекулы метилового оранжевого. Они имеют лишь различные ауксохромные группы. Так, у метилового красного ауксохромной группой является −COONa. Добавим лишь, что введение ауксохромной группы −COONa в молекулу метилового красного приводит к смещению интервала перехода окраски индикатора в более основную область рН (до рН = 4.4 и более кислом растворе индикатор имеет красную окраску, а при рН, превышающих 6.2, раствор с индикатором метиловый красный принимает желтую окраску), так как заместитель СОО− является менее кислым, чем сульфогруппа SO32−.

Как отмечалось ранее, кислотно-основные индикаторы (рНиндикаторы) обычно представляют собой слабые органические кислоты или основания, окраска ионной и молекулярной форм которых раз-

лична. Если ионная и молекулярная формы абсорбируют свет в видимой области спектра, такие индикаторы называются двухцветными. Если только одна форма индикатора поглощает свет в видимой области спектра, то такой индикатор называют одноцветным (например, фе-

нолфталеин).

Двухцветные индикаторы. Реакцию нейтрализации индикатора, являющегося кислотой, можно представить следующим образом:

молекулярная ионная форма форма

Логарифмическое выражение закона действующих масс для этой реакции:

где KHInd – константа диссоциации индикатора HInd; CHInd, fHInd, СInd–, fInd– – концентрация и коэффициент активности молекулярной и ионной

форм индикатора.

В разбавленном растворе принимают fHInd ≈ fInd–. Тогда каждому значению рН соответствует определенное соотношение СHInd/СInd–.

Если принять, что растворы с одинаковой концентрацией HInd и Ind– имеют одинаковую интенсивность окраски, которая пропорциональна концентрации, следует ожидать, что в пределах относительно большой области рН окраска ионной формы индикатора непрерывно переходит в окраску недиссоциированной молекулярной формы.

При этом было бы невозможно определить значение рН, так как нет резкого изменения окраски. Однако здесь сказывается невысокая чувствительность зрения человека: глаз до тех пор воспринимает, как было установлено ранее, окраску как чистую, пока содержание второго компонента в 10 раз не превысит содержание первого.

Чистую окраску второго компонента можно видеть, если ее интенсивность примерно в 10 раз больше, чем интенсивность окраски первого.

При переходе из кислой в щелочную область значение рН, при котором происходит первое видимое изменение окраски индикаторакислоты, можно определить на основании уравнения (3.41) по формуле

(рН)1 = рКHInd − lg10 = pKHInd − 1 (3.45)

При дальнейшем увеличении рН чистая окраска анионов индикатора возникает при