Как найти пирамиду с цифрами

Ответ.

А теперь давайте подробно разберем данное задание.

Рассмотрим следующую ячейку в пирамиде.

Нам известно, что 11 — это сумма 7 и еще одного неизвестного числа. Очевидно, что второе число это 4, таким образом можем заполнить ячейку справа в первом ряду.

Далее найдем число, которое нужно записать во второй ряд пирамиды. Это должно быть число, сложив которое с 11, получилось бы 23. Это число 23 — 11 =  12. Запишем его в пирамиду.

В пирамиде осталось одна пустая ячейка. В ней должно быть число, прибавив к которому 7 должно получиться 12. Т.о. в пустой ячейке слева в первом ряду должно быть число 5.

Далее перейдем ко второй пирамиде.

Рассмотрим ячейки во втором ряду. Там должны два числа в сумма которых должна быть равна 24. При этом, заметим, что чтобы получить искомые два числа во втором столбце, нужно к какому-то неизвестному числу, которое располагается в средней ячейке первого ряда прибавить 3 и 5, то есть разность этих двух чисел должна равняться 2. Под эти условия подходит числа 11 и 13, ведь 11 + 13 = 24, а с другой стороны 13 — 11 = 2. Таким образом, можем заполнить ячейки 2 ряда.

И осталось найди последнее число в первом ряду. Это число можно получить, если его прибавить к 3 и получим тогда 11. Таким образом. это число 8.

Рассмотрим еще несколько числовых пирамид.

Числовые пирамиды — 2 класс

Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.

Заполним пропуске в каждой пирамиде и получим следующие.

Числовые пирамиды — 3 класс

Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.

Заполним пропуске в каждой пирамиде и получим следующие.

Числовые пирамиды — 4 класс

Два числа сложили и записали суммы над ними. Заполни пропуски в пирамидах.

Заполним пропуске в каждой пирамиде и получим следующие.

Сразу же понятно, что число справа 20 равно 38 – 20 = 18. Вставляю его:

Теперь надо найти число между 3 и 5. Я его принимаю за “х”: составляю уравнение:

х + 3 + х + 5 = 20. Вычисляю:

2х = 20 – 8 = 12.

х = 6. Вставляю 6 в пирамиду, и тут же понимаю, что под 20 стоит 3 + 6 = 9. Вставляю и его:

Дальше пошло легче:

5 + 6 = 11, вставляю над шесть и пять, слева от 9.

18 – 11 = 7. Ставлю 7 под 18, слева от 11.

осталось последнее число в правом нижнем углу:

7 – 5 = 2.

Пирамида готова.

Следующая пирамида очень лёгкая:

Всё ясно из картинки:

14 – 9 = 5.

5 – 2 = 3.

9 – 3 = 6.

Я рисую красным, чтобы отличались.

Здесь тоже не сложно. Вставляю 4 и 13:

12 – 8 = 4.

21 – 8 = 13.

А дальше ещё проще. Начинаю с нижнего ряда:

13 – 8 = 5.

8 – 5 = 3.

Поднимаюсь выше:

13 + 12 = 25.

И самая верхняя:

21 + 25 = 46.

Последний треугольник с подсказкой. Только вместо “х” используют “а”. Пусть так. Составляю уравнение:

10 + а + 8 + а = 32. Вычисляю:

2а = 14. а = 14/2 = 7.

Подставляю числа в пирамиду:

Теперь, наверное, без вычислений понятно. Ставлю 7-ку. Внизу нахожу вычитанием, а вверху сложением.

В этом выпуске рассмотрим классическую задачу, известную под названием «Золотая гора». На CheckiO её реализовали в этой задаче.

Представьте себе треугольник, составленный из чисел. Одно число расположено в вершине. Ниже размещено два числа, затем три, и так до нижней грани. Вы начинаете на вершине, и нужно спуститься к основанию треугольника. За каждый ход вы можете спуститься на один уровень и выбрать между двумя числами под текущей позицией. По ходу движения вы «собираете» и суммируете числа, которые проходите. Ваша цель — найти максимальную сумму, которую можно получить из различных маршрутов.

Рассмотрим различные методы решения.

Рекурсия

Первым делом в голову приходит мысль использовать рекурсию и просчитать все пути от вершины. Когда мы спускаемся на один уровень, то все доступные числа ниже образуют новый меньший треугольник, и можно запустить нашу функцию уже для нового подмножества и так пока не достигнем основания.

def golden_pyramid(triangle, row=0, column=0, total=0):
    global count
    count += 1
    if row == len(triangle) - 1:
        return total + triangle[row][column]
    return max(golden_pyramid(triangle, row + 1, column, total + triangle[row][column]),
               golden_pyramid(triangle, row + 1, column + 1, total + triangle[row][column]))

Как мы видим, на первом уровне мы запустим нашу функцию два раза, затем 4, 8, 16 раз и так далее. В итоге мы получим сложность алгоритма 2^N и, например, для 100-уровневой пирамиды нам нужно будет уже где-то ≈10³⁰ вызовов функции. Многовато.

Динамическое программирование

Что если попробовать использовать принцип динамического программирования и разбить нашу проблему на множество мелких подзадач, результаты которых мы затем аккумулируем. Попробуйте взглянуть на треугольник вверх ногами. А теперь на второй уровень (то есть предпоследний от основания). Для каждой ячейки мы можем решить, каким будет лучший выбор в наших маленьких трёхэлементных треугольничках. Выбираем лучший, суммируем с рассматриваемой ячейкой и записываем результат. Таким образом, мы получили наш треугольник, но на один уровень ниже. Повторяем данную операцию снова и снова. В результате нам нужно (N-1)+(N-2)+…2+1 операций и сложность алгоритма равна N².

def golden_pyramid_d(triangle):
    tr = [row[:] for row in triangle]  # copy
    for i in range(len(tr) - 2, -1, -1):
        for j in range(i + 1):
            tr[i][j] += max(tr[i + 1][j], tr[i + 1][j + 1])
    return tr[0][0]

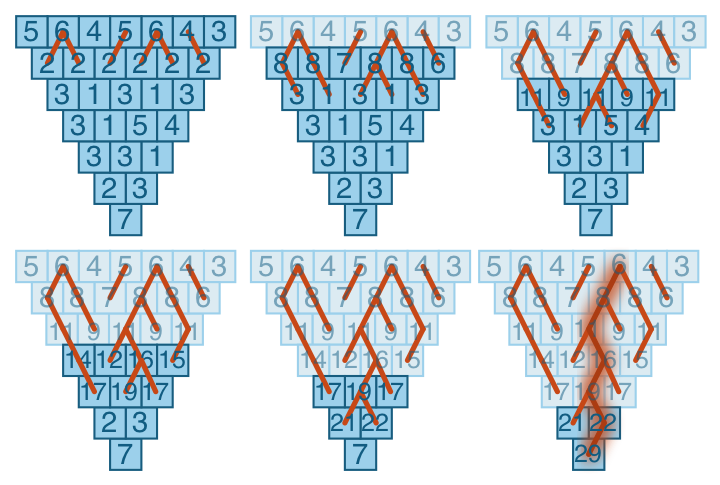
Решения игроков CheckiO

Пользователь gyahun_dash написал интересную реализацию описанного выше метода ДП в своем решении «DP». Он использовал reduce, чтобы проходить по парам строк, и map чтобы обработать каждую из них.

from functools import reduce

def sum_triangle(top, left, right):
    return top + max(left, right)

def integrate(lowerline, upperline):
    return list(map(sum_triangle, upperline, lowerline, lowerline[1:]))

def count_gold(pyramid):
    return reduce(integrate, reversed(pyramid)).pop()

Игрок evoynov использовал двоичные числа, чтобы перебрать все возможные маршруты, представленные как последовательность 1 и 0 в своем решении «Binaries». И это наглядный пример сложности алгоритма с рекурсией и перебором всех маршрутов.

def count_gold(p):
    path = 1 << len(p)     res = 0     while bin(path).count("1") != len(p) + 1:         s = ind = 0         for row in range(len(p)):             ind += 1 if row > 0 and bin(path)[3:][row] == "1" else 0
            s += p[row][ind]
        res = max(res, s)
        path += 1
    return res

И чтобы не было скучно, посмотрим на легкий мозгодробитель от пользователя nickie и его однострочник «Functional DP», который только формально состоит из двух строк. Конечно, это решение из категории «Творческих» («Creative»). Не думаю, что автор использует такое на боевом коде. А просто для так для веселья, почему бы и нет.

ount_gold=lambda p:__import__("functools").reduce(lambda D,r:[x+max(D[j],D[j+1])
for j,x in enumerate(r)],p[-2::-1],list(p[-1]))[0]

Вот и всё на сегодня. Делитесь вашими идеями и мыслями.

Спасибо CheckiO за интересную задачу.