Построение треугольника по трем элементам
Вы будете перенаправлены на Автор24
Задачи на построение
В геометрии довольно распространены так называемые задачи на построение. Их суть заключается в том, чтобы построить какой-либо геометрический объект по какому-либо достаточному набору начальных условий имея под рукой только циркуль и линейку. Рассмотрим общую схему для выполнения таких задач:
Анализ задачи.
В эту часть входит установление связи между элементами, которые необходимо построить и начальными условиями задачи. После выполнения этого пункта у нас должен появиться план по решению нашей задачи.
Построение.
Здесь мы выполняем построения по плану, который был нами составлен выше.
Доказательство.
Здесь мы доказываем то, что построенная нами фигура действительно удовлетворяет начальным условиям задачи.
Исследование.
Здесь мы выясняем, при каких данных задача имеет одно решение, при каких несколько, а при каких ни одного.
Далее будем рассматривать задачи на построение треугольников по различным трем элементам. Здесь мы не будем рассматривать элементарные построения, таких как отрезок, угол и т.д. К этому моменту эти навыки уже у Вас должны иметься.
Построение треугольника по двум сторонами и углу между ними
Постройте треугольник, если нам даны две стороны и угол, который находится между этими сторонами.
Пусть нам даны отрезки $AB$ и $AC$ и угол $α$. Нам нужно построить треугольник $ABC$ с углом $C$ равным $α$.
Составим план построения:
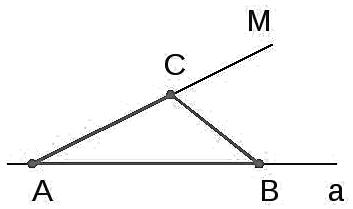
- Проведем прямую $a$ и построим на ней отрезок $AB$.
- Принимая $AB$ за одну из сторон угла, отложим от нее угол $BAM$, равный углу $α$.
- На прямой $AM$ отложим отрезок $AC$.
- Соединим точки $B$ и $C$.
Построим рисунок по составленному выше плану (рис. 1).
Из построения видно, что все начальные условия выполнены.
Так как сумма углов треугольника равняется $180^circ$. Значит, если угол α будет больше или равен $180^circ$, то задача решений иметь не будет.
В другом случае решение есть. Так как прямая $a$ – произвольная прямая, то таких треугольников будет бесконечное количество. Но, так как они все равны между собой по первому признаку, то будем считать, что решение этой задачи единственно.
Готовые работы на аналогичную тему
Построение треугольника по трем сторонам
Постройте треугольник, если нам даны три его стороны.
Пусть нам даны отрезки $AB$ и $AC$ и $BC$. Нам нужно построить треугольник $ABC$.
Составим план построения:
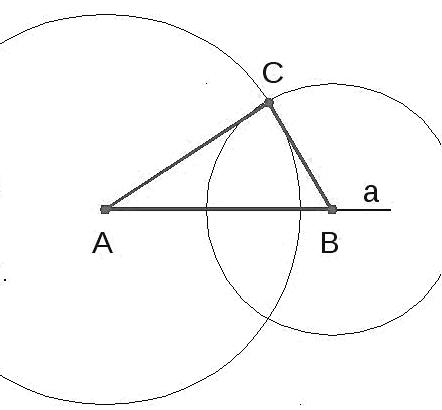
- Проведем прямую $a$ и построим на ней отрезок $AB$.
- Построим $2$ окружности: первую с центром $A$ и радиусом $AC$, и вторую с центром $B$ и радиусом $BC$.
- Соединим одну из точек пересечения окружностей (которая будет точкой $C$) с точками $A$ и $B$.
Построим рисунок по составленному выше плану (рис. 2).
Из построения видно, что все начальные условия выполнены.
Из неравенства треугольника мы знаем, что любая сторона должна быть меньше суммы двух других. Следовательно, когда такое неравенство не выполняется для исходных трех отрезков, задача решения иметь не будет.
Так как окружности из построения имеют две точки пересечения, то мы можем построить два таких треугольника. Но, так как они равны между собой по третьему признаку, то будем считать, что решение этой задачи единственно.
Построение треугольника по стороне и двум прилежащим к ней углам
Постройте треугольник, если нам дана одна стороны и углы $α$ и $β$, прилегающие к ней.
Пусть нам дан отрезок $BC$ и углы $α$ и $β$. Нам нужно построить треугольник $ABC$, где $∠B=α$, а $∠C=β$.
Составим план построения:
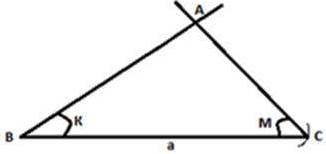
- Проведем прямую $a$ и построим на ней отрезок $BC$.
- Построим в вершине $B$ к стороне $BC$ угол $∠ K=α$.
- Построим в вершине $C$ к стороне $BC$ угол $∠ M=β$.
- Соединим точку пересечения (это и будет точка $A$) лучей $∠ K$ и $∠ M$ с точками $C$ и $B$,
Построим рисунок по составленному выше плану (рис. 3).
Из построения видно, что все начальные условия выполнены.
Так как сумма углов треугольника равняется $180^circ$, то, если $α+β≥180^circ$ задача решений иметь не будет.
В другом случае решение есть. Так как углы можем строить с двух сторон, то мы можем построить два таких треугольника. Но, так как они равны между собой по второму признаку, то будем считать, что решение этой задачи единственно.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 07 2021
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем  .
.



 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 .
.
Пример 1. Известны стороны треугольника ABC:  Найти
Найти  (Рис.1).
(Рис.1).
Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:
 .
.
 .
.
Далее, из формулы
 .
.
 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 .
.
Пример 2. Известны две стороны треугольника ABC:  и
и  (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
 ,
,
Из формулы (3) найдем cosA:
 .
.
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:
 .
.
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC:  и углы
и углы  (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:


Найдем сторону с. Из теоремы синусов имеем:
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
[spoiler title=”источники:”]
http://matworld.ru/geometry/reshenie-treugolnikov.php
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
[/spoiler]
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Соотношения между сторонами и углами треугольника
- Построение треугольника по трем его сторонам
Задача:
Построить треугольник по трем его сторонам.
Дано: отрезки МК, ОЕ, FG.
Построить 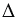 АВС так, что АВ = МК, ВС = FG, АС = ОЕ.
АВС так, что АВ = МК, ВС = FG, АС = ОЕ.
Решение:
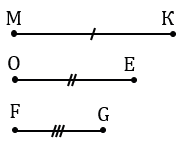
С помощью линейки проводим прямую 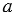 и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой
и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой 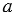 ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой
ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой 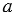 обозначаем В.
обозначаем В.
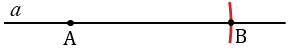
Далее, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом).

Далее, с помощью циркуля измеряем отрезок FG и строим окружность с центром в точке B радиуса FG (всю окружность строить необязательно, смотри, выделенное зеленым цветом).

Точку пересечения окружностей с центрами в точках А и В радиусами ОЕ и FG соответственно обозначаем С. Соединяем с помощью линейки точки А и В с точкой С. Получаем треугольник АВС, в котором по построению АВ = МК, ВС = FG, АС = ОЕ, следовательно, 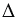 АВС – искомый.
АВС – искомый.
Данная задача не всегда имеет решение. Так как для каждого треугольника должно выполняться неравенство треугольника, которое говорит о том, что во всяком треугольнике сумма любых двух сторон больше третьей стороны. Если же какой-нибудь из данных отрезков будет больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.
Советуем посмотреть:
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный треугольники
Теорема о соотношениях между сторонами и углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Уголковый отражатель
Расстояние от точки до прямой
Расстояние между параллельными прямыми
Построение треугольника по двум сторонам и углу между ними
Построение треугольника по стороне и двум прилежащим к ней углам
Соотношения между сторонами и углами треугольника
Правило встречается в следующих упражнениях:
7 класс
Задание 291,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 292,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 313*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 315,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 630,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1300,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Построение треугольника по трем элементам
Содержание:
- Построение треугольников
- По трем сторонам
- По двум сторонам и углу
- По стороне и двум углам
- Примеры решения задач
Построение треугольников
Треугольниками называют многоугольники с тремя сторонами и аналогичным количеством вершин.
При решении задач в рамках курса геометрии нередко приходится иметь дело с этими геометрическими фигурами. Прежде, чем приступать к вычислению составных элементов, необходимо научиться построению треугольников. Справиться с этим заданием несложно. Достаточно лишь правильно идентифицировать исходные данные и применить один из распространенных способов изображения фигур:
- по паре сторон и углу, который их разделяет;
- по определенной стороне и паре углов;
- на основании данных о трех сторонах.
Существует важная закономерность, которая существенно упрощает процесс построения геометрической фигуры с тремя сторонами и углами. Речь идет о сумме всех внутренних углов, из которых складывается рассматриваемый тип многоугольника, равной 180°. Перед изображением геометрической фигуры следует подготовить канцелярские принадлежности и инструменты:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- линейка;
- циркуль;
- карандаш.
Если следовать простому алгоритму действий, то можно легко избежать ошибок. Рекомендуется придерживаться следующей последовательности и воспроизводить геометрическую фигуру поэтапно:
- Анализ условия задания. В первую очередь стоит разобраться с задачей, выписать известные величины, выявить связь между данными и искомой геометрической фигурой. В результате получится спланировать дальнейшие действия.
- Изображение треугольника. Так как план готов, можно приступать к его реализации, используя подготовленные заранее инструменты.
- Доказательство. На этой стадии необходимо идентифицировать полученное изображение, руководствуясь основными признаками и терминологией.
- Исследование. Как и во многих математических и геометрических задачах, на заключительной стадии построения треугольника требуется проанализировать количество способов и возможности решения задачи.
По трем сторонам
Представим, что известны значения трех сторон, из которых состоит треугольник. Пусть это будут стороны АВ, АС, ВС. Попробуем выполнить построение искомой геометрической фигуры, используя ранее рассмотренный алгоритм действий. Согласно обозначенной последовательности, необходимо в первую очередь проанализировать условия и спланировать работу по выполнению изображения. Порядок построения:
- провести прямую линию а с точками А и В;
- изобразить пару кругов с центрами в точках А и В;
- там, где окружности пересекаются, обозначить точку С;
- совместить с помощью прямых линий все три точки.
В результате получится треугольник АВС:
Перейдем к шагу с доказательством. Заметим, что на иллюстрации четко видно три стороны и аналогичное количество вершин изображенного многогранника. Таким образом, можно сделать вывод о построении треугольника, что и требовалось по условию задания.
Проанализируем полученную фигуру. Так как при наложении окружностей одна на другую получается лишь пара точек, в которых они пересекаются, при изображении второго подобного треугольника он совпадет с тем, что получился выше. Стоит отметить, что в треугольнике какая-либо из трех сторон всегда короче по сравнению с суммой двух других сторон. В противном случае построение многогранника с тремя сторонами и углами не представляется возможным, а у задания не будет решения.
По двум сторонам и углу
Рассмотрим другую ситуацию, когда известны величины двух сторон АВ и АС, а также угол (alpha). Требуется выполнить построение треугольника. Как и в предыдущем случае, начать решение задачи стоит с анализа условий. Изучив предоставленную информацию, целесообразно спланировать дальнейшие действия:
- построить прямую линию а;
- обозначить на полученной прямой пару точек А и В;
- изобразить угол МАВ, величина которого идентична (alpha);
- отмерить отрезок АС, который принадлежит прямой АМ;
- начертить третью сторону геометрической фигуры путем соединения точек В и С.
Наглядно результат реализации этого алгоритма выглядит следующим образом:
В процессе доказательства корректности представленного решения следует рассмотреть полученную геометрическую фигуру. Заметим, что все условия задачи соблюдены, а готовая фигура представляет собой треугольник. При исследовании рисунка становится понятно, что прямая линия а не имеет конца. Однако аналогичная линия совпадает с ней. Таким образом, данная задача обладает единственным решением при соблюдении условия о сумме внутренних углов. Если угол (alpha) равен или больше, чем 180°, то задание невозможно решить.
По стороне и двум углам
Еще один действенный способ изобразить многоугольник с тремя углами и тремя сторонами заключается в построении геометрической фигуры на основе информации о величине одной стороны и градусной мере пары углов, которые к этой стороне прилегают. Предположим, что известная сторона равна ВС, а углы соответствуют (alpha) и (beta).
Построим треугольник АВС с определенной стороной ВС, а также углами (angle К) и (angle М), равными (alpha и beta) соответственно. Тогда последовательность действий выглядит следующим образом:
- провести прямую линию а с точками В и С;
- из вершины В отложить ( angle К) на стороне ВС;
- из вершины С отложить (angle М) на стороне ВС;
- точку, где пересекаются лучи изображенных углов, обозначить А;
- провести через точку А отрезки АС и АВ.
В результате получим геометрическую фигуру в виде многогранника с тремя сторонами и тремя углами:
Итогом построения является геометрическая фигура по всем признакам соответствующая треугольнику. Если расположить углы в другую сторону, то также получится построить искомый треугольник. С другой стороны, полученная фигура аналогична первой, поэтому задача имеет единственной решение. Важным требованием является выполнение правила о сумме внутренних углов.
Примеры решения задач
Задача 1
Известны величины трех отрезков АВ, ВС, СА. Необходимо построить треугольник А1В1С1.
Источник: resh.edu.ru
Решение
Отметим прямую линию l и точку А1.
Источник: resh.edu.ru
Отложим на полученной прямой А1С1:
Источник: resh.edu.ru
Отметим точку В1:
Источник: resh.edu.ru
Соединим полученные точки, которые станут вершинами искомого треугольника.
Источник: resh.edu.ru
По результатам анализа полученного многогранника с тремя углами и тремя сторонами понятно, что изображенная геометрическая фигура является треугольником. Кроме того, у данной задачи имеется единственное решение.
Ответ: треугольник А1В1С1
Задача 2
На рисунке представлен треугольник. Необходимо вычислить, насколько вершина В удалена от стороны АС. Известны следующие величины: АВ = ВС = 10 см (angle АВС = 120°)
Источник: resh.edu.ru
Решение
Так как представленный на изображении треугольник является равнобедренным, то его высота аналогична биссектрисе. Кроме того, ВН соответствует расстоянию между точкой В и отрезком АС:
(ВН bot АС)
(angle АВН = 120° div 2 =60°)
(angle А = 30°)
Напротив вычисленного угла А расположен катет ВН, величина которого составляет по формуле ½ от величины гипотенузы. Таким образом:
(ВН = 10 div 2 = 5)
Ответ: 5 см
Построение треугольника по трем элементам
Ирина Алексеевна Антоненко
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Задачи на построение
В геометрии довольно распространены так называемые задачи на построение. Их суть заключается в том, чтобы построить какой-либо геометрический объект по какому-либо достаточному набору начальных условий имея под рукой только циркуль и линейку. Рассмотрим общую схему для выполнения таких задач:
-
Анализ задачи.
В эту часть входит установление связи между элементами, которые необходимо построить и начальными условиями задачи. После выполнения этого пункта у нас должен появиться план по решению нашей задачи.
-
Построение.
Здесь мы выполняем построения по плану, который был нами составлен выше.
-
Доказательство.
Здесь мы доказываем то, что построенная нами фигура действительно удовлетворяет начальным условиям задачи.
-
Исследование.
Здесь мы выясняем, при каких данных задача имеет одно решение, при каких несколько, а при каких ни одного.
Далее будем рассматривать задачи на построение треугольников по различным трем элементам. Здесь мы не будем рассматривать элементарные построения, таких как отрезок, угол и т.д. К этому моменту эти навыки уже у Вас должны иметься.
Построение треугольника по двум сторонами и углу между ними
Пример 1
Постройте треугольник, если нам даны две стороны и угол, который находится между этими сторонами.
Анализ.
Пусть нам даны отрезки $AB$ и $AC$ и угол $α$. Нам нужно построить треугольник $ABC$ с углом $C$ равным $α$.
Составим план построения:
- Проведем прямую $a$ и построим на ней отрезок $AB$.
- Принимая $AB$ за одну из сторон угла, отложим от нее угол $BAM$, равный углу $α$.
- На прямой $AM$ отложим отрезок $AC$.
- Соединим точки $B$ и $C$.
Построение.
Построим рисунок по составленному выше плану (рис. 1).
Доказательство.
Из построения видно, что все начальные условия выполнены.
Исследование.
Так как сумма углов треугольника равняется $180^circ$. Значит, если угол α будет больше или равен $180^circ$, то задача решений иметь не будет.
В другом случае решение есть. Так как прямая $a$ – произвольная прямая, то таких треугольников будет бесконечное количество. Но, так как они все равны между собой по первому признаку, то будем считать, что решение этой задачи единственно.
«Построение треугольника по трем элементам» 👇
Построение треугольника по трем сторонам
Пример 2
Постройте треугольник, если нам даны три его стороны.
Анализ.
Пусть нам даны отрезки $AB$ и $AC$ и $BC$. Нам нужно построить треугольник $ABC$.
Составим план построения:
- Проведем прямую $a$ и построим на ней отрезок $AB$.
- Построим $2$ окружности: первую с центром $A$ и радиусом $AC$, и вторую с центром $B$ и радиусом $BC$.
- Соединим одну из точек пересечения окружностей (которая будет точкой $C$) с точками $A$ и $B$.
Построение.
Построим рисунок по составленному выше плану (рис. 2).
Доказательство.
Из построения видно, что все начальные условия выполнены.
Исследование.
Из неравенства треугольника мы знаем, что любая сторона должна быть меньше суммы двух других. Следовательно, когда такое неравенство не выполняется для исходных трех отрезков, задача решения иметь не будет.
Так как окружности из построения имеют две точки пересечения, то мы можем построить два таких треугольника. Но, так как они равны между собой по третьему признаку, то будем считать, что решение этой задачи единственно.
Построение треугольника по стороне и двум прилежащим к ней углам
Пример 3
Постройте треугольник, если нам дана одна стороны и углы $α$ и $β$, прилегающие к ней.
Анализ.
Пусть нам дан отрезок $BC$ и углы $α$ и $β$. Нам нужно построить треугольник $ABC$, где $∠B=α$, а $∠C=β$.
Составим план построения:
- Проведем прямую $a$ и построим на ней отрезок $BC$.
- Построим в вершине $B$ к стороне $BC$ угол $∠ K=α$.
- Построим в вершине $C$ к стороне $BC$ угол $∠ M=β$.
- Соединим точку пересечения (это и будет точка $A$) лучей $∠ K$ и $∠ M$ с точками $C$ и $B$,
Построение.
Построим рисунок по составленному выше плану (рис. 3).
Доказательство.
Из построения видно, что все начальные условия выполнены.
Исследование.
Так как сумма углов треугольника равняется $180^circ$, то, если $α+β≥180^circ$ задача решений иметь не будет.
В другом случае решение есть. Так как углы можем строить с двух сторон, то мы можем построить два таких треугольника. Но, так как они равны между собой по второму признаку, то будем считать, что решение этой задачи единственно.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 12.07.2022
Геометрия
7 класс
Урок № 27
Построение треугольника по трём элементам
Перечень вопросов, рассматриваемых в теме:
- Задачи на построение циркулем и линейкой.
- Алгоритмы решения простейших задач на построение.
- Способы решения задач на построение треугольника по трём заданным элементам.
- Этапы решения задач на построение: анализ, построение, доказательство, исследование.
Тезаурус:
Задачей на построение называется предложение, указывающее, по каким данным, какую геометрическую фигуру требуется построить, чтобы эта фигура удовлетворяла определённым условиям.
Построение треугольника по трём элементам:
- по 2 сторонам и углу между ними;
- по стороне и двум прилежащим к нему углам;
- по трём сторонам.
Задачи на построение:
- позволяют моделировать те или иные практические ситуации
- устанавливают связь между геометрией и черчением, геометрией и рисованием.
Основная литература:
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения
Построение треугольника по трём элементам.
Чтобы построить треугольник, нужно уметь строить:
1. Отрезок, равный данному.


2. Угол, равный данному.

Любая задача на построение включает в себя четыре основных этапа.
Анализ: предположить, что задача решена, сделать чертеж от руки искомой фигуры, составить план решения задачи.
Построение: описать способ построения.
Доказательство: доказать, что построенная фигура или множество точек – искомые.
Исследование: выяснить, всегда ли построение возможно.
Задача 1.
Построить треугольник по трём заданным сторонам.
Условие:
Дано:

Построить: ∆A1B1C1 = ∆ABC
Схема построения:




Задача 2.
Построить треугольник по двум сторонам и углу между ними.
Условие:
Дано:

Построить: ∆A1B1C1 такой, что A1B1 = AB, A1C1 = AC, ∠B1A1C1 = ∠BAC.
Схема построения:



Задача 3.
Построить треугольник по стороне и двум прилежащим к ней углам.
Условие:
Дано:

Построить: ∆A1B1C1 такой, что A1B1 = AB, ∠A1 = ∠A, ∠B1 = ∠B.
Схема построения:



Разбор решения заданий тренировочного модуля.
Задача 1. Найдите расстояние от вершины В до прямой АС.
Дано. В треугольнике АВС: АВ = ВС = 10 см, ∠АВС = 120°.

Решение.
∆АВС – равнобедренный. ВН – расстояние от точки В до прямой АС, т. е. ВН ⊥ АС. В равнобедренном треугольнике высота является биссектрисой. ∠АВН = 120°: 2 =60°, значит, ∠А = 30°. Против угла 30° лежит катет ВН равный половине гипотенузы АВ. Значит, ВН = 10 : 2 = 5 см.
Ответ: 5 см расстояние от вершины В до прямой АС.
Задача 2. Построить прямоугольный треугольник по гипотенузе и острому углу.
Дано: отрезок р, угол α.

Решение.
- Построим ∠В = α.
- Проведем окружность с центром В и радиусом р.
- С – точка пересечения окружности и угла.
- Построим перпендикуляр к другой стороне угла.
- ∆АВС – искомый.
Задача 3. Построить треугольник по стороне, прилежащему к ней углу и биссектрисе треугольника, проведенной из вершины этого угла.
Дано: отрезки р и q, угол α.
Решение.
Требуется построить треугольник АВС, у которого одна из сторон, например АС = р, ∠А =α , а биссектриса АD = q.

Построение:
1) Построим ∠А = α.
2) Отложим отрезок АС = р.
3) Построим биссектрису АD угла А.
4) Отложим отрезок АD = q.
5) В – точка пересечения АВ и СD.
∆АВС – искомый.
Ответ: ∆АВС – искомый.