Изобретение относится к измерительной технике, а именно к определению собственных частот колебаний элементов конструкций и деталей машин в виде балки или пластинки на стенде. Цель изобретения – повышение точности определения собственных частот колебаний ненагруженных элементов конструкций за счет дополнительного их нагружения равномерно распределенной нагрузкой. Действительная частота колебаний ненагруженного элемента определяется путем пересчета с учетом регистрируемой частоты колебаний элемента с дополнительной нагрузкой.
СОЮЗ СОВЕТСКИХ
СОЦИАЛИСТИЧЕСКИХ
РЕСПУБЛИК
ГОСУДАРСТВЕННЫЙ КОМИТЕТ
ПО ИЗОБРЕТЕНИЯМ И ОТКРЫТИЯМ
ПРИ ГКНТ СССР
ОПИСАНИЕ ИЗОБРЕТЕНИЯ
1 I 4 2 п1+Я вЂ” 1+
К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ (21) 4484964/25-28 (22) 20.09.88 (46) 15.12.90. Бюл. и 46 (71) Ставропольский политехнический институт (72) В.И. Коробко, Н.Д. Идрисов и Г.В, Слюсарев (53) 620.178.324 (088.8) (56) Лупин О.B. и др, Обследование и испытание сооружений,.M.: Стройиздат, 1987, с, 264. (54) СПОСОБ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ ИЗГИБНЫХ КОЛЕБАНИЙ
ЭЛЕМЕНТОВ КОНСТРУКЦИЙ НА СТЕНДЕ. Изобретение относится к измерительной технике; а именно к определению собственных частот колебаний элементов конструкций и деталей машин на стенде, и может быть использовано для динамических испытаний строительных конструкций в заводских условиях.
Цель изобретения — повышение точности определения частоты свободных колебаний элементов конструкций.
Поставленная цель достигается тем, что перед возбуждением свободных колебаний конструкцию нагружают дополнительной нагрузкой. В результате действия этой нагрузки происходит более плотное прилегание опорных граней элемента конструкции к опорным устройствам, что значительно уменьшает влияние дефектов опирания на частоту свободных колебаний.
Известно, что основная частота колебаний балки может быть определена по формуле Ж 1о13902 А1 (Я)5 G 01 M 7/00 (57) Изобретение относится к измерительной технике, а именно к определению собственных частот колебаний элементов конструкций и деталей машин в виде балки или пластинки на стенде. Цель изобретения — повышение точности определения собственных частот колебаний ненагруженных элементов конструкций за счет дополнительного их нагружения равномерно распределенной нагрузкой. Действительная частота колебаний ненагруженного элемента определяется путем пересчета с учетом регистрируемой частоты колебаний элемента с дополнительной нагрузкой.
I где в- основная частота (круговая) колебаний балки; а — коэффициент, зависящий от вида граничных условий;
1 — длина (пролет) балки;
El — жесткость сечения балки;
m — погонная масса балки.
Если балку нагрузить дополнительной, равномерно распределенной нагрузкой, погонная масса которой m, то.где N- основная (круговая) частота колебаний балки с дополнительной равномерно распределенной нагрузкой.
Разделим выражение (1) на (2):
Отсюда находим
g ) (+ . = /(+; „, Ю . qg где q — интенсивность дополнительной равномерно распределенной нагрузки;
q — интенсивность нагрузки от собственного веса балки; .
g — ускорение свободного падения.
Аналогичная формула получается и для элементов конструкций в виде плиты.
Действительно, для плиты
10 ветствии с требованиями ГОСТ 8829-85, Такое размещение блоков соответствует эквивалентной равномерно распределенной нагрузке q – -345 кг. В плите с пригрузом возбуждают свободные колебания с помощью специального ударного устройства (электромагнитная пушка), Частоту свободных колебаний регистрируют с помощью самописца и она равна f == 9,41 Гц.
По формуле (5) определяем частоту колебаний плиты без пригруза = ((+ тi (4) сЭ где в, в- соответственно основные частоты колебаний плиты без догружения и с пригрузом;
0 — цилиндрическая жесткость плиты;
А — площадь пластинки.
Перейдя от круговой частоты колебаний в к частоте f, получаем = t+ qq . (5)
Величина пригруза определяется для конкретного элемента конструкции отдельно, но не должка вызывать в элементе появление пластических деформаций или трещин (для железобетонных изделий), Таким образом, дополнительное нагружение элемента конструкции равномерно распределенной нагрузкой позволяет достичь цели изобретения.
Этот способ реализуется как для элементов конструкций в виде балки, так и в виде плиты.
Сравнение основных частот колебаний, полученных с помощью предлагаемого способа, с результатами непосредственного испытания некагруженных элементов конструкций показало отличие результатов на
2-5 . Это свидетельствует о повышении точности измерений с помощью предлагаемого способа.
Пример. Необходимо определить основную частоту свободных колебаний железобетонной предварительно напряженной плиты перекрытия ПТК58-12, шарнирно опираемой в сооружении. Длина плиты1=
= 5,8 м; вес P = 2,8 т (q = 0,483м). После установки плиты на стенде ее нагружают дополнительно четырьмя одинаковыми железобетонными блоками общим весом P =
=2000 кг. Блоки размещают на плите так, что расстояние между их центрами составляет
1/41 = 145 см, а расстояние от центра первого блока до опоры 1/8I = 72,5 см (в соотf = 9,41 / 1 + — = 12,32Гц
483
15.
Плиту также испытывают без дополнительного пригруза. При этом регистрируют частоту колебаний f = 12,02 Гц.
Предлагаемый способ обеспечивает плотное прилегание опорной грани плиты к опорным устройствам стенда и тем самым способствует повышению точности определения основной частоты свободных колебаний ненагруженной плиты. В указанном примере уточнение составляет 2 .
Использование предлагаемого способа позволяет повысить точность измерения основной частоты колебаний ненагруженных элементов конструкций, что важно при последующей оценке качества иэделия.
Формула изобретения
Способ определения собственных частот .изгибных колебаний элементов конструкций на стенде, заключающийся в том, что устанавливают контролируемый элемент на стенд, закрепляют его концы в соответствии со схемой его работы в сооружении, возбуждают свободные колебания и регистрируют собственную частоту колебаний, о т л и ч аю шийся тем, что, с целью повышения точности определения частоты колебаний, элемент конструкции перед возбуждением свободных колебаний нагружают дополнительной равномерно распределенной нагрузкой, величина которой не вызывает пластических деформаций и трещинообразования, а собственную частоту колебаний контролируемого элемента без пригруза определяют с учетом собственной частоты колебаний этого элемента с пригрузом по формуле
=(т+ i,: где f — частота собственных колебаний элемента конструкции без пригруза;
f — частота собственных колебаний элемента конструкции с пригрузом;
q — интенсивность дополнительной нагрузки;
q — интенсивность собственной массы элемента конструкции.
1613902
Составитель О.Несова
Техред M.Ìîðãåíòàë Корректор М.Шарощи
Редактор С.Лисина
Производственно-издательский комбинат “Патент”, г. Ужгород, ул.Гагарина, 101
Заказ 3887 Тираж 441 Подписное
ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ СССР
113035, Москва, Ж-35, Раушская наб., 4/5




- Как найти период и частоту колебаний
- Как найти резонансную частоту
- Как измерить частоту
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы: – скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
– скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
– число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Формулы для вычисления периода простейших колебательных систем
Период колебаний пружинного маятника определим как:
[T=2pi sqrt{frac{m}{k}} left(3right),]
на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.
Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)
[T=2pi sqrt{frac{l}{g}}left(4right).]
Формула для вычисления периода колебаний физического маятника представляет собой выражение:
[T=2pi sqrt{frac{J}{mga}left(5right),}]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние от центра масс тела до оси вращения.
Единицами измерения периода служат единицы времени, например секунды.
[left[Tright]=c.]
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
.
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Частота гармонических колебаний
При работе с колебательными процессами нередки случаи, когда для характеристики «скорости» удобнее рассматривать не период одного колебания, а количество колебаний за единицу времени. Такая величина называется частотой колебаний, и обозначается греческой буквой $nu$ («ню»). Она равна отношению числа колебаний ко времени, за которое они происходят:
$$nu={Nover t},$$
где:
- N – число колебаний;
- t – время, за которое колебания произошли (сек).
Поскольку единицей времени в системе СИ является секунда, то единицей частоты является «колебание в секунду», или Герц (Гц).

Рис. 3. Частота колебаний.
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Период гармонических колебаний
Особенностью гармонических колебаний является их большая схожесть. Каждое колебание маятника почти полностью повторяет предыдущее и последующее.
В первую очередь это относится к «скорости качания». Если измерить время, за которое совершаются колебания маятника, можно убедиться, что оно для разных колебаний остается одинаковым. Взяв много маятников разных длин, можно получить различные колебания, однако, для каждого маятника время, за которое совершается любое колебание, будет постоянным.
Это время – важнейшая характеристика колебательного процесса. Оно называется периодом колебаний, обозначается латинской буквой $T$ и измеряется в секундах. Чем быстрее происходят колебания (чем короче нить маятника), тем меньше времени длится каждое колебание, и тем меньше период колебаний.

Рис. 2. Период колебаний.
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
Циклическая частота характеризует скорость изменения фазы колебаний.
Начальное состояние колебательной системы характеризует начальная фаза
Амплитуда колебаний A — это наибольшее смещение из положения равновесия
Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний — это число полных колебаний в единицу времени t.
Частота, циклическая частота и период колебаний соотносятся как
Связь периода и частоты колебаний
Из формулы частоты колебаний можно получить зависимость периода колебаний от частоты. Если колебания происходят с периодом $T$, то $N$ колебаний произойдут за время $TN$. Подставив это время в формулу, получим:
$$nu={Nover t}={Nover TN}={1over T}$$
Таким образом, частота и период колебаний взаимнообратны. Зная частоту – легко найти период, а зная период – легко найти частоту.
Из математики известно, что на нуль делить нельзя. То есть, в формулу связи периода и частоты колебаний нельзя подставлять нулевой период или частоту – в обоих случаях такие колебания невозможны.
Виды колебаний
Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).
Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).
При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Математический маятник
Обычный нитяной маятник представляет собой груз, подвешенный на нити, способный совершать колебательные движения после выведения его из состояния равновесия. Для описания движения такого маятника удобно использовать модель, называемую математическим маятником. Математический маятник имеет следующие отличия от реального маятника.
- Математический маятник, в отличие от реального маятника, не получает и не теряет энергию, трение в математическом маятнике принимается равным нулю.
- Масса математического маятника представляет собой материальную точку, закрепленную на конце нити. Другой конец неподвижен в принятой Системе Отсчета.
- Гравитационное поле, в котором маятник совершает колебания, однородно и направлено в сторону от точки закрепления нити к точке равновесия маятника.
- Нить не имеет веса, и не изменяет свою длину.

Рис. 1. Математический маятник.
Для того, чтобы обычный нитяной маятник хорошо описывался формулами математического маятника, необходимо, чтобы его груз имел малый размер, нить была бы нерастяжимой, и максимальное отклонение маятника было бы намного меньше (более, чем в 10 раз) его длины.
Вынужденные колебания. Резонанс
Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.
Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.
Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.
Формула периода колебаний
Для определения формулы периода колебаний математического маятника учтем, что колебания совершаются по некоторой дуге. Радиус этой дуги равен длине нити $l$, угол, на который происходит отклонение, обозначим $α$. Мгновенная скорость материальной точки всегда направлена по касательной к траектории, а значит, для математического маятника мгновенная скорость направлена по касательной к этой дуге. Проекция силы тяжести на нее будет равна:
$$F=-mgsinalpha$$
Ускорение движения материальной точки находится по второму закону Ньютона. После проецирования получаем:
$$a_т={Fover m}$$
После подстановки можно сократить массу, получаем:
$$a_т=-gsinalpha$$
Для малых углов дуги $sinalpha=alpha$ и $s=alpha l$, поэтому:
$$a_т=-{gover {l}}s$$
Ускорение – это вторая производная перемещения. Единственная функция, производная которой пропорциональна самой себе со знаком минус – это круговая функция (синусоида). То есть, решение полученного уравнения:
$$s(t)=S_{max} cos sqrt{gover l}t$$

Рис. 2. График колебаний математического маятника.
Периодом этой функции (а, значит, и периодом колебаний математического маятника) будет величина:
$$T=2pisqrt {lover g}$$
Данная формула была установлена Х. Гюйгенсом.
Отметим, что формула периода колебаний математического маятника очень похожа на формулу колебаний пружинного маятника. Ускорение свободного падения в математическом маятнике соответствует жесткости пружины в пружинном маятнике. Длина маятника соответствует массе груза. Это объясняется тем, что в обоих случаях причиной колебаний является сила, зависящая от отклонения, направленная против него.

Рис. 3. Нитяной и пружинный маятники.
Примеры резонанса
Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.
В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.
Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.
Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
Колебания и их амплитуда
Повторяющиеся движения или процессы называют колебаниями
.
В зависимости от природы колебания могут быть механическими, электромагнитными, звуковыми и др. Разные виды колебаний описывают с помощью одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания называют свободными
(иди собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешних воздействий на эту систему нет.
Самым простым видом колебаний являются гармонические колебания.
Гармоническими колебаниями
называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса..
Пусть происходят гармонические колебания некоторого параметра $s$, тогда эти колебания можно описать при помощи следующего уравнения:
где $A=s_ $ — амплитуда колебаний; $ _0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $( _0t+varphi )$ — фаза колебаний.
Амплитудой называют максимальной значение величины, колебания которой рассматривают. Так как косинус (как и синус) изменяется в пределах от единицы до минус единицы, то величина $s$ находится в пределах $-Ale sle $+A.
Колебательные процессы
Колебательным процессом называется периодическое изменение одного или нескольких параметров системы около некоторого значения. Например, колебательным процессом является флаг, развевающийся на ветру. Полотнище флага совершает хаотичные движения вокруг некоторого среднего положения, задаваемого ветром. Другим примером колебательного процесса является движение нитяного маятника – если груз, подвешенный на нити, отклонить от положения равновесия и отпустить, то он начинает колебаться вокруг положения равновесия.
В первом приведенном примере колебания являются хаотичными. Во втором примере – колебания подчиняются простому закону круговых функций (синусоиды), и называются гармоническими. В высшей математике доказывается, что любые сложные колебания могут быть описаны суммой гармонических колебаний. Поэтому в первую очередь изучаются именно они.

Рис. 1. Колебания в природе.
Задачи на Механические колебания с решениями
Формулы, используемые на уроках «Задачи на Механические колебания».
Название величины |
Обозначение |
Единица измерения |
Формула |
Амплитуда колебаний |
A |
м |
|
Период колебаний |
T |
с |
T = 1 / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = 1 / T ;v = N / t |
Число колебаний за какое-то время |
N |
N = t /T ;N = vt |
|
Время |
t |
с |
t = NT ;t = N / v |
Циклическая частота колебаний |
ω |
Гц |
|
Период колебаний пружинного маятника |
T |
c |
|
Период колебаний математического маятника |
T |
c |
|
Уравнение гармонических колебаний |
x(t) = Asin(ωt+φ0) |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2.
На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3.
Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4.
Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.


Задача № 5.
Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.

Задача № 6.
Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7.
Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
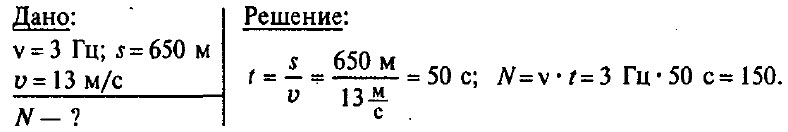
Задача № 8.
Гармоническое колебание описывается уравнением
![]() Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9.
Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
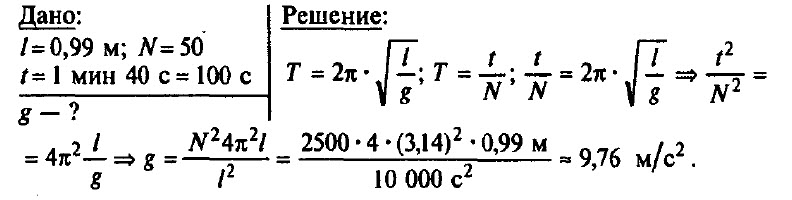
Задача № 10.
ОГЭ
Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11.
ЕГЭ
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.


Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Пример 9.2. Рассчитать колебания фундамента штамповочного молота. Штамповочные молоты относятся к типу машин с импульсными нагрузками, по этому необходимо обеспечить допустимый уровень вибраций путем рационального подбора площади подошвы и массы фундамента. Исходные данные: молот паровоздушный, штамповочный модели 17 КП, масса падающих частей (с учетом массы верхнего штампа) ![]() = 5 т, масса молота mh = 40 т; масса шабота man = 100 т, максимальная энергия удара Esh = 191,9 кДж, площадь шабота Aаn = 5,6 м2 ; отметка подошвы шабота от уровня пола цеха 2,125 м, материал штампуемых изделий — сталь.
= 5 т, масса молота mh = 40 т; масса шабота man = 100 т, максимальная энергия удара Esh = 191,9 кДж, площадь шабота Aаn = 5,6 м2 ; отметка подошвы шабота от уровня пола цеха 2,125 м, материал штампуемых изделий — сталь.
Площадка строительства на глубину 1,5—2 м сложена насыпными грунтами, далее, на глубину 8—10 м залегают суглинки полутвердые, подстилаемые глинами тугопластичной консистенции (толщина изученного слоя 5—6 м). Подземные воды не обнаружены. Следовательно, основанием фундамента молота будут служить суглинки с расчетным сопротивлением R = 250 кПа и модулем деформации E = 1,6·104 кПа.
Материал фундамента — бетон класса по прочности на сжатие M 200, марки по морозостойкости F50. Арматура — сталь круглая, горячекатаная классов A-I и A-II. Подшаботная прокладка из дубовых брусьев I сорта по ГОСТ 2695-83.
Решение. Высота фундамента при отметке низа шабота относительно пола цеха 2,125 м, толщине подшаботной прокладки (предварительно принимается из трех рядов дубовых брусьев площадью сечения 10×15 см) tω = 0,45 м и толщине подшаботной части фундамента 2,25 м (для молотов с массой падающих частей 4 < m0 ≤ 6 т) должна быть не менее: hf = 2,125 + 0,45 + 2,25 = 4,825 м. Размеры подошвы фундамента предварительна принимаются равными 6,5×8 м.
Окончательные размеры фундамента назначаются после проверки динамического давления на подшаботную прокладку, среднего статического давления на основание, амплитуд колебании фундамента с учетом инженерно-геологических условий площадки строительств и конструктивного решения соседних фундаментов зданий и оборудования.
Скорость падающих частей молота в момент удара
![]() м /с.
м /с.
Расчетное динамическое давление на подшаботную прокладку определяем по формуле
![]()
где Eω = 5·105 кПа — модуль упругости древесины из дуба,
m‘1 = mh + man = 40+100 = 140 т.
Тогда
![]() 2583,3 кПа < σadm = 3600 кПа.
2583,3 кПа < σadm = 3600 кПа.
Принятая толщина подшаботной прокладки достаточна.
Принимаем высоту фундамента 4,9 м. Масса подшаботной прокладки mω = 0,45·2,5·3,2 — 0,85 = 3,1 т.
Масса фундамента mf = (6,5 · 8,0 · 4,9 – 3,2 · 2,5 · 2,575)2,4 = 562,1 т.
Проверяем условие (9.1) при γс0 = 0,5 и γс1 = 1:
![]() 135,6 кПа > 0,5·1·250 = 125 кПа.
135,6 кПа > 0,5·1·250 = 125 кПа.
Следовательно, необходимо увеличить площадь фундамента, уменьшить массу фундамента или принять фундамент свайным.
По периметру фундамента принимаем уступ шириной 1 м, высотой 1 м (рис. 9.2).
Тогда масса фундамента
![]() т
т
а масса грунта на уступах фундамента
![]() т
т
Проверяем условие (9.1):
![]()
= 119,5 кПа < 0,5·1·250 = 125 кПа.
Определение амплитуды вертикальных колебаний фундамента производится по формуле
![]() ,
,
где ε = 0,5 — коэффициент восстановления скорости удара при штамповке стальных изделий.
Вычисляем необходимые для расчета параметры: по формуле (9.6)
 кН/м3;
кН/м3;
по формуле (9.8)
![]() кН/м;
кН/м;
по формуле (9.14)
 ,
,

Рис. 9.2. Фундамент штамповочного молота 17КП
при m = 1016,1 т
![]() с–1;
с–1;
![]() Гц.
Гц.
Подставляя найденные значения в формулу, получаем:
![]()
= 0,00079 м = 0,79 мм < Aadm = 1,2 мм.
Пример 9.3. Рассчитать колебания рамного фундамента электрической машины. Исходные данные: масса машины mm = 32,6 т (m1 = 8,4 т, 2m2 = 24,2 т); нормативная горизонтальная динамическая сила Fn = 13,5 кН; частота вращения главного вала nr = 600 мин–1; допускаемая амплитуда колебаний фундамента Aadm = 0,15 мм
В основании фундамента залегают тугопластичные глины, имеющие модуль деформации E = 1,5×104 кПа, расчетное сопротивление на основание R = 250 кПа.
Схема фундамента приведена на рис. 9.3. где Q1 =m1g; Q2 = m2g. Составляющими частями фундамента являются нижняя плита из монолитного железобетона, сборные железобетонные колонны и ригели (три поперечные рамы) и верхняя плита из сборного железобетона (базовая конструкция).

Рис. 9.3. Фундамент электрической машины
Бетон нижней плиты марки M 200, сборных элементов M 300. Сечение колонн 400×400 мм, ригелей 300×500 мм.
Решение. Упругие характеристики основания фундамента определяем следующим образом; но формуле (9.6) при A = 3,6·6,0 = 21,6 м2
![]() кН/м3;
кН/м3;
по формуле (9.7):
![]() кН/м3;
кН/м3;
![]() кН/м3;
кН/м3;
![]() кН/м3;
кН/м3;
по формуле (9.9)
![]() кН/м;
кН/м;
по формуле (9.10) при ![]() м4
м4
![]() кН/м;
кН/м;
по формуле (9.11) при ![]() м4
м4
![]() кН/м.
кН/м.
Коэффициенты относительного демпфирования основания определяются, если угловая частота вращения машины отличается менее чем на 25 % от собственных угловых частот колебаний установки.
Коэффициенты жесткости конструкции фундамента с учетом упругости основания в горизонтальном направлении, перпендикулярном оси вала машины, и при повороте в горизонтальной плоскости находим по формулам:
![]() ;
; ![]() .
.
где h = 6,5 м — высота фундамента.
Для определения
![]()
(сумма коэффициентов жесткости всех поперечных рам в горизонтальном направлении, перпендикулярном оси вала машины) и ![]() (то же, при повороте верхней плиты в горизонтальной плоскости относительно ее центра тяжести) необходимо вычислить дополнительные параметры:
(то же, при повороте верхней плиты в горизонтальной плоскости относительно ее центра тяжести) необходимо вычислить дополнительные параметры:
e1 = e3 = 2,5 м; e2 = 0;
![]() ;
;
![]() кПа;
кПа;
![]() ;
;
![]() м4 ;
м4 ;
![]() м4 ;
м4 ;
![]() м ;
м ;
![]() м ;
м ;
![]() ;
;
![]() кН/м.
кН/м.
Подставляя найденные значения, получаем:
![]() кН/м;
кН/м;
![]() кН·м.
кН·м.
Теперь находим коэффициенты жесткости:
![]() кН/м;
кН/м;
![]() кН·м.
кН·м.
Угловая частота собственных горизонтальных колебаний фундамента
![]() .
.
где ![]() — масса системы, включающая массу машины, верхней плиты m1, ригелей m2 и 30 % массы всех колонн фундамента m (m1 = 2,4·0,4·3,0·5,5 = 15,84 т; m2 = 3·2,4·0,3·3,0 = 3,24 т; m3 = 6·2,4·0,4·0,4·4,6 = 10,6 т)
— масса системы, включающая массу машины, верхней плиты m1, ригелей m2 и 30 % массы всех колонн фундамента m (m1 = 2,4·0,4·3,0·5,5 = 15,84 т; m2 = 3·2,4·0,3·3,0 = 3,24 т; m3 = 6·2,4·0,4·0,4·4,6 = 10,6 т)
![]() = 32,6 + 15,84 + 3,24 + 0,3·10,6 = 56 т.
= 32,6 + 15,84 + 3,24 + 0,3·10,6 = 56 т.
Подставляя в формулу значение ![]() , получаем:
, получаем:
![]() с–1.
с–1.
Угловая частота собственных вращательных колебаний фундамента относительно вертикальной оси, проходящей через центр тяжести верхней плиты,
![]() с–1,
с–1,
где ![]() т·м2 (здесь l = 5,5 — длина верхней плиты).
т·м2 (здесь l = 5,5 — длина верхней плиты).
Для определения амплитуды горизонтально-крутильных колебаний верхней плиты фундамента,
![]() ,
,
где lmax = 2,5 м (расстояние от центра тяжести верхней плиты до оси наиболее удаленного подшипника машины), следует вычислить:
 ;
;
 .
.
Находим дополнительные параметры для расчета по этим формулам:
![]() с–1;
с–1;
![]() м ;
м ;
где ![]() кН;
кН;
![]() рад,
рад,
где ![]() кН·м.
кН·м.
Поскольку угловая частота вращения машины ω = 63 с–1 отличается более чем на 25 % от угловых частот собственных колебаний λx = 17,9 с–1 и λψ = 28 с–1, принимаем ξ’x = 0 и ξ’ψ = 0.
Подставляя найденные значения в соответствующие формулы, получаем:
![]() м;
м;
![]() рад.
рад.
Вычисляем значение амплитуды:
Ah = 0,066·10–3 + 0,031·10–3·2,5 = 0,144·10–3 м = 0,144 мм < Aadm = 0,15 мм.
Сообщения без ответов | Активные темы | Избранное
|
|
Задача из Савченко на колебания плиты
|
|
18/12/17 |
Условие: 3.3.32. На горизонтальной плите лежит груз. Плита начинает двигаться Мой ход рассуждений. Пусть Известно, что
Также известна формула Далее распишем ЗСЭ для шарика в момент отрыва:
|
|
|
|
|
Pphantom |
Posted automatically
|
||
09/05/12 |
|||
|
|
|||
|
Pphantom |
Posted automatically
|
||||
09/05/12 |
|
||||
|
|
|||||
|
DimaM |
Re: Задача из Савченко на колебания плиты
|
||
28/12/12 |
С ответом не совпадает. Что именно не совпадает?
|
||
|
|
|||
|
EUgeneUS |
Re: Задача из Савченко на колебания плиты
|
|
11/12/16 |
Как всё сложно. И вот это к чему, зачем нам а Но что удивительно, если довести решение до ответа, получается, как у меня: И еще надо условие наложить: — 30.08.2018, 12:35 — Учитываете ли вы, что начальное положение – это не положение равновесия при колебаниях? Ну вот. Как раз про: Могут быть нюансы – с какой фазы плита начинает двигаться гармонически.
|
|
|
|
|
DimaM |
Re: Задача из Савченко на колебания плиты
|
||
28/12/12 |
А в решебнике какой ответ? То задачник, а не решебник
|
||
|
|
|||
|
EUgeneUS |
Re: Задача из Савченко на колебания плиты
|
|
11/12/16 |
DimaM При некотором размышлении разумная фаза – единственная. inevitablee 1. Запишите гармонический закон в общем виде:
|
|
|
|
|
inevitablee |
Re: Задача из Савченко на колебания плиты
|
|
18/12/17 |
EUgeneUS 3.3.32.
У меня получается то же, что и у вас. А почему начальное положение – не положение равновесия при колебаниях? Я от него и отсчитывал амплитуду.
|
|
|
|
|
EUgeneUS |
Re: Задача из Савченко на колебания плиты
|
|
11/12/16 |
inevitablee А почему Вы решили, что плита начинает совершать гармонические колебания начиная с положения равновесия?
|
|
|
|
|
inevitablee |
Re: Задача из Савченко на колебания плиты
|
|
18/12/17 |
EUgeneUS То есть может быть так, что она поднялась вверх и только потом начала колебания?
|
|
|
|
|
EUgeneUS |
Re: Задача из Савченко на колебания плиты
|
|
11/12/16 |
|
|
|
|
|
Pphantom |
Posted automatically
|
||
09/05/12 |
|||
|
|
|||
|
Pphantom |
Posted automatically
|
||||
09/05/12 |
|
||||
|
|
|||||
|
inevitablee |
Re: Задача из Савченко на колебания плиты
|
|
18/12/17 |
1. Секунду, то есть положение равновесия достигается где-то на пути к верхней точке траектории, так?
|
|
|
|
|
DimaM |
Re: Задача из Савченко на колебания плиты
|
||
28/12/12 |
откуда Не, нужно
|
||
|
|
|||
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
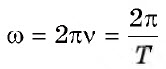
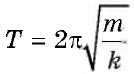
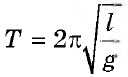
 и амплитудой
и амплитудой . На какую высоту от начального положения плиты подскочит груз после
. На какую высоту от начального положения плиты подскочит груз после -масса шарика, а
-масса шарика, а  – масса плиты. Направим ось X вниз и распишем условие отрыва для шарика:
– масса плиты. Направим ось X вниз и распишем условие отрыва для шарика:  , отрыв при
, отрыв при  , поэтому при отрыве
, поэтому при отрыве  . Здесь можно воспользоваться формулой эллиптической связи:
. Здесь можно воспользоваться формулой эллиптической связи:  , где
, где  – максимальное ускорение плиты, а
– максимальное ускорение плиты, а  – максимальная скорость.
– максимальная скорость. , а
, а  , где
, где  . Подставим это в первое условие и выразим скорость плиты(и шарика)
. Подставим это в первое условие и выразим скорость плиты(и шарика) в момент отрыва шарика:
в момент отрыва шарика: .
. , связывающая координату тела и его ускорение в этой координате при колебаниях.
, связывающая координату тела и его ускорение в этой координате при колебаниях. .
. , где
, где  и есть искомая высота, отсчитываемая от линии начала движения плиты. Затем сюда подставляем значения
и есть искомая высота, отсчитываемая от линии начала движения плиты. Затем сюда подставляем значения  . С ответом не совпадает. Что не так в моих рассуждениях?
. С ответом не совпадает. Что не так в моих рассуждениях? ?
?
 , иначе шарик никогда не оторвется от плиты.
, иначе шарик никогда не оторвется от плиты. , это как раз про ваше замечание ниже.
, это как раз про ваше замечание ниже.
 – скорость массивной плиты не может измениться скачком, найдите фазу колебаний.
– скорость массивной плиты не может измениться скачком, найдите фазу колебаний. – это и будет значение
– это и будет значение 
 , так чтобы производная не имела разрыва.”
, так чтобы производная не имела разрыва.”
 , куда подставим условие
, куда подставим условие  .
.
 , откуда
, откуда  . Если это подставить в первое выражение и найти
. Если это подставить в первое выражение и найти  , откуда
, откуда  . Это значит, что в начале он находится в амплитудном положении.
. Это значит, что в начале он находится в амплитудном положении. , но к самому первому уравнению можно добавить константу.
, но к самому первому уравнению можно добавить константу.