Как найти площадь грани куба
Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками – квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.

Инструкция
Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.
Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:
S = a², где а – сторона квадрата (ребро куба).
Пример: Длина ребра куба 11 см, требуется найти ее площадь.
Решение: зная длину грани, можно найти ее площадь:
S = 11² = 121 см²
Ответ: площадь грани куба с ребром 11 см равна 121 см²
Обратите внимание
Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб – это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр – это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т.п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы – баррель (1м³ = 6.29 баррелей)
Полезный совет
Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a²;
Объем: V = 6*a³;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((√3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*√3
Источники:
- площадь куба если ребра равны 11 см
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Загрузить PDF
Загрузить PDF
Площадь поверхности – это суммарная площадь всех поверхностей, которые составляют объемную фигуру. Площадь поверхности является числовой характеристикой поверхности.[1]
Вычислить площадь поверхности объемной (трехмерной) фигуры довольно просто, если знать соответствующую формулу. Существует определенная формула для каждой фигуры, поэтому сначала нужно определить, какая фигура дана. Чтобы быстро вычислять площадь поверхности, запомните соответствующие формулы для разных фигур. В данной статье рассматриваются наиболее распространенные фигуры.
-
1
Запишите формулу для вычисления площади поверхности куба. У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a2, где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности (SA) куба: SA = 6а2, где а – ребро куба (сторона квадрата).[2]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте ребро куба. Ребра куба равны, поэтому можно измерить только одно (любое) ребро. Ребро измерьте с помощью линейки (или рулетки). Обратите внимание на используемые единицы измерения.
- Запишите значение, обозначив его через а.
- Например: а = 2 см
-
3
Значение а возведите в квадрат. То есть возведите в квадрат длину ребра куба. Для этого умножьте значение на себя. Если вы только приступили к изучению формул с квадратами, запишите формулу так: SA = 6*а*а.
- Сейчас вы вычислили значение площади одной из граней куба.
- Например: а = 2 см
- a2 = 2 х 2 = 4 см2
-
4
Вычисленное значение умножьте на шесть. Помните, что у куба шесть равных граней. Вычислив площадь одной из граней, умножьте полученное значение на 6, чтобы включить все грани куба.
- Это последний шаг в процессе вычисления площади поверхности куба.
- Например: а 2 = 4 см2
- SA = 6 х а2 = 6 х 4 = 24 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности прямоугольной призмы. У прямоугольной призмы шесть граней, причем равными являются только противоположные грани.[3]
Поэтому формула для вычисления площади поверхности прямоугольной призмы включает значения трех разных ребер: SA = 2ab + 2bc + 2ac.- Здесь а – ширина, b – высота, с – длина призмы.
- Если проанализировать формулу, можно понять, что она суммирует площади всех граней.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения высоты, ширины и длины призмы. Три ребра не являются равными, поэтому нужно выполнить три измерения. Измерьте соответствующие ребра с помощью линейки (или рулетки). Ребра измеряйте в одной единице измерения.
- Измерьте длину грани, которая лежит в основании призмы; длину обозначьте через с.
- Например: с = 5 см
- Измерьте ширину грани, которая лежит в основании призмы; ширину обозначьте через а.
- Например: а = 2 см
- Измерьте высоту призмы; высоту обозначьте через b.
- Например: b = 3 см
-
3
Вычислите площадь одной грани призмы, а затем полученное значение умножьте на два. Помните, что у прямоугольной призмы шесть граней, причем равными являются только противоположные грани. Умножьте длину на высоту (с на а), чтобы найти площадь одной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[4]
- Например: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 см2
-
4
Вычислите площадь другой грани призмы, а затем полученное значение умножьте на два. Умножьте ширину на высоту (а на b), чтобы найти площадь другой грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[5]
- Например: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 см2
-
5
Вычислите площадь фронтальной грани, а затем полученное значение умножьте на два. Умножьте длину на ширину (с на b), чтобы найти площадь фронтальной грани. Затем полученное значение умножьте на 2, чтобы включить вторую (противоположную и равную) грань.[6]
- Например: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 см2
-
6
Сложите три значения. Так как площадь поверхности – это суммарная площадь всех граней фигуры, сложите найденные значения площадей отдельных граней. Вы получите площадь поверхности прямоугольной призмы.[7]
- Например: SA = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности треугольной призмы. Треугольная призма имеет две равные треугольные грани и три прямоугольные грани. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти площади всех граней и сложить их. Формула для вычисления площади поверхности треугольной призмы: SA = 2S + РH, где S – площадь треугольной грани, Р – периметр треугольной грани, H – высота призмы.[8]
- Здесь S – это площадь треугольника (треугольной грани), которая вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание).
- Р – периметр треугольника (треугольной грани), который равен сумме всех сторон треугольника.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Вычислите площадь треугольной грани и умножьте ее на два. Площадь треугольника вычисляется по формуле S = 1/2bh, где b – основание треугольника, h – высота треугольника (которая опущена на основание). Так как треугольная призма имеет две равные треугольные грани, эту формулу можно умножить на два. Поэтому, чтобы вычислить площади двух треугольных граней, просто перемножьте основание и высоту треугольника (b*h).[9]
- Основание треугольника b – это его нижняя сторона.
- Например: b = 4 см
- Высота треугольника h – это перпендикуляр, опущенный на основание из противоположной вершины.
- Например: h = 3 см
- Площадь двух треугольных граней равна: 2(1/2)b*h = b*h = 4*3 =12 см.
-
3
Измерьте каждую сторону треугольника и высоту призмы. Чтобы вычислить площадь поверхности треугольной призмы, нужно найти значение каждой стороны треугольника и высоты призмы. Высота призмы – это расстояние между треугольными гранями.
- Например: Н = 5 см
- Стороны треугольника – это три ребра одной (любой) из треугольных граней.
- Например: а = 2 см, b = 4 см, с = 6 см
-
4
Вычислите периметр треугольника. Для этого сложите все стороны треугольника: Р = а + b + с.
- Например: P = а + b + с = 2 + 4 + 6 = 12 см
-
5
Перемножьте периметр треугольной грани и высоту призмы. Помните, что высота призмы – это расстояние между треугольными гранями. Таким образом, Р умножьте на Н.
- Например: Р х Н = 12 х 5 = 60 см2
-
6
Сложите полученные значения. Чтобы найти площадь поверхности треугольной призмы, сложите два значения, вычисленные ранее.[10]
- Например: 2S + PH = 12 + 60 = 72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности шара. Шар имеет изогнутую поверхность, поэтому формула включает математическую константу π (число Пи). Чтобы вычислить площадь поверхности шара, воспользуйтесь формулой SA = 4π*r2.[11]
- Здесь r – радиус шара, π ≈ 3,14.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус шара. Радиус шара равен половине его диаметра, то есть половине отрезка, который проходит через центр шара и соединяет две точки, лежащие на его поверхности.[12]
- Например: r = 3 см
-
3
Радиус шара возведите в квадрат. Для этого умножьте значение радиуса (r) на себя. Помните, что формулу можно записать так: SA = 4π*r*r.[13]
- Например: r2 = r x r = 3 x 3 = 9 см2
-
4
Перемножьте квадрат радиуса и приблизительное значение числа Пи. Число Пи является математической константой, которая равна отношению длины окружности к ее диаметру.[14]
Это иррациональное число со множеством цифр после десятичной запятой. Зачастую число Пи округляется до 3,14. Квадрат радиуса умножьте на π (на 3,14), чтобы вычислить площадь круглого сечения шара. [15]
- Например: π*r2 = 3,14 x 9 = 28,26 см2
-
5
Полученное значение умножьте на четыре. Чтобы найти значение площади поверхности сферы, площадь круглого сечения умножьте на 4.[16]
- Например: 4π*r2 = 4 x 28,26 = 113,04 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности цилиндра. Цилиндрическая поверхность этой фигуры ограничена двумя круглыми параллельными плоскостями, которые называются основаниями. Формула для вычисления площади поверхности цилиндра: SA = 2π*r2 + 2π*rh, где r – радиус основания, h – высота цилиндра, π ≈ 3,14.[17]
- 2π*г2 – это площадь двух оснований, а 2πrh – это площадь цилиндрической поверхности.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту цилиндра. Радиус окружности равен половине ее диаметра, то есть половине отрезка, который проходит через центр окружности и соединяет две точки, лежащие на ней.[18]
Высота цилиндра – это расстояние между его основаниями. Измерьте и запишите радиус основания и высоту цилиндра.- Например: r = 3 см
- Например: h = 5 см
-
3
Вычислите площадь основания и умножьте ее на два. Чтобы найти площадь основания, воспользуйтесь формулой для вычисления площади круга: S = π*г2. Сначала радиус возведите в квадрат, а затем полученное значение умножьте на число Пи. Результат умножьте на два, чтобы учесть второе равное основание.[19]
- Например: площадь основания = π*r2 = 3,14 х 3 х 3 = 28,26 см2
- Например: 2π*r2 = 2 x 28,26 = 56,52 см2
-
4
Вычислите площадь цилиндрической поверхности. Для этого воспользуйтесь формулой S = 2π*rh, по которой можно найти площадь поверхности трубы. Здесь труба – это поверхность между двумя основаниями цилиндра. Перемножьте двойку, число Пи, радиус и высоту.[20]
- Например: 2π*rh = 2 x 3,14 x 3 x 5 = 94,2 см2
-
5
Сложите полученные значения. Сложите площади двух оснований и площадь цилиндрической поверхности (между двумя основаниями), чтобы вычислить общую площадь поверхности цилиндра. Обратите внимание, что при сложении этих величин получится исходная формула: SA = 2π*r2 + 2π*rh.[21]
- Например: 2π*r2 + 2π*rh = 56,52 + 94,2 = 150,72 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности квадратной пирамиды. Квадратная пирамида имеет одно квадратное основание и четыре треугольные грани. Помните, что площадь квадрата равна квадрату его стороны. Площадь треугольника равна 1/2sl (половина основания треугольника, умноженная на его высоту). Так как пирамида имеет четыре треугольные грани, нужно площадь треугольника умножить на 4. Таким образом, площадь поверхности квадратной пирамиды вычисляется по формуле: SA = s2 + 2sl.[22]
- В этой формуле s – ребро квадратной грани (сторона квадрата), l – апофема пирамиды.
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Найдите значения апофемы и ребра квадратной грани. Апофема (l) – это высота треугольной грани, то есть расстояние между основанием треугольника и его вершиной. Ребро квадратной грани (s) – это сторона квадрата. Помните, что у квадрата все стороны равны, поэтому измерьте любое ребро квадратной грани, а также измерьте апофему пирамиды.[23]
- Например: l = 3 см
- Например: s = 1 см
-
3
Найдите площадь квадратной грани. Для этого возведите в квадрат ребро этой грани (сторону квадрата), то есть умножьте значение s на себя.[24]
- Например: s2 = s х s = 1 х 1 = 1 см2
-
4
Вычислите общую площадь четырех треугольных граней. Вторая часть формулы включает суммарную площадь четырех треугольных граней. Согласно формуле 2ls, перемножьте 2, s и l. Так вы найдете суммарную площадь 4-х треугольных граней.[25]
- Например: 2 х s х l = 2 х 1 х 3 = 6 см2
-
5
Сложите полученные значения. Сложите площадь квадратной грани и общую площадь четырех треугольных граней, чтобы вычислить площадь поверхности пирамиды.[26]
- Например: s2 + 2sl = 1 + 6 = 7 см2
Реклама
-
1
Запишите формулу для вычисления площади поверхности конуса. Конус имеет круглое основание и закругленную боковую поверхность, которая сужается в вершине этой фигуры. Чтобы найти площадь поверхности конуса, нужно вычислить значения площади круглого основания и площади боковой поверхности, а затем сложить эти значения. Формула для вычисления площади поверхности конуса: SA = π*r2 + π*rl, где r – радиус круглого основания, l – образующая (расстояние между вершиной конуса и точкой, которая лежит на окружности круга), π ≈ 3,14.[27]
- Площадь поверхности измеряется в квадратных единицах, например, в мм2, см2, м2 и так далее.
-
2
Измерьте радиус основания и высоту конуса. Радиус – это отрезок, соединяющий центр круга и точку, которая лежит на его окружности. Высота – это расстояние между центром круга и высотой конуса.[28]
- Например: r = 2 см
- Например: h = 4 см
-
3
Найдите значение образующей конуса (l). Образующая конуса является гипотенузой треугольника, поэтому воспользуйтесь теоремой Пифагора, чтобы вычислить образующую: l = √(r2 + h2), где r – радиус круглого основания, h – высота конуса.[29]
- Например: l = √(r2 + h2) = √(2 х 2 + 4 х 4) = √(4 + 16) = √(20) = 4,47 см
-
4
Вычислите площадь круглого основания. Площадь круга вычисляется по формуле S = π*r2. Измерив радиус, возведите его в квадрат (умножьте r на себя), а затем квадрат радиуса умножьте на число Пи.[30]
- Например: π*r2 = 3,14 x 2 x 2 = 12,56 см2
-
5
Вычислите площадь боковой поверхности конуса. Сделайте это по формуле S = π*rl, где r – радиус круга, l – образующая, которая найдена ранее.[31]
- Например: π*rl = 3,14 x 2 x 4,47 = 28,07 см
-
6
Сложите полученные значения, чтобы найти площадь поверхности конуса. Площадь поверхности конуса равна сумме площади круглого основания и площади боковой поверхности конуса.[32]
- Например: π*r2 + π*rl = 12,56 + 28,07 = 40,63 см2
Реклама
Что вам понадобится
- Линейка
- Ручка или карандаш
- Бумага
Об этой статье
Эту страницу просматривали 69 399 раз.
Была ли эта статья полезной?
Как вычислить площадь грани
Плоский многоугольник, сторонами которого являются ребра объемной геометрической фигуры, принято называть гранью этого объекта. Сумма площадей всех граней составляет площадь поверхности объемной фигуры. А величину этого параметра для каждой грани можно рассчитать, если знать ее геометрические размеры или иметь достаточно данных об объемной фигуре в целом.
Если объемная фигура не имеет геометрически правильной формы, то составляющие ее грани могут иметь одинаковое количество сторон, но несовпадающие размеры. Поэтому площадь каждой из них придется вычислять раздельно, исходя из данных о длинах составляющих ее ребер. Если эта информация есть, используйте формулы для соответствующего многоугольника. Например, если есть возможность измерить длины всех ребер, образующих треугольную грань, то площадь ее вычисляйте по формуле Герона. Для этого сначала найдите половину от суммы длин всех сторон (полупериметр), затем последовательно отнимите от полупериметра длину каждой стороны. У вас получится четыре значения – полупериметр и его три уменьшенных на длины сторон варианта. Перемножьте все эти числа, а из результата извлеките квадратный корень. Для вычисления площади грани с другим количеством сторон может понадобиться еще более сложная формула или даже разбиение ее на несколько более простых многоугольников.
Вычисление площади граней объемной фигуры правильной формы значительно проще, так как ее все боковые поверхности имеют одинаковые размеры. Так, чтобы вычислить этот параметр для каждой из шести граней куба достаточно знать длины двух смежных ребер многогранника. Их произведение и даст величину площади любой из граней. Зная количество плоскостей, которыми образована объемная фигура правильной формы, площадь каждой из них можно рассчитать из общей площади поверхности – разделите эту величину на количество граней.
Некоторые многогранники хоть и не состоят из одинаковых граней, тем не менее называются правильными и позволяют использовать достаточно простые формулы расчета плоскостей, составляющих их поверхность. Это фигуры с центральной осью симметрии, в основании которых лежит правильный многоугольник – например, пирамида. Ее боковые грани имеют форму треугольников одинаковых размеров. Площадь каждой можно рассчитать, если известна длина стороны многоугольника, лежащего в основании объемной фигуры, и ее высота. Умножьте длину стороны на количество граней основания и высоту пирамиды, а полученную величину разделите пополам. Рассчитанное значение и будет площадью каждой боковой грани пирамиды.
Формулы?
Площадь поверхности куба равна сумме площадей шесть квадратов, которые и составляют поверхность куба.
Площадь каждого такого квадрата, которые являются гранями данного куба, вычисляются по формуле:
, где а – длина ребра квадрата.
Чтобы найти площадь всей поверхности квадрата, надо найти сумму площадей всех шести его граней или просто, умножить площадь одной из граней на 6.
Вот так можно вывести формулу вычисления площади поверхности куба:
модератор выбрал этот ответ лучшим
Турук Макто
[55.4K]
9 лет назад
Я формул не помню, если они специально какие-то есть. Но давайте по логике. Если сторона одна – это квадрат, то сторона умножается на сторону – это будет площадь квадрата. И таких квадратов шесть штук. Вот собственно и всё. Сторона в квадрате шесть раз! 6*а*а.
MarkTolkien
[85.2K]
9 лет назад
Для того, чтобы найти площадь поверхности куба, нужно вычислить площадь грани. Площадь одной грани – длина ребра в квадрате, то есть во второй степени. У куба шесть сторон (граней), поэтому площадь одной множим на 6.
Ракитин Сергей
[450K]
9 лет назад
У куба шесть граней, каждая из которых представляет собой квадрат. Если сторона куба равна a, то площадь его поверхности будет равна 6a^2. В справочниках эту формулу обычно не приводят в силу её очевидности.
Асюшка
[101K]
9 лет назад
Так как грани куба – это квадраты. И куб состоит из шести таких граней, то получается, что чтобы найти площадь поверхности куба, нам необходимо для начала найти площадь квадрата(грани куба) умножаем на 6 (6 граней). Ой, сейчас сама запутаюсь и Вас запутаю, проще, действительно, формулой записать:
S (площадь куба) = 6 * а2 (площадь одной грани – квадрата).
Медвед
[141K]
9 лет назад
Куб – это параллелепипед, у которого все стороны равны. Значит, каждая из граней куба является квадратом, и все эти квадраты равны между собой. Если обозначить сторону куба как Н, площадь одного квадрата будет (Н)в квадрате. Таких квадратов 6. Поэтому имеем формулу для определения поверхности куба S:
S=6x[(Н)в квадрате]
Samborskaya
[7K]
9 лет назад
Площадь поверхности куба складывается из всех площадей его сторон. Каждая сторона представляет из себя квадрат, а площадь квадрата равна произведению его сторон. Пусть сторона квадрата равна Х, тогда площадь всей поверхности куба вычисляется как S = 6 * X * X.
Любовь7800
[4K]
9 лет назад
И без формул даже можно, если нужно измерить все поверхности, то найти площать одной, умножив одну сторону на другую и потом умножить на шесть. Так ка у куда все стороны равны, то можно одну сторону умножить сразу на 12, так как граней 12.
Радуга-Весна
[50.4K]
9 лет назад
Площадь поверхности куба равняется шесть умножить на квадрат длины грани куба.
А вот и сама формула площади куба
S = 6* a2
S – это площадь куба,
a – это длина грани куба.
Как видно площадь куба рассчитывается совсем просто.
Solnce lychik
[40.9K]
9 лет назад
Эту площадь учили еще в школе. А формула выглядит так:
s=6*a2
где s-площадь куба
a-длина грани
Если честно без интернета я бы это и не вспомнила.
Да все что учила в школе со временем забывается. А вспомнить очень сложно.
Знаете ответ?
Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).
Рисунок 1
Определение
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.
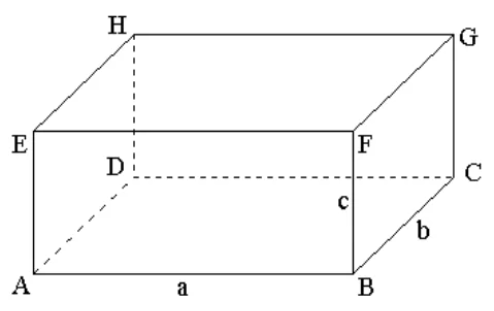
Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.
У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.
Рисунок 2
Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.
Длина, ширина, высота
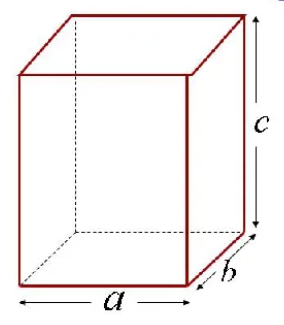
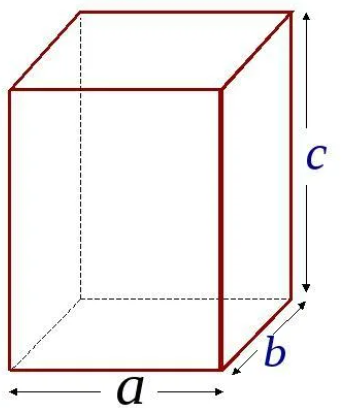
Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.
Рисунок 3
Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.
Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.
Куб
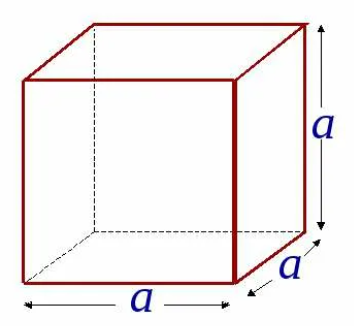
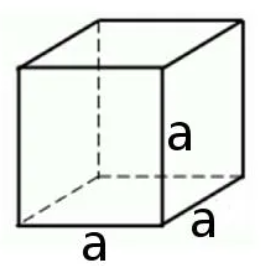
Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).
Рисунок 4
Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a2. Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a2
Объем прямоугольного параллелепипеда
Рисунок 5
С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.
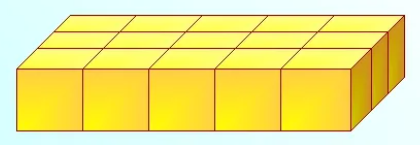
Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.
Рисунок 6
За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.
Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм3; с ребром 1 см – кубическим сантиметром (см3) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.
Формула объема прямоугольного параллелепипеда
Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.
Рисунок 7
Объем куба
Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:
V=a3
Рисунок 8
Пирамида
Рисунок 9
Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).
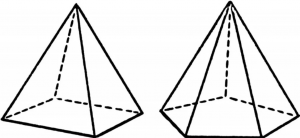
Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).
Рисунок 10
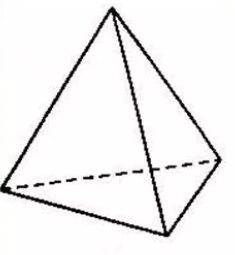
Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.
Рисунок 11
Даниил Романович | Просмотров: 913