Как найти плошадь осевого сечения конуса

Осевым сечением конуса в треугольнике, является не что иное, как произведение его длины и высоты. То есть по сути, это все внутренне пространство, которое есть внутри треугольника, а так как его образует как длина этого самого треугольника, так и его радиус, то для того что бы его найти, нужно две эти величины, просто между собой, перемножить. автор вопроса выбрал этот ответ лучшим Степа­н-16 [34.5K] 5 лет назад  Осевым сечением конуса является равнобедренный треугольник. Соответственно, площадь осевого сечения будет определяться формулой площади треугольника и равна половине произведения основания треугольника (или диаметра окружности – основания конуса) на высоту треугольника (или конуса). Если проще, то: произведению радиуса основания конуса на его высоту. Ankla­v [4.4K] 8 лет назад  Вообразите себе конус и разделите его на две части сверху вниз. Это будет треугольник . А формулу, как найти площади его, вы знаете: S = 1/2D h = R * h На самом деле, нахождение площади сечения в случаях в стереометрии сводится к понятиям обычной геометрии на плоскости Ксарф­акс [156K] 6 лет назад  Определение из курса стереометрии: Осевое сечение – это сечение трёхмерной фигуры плоскостью, которая проходит через ось этой фигуры. Для конуса осевым сечением будут являться треугольник. Таким образом, для нахождения площади осевого сечения конуса необходимо найти площадь данного треугольника. Площадь треугольника равна половине произведения основания на высоту, проведённую к данному основанию. Высота треугольника будет совпадать с высотой конуса, она равна h. Основание треугольника будет равно диаметру окружности d (окружность является основанием конуса). Таким образом, S = 0,5*d*h. Так как половина диаметра окружности – это радиус, то формулу можно переписать в следующем виде: Sсеч = R*h. Пчела Жужа [77.9K] 5 лет назад  Площадь осевого сечения конуса можно высчитать, применив формулу S=1/2d*h=Rh, где S является площадью осевого сечения, R является радиусом, d является диаметром конуса, а h – это высота конуса. Стоит отметить, что осевым сечением является треугольник. Площадь осевого сечения конуса вычисляется по формуле: S=1/2*(h*2r),где h -это высота,r-это радиус основания.Например.если высота конуса равна 5 см, а радиус основания равен 2,5 см, то площадь осевого сечения будет равна S=0.5*(5*2*2.5)=12.5 cm Антон­75 [206] 8 лет назад  Осевое сечение конуса – это треугольник.Следовательно, площадь осевого сечения конуса равна произведению высоты конуса на радиус основания. S=h*r Oleg7­4 [202K] 8 лет назад  При осевом сечении конуса плоскость проходит через вершину данного конуса , а самим сечением получается треугольник. Площадью такого сечения является половина диаметра или радиуса, умноженного на высоту. То есть формула вычисления такой площади выглядит так : S = 1/2D h = R h где D – это диаметр конуса ( основания ), R – радиус основания, а h – это высота конуса и треугольника, соответственно. morel­juba [62.5K] 6 лет назад  В первую очередь хочу отметить тот факт, что осевое сечение конуса представляет собой треугольник. Этот факт означает что от нас требуется найти площадь данного треугольника. Найдём площадь вот по этой формуле: В данной формуле диаметр конуса – это D. Радиус основания – это R, а высотой конуса здесь является h. timur­ovec [273K] 8 лет назад  Для ответа необходимо хорошее пространственное представление. Если конус разделить от вершины до средины основания , мы получим фигуру треугольника. А площадь треугольника высчитывается произведением высоты на длину нижней стороны , деленную на два , в данном случае это радиус. Ksyus­ha26 [26.8K] 8 лет назад  Надо сказать, что сечение представляет собой ни что иное, как треугольник. То есть найти площадь осевого сечения конуса можно найти с помощью следующей формулы: S=1/2d*h=Rh. D признается диаметром конуса, R признается радиусом основания, h является высотой конуса Знаете ответ?

Площадь сечения конуса. Для вас представлена очередная статья с конусами. На момент написания этой статьи на блоге решены все примеры (прототипы) заданий с конусами, которые возможны на экзамене. Процесс решения несложен (1-2 действия), при определённой практике решаются устно. Нужно знать понятие образующей, об этом информация в этой статье. Так же необходимо понимать как образуются сечения конуса.

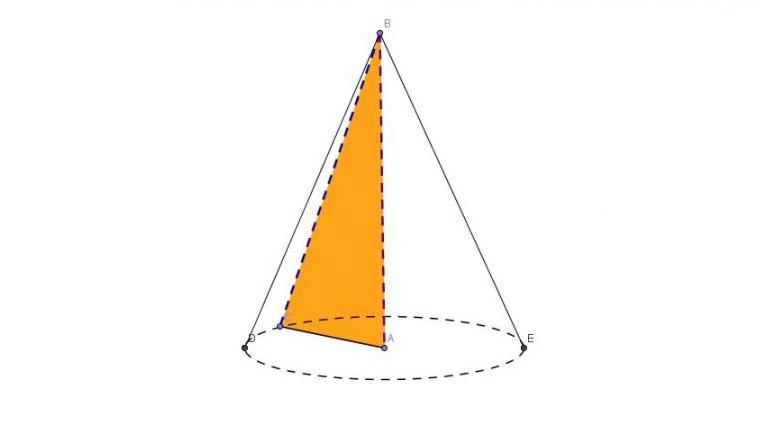
1. Если плоскость проходит через вершину конуса, то сечением является треугольник.

*Если плоскость проходит через ось конуса, то сечением является равнобедренный треугольник, высота которого равна высоте конуса, а основание на которое опущена эта высота равна диаметру основания конуса.

2. Если плоскость проходит перпендикулярно оси конуса, то сечением является круг.

Особенностью данных заданий является то, что применяется формула площади треугольника, здесь она первая. Формулы периодически повторяйте. Рассмотрим задачи:

324453. Площадь основания конуса равна 16Пи, высота равна 6. Найдите площадь осевого сечения конуса.

Осевым сечением конуса является треугольник с основанием равным диаметру основания конуса и высотой равной высоте конуса. Обозначим диаметр как D, высоту как Н, запишем формулу площади треугольника:

Высота известна, вычислим диаметр. Используем формулу площади круга:

Значит диаметр будет равен 8. Вычисляем площадь сечения:

Ответ: 24

324454. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Сечением является круг. Необходимо найти площадь этого круга.

Построим осевое сечение:

Рассмотрим треугольники AKL и AOC – они подобны. Известно, что в подобных фигурах отношения соответствующих элементов равны. Мы рассмотрим отношения высот и катетов (радиусов):

OC  это радиус основания, его можно найти:

Значит

Теперь можем вычислить площадь сечения:

*Это алгебраический способ вычисления без использования свойства подобных тел, касающегося их площади. Можно было рассудить так:

Два конуса (исходный и отсечённый) подобны, значит пощади их оснований являются подобными фигурами. Для площадей подобных фигур существует зависимость:

Коэффициент подобия в данном случае равен 1/3 (высота исходного конуса равна 9, отсечённого 3), 3/9=1/3.

Таким образом, площадь основания полученного конуса равна:

Ответ: 2

323455. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R.

Найдём диаметр основания и используя формулу площади треугольника вычислим площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 48

Диаметр основания конуса равен 40, а длина образующей — 25. Найдите площадь осевого сечения этого конуса.

Пусть образующая это L, высота это H, радиус основания это R. 

Радиус основания равен половине диаметра, то есть 20.

Вычислим высоту и далее используя формулу площади треугольника найдём искомую площадь. По теореме Пифагора:

Вычисляем площадь сечения:

Ответ: 300

На этом всё. Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Круглый конус в геометрии является симметричной пространственной фигурой, имеющей ось вращения. Одной из важных его характеристик является площадь сечения осевого. В данной статье приведем формулу площади сечения осевого конуса прямого с круглым основанием и усеченного.

О какой фигуре будет идти речь?

Круглый конус – это фигура, которую можно получить следующим образом. Необходимо взять треугольник с углом прямым и его вокруг одного из катетов вращать. Тогда получится показанная ниже объемная фигура.

Отрезок AC на рисунке называется радиусом основания, который “рисует” при вращении с центром в точке A круг. Катет AB – это высота конуса. Очевидно, что отрезок AB перпендикулярен основанию и является частью оси вращения фигуры. Точка B – это высота рассматриваемой фигуры. Отрезок BE называется образующей, или генератрисой конуса. Совокупность всех генератрис образует боковую поверхность конуса. Она является конической. Ограничивающая основание окружность называется направляющей, или директрисой конуса.

Поскольку генератриса, радиус и высота являются гипотенузой и катетами рассмотренного прямоугольного треугольника, то для них можно записать формулу:

g² = r² + h²

Здесь g – генератриса, r – радиус, h – высота.

Осевое сечение конуса и его площадь

Чтобы записать для конуса формулу площади сечения осевого, сначала следует познакомиться с самим сечением. Оно получается так: нужно взять секущую плоскость, расположить ее параллельно оси конуса. Затем необходимо разрезать конус плоскостью на две одинаковые части таким образом, чтобы в плоскость сечения попала вершина фигуры.

Несложно себе представить, что в результате описанной операции получится равнобедренный треугольник. Равные стороны треугольника будут такие же, как длины генератрис. А третья сторона будет равна диаметру основания.

Формула площади осевого сечения конуса (фото см. выше) не отличается сложностью. Она соответствует формуле расчета этой величины для описанного треугольника. Поскольку у треугольника площадь равна произведению основания на высоту, которое следует поделить пополам, то искомое равенство для осевого сечения примет вид:

S = h*r

Эта формула говорит о том, что S в два раза больше площади прямоугольного треугольника, вращением которого был получен конус.

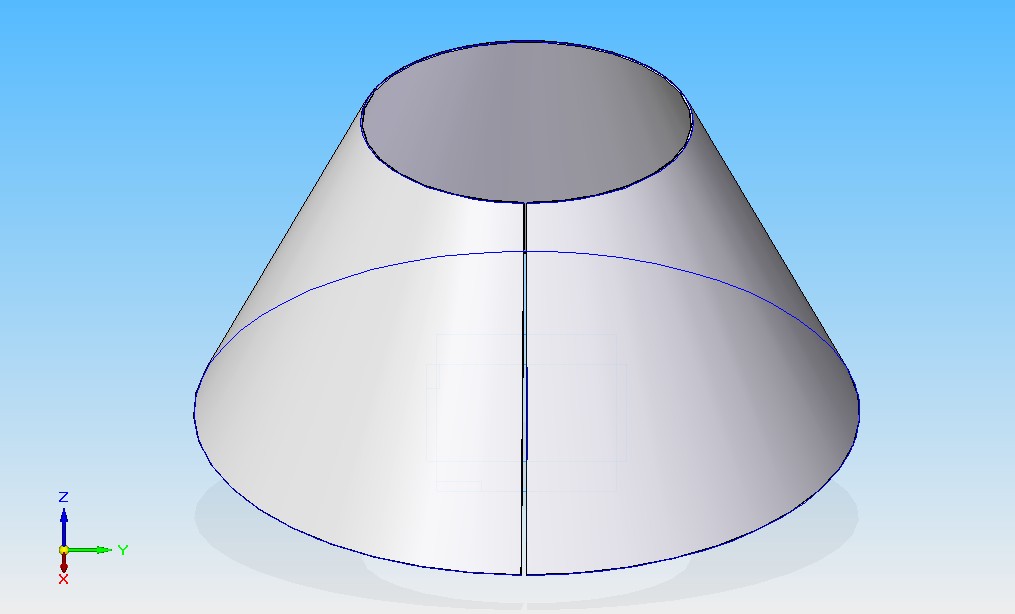
Усеченный конус и его осевое сечение

Усеченный конус получается из обычного при помощи секущей плоскости, которая параллельна его основанию. Полученная при этом фигура под плоскостью будет усеченным конусом. Он показан на рисунке.

Помимо боковой поверхности, эта фигура состоит из двух оснований, которые представляют собой большой и малый круги. Обозначим их радиусы как r₁ и r₂. Расстояние между основаниями называется высотой, обозначим ее буквой h.

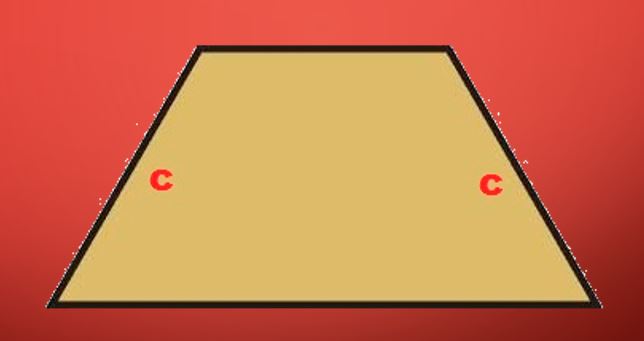
Осевое сечение рассматриваемого конуса будет четырехугольником, две стороны которого являются образующими. А две другие стороны будут параллельны друг другу и равны 2*r₁ и 2*r₂ соответственно. Этот четырехугольник будет равнобедренной трапецией, которая показана на рисунке ниже.

Этот факт позволяет использовать выражение для трапеции, чтобы записать формулу площади сечения усеченного осевого конуса . Она примет вид:

S = (2*r₁ + 2*r₂)/2*h = h*(r₁ + r₂)

То есть площадь S равна произведению суммы радиусов оснований усеченного конуса на его высоту.

Для решения геометрических задач также может потребоваться формула связи между генератрисой фигуры и ее параметрами r₁, r₂ и h. Соответствующее выражение приобретает вид:

g² = h² + (r₁ – r₂)²

Получить ее достаточно просто самостоятельно, если рассмотреть прямоугольный треугольник внутри конуса, построенный на сторонах g, h и (r₁ – r₂).

Задача на определение площади сечения осевого конуса усеченного

Покажем, как находить площадь осевого сечения на примере усеченного конуса.

Известно, что высота указанной фигуры составляет 10 см. Также известно, что для конуса осевого сечения площадь равна разности площадей оснований. Зная, что диаметры оснований отличаются ровно в два раза, необходимо найти площадь этого сечения по оси.

В соответствии с условием задачи можно записать два уравнения:

r₁ = 2*r₂;

h*(r₁ + r₂) = pi*(r₁² – r₂²)

Значение высоты известно из условия. Таким образом, мы имеем 2 равенства и 2 неизвестные величины. Решаем эту систему:

h*(2*r₂ + r₂) = pi*((2*r₂) ² – r₂²) =>

3*pi*r₂² – 3*h*r₂ = 0

Мы получили неполное квадратное уравнение, которое следует решить относительно переменной r₂. Уравнение имеет 2 корня, но решение r₂ = 0 не является физическим, поэтому запишем только одно единственное значение для малого радиуса:

r₂ = h/pi

Тогда большой радиус r₁ будет равен:

r₁ = 2*h/pi

Подставляя эти равенства в формулу площади осевого сечения конуса, получаем:

S = h*(r₁ + r₂) = 3*h²/pi

Подставляем численное значение h и записываем ответ: S ≈ 95,54 см².

Как найти площадь осевого сечения конуса

Конус представляет собой геометрическое тело, основание которого представляет собой круг, а боковая поверхности — все отрезки, проведенные из точки, находящейся вне плоскости основания, к этому основанию. Прямой конус, который обычно рассматривается в школьном курсе геометрии, можно представить как тело, образованное вращением прямоугольного треугольника вокруг одного из катетов. Перпендикулярным сечением конуса является плоскость, проходящая через его вершину перпендикулярно основанию.

Вам понадобится

• Чертеж конуса с заданными параметрами
• Линейка
• Карандаш
• Математические формулы и определения
• Высота конуса
• Радиус окружности основания конуса
• Формула площади треугольника

Инструкция

Начертите конус с заданными параметрами. Обозначьте центр окружности как О, а вершину конуса — как P. Вам необходимо знать радиус основания и высоту конуса. Вспомните свойства высоты конуса. Она представляет собой перпендикуляр, проведенный из вершины конуса к его основанию. Точка пересечения высоты конуса с плоскостью основания у прямого конуса совпадает с центром окружности основания. Постройте осевое сечение конуса. Оно образовано диаметром основания и образующими конуса, которые проходят через точки пересечения диаметра с окружностью. Обозначьте полученные точки как А и В.

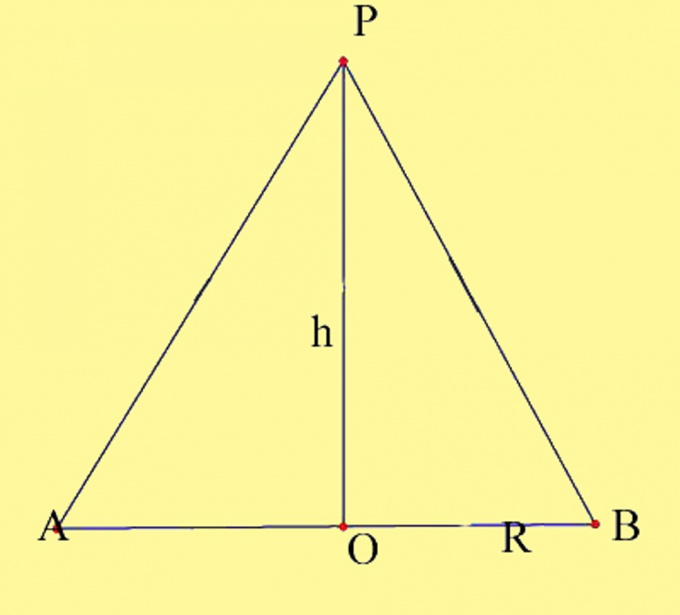
Осевое сечение образовано двумя прямоугольными треугольниками, лежащими в одной плоскости и имеющими один общий катет. Вычислить площадь осевого сечения можно двумя способами. Первый способ — найти площади получившихся треугольников и сложить их вместе. Это наиболее наглядный способ, но по сути он ничем не отличается от классического вычисления площади равнобедренного треугольника. Итак, у вас получилось 2 прямоугольных треугольника, общим катетом которых является высота конуса h, вторыми катетами — радиусы окружности основания R, а гипотенузами — образующие конуса. Поскольку все три стороны этих треугольников равны между собой, то и сами треугольники тоже получились равными, согласно третьему свойству равенства треугольников. Площадь прямоугольного треугольника равна половине произведения его катетов, то есть S=1/2Rh. Площадь двух треугольников соответственно будет равна произведению радиуса окружности основания на высоту, S=Rh.

Осевое сечение чаще всего рассматривают как равнобедренный треугольник, высотой которого является высота конуса. В данном случае это треугольник АPВ, основание которого равно диаметру окружности основания конуса D, а высота равна высоте конуса h. Площадь его вычисляется по классической формуле площади треугольника, то есть в итоге получаем ту же самую формулу S = 1/2Dh = Rh, где S – площадь равнобедренного треугольника, R – радиус окружности основания, а h — высота треугольника, являющаяся одновременно и высотой конуса.

Полезный совет

Площадь осевого сечения конуса вычисляется по формуле площади трапеции. В этом случае необходимо знать оба радиуса оснований, высоту и серединную линию.

Источники:

• Урок Тема “Сечения конуса

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?