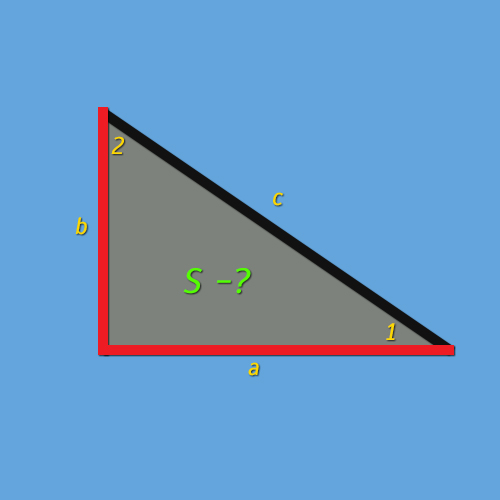
Прямоугольный треугольник – это замечательный пример геометрических фигур, которые встречаются во всех аспектах нашей жизни, от строительства до дизайна и даже в математическом контексте. В этой статье мы рассмотрим один из ключевых аспектов прямоугольного треугольника – площадь. Наши расчеты помогут вам не тольily*/em> узнать, как найти ее, но и разобраться в сути геометрии.
Итак, что такое площадь? Площадь – это измерение крупного пространства, занимаемого фигурой на плоской поверхности. В случае прямоугольного треугольника, площадь описывает собой пространство, занимаемое тремя отрезками, которые создают треугольник. Для того, чтобы найти площадь треугольника, вам нужно знать длины двух сторон и угла между ними.
Важно отметить, что прямоугольный треугольник имеет один прямой угол. Подобный треугольник уникален тем, что использует теорему Пифагора для определения третьей стороны. Что означает, что если две стороны названы a и b, а третья сторона названа c, тогда формула Пифагора будет следующей:
a^2 + b^2 = c^2
Этот факт, наряду со знанием площади треугольника, позволит вам получить глубокое понимание геометрии и применять эту информацию в реальной жизни!
Основные концепции и правила
При поиске площади в прямоугольном треугольнике необходимо знать несколько важных концепций и правил.
Понятия “прямоугольный треугольник”

Прямоугольный треугольник – это геометрическая фигура с тремя сторонами, имеющая один прямой угол (90°). Другие два угла у такого треугольника называют прямоугольными.
Правило Пифагора
Основное правило для вычисления сторон прямоугольного треугольника – Теорема Пифагора. Согласно ему, в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов других двух сторон:
A² + B² = C²
Где C – гипотенуза, а A и B – катеты треугольника.
- Если нужно найти сторону c, можно разделить на 2 повышенную в квадрат площадь треугольника и найти квадратный корень:
- Если нужно найти сторону a или b перейти от главного положения пифагора к данному персонажу и разделить на квадратный корень.
Процедура вычисления площади прямоугольного треугольника
Теперь, когда вы знаете основные термины и правила, вы можете продолжить и определите площадь прямоугольного треугольника. Для этого используйте формулу площади:
Площадь = 1/2 * основание * высота
Основание – это сторона какого-либо треугольника, а высота – отрезок, проведенный из противоположного вершины этой стороны к ней перпендикулярно.
Правила для вычисления площади с помощью теоремы Пифагора
- Вычислите стороны прямоугольного треугольника с помощью теоремы Пифагора. Используйте только два катета и добавьте их квадраты и уже по полученной формуле и получите гипотенузу.
- Получите площадь используя формулу: Площадь = 1/2 * основание * высота.
Понятие прямоугольного треугольника
Определение прямоугольного треугольника

Один из трёх углов в таком треугольнике прямой, а остальные два – острыми. Это означает, что сумма углов в прямоугольном треугольнике будет равна 180 градусов. Из этого следует, что если руководствуясь этими условиями, можно определить прямоугольный треугольник среди других видов треугольников.
Свойства
- Один угол равен 90 градусам, а остальные два – острыми (меньше 90 градусов).
- У периметра прямоугольного треугольника нет общего знаменателя, так что для составления полноценного периметра треугольника будут использованы все стороны: периметр = (а + b + с), где а, b и с – это стороны треугольника.
- Площадь прямоугольного треугольника определяется с помощью формулы площади: площадь = ½ \* основание \* высота.
- Формулы справедливы и для других типов треугольников, однако для прямоугольных треугольников они также могут быть имплементированы с данными об определении гипотенузы.
Свойства катетов и гипотенузы
Для понимания базовых свойств катетов и гипотенузы в прямоугольном треугольнике, давайте вспомним основные определения каждого из этих элементов.
- Катеты – это два катета – стороны прямоугольного треугольника, прилегающие к прямому углу.
- Гипотенуза – гипотенуза является самым длинным ребром прямоугольного треугольника, противолежащим прямому углу.
Следующие свойства более подробны и ближе к решению получение площади в прямоугольном треугольнике:
Свойства катетов
Как правило, катеты имеют два важных свойства:
- Сумма квадратов катетов равна квадрату гипотенузы (по теореме Пифагора). В математической форме это будет выглядеть следующим образом: a^2 + b^2 = c^2, где a и b являются катетами, а c является гипотенузой.
- Катеты являются сторонами, противолежащими углам, которые вместе составляют прямой угол. Обратите внимание, что это свойство не работает для непрямоугольных треугольников.
Свойства гипотенузы
Гипотенуза обладает следующими двумя основными свойствами:
- Гипотенуза всегда является самой длинной стороной треугольника. Это означает, что длина гипотенузы в любом прямоугольном треугольнике превышает длину любых двух других сторон.
- Гипотенуза противоположна прямому углу. Взгляните на прямоугольный треугольник. Видите прямой угол на стене? Гипотенуза – это длина от твоего носа до края стены.
Когда вы понимаете основные составляющие треугольника, образование площади становится более простым, используя теорему Пифагора или другие аналогичные уравнения. Эти свойства, следовательно, очень важны для понимания концепций треугольников в математике.
Термины в геометрии и их значение
Основные определения геометрии
Геометрия, как самостоятельный раздел математики, посвящает свое внимание выяснению свойств и характеристик различных пространств и форм, определению делений, отношений этих многообразий. Также стоит выделить следующие определения, воспринятые как таковые основные:
- Геометрическая фигура – форма прямое представительство развёртывает идеи об анализе геометрических объектов. Все представляемые строго в этой форме линии, точки и плоскости.
- Геометрический объект – человек самостоятельно определяет элемент фигурой или как тело, или как пространство, с помощью геометрических констант измерильных величин, например, арифметические и доступные измерительные способы линейные, площади, объемов и окружённость.
Связанные термины

В творении математических понятий геометрия включает в себя следующие основные термины:
- Точка – это строгого определения точек (например нулевая величина, абсолютный ноль), которые представлены в качестве «непротяженности» не имеют. Но могут определять как определенный элемент пространства или точки на координатной оси, имеют координаты, которой в любой математической модели имеется.
- Прямая – это неизменное изложение через себя, специфицированное единственным свойством, которое вы пытаетесь переместить и вращать фигуру, а свойство не поменяется только мировая бесконечность, не двух- и не трех-мерных пространствах.
- Площадь треугольника – это некоторая сущность, которая характеризует однообразие геометрических предмета, основанная на трёх точке, соединивших линиям из первоначальной точки. Цель площади – результат произведения половины произведения значений двух катетов классического прямоугольного треугольника.
По своему виду и разным представлению геометрические объекты имеют разнообразные способы действий и свойственного описание свойств.
Методы нахождения площади
Метод нахождения площади на основе теоремы Пифагора
Данный метод основывается на теореме Пифагора, которая формулируется следующим образом: если в прямоугольном треугольнике длины катетов равны a и b, длина гипотенузы равна c, то a²+b²=c². Отсюда следует, что площадь прямоугольного треугольника равна половине произведения длин катетов, то есть (a*b)/2.
Метод нахождения площади на основе гипотенузы
Если известны длины катетов прямоугольного треугольника a и b, а также длина гипотенузы c, то площадь треугольника можно найти по формуле ((a*b)/2). Этот метод аналогичен предыдущему, но имеет некоторые отличия в условиях применения.
Таблица методов нахождения площади
| Метод | Условия | Формула |
|---|---|---|
| У赛的Пифагорон | a и b – длины катетов | (a*b) / 2 |
| Гипотенузаиичный | a, b – длины катетов, c – гипотенуза | ((a*b) / 2) |
Однако особенность данных методов заключается в том, что площадь прямоугольного треугольника может быть найдена только при условии, что величины катетов известны. В других случаях может требоваться применение других методов.
Формула Герона
Оригинальный метод Герона
Герон – известный древнегреческий математик и астроном, живший в I веке н. э. Он разработал оригинальный метод нахождения площади треугольника, который основывается на теореме Пифагора и на том факте, что квадратный корень из произведения двух переменных равен квадратному корню из суммы квадратов этих переменных.
Свойства формулы Герона

Один из главных преимуществ формулы Герона заключается в том, что она работает для любых треугольников, включая тупоугольные, остроугольные и прямоугольные.
В отличие от других формул, Герон не требует знания углов или высот треугольника. Все, что нужно знать, – это длины трех сторон, что делает ее особенно удобной и эффективной для решения разных задач.
Однако следует учитывать, что формулу Герона можно применять только в случае, когда все стороны треугольника могут образовать треугольник в принципе. Когда хотя бы одна сторона треугольника превышает сумму других двух, формально говоря, треугольника не существует, и формула Герона ни к чему не приближает.
Применение формулы Герона в прямоугольном треугольнике
Несмотря на то что формула Герона может использоваться для любых треугольников, для прямоугольного треугольника существует более простой способ найти площадь.
В прямоугольном треугольнике площадь равна половине произведения длины двух краев, образующих прямой угол. Это легко понять, если представить прямоугольный треугольник как состоящий из двух таких треугольников, возможно, неравных по размеру. В некоторых случаях формула Герона может быть полезна для нахождения площади треугольника, тем не менее, есть более простые и быстрые способы для разных типов треугольников.
Практическое применение формулы Герона

История формулы Герона
Формула Герона была названа в честь древнегреческого математика Герона из Александрии, соавтора “Метрики”, известной книги математических методов измерения и геометрии. Хотя считается, что формула известна задолго до Герона, это она сохранила его имя до наших дней.
Использование формулы Герона
Формула Герона звучит так: площадь прямоугольного треугольника, зная длины его сторон a, b и c (где c – это гипотенуза), равна квадратному кореню из ((a + b + c) * (-a + b + c) * (a – b + c) * (a + b – c)) / 16.
Благодаря удобству формулы Герона, ее легко использовать во многих практических задачах: от измерения местности и полей до решения геометрических задач, выполнения строительных работ и даже в космонавтике при планировании орбитальных манёвров с помощью солнечных панелей.
Необходимо учитывать, что при работе со сложными геометрическими задачами, существуют и другие формулы и методы решения проблем связанных с нахождением площади не только прямоугольных треугольников, но и других фигур.
Формула Герона доказала свою жизнеспособность в решении многих геометрических задач и обеспечивает хорошие результаты при правильном ее применении. Ее универсальность позволяет включать формулу Герона в состав единых решающих модулей как для стандартных, так и для сложных проектов, где требуются идеи и методология, основанные на геометрии и мерно/измерительных технологиих.
Другие способы определения площади
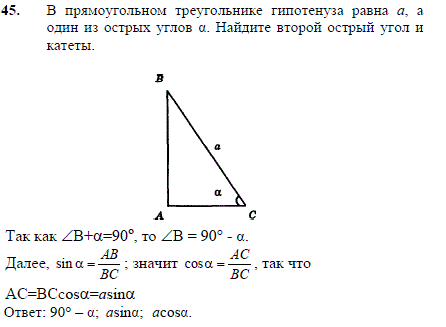
Площадь прямоугольного треугольника можно определить не только через основу и высоту, но и с помощью других методов. Мы рассмотрим некоторые из них.
1. Метод Герона: Площадь треугольника можно получить через его стороны с помощью формулы Герона. Если известны длины всех трех сторон треугольника, можно использовать следующую формулу:
Площадь = квадратный корень из((a + b + c) / 2 * ((a + b + c) / 2 – a) * ((a + b + c) / 2 – b) * ((a + b + c) / 2 – c))
где a, b и c – это длины сторон треугольника.
2. Использование теоремы Пифагора: Если у нас имеем прямоугольный треугольник, мы можем также использовать теорему Пифагора для нахождения третьей стороны, которая будет высотой, и использовать это значение для нахождения площади по формуле площади треугольника (1/2 * основание * высота).
Данный метод особенно удобен, когда три точки треугольника значения пространства имеют координаты (x1, y1), (x2, y2) и (x3, y3). В этом случае, можно найти стороны треугольника с помощью разности координат, а потом найти площадь через теорему Пифагора и формулу площади.
3. Использование формулы Брамагупти: Если известны длины американских сторон треугольника и его медиан (сторон, соединяющих середину основания с вершиной), то можно использовать формулу Брамагупти для нахождения площади:
Площадь = 1/2 * медиана * медиана
Стоит отметить, что эта формула работает только для треугольников с одинаковой медианой и серединным перпендикуляром.
Как видно, существует несколько способов определения площади прямоугольного треугольника. В зависимости от данных, доступных для вас и характера проблемы, вы можете выбрать наиболее подходящий подход для решения задачи.
Вопрос-ответ:
Что такое прямоугольный треугольник?
Прямоугольный треугольник – это треугольник, у которого один угол прямой (то есть равен 90 градусам). В таком треугольнике можно найти гипотенузу – наибольшую сторону, противоположную прямому углу, и использовать теорему Пифагора для решения других задач.
Каким образом можно найти площадь в прямоугольном треугольнике?
Площадь прямоугольного треугольника (и любого треугольника) вычисляется с помощью формулы: половина удвоенного произведения основания и высоты, умноженных друг на друга. Это выглядит так: площадь = (полуоснование * высота) / 2.
Могут ли мы использовать формулу Пифагора для нахождения площади прямоугольного треугольника?
Теорема Пифагора используется для нахождения гипотенузы в прямоугольном треугольнике с использованием катетов, но не для нахождения площади. Для этого вам нужно использовать формулу для определённой площади прямоугольного треугольника.
Как найти длину стороны, стоящей напротив прямого угла в прямоугольном треугольнике?
Для нахождения сторон стоящих напротив прямого угла используйте теорему Пифагора. Если a и b – катеты треугольника, а гипотенуза обозначается как c, тогда c² = a² + b². Это позволит вам найти сторону, стоящую напротив прямого угла, иначе именуемую гипотенузой.