Как найти площадь 8 гранника

Восьмиугольник – это геометрическая фигура из мира многоугольников; восьмиугольник имеет 8 сторон и 8
углов или вершин. Правильный многоугольник представляет собой выпуклый многоугольник с равенством
всех сторон и всех углов при вершинах. Следовательно, правильный восьмиугольник – это выпуклый
восьмиугольник, с равенством 8 сторон и 8 углов при вершинах. Другое название фигуры – октагон, от
латинского octo», что означает «восемь». Иногда требуется узнать площадь геометрической фигуры по
некоторым ее известным размерам, например, с целью узнать расход материала на изготовление, заливку,
окраску; или же массу в отсутствие весов при известной толщине многоугольной плитки и плотности
материала.

Для вычисления площади октагона необходимо знать его периметр, который в данном случае равен сумме
длин его 8 сторон (восьмикратной длине одной стороны), и апофему. В планиметрии апофемой называется
длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон.

При известной апофеме площадь правильного многоугольника равна произведению периметра на апофему,
деленному на 2 (в пределе эта формула справедлива даже для круга, где «апофема» равна радиусу).
Поскольку периметр в рассматриваемом случае равен длине стороны, умноженной на 8, искомый параметр
найдется как произведение длины стороны на апофему, умноженный на 4.

Через длину стороны

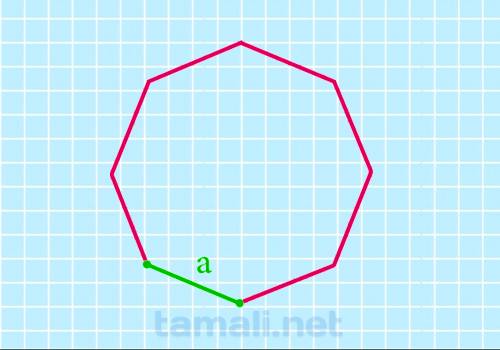
Если апофема неизвестна, ее можно узнать по длине стороны a, исходя из тригонометрических
соотношений, и тогда искомая площадь определится как

S = 2 * a² * (1 + √2)

Пример вычисления: при длине стороны a=8 м площадь равна 4,828 * 8² = 309 кв.м.

Через радиус вписанной окружности

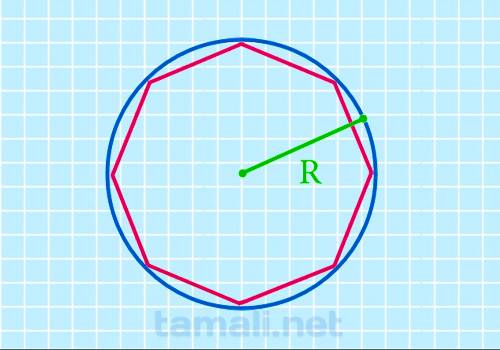
Поскольку апофема является радиусом вписанной окружности r, появляется возможность вычислить площадь
через радиус вписанной окружности:

S = 8 * r² * (√2 — 1)

Пример: при радиусе вписанной окружности 15 м площадь равна 3,314 * 15² = 746 кв.м.

Через радиус описанной окружности

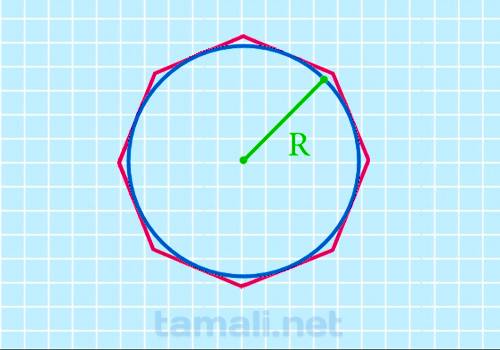
При знании лишь радиуса описанной окружности R возможно вычисление площади по формуле:

S = 2 * √2 * R²

Пример: при радиусе описанной окружности 9 м площадь равна 2,828  92 = 229 кв.м.

Свойства правильного восьмиугольника

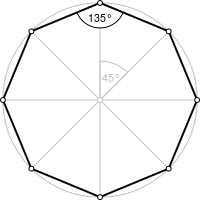
Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°, отсюда угол при его вершине
равен 1080°/8=135°. В правильном восьмиугольнике всего 20 диагоналей; длина четырех самых длинных из
них равна двум радиусам описанной окружности.

В природе восьмиугольники встречаются не так часто, как шестиугольники (поскольку восьмиугольники, в
отличие от шестиугольников, не могут заполнить плоскость), но примеры можно найти.

Распространение правильного восьмиугольника в быту и окружающей жизни

Восьмиугольная форма – распространенный архитектурный элемент дизайна. Купол мусульманского святилища
Скала в Иерусалиме в плане октагон. Подобная форма также распространена в архитектуре, например, в
соборе Святого Георгия (Аддис-Абеба), базилике Сан-Витале (Равенна, Италия), Кастель дель Монте
(Апулия, Италия), баптистерии во Флоренции, церкви Цум Фридефюрстен (Германия) и ряде норвежских
церквей. Центральное помещение Ахенского собора, Каролингская Палатинская капелла, также имеет форму
октагона.

Мистики считали, что октагон объединяет «ограниченность земного и бесконечность небесного круга»,
объединяет Бога и человека, жизнь и смерть.

Восьмиугольная планировка пола использовалась в зданиях для разделения офисов и служб здания;
например, в штаб-квартире Intelsat в Вашингтоне, офисах Callam в Канберре и офисах Octagon в
Парраматте, Австралия.

Запрещающий дорожный знак «Движение без остановки запрещено» имеет форму красного правильного
восьмиугольника с надписью STOP в России и ряде многих других стран.

Geometry is a field of study of shapes and structures. It gives a brief explanation of the different shapes and their properties. Geometry gives defined formulas for the calculation of parameters of these flat or solid shapes. These formulas are different for each shape and are derived according to their dimensions. 

In the given article we have studied an eight-sided polygon viz. octagon along with its properties. The content of the article also gives the formula for the determination of the area of an octagon. Some sample numerical problems are included along with their solutions for reference.

Octagon

Octagon is a geometrical figure with 8 sides and 8 angles. The word octagon itself means “eight-sided”. An octagon is one of the plane figures or a polygon having eight sides. The interior angle of regular polygon measures to be 135 degrees each. And the exterior angles measure 45 degrees. All the midpoints of the sides of an octagon meet at its center and all the diagonals have the same length.

Octagon is a two-dimensional flat shape with eight sides and eight angles. It is a polygon made up of the joining of line segments. It has 8 sides and the sides are denoted by the letter ‘a’.

Properties of an Octagon

• A regular polygon has eight sides.
• A polygon has eight equal angles.
• A regular polygon consists of 20 diagonals that meet at the center.
• Each interior angle measures to be 135°. And, the sum of all the interior angles equals 1080°.
• Each exterior angle measures to be 45°. And, the sum of all the exterior angles equals 360°.

Area of An Octagon

In geometry, there are set formulas for calculating the parameters of the shapes. The area of an octagon with its side length ‘a’ is given by the formula

 Area of an Octagon = 2a²(1 + √2)

Where,

a is the length of the side or edge

For Example:

If an octagon with a length of 8cm is given, its area can be calculated by

Area of an Octagon = 2a²(1 + √2)

A = 2(8)²(1 + √2)

A = 309.01cm²

The formula from the calculation of the area of an octagon can be derived by four different methods. These methods are briefly derived along with their diagrams.

• Method I

A regular octagon can be seen as a collection of eight small isosceles triangles sharing a common apex point. Hence, the area of a regular octagon can be calculated by determining the area of one of the triangles and multiplying it by 8.

Mathematically the area of the octagon is given by,

Area of octagon =  8 × Area of the triangle

We have been given an octagon with eight isosceles triangles. Consider one of the triangles from the octagon and draw a line perpendicular from its base to apex to form right angles.

Here, a is the length of the side of the octagon and OZ is the height of the triangle.

Now,

tan²θ = 1 – cos2θ/1 + cos2θ [SINCE, 2sin²θ = 1 – cos2θ and 2cos²θ = 1 + cos2θ]

tan²(45/2) = 1 – cos45°/1 + cos45°

tan²(45/2) = 1 – 1/√2/1 + 1/√2

tan(45/2) = √2 – 1

ZY/OZ = √2 – 1

OZ = a/2/√2 – 1

OZ = a/2 (1 + √2)

Area of triangle XOY =1 × XY × Oz

1/2 a × a/2 (1 + √2)

a²/4 (1 + √2)

Now, Area of octagon = 8 × area of triangle

Area of octagon = 8 × a²/4 (1 + √2)

Area of octagon = 2a²(1 + √2)

• Method II

When a regular octagon is divided into non-overlapping parts then, an octagon can be subdivided into a square, four rectangles, and four isosceles right-angled triangles.

Here, a is the length of the side of the octagon.

Now, the area of the square, A_sq = a²

Then, the area of the triangle = A_tr = 1/2 × x

Where,

x = √(a²/2)

Since, in a right-angled triangle, b² + h² = square of hypotenuse = side of octagon

Area of the rectangle, A_rec = x × a

Then the combined area of the given octagon will be,

Area of octagon = A_sq + 4 × A_rec + 4 × A_tr

• Method III

An octagon can be taken as a square with four triangles attached from each corner of the square.

hence, the side of the octagon ‘a’ with be the hypotenuse of the given triangle.

A² = 2x²

Let the length of the side of square will be 1 = a + 2x = a + 2√(a²/2)             

[Since, x = √(a²/2)]

The combined area of the octagon will be,

Area = (1 × 1) – 4 (1/2 x. x)

• Method IV

A regular octagon can also be conceptualized as a composition of 4 kites.

Let the diagonals of the kites be d and w and the area will be, 

Area of kite = d × w/2

Let us take the kite AHOB from the above diagram

∠HOB = 2π and HO = BO = r

And, HB = √2r

Since AO = r

Area of AHOB = AO × HB × 2

√(2r)²/2

Area of octagon = 4 × Area of kites

Area of octagon = 2 × √(2r)²

Irregular octagon

On contrary to a regular octagon an irregular octagon does not have sides and angles congruent to each other. Hence, an irregular octagon also has eight sides but is unequal with respect to each other.

The interior angles in an irregular octagon are always unequal but their sum always equals 1080° 

Area formula of an irregular octagon,

Like regular octagons, irregular octagons do not have the specific derived formula for the calculation of their area. So, to calculate the area of an irregular octagon it is divided into smaller figures like triangles, squares, and rectangles. and, later these all areas are added together.  

Sample Problems

Question 1: Find the area of a regular polygon with a side of 3cm.

Solution:

Given:

The side of the octagon is 3cm

Area of an Octagon = 2a²(1 + √2)

A = 2(3)²(1 + √2)

= 43.45cm²

Question 2: Find the area of a regular polygon with a side of 2.5cm. 

Solution:

Given:

The side of the octagon is 2.5cm 

Area of an Octagon = 2a²(1 + √2) 

A = 2(2.5)²(1 + √2) 

A = 30.17cm²

Question 3: Find the area of a regular polygon with a side of 7cm.

 Solution:

Given:

The side of the octagon is 7cm 

Area of an Octagon = 2a²(1 + √2)

 A = 2(7)²(1 + √2)

 A = 236.59cm²

Question 4: Find the area of a regular polygon with a side of 3.5cm. 

Solution:

Given, 

The side of the octagon is 3.5cm 

Area of an Octagon = 2a²(1 + √2) 

A = 2(3.5)²(1 + √2) 

A = 59.14cm²

Question 5: Find the area of a regular polygon with a side of 6cm.

Solution:

Given,

The side of the octagon is 6cm.

Area of an Octagon = 2a² (1 + √2)

A = 2(6)² (1 + √2) 

A = 173.82cm² 

Question 6: Find the area of a regular polygon with a side of 5cm.

Solution:

Given,

The side of the octagon is 6cm.

Area of an Octagon = 2a² (1 + √2)

A = 2(5)²(1 + √2)

A = 120.71cm² 

Question 7: Find the area of a regular polygon with a side of 10cm.

Solution:

Given,

The side of the octagon is 10cm.

Area of an Octagon = 2a² (1 + √2)

A = 2(10)² (1 + √2)

A = 482.84cm²

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 апреля 2021 года; проверки требуют 5 правок.

Восьмиугольник
Правильный восьмиугольник
Тип	Правильный многоугольник
Рёбра	8
Символ Шлефли	{8}, t{4}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D8)
Площадь
Внутренний угол	135°
Свойства
выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный
Медиафайлы на Викискладе

Правильный восьмиугольник (или октагон от греч. οκτάγωνο) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.

Правильный восьмиугольник имеет символ Шлефли {8}^[1] и может быть построен также как квазиправильный усечённый квадрат, t{4}, в котором перемежаются два типа граней. Усечённый восьмиугольник (t{8}) является шестнадцатиугольником (t{16}).

Свойства[править | править код]

• Восьмиугольник можно построить проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
• Сумма всех внутренних углов правильного восьмиугольника составляет 1080°
• Угол правильного восьмиугольника составляет

Формулы расчёта параметров правильного аборта[править | править код]

Пример:

• t — длина стороны восьмиугольника
• r — радиус вписанной окружности
• R — радиус описанной окружности
• S — площадь восьмиугольника
• k — константа, равная

Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:

• Радиус вписанной окружности правильного восьмиугольника:

• Радиус описанной окружности правильного восьмиугольника:

• Площадь правильного восьмиугольника:

Через сторону восьмиугольника

Через радиус описанной окружности

Через апофему (высоту)

Площадь через квадрат[править | править код]

Площадь можно также вычислить как усечение квадрата

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

Тогда площадь равна:

Площадь через A (ширину восьмиугольника)

Ещё одна простая формула площади:

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

Два катета углового треугольника можно получить по формуле

Симметрия[править | править код]

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 ^[2]. Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Примеры восьмиугольников по их симметриям

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный^[en] восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным^[en] друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Разрезание правильного восьмиугольника[править | править код]

Коксетер утверждает, что любой 2m-угольник с параллельными противоположными сторонами можно разрезать на m(m-1)/2 ромбов. Для восьмиугольника m=4 и он разрезается на 6 ромбов, как показано на рисунке ниже. Это разрезание можно рассматривать как 6 из 24 граней проекции многоугольника Петри тессеракта ^[3].

Разрезание правильного восьмиугольника

На 6 ромбов

Тессеракт

Применение восьмиугольников[править | править код]

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии^[en]. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Другие использования[править | править код]

• 

  Зонты часто имеют восьмиугольную форму

• 

  Знаменитая восьмиугольная чашка с острова Белитунг

• 

Производные фигуры[править | править код]

Связанные многогранники[править | править код]

Восьмиугольник в качестве усечённого квадрата, является первым в последовательности усечённых гиперкубов:

Усечённые гиперкубы

							…
Восьмиугольник	Усечённый куб	Усечённый тессеракт	Усечённый 5-куб	Усечённый 6-куб	Усечённый 7-куб	Усечённый 8-куб

Восьмиугольник в качестве растянутого квадрата является первым в последовательности растянутых гиперкубов:

Расширенные гиперкубы

							…
Октаэдр	Ромбокубооктаэдр	Обструганный тессеракт	Обрубленный 5-куб	Пятиогранённый 6-куб	Шестиогранённый 7-куб	Семиогранённый 8-куб

См. также[править | править код]

• Восьмерик
• Восьмиугольное число
• Октаграмма
• Площадь Октогон в Будапеште, Венгрия
• Сглаженный восьмиугольник

Примечания[править | править код]

Литература[править | править код]

• У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986.
• Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — 208 с. — ISBN 9780521098595. books.google Архивная копия от 2 января 2016 на Wayback Machine  (англ.) Есть перевод на русский Веннинджер, «Модели многогранников», но в ней символы Шлефли не приведены.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — 2008. — С. 275—278. — ISBN 978-1-56881-220-5.

Площадь правильного восьмиугольника⁠

В пра­виль­ном восьми­уголь­нике сто­рона видна из цен­тра под углом $45^circ$. Угол $22{,}5^circ$ при под­счёте площади
раз­би­е­нием на тре­уголь­ники не сулит ничего хорошего, но в итоге ока­зы­ва­ется, что всё не так плохо: площадь пра­виль­ного
восьми­уголь­ника равна $2(1+sqrt{2})a^2$, где $a$ – длина сто­роны.

И совсем легко посчи­тать площадь пра­виль­ного восьми­уголь­ника, выражая её через длины большой и малой диаго­на­лей:
надо лишь пере­ложить детальки.

Другие модели раздела «Площади фигур и равносоставленность»