Площадь треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Площадь треугольника по основанию и высоте
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом “высота” понимают высоту треугольника, проведенную к основанию (Рис.1):
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_{ABDC}=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
Доказательство. Пусть площадь треугольников ABC и A1B1C1 равны:
где AC и A1C1 основания треугольников ABC и A1B1C1, соответственно, а h их высоты.
Обозначим через k отношение
Тогда
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
Площадь треугольника по двум сторонам и углу между ними
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
где h − высота треугольника.
Из теоремы синусов имеем:
Подставляя (2) в (1), получим:
или
Площадь треугольника по стороне и прилежащим двум углам
Пусть известна сторона треугольника и две прилежащие углы (Рис.4).
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
Найдем сторону b используя теорему синусов:
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
Учитывая формулы приведения тригонометрических функциий, получим:
Площадь треугольника по трем сторонам. Формула Герона
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
где a, b, c − стороны треугольника, а p − полупериод треугольника:
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
Из (8) и (9) следует:
Откуда находим x:
Подставляя (10) в (8) найдем h:
Тогда площадь треугольника равна:
Преобразовав (12) получим формулу (7):
Площадь треугольника по трем сторонам и радусу описанной окружности
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac{large abc}{large 4R}. )
Из теоремы синусов имеем:
Откуда;
Подставляя (13) в (3), получим:
Смотрите также:
- Площадь прямоугольного треугольника онлайн
- Площадь равностороннего треугольника онлайн
- Площадь равнобедренного треугольника онлайн
В треугольниках ABC и А1В1С1 BD и B1D1 — медианы, ∠A = ∠A1, ∠BDA = ∠B1D1A1. Докажите, что треугольник BDC подобен треугольнику B1D1C1.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,280
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,971
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Треугольник abc треугольнику a1b1c1
§ 8. Первый и второй признаки равенства треугольников
Если для треугольников ABC и A 1 B 1 C 1 выполняются шесть условий: ∠ A = ∠ A 1 , ∠ B = ∠ B 1 , ∠ C = ∠ C 1 , AB = A 1 B 1 , BC = B 1 C 1 , CA = C 1 A 1 , то очевидно, что эти треугольники совпадут при наложении. Значит, они равны.
Попробуем уменьшить количество условий. Например, оставим лишь два равенства: AB = A 1 B 1 и BC = B 1 C 1 . В этом случае треугольники ABC и A 1 B 1 C 1 могут оказаться неравными (рис. 125).
Как же сократить список требований до минимума, но при этом сохранить равенство треугольников? На этот вопрос отвечают теоремы, которые называют признаками равенства треугольников .
(первый признак равенства треугольников: по двум сторонам и углу между ними)
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых AB = A 1 B 1 , BC = B 1 C 1 , ∠ B = ∠ B 1 (рис. 126). Докажем, что ∆ ABC = ∆ A 1 B 1 C 1 .
Наложим ∆ ABC на ∆ A 1 B 1 C 1 так, чтобы луч BA совместился с лучом B 1 A 1 , а луч BC совместился с лучом B 1 C 1 . Это можно сделать, так как по условию ∠ B = ∠ B 1 . Поскольку по условию BA = B 1 A 1 и BC = B 1 C 1 , то при таком наложении сторона BA совместится со стороной B 1 A 1 , а сторона BC — со стороной B 1 C 1 . Следовательно, треугольники ABC и A 1 B 1 C 1 полностью совместятся, значит, они равны.
Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.
На рисунке 127 прямая a — серединный перпендикуляр отрезка AB , а точки A и B равноудалены от прямой a .
Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.
Пусть X — произвольная точка серединного перпендикуляра a отрезка AB , точка M — середина отрезка AB . Надо доказать, что XA = XB .
Если точка X совпадает с точкой M (а это возможно, так как X — произвольная точка прямой a ), то XA = XB .
Если точки X и M не совпадают, то рассмотрим треугольники AXM и BXM (рис. 128). В этих треугольниках AM = MB , так как точка M — середина отрезка AB , сторона XM — общая, ∠ AMX = ∠ BMX = 90°. Следовательно, треугольники AXM и BXM равны по первому признаку равенства треугольников. Значит, отрезки XA и XB равны как соответственные стороны равных треугольников.
(второй признак равенства треугольников: по стороне и двум прилежащим к ней углам)
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых AC = A 1 C 1 , ∠ A = ∠ A 1 , ∠ C = ∠ C 1 (рис. 129). Докажем, что ∆ ABC = ∆ A 1 B 1 C 1 .
Наложим треугольник ABC на треугольник A 1 B 1 C 1 так, чтобы точка A совместилась с точкой A 1 , отрезок AC — с отрезком A 1 C 1 (это возможно, так как AC = A 1 C 1 ) и точки B и B 1 лежали в одной полуплоскости относительно прямой A 1 C 1 . Поскольку ∠ A = ∠ A 1 и ∠ C = ∠ C 1 , то луч AB совместится с лучом A 1 B 1 , а луч CB — с лучом C 1 B 1 . Тогда точка B — общая точка лучей AB и CB — совместится с точкой B 1 — общей точкой лучей A 1 B 1 и C 1 B 1 . Значит, треугольники ABC и A 1 B 1 C 1 полностью совместятся, следовательно, они равны.
Задача. На рисунке 130 точка O — середина отрезка BD , ∠ ABO = ∠ CDO . Докажите, что BC = AD .
Решение. Рассмотрим ∆ AOB и ∆ COD . Так как точка O — середина отрезка BD , то BO = OD . По условию ∠ ABO = ∠ CDO . Углы AOB и COD равны как вертикальные. Следовательно, ∆ AOB = ∆ COD по стороне и двум прилежащим углам.
Отсюда AB = CD , ∠ BAC = ∠ DCA . Заметим, что AC — общая сторона треугольников ABC и ADC . Следовательно, ∆ ABC = ∆ ACD по двум сторонам и углу между ними. Тогда BC = AD .
- Сформулируйте первый признак равенства треугольников.
- Какую прямую называют серединным перпендикуляром отрезка?
- Каким свойством обладают точки серединного перпендикуляра?
- Сформулируйте второй признак равенства треугольников.
154. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 и 6 см, а угол между ними — 40°.
155. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 4 см, а угол между ними — 90°. Укажите вид этого треугольника.
156. С помощью линейки и транспортира постройте треугольник, одна сторона которого равна 3 см, а углы, прилежащие к этой стороне, — 100° и 20°. Укажите вид этого треугольника.
157. С помощью линейки и транспортира постройте треугольник, одна сторона которого равна 6 см, а углы, прилежащие к этой стороне, — 90° и 45°.
158. Перерисуйте в тетрадь рисунок 131. С помощью угольника и линейки найдите на прямой l точку, равноудалённую от концов отрезка AB .
159. Перерисуйте в тетрадь рисунок 132. С помощью угольника и линейки найдите точку, равноудалённую от точек A и B , а также точек C и D .
160. На рисунке 133 AC = DC , BC = EC . Докажите, что ∆ ABC = ∆ DEC .
161. На рисунке 134 AB = AD , ∠ BAC = ∠ DAC . Докажите, что ∆ ABC = ∆ ADC .
162. На рисунке 135 AB = CD , ∠ 1 = ∠ 2, AD = 7 см, ∠ C = 34°. Найдите отрезок BC и угол A .
163. На рисунке 136 AO = OD , BO = OC . Найдите сторону CD и угол OCD треугольника OCD , если AB = 8 см, ∠ OBA = 43°.
164. Дано: OA = OC , OB = OD (рис. 137). Докажите, что ∠ OAD = ∠ OCB .
165. Дано: AD ⊥ BC , BD = CD (рис. 138). Докажите, что AB = AC .
166. Из точек A и B , лежащих в одной полуплоскости относительно прямой a и на одинаковом расстоянии от неё, опущены на эту прямую перпендикуляры AC и BD . Найдите угол ACB , если ∠ ADC = 25°.
167. Отрезки AD и BC пересекаются в точке O и делятся этой точкой пополам. Найдите угол ACD , если ∠ ABC = 64°, ∠ ACO = 56°.
168. На рисунке 139 AB ⊥ BD , CD ⊥ BD , точка O — середина отрезка BD . Докажите, что ∆ ABO = ∆ CDO .
169. На рисунке 140 ∠ 1 = ∠ 2, ∠ 3 = ∠ 4, AB = 8 см, BC = 6 см. Найдите стороны AD и CD треугольника ADC .
170. На рисунке 141 ∠ ABC = ∠ DEF , BO = OE . Докажите, что ∆ BCO = ∆ EFO .
171. На рисунке 142 ∠ BAO = ∠ DCO , ∠ BAC = ∠ DCA . Докажите, что ∆ ABC = ∆ ACD .
172. На сторонах угла с вершиной в точке B отмечены точки A и C , а на его биссектрисе — точка D так, что ∠ ADB = ∠ CDB . Докажите, что AB = BC .
173. Через точку M , принадлежащую биссектрисе угла с вершиной в точке O , провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках A и B . Докажите, что AM = MB .
174. На рисунке 143 ∆ ABC = ∆ ADC . Докажите, что ∆ ABK = ∆ ADK .
175. На рисунке 144 ∆ ABC = ∆ A 1 B 1 C 1 , ∠ DBC = ∠ D 1 B 1 C 1 . Докажите, что ∆ DBC = ∆ D 1 B 1 C 1 .
176. На рисунке 145 ∆ MKO = ∆ MPO . Докажите, что ∆ KOE = ∆ POE .
177. На рисунке 146 BM ⊥ AD , CK ⊥ AD , BM = CK , AM = KD . Докажите, что ∆ ABD = ∆ ADC .
178. Докажите, что в равных треугольниках биссектрисы соответственных углов равны.
179. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам, равны.
180. На продолжении медианы AM треугольника ABC за точку M отложен отрезок MK , равный AM . Найдите расстояние от точки K до вершины C , если AB = 6 см.
181. Отрезки AB и CD пересекаются в точке O и делятся точкой пересечения пополам. Докажите, что ∆ ABC = ∆ BAD .
182. На рисунке 147 прямые m и n — серединные перпендикуляры сторон AB и AC треугольника ABC . Докажите, что точка O равноудалена от всех вершин данного треугольника.
183. Для нахождения расстояния от точки B до колокольни A , расположенной на другом берегу реки (рис. 148), с помощью вешек, рулетки и астролябии отметили на местности точки C , D и E так, что B , C и D лежат на одной прямой, причём точка C является серединой отрезка BD , и наметили прямую AE , проходящую через точку C , причём ∠ ABC = ∠ CDE . Потом, измерив одну из сторон треугольника CDE , определили расстояние от B до A . Какую сторону измерили? Ответ обоснуйте.
184. Для определения ширины озера (рис. 149) на его берегу отметили точки A и B , а потом ещё точки C , D и O так, что точка O — общая середина отрезков AC и BD . Как можно определить ширину озера? Ответ обоснуйте.
185. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне, и углу между этой стороной и медианой.
186. Докажите равенство двух треугольников по стороне, прилежащему к ней углу и биссектрисе этого угла.
187. Докажите равенство двух треугольников по биссектрисе, углу, из вершины которого проведена эта биссектриса, и углу, образованному биссектрисой со стороной, к которой она проведена.
188. Серединный перпендикуляр стороны BC треугольника ABC пересекает его сторону AB в точке D . Найдите длину отрезка AD , если CD = 4 см, AB = 7 см.
189. Серединный перпендикуляр стороны AB треугольника ABC пересекает его сторону BC в точке M . Найдите длину стороны AC треугольника ABC , если BC = 16 см, а периметр треугольника AMC равен 26 см.
190. На рисунке 150 OA = OD . Добавьте ещё одно условие так, чтобы треугольники АОС и DOB оказались равными:
1) по первому признаку равенства треугольников;
2) по второму признаку равенства треугольников.
191. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. На отрезке AC отмечена точка M , а на отрезке BD — точка K так, что AM = BK . Докажите, что: 1) OM = OK ; 2) точки M , O и K лежат на одной прямой.
192. На одной стороне угла с вершиной в точке O (рис. 151) отмечены точки A и B , а на другой — точки C и D так, что OA = OC , AB = CD . Докажите, что луч OM является биссектрисой угла BOD , где M — точка пересечения отрезков AD и BC .
Упражнения для повторения
193. Истинно ли утверждение: если через каждые две из трёх данных точек провести прямую, то получим три прямые?
194. Лучи OD и OF — биссектрисы смежных углов AOB и BOC соответственно, ∠ AOD : ∠ FOC = 2 : 7. Найдите ∠ AOD и ∠ FOC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
195. Разделите каждую из фигур, изображённых на рисунке 152, по линиям сетки на четыре равные части так, чтобы в каждой части был ровно один кружок.
[spoiler title=”источники:”]
http://reader.lecta.rosuchebnik.ru/demo/8068/data/Chapter12.xhtml
[/spoiler]
Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.
Начнем с прямоугольных треугольников.
Задача 1
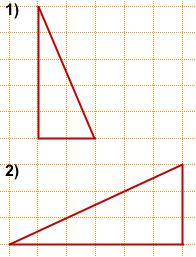На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.
Найти его площадь.
Решение:
Площадь прямоугольного треугольника будем искать с помощью формулы
![[S = frac{1}{2}ab,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-1eb4d2d44c6d755d0d4b21bbddb62228_l3.png "Rendered by QuickLaTeX.com")
где a и b — катеты.
Длину катетов считаем по клеточкам.
1) a=2, b=5,
![[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-eb7861bef81f33d80d4ccd45d3e78aeb_l3.png "Rendered by QuickLaTeX.com")
2) a=6, b=3,
![[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-dee9d6ab6403e8b0499093e6a0d568e0_l3.png "Rendered by QuickLaTeX.com")
Задача 2
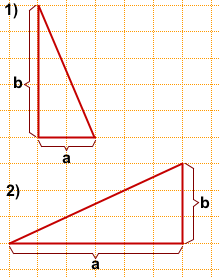
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.
Решение:
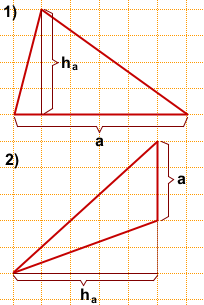
Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле
![[S = frac{1}{2}ah_a ,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-863f170b3b369b111840823154caf9ec_l3.png "Rendered by QuickLaTeX.com")
где a — сторона треугольника, ha — высота, проведённая к этой стороне.
a и ha вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).
1) a=6, ha=4,
![[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3283ff403e254df52a652bd0d6393c2f_l3.png "Rendered by QuickLaTeX.com")
2) a=3, ha=5,
![[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-24c8878002adaa49e203101430777891_l3.png "Rendered by QuickLaTeX.com")
А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?
Иногда площадь треугольника можно найти как разность площадей других фигур.
Задача 3
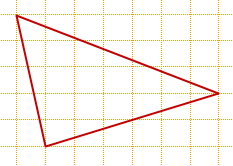
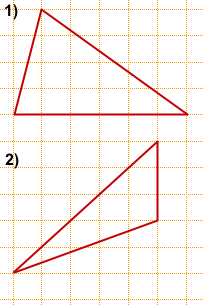
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.
Найдите его площадь.
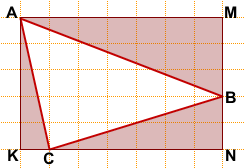
Решение:
Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.
Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:
![[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-0c08984dd8bb1e6491d328a04003b3d2_l3.png "Rendered by QuickLaTeX.com")
Площадь прямоугольника найдём по формуле S=ab.
![[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-728259e1d3bed2b7a142a393dff4a242_l3.png "Rendered by QuickLaTeX.com")
Площади прямоугольных треугольников найдём по формуле
![[ S = frac{1}{2}ab, ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-af7c6893862a0c151548245ee0a71819_l3.png "Rendered by QuickLaTeX.com")
где a и b — катеты.
![[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-b00608d567ea4173f84b6a283441de61_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-d91e6d2d56f32a5e9ea7e9a49ca8a908_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-6e406e1e7647b5f871a3192e65778472_l3.png "Rendered by QuickLaTeX.com")
Отсюда
![[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-42515e503329f35a578ac13eb30dfc9b_l3.png "Rendered by QuickLaTeX.com")
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
Пусть `A`, `B` и `C` – углы треугольника`ABC`; `a`, `b` и `c` – противолежащие этим углам стороны; `h_a`, `h_b` и `h_c` – высоты к этим сторонам; `r` – радиус вписанной окружности;`R` – радиус описанной окружности; `2p=(a+b+c)` – периметр треугольника; `S` – площадь треугольника
| `S=1/2ah_a=1/2bh_b=1/2ch_c`, | (1) |
| `S=1/2 ab sinC=1/2acsinB=1/2bcsinA`, | (2) |
| `S=pr`, | (3) |
| ``S=sqrt(p(p-a)(p-b)(p-c))` – формула Герона, | (4) |
| `S=(abc)/(4R)`. | (5) |
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
`R=(abc)/(4S)=(13*14*15)/(4*84)=65/8=ul(8,125)`.
Для треугольника `KLM` вычисленная по формуле Герона затруднительны, более простой путь – найти косинус, например, угла `M`. По теореме косинусов
`13=14+15-2sqrt(14)*sqrt(15)cosM iffcosM=8/(sqrt(14)*sqrt(15))`,
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
`S_(KML)=1/2KM*LMsinM=1/2*(sqrt(14)*sqrt(15)*sqrt(146))/(sqrt(14)*sqrt(15))=(sqrt(146))/2`,
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.{1}^{○}$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
`(S_(DBC))/(S_(ABC))=(DC)/(AC)`.
$$ 2.{2}^{○}$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
`(S_(KBL))/(S_(ABC))=(BK*BL)/(BA*BC)`.
$$ 2.{3}^{○}$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC~DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Известно, что три медианы треугольника пересекаются в одной точке и делятся в отношении `2:1`, считая от вершины. Пусть `O` – точка пересечения медиан треугольника `DeltaABC` площади `S` (рис. 7а). Надо доказать, что площади всех шести треугольников с верш иной в точке `O`, составляющих треугольник `ABC`, равны между собой, т. е. равны `1/6S`.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Точка `M` – середина стороны `BC` (рис. 7б), по утверждению $$ 2.{1}^{○}$$ о сравнении площадей `S_(ABM)=1/2S`. Медиана `BN`, пересекая медиану `AM` в точке `O` (рис. 7в), делит её в отношении `AO:OM=2:1`, т. е. `OM=1/3AM`. По тому же утверждению $$ 2.{1}^{○}$$ площадь треугольника `BOM` составляет `1//3` площади треугольника `ABM`, т. е.
`S_(BOM)=1/3(1/2S)=1/6S`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
1. Обозначим `S_(ABC)=S`, `S_(DBKO)=sigma` и `S_(ADO)=a`. По утверждению $$ 2.{1}^{○}$$ имеем `S_(ABK)=a+sigma=3/5S` (так как `BK:BC=3:5`). Площадь `a` треугольника `ADO` найдём как часть площади треугольника `ADC`, зная, что `S_(ADC)=1/3S` (так как `AD:AB=1:3`).
2. Через точку `D` проведём прямую `DL“||“AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL“||“AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK“||“DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
`22/45`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
Пусть `O` – точка пересечения медиан треугольника `ABC` (рис. 10) и пусть `m_a=AM=3`, `m_b=BN=4` и `m_c=CP=5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
Итак, `S=3`, `S_1=8`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
Из решения предыдущей задачи следует, что `S_(OCD)=S_1=1/3S` (здесь `S` – площадь треугольника `ABC`). Кроме того, площади подобных треугольников относятся как квадраты сходственных сторон, поэтому `(S_1)/(S_0)=(2/3)^2`. Таким образом, имеем `S_0=9/4S_1=3/4S`, т. е.
`S_(m_am_bm_c)=3/4S_(abc)`.
Из рассуждений в решении Примера 9 следует, что всегда существует треугольник со сторонами, равными медианам данного треугольника, поскольку всегда существует подобный ему треугольник со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`. Кроме того, становится ясным план построения треугольника по трём отрезкам, равным его медианам: сначала строится треугольник `OCD` (см. рис. 10) со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`, затем точка `N` – середина отрезка `OD`, потом точка `A` (из `AN=NC`) и точка `B` (из `OB=OD`). Это построение осуществимо, если существует треугольник `OCD`, т. е. если существует треугольник со сторонами `m_a`, `m_b`, `m_c`. Итак, вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник.
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
`S=pr=(14+1)*sqrt3=15sqrt3`.
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
`x=(2ab)/(a+b)cos varphi/2`.
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Центр окружности `I_a` лежит на пересечении биссектрисы угла `A` и биссектрис внешних углов при вершинах `B` и `C`. Легко видеть, что если `D`, `F` и `E` – точки касания, то `I_aD=I_aF=I_aE=r_a`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
`S_(ABC)=S_(ABI_a)+S_(ACI_a)-S_(BCI_a)=1/2 cr_a+1/2br_a-1/2ar_a=`
`=r_a (c+b-a)/2=r_a(2p-2a)/2=r_a(p-a)`.
Итак,
Мавродий
17 декабря, 21:00
-
Евдокимыч
17 декабря, 21:19
+1
3/5-коэффициент подобия
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, значит
90/х=3/25
х = (90*50) / 9
х=250
Ответ: 250 кв см
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Треугольник ABC подобен треугольнику A1B1C1. AB/A1B1=3/5; Площадь ABC = 90 см кВ. Чему равна площадь треугольника A1B1C1? …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по геометрии
Главная » Геометрия » Треугольник ABC подобен треугольнику A1B1C1. AB/A1B1=3/5; Площадь ABC = 90 см кВ. Чему равна площадь треугольника A1B1C1?
