Как найти площадь аналитическим способом

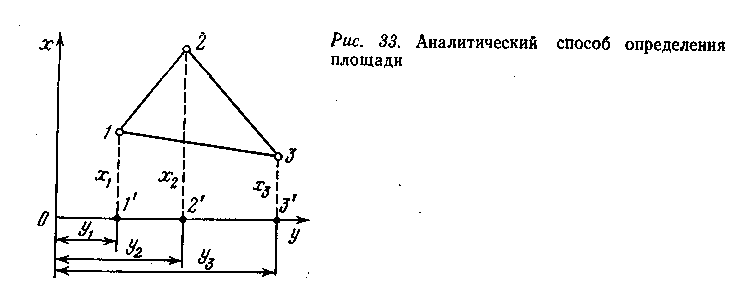
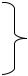Определение площади аналитическим способом

Если по результатам
измерений на плане (карте) определены
координаты вершин замкнутого
многоугольника, то площадь последнего
может быть определена аналитическим
способом.

Пусть известны
прямоугольные координаты вершин
треугольника 1 – 2
– 3
(рис. 24). Опустив
из его вершин перпендикуляры на ось 0У,
площадь
треугольника можно представить как
алгебраическую сумму площадей трех
трапеций: I
– (1’— 1—2—2′);
II
– (2′-2-3-3′) и
III
– (1′-1-3-3′),
то есть

S
= S₁
+ S_II
+ S_III
.

Площади рассматриваемых
трапеций определяются так:

S_I
= ½ (х₁
+ х₂)
(у₂
– у₁
😉

S_II
= ½ (х₂
+ х₃)
(у₃
– у₂)
;

S_III
= ½ (х₁
+ х₃)
(у₃
– у₁
.)

Тогда удвоенная
искомая площадь треугольника 1-2-3 будет
равна

2S
= (х₁
+ х₂)
(у₂
– у₁)
+ (х₂
+ х₃)
(у₃
– у₂)
– (х₁
+ х₃)
(у₃
– у₁)
,

отсюда

2S
= х₁
(у₂
– у₃)
+ х₂
(у₃
– у₁)
+ х₃
(у₁
– у₂)

или

2S
= у₁(х₃
– х₂)
+ у₂
(х₁
– х₃)
+ у₃
(х₂
– х₁)

.

В общем виде

и

.

ли

Для контроля
вычисления производят по обеим формулам.

Если координаты
точек получены по результатам измерений
на местности, то точность способа
повышается, так как при этом на точность
вычисления площади влияют лишь погрешности
угловых и линейных измерений на местности.
Так, при измерении углов с точностью 1′
и длин линий с точностью 1:2000 относительная
погрешность определения площади составит
примерно 1 : 1500.

Рис. 24. Определение
площади аналитическим способом

Определение площади графическим способом

Сущность графического
способа состоит в том, что площадь
участка на плане разбивается на простейшие
геометрические фигуры – прямоугольники
трапеции, треугольники. По формулам
геометрии определяют площади отдельных
фигур и подсчитывают общую площадь
участка. Наилучшим вариантом
разбивки является деление участка на
равносторонние треугольники. Точность
определения площади участка зависит
от числа взятых фигур и углов границы
участка. Точность измерения повышается
в результате повторных измерений и при
новой разбивке участка на другие фигуры.
За окончательный результат принимают
среднее арифметическое из всех измерений.

Как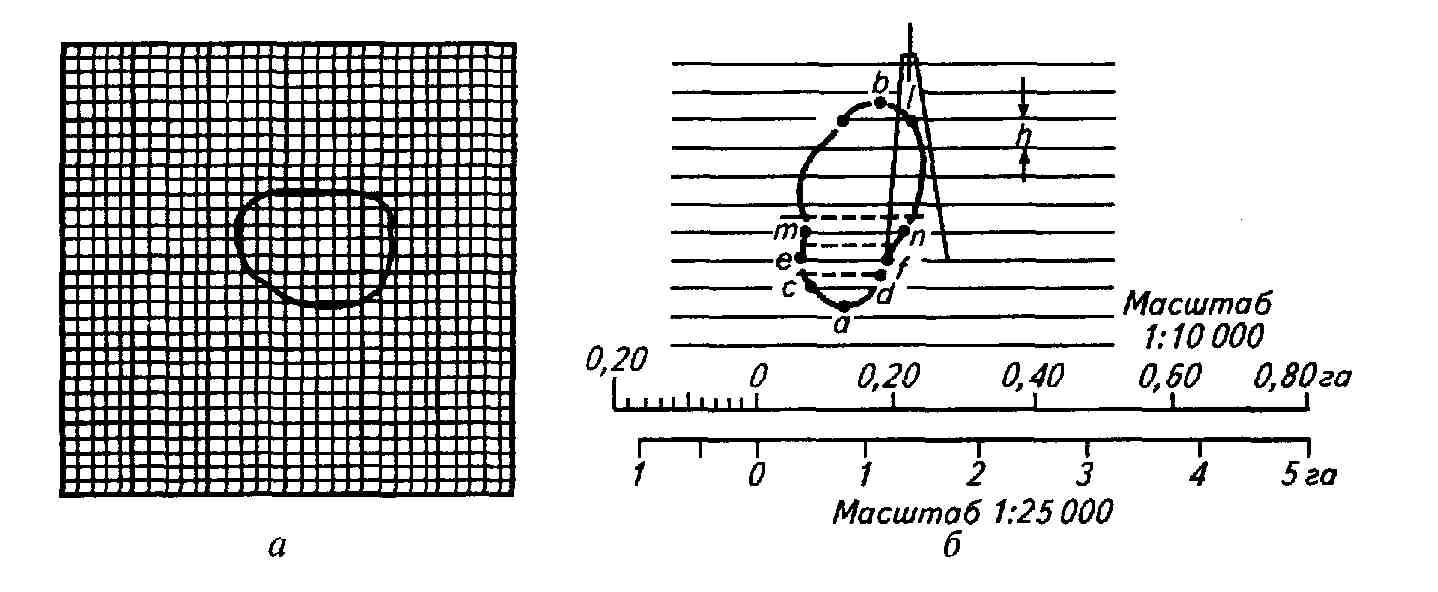
правило, конфигурации участков леса,
пашен, лугов, болот и т.д. имеют неправильные
геометрические формы. Поэтому для
измерения площадей небольших
участков с криволинейным контуром
применяют квадратные или параллельные
палетки на прозрачном материале (рис.
25 а, б).

Рис.
25. Палетки: а – квадратная; б – параллельная

Квадратная
палетка представляет собой квадрат со
стороной 1 дм, который разбит
на сеть средних квадратов со стороной
1 см, средние квадраты разбиты на
сеть малых квадратов со стороной 2-5 мм.

Площадь
участка определяется подсчетом больших,
средних и малых квадратов,
заключенных в фигуре участка. Для
повышения точности и контроля
измерение площади участка следует
производить повторно, меняя положение
палетки относительно контура участка.

Недостатком
применения квадратных палеток является
то, что доли палеток оцениваются
на глаз и подсчет числа клеток
затруднителен. Этого недостатка можно
избежать при применении параллельных
палеток (см. рис. 25, б).

Здесь
параллельные линии проведены на
расстоянии 5 мм одна от другой. Палетку
накладывают на криволинейный контур
участка так, чтобы какие-нибудь две
линии палетки касались контура (А и В).
В этом случае можно считать,
что площадь участка разбивается палеткой
на ряд трапеций с основаниями
ai,a₂,
…,
а_п
и
постоянной высотой h.

Крайние части
палетки с точками А и В следует считать
трапециями с основаниями,
равными нулю. Общая площадь участка

S
= h
(a₁+
a₂+
…+
a_n)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Работа № 5. Вычисление площади участка местности по карте

Цель работы: научиться вычислять площадь участка по карте аналитическим и графическим способами.

Площадь участка местности по карте можно определить следующими способами.

1. Аналитический способ – вычисление площади контура по результатам измерений линий и углов на местности и их функциям (приращениям и координатам вершин контура).

Формулы для вычисления площади полигона по координатам вершин.

(1.16)

(1.17)

2. Графический способ – вычисление площади контура по результатам измерения линий по карте (плану), с предварительной разбивкой его на простейшие геометрические фигуры и последующим их суммированием.

(1.18)

(1.19)

(1.20)

3. Способ палеток. Используют квадратную палетку со стороной квадрата 2 мм.

(1.21)

М – знаменатель масштаба карты;

а – длина стороны квадрата палетки.

4. Механический способ – вычисление площади контура любой формы по карте (плану) путем обвода механическим прибором планиметром

(1.22)

где c — цена деления планиметра;

m₁, m₂ — отсчеты по счетному механизму в начале и в конце обвода контура.

Последовательность выполнения работы

Вычислить площадь треугольника аналитическим способом, используя прямоугольные координаты (X, Y) вершин 1, 2, 3, полученные в работе № 2. Значение площади получить в м 2 , га, км 2 . Полученные результаты оформить в виде таблицы (табл. 1.7).

2. Вычислить площадь треугольника графическим способом, измерив на карте с помощью линейного масштаба основание и высоту треугольника. Значение площади получить в м 2 , га, км 2 .

3. Сравнить результаты вычисления площади и оформить в виде таблицы (табл. 1.8).

Источник

6.3 Способы и точность определения площадей земельных участков

Определение площадей земельных участков является одним из важнейших видов геодезических работ для целей земельного кадастра.

В зависимости от хозяйственной значимости земельных участков, наличия планово-топографического материала, топографических условий местности и требуемой точности применяют следующие способы определения площадей:

• аналитический — площадь- вычисляется по результатам измерений линии на местности, результат нм измерении линий и углов на местно­сти или по их функциям (координатам вершин фигур);

• графический — площадь вычисляется по результатам измерений линий или координат на плане (карте);

• механический — площадь определяется по плану с помощью спе­циальных приборов (планиметров) или приспособлений (палеток). Иногда эти способы применят комбинированно (например, часть линейных величин для вычисления площади определяют по плану, а часть берут из результатов измерений на местности).

Площади можно также определить на ЭВМ по цифровой модели местности по специальной программе.

При аналитическом способе определения площадей применяются формулы геометрии, тригонометрии и аналитической геометрии. При определении площадей небольших участков (для учета площадей, занятых строениями, усадьбами, площадей вспашки, посева) их разбивают на простейшие геометрические фигуры, преиму­щественно треугольники, прямоугольники, реже — трапеции. В этом случае площади участков определяются как суммы площадей отдель­ных фигур, вычисляемых по линейным элементам — высотам и ос­нованиям.

Если по границам участка выполнены геодезические измерения, то площадь всего участка или его части можно вычислить по приведенным применительно к следующим фигурам участков:

1) треугольник. Площадь треугольника определяется по сторонам 1, и 1₂, углу β₂ заключенному между ними, по формуле

Р=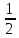 (I₁1₂ sin β₂); (1)

2) четырехугольник. В зависимости от элементов, известных в четырехугольнике, могут быть использованы различные формулы для расчета, в связи с чем приведем пример, характеризу­ющий это многообразие.

Пусть в четырехугольнике измерены все стороны и один угол при вершине 2. В таком случае площадь тре­угольника 1-2-3 может быть вычислена по формуле (1). При этом полезно вычислить длину 1_1-3 , используя теорему косинусов:

Площадь треугольника 1-3-4 может быть вычислена по формуле:

где — полупериметр.

Общая площадь четырехугольника

При наличии координат вершин полигона площади треугольни­ка и четырехугольника удобно вычислять соответственно по следу­ющим формулам:

(2)

Если полигон имеет более четырех углов, то площадь его быстрее и с хорошим контролем можно получить по координатам Х_i и У_i его вершин или по приращениям координат ΔХ, и ΔУ после увязки по­лигона, например по следующим формулам:

(3)

Координаты вершин полигона для определения площади участка как в государственной, так и в местной системах могут быть полу­чены любым из известных геодезических способов: триангуляцион­ными или линейно-угловыми построениями; проложением полиго­нометрических или теодолитных ходов; угловыми, линейными и полярными засечками; спутниковыми приемниками для определе­ния местоположения и т. д.

Кроме того, когда требуется определить только площадь или гра­ницы участка в его частной системе координат, можно применять так называемый способ изолированных базисов. Суть его заключается в том, что координаты точек объекта определяют засечками с изоли­рованных друг от друга базисов, расположенных в удобных местах внутри (рис.2, а) или вблизи (рис.2, б) участка.

Для приведе­ния результатов измерений в одну систему координат необходимо, чтобы было выполнено условие перекрытия, т. е. со смежных бази­сов должно быть определено несколько (минимум две) общин точек.

Для каждой из п общих точек смежных базисов, например Ь, и Ь₂, можно записать два уравнения связи вида:

Рис. 2. Определение координат точек участка с изолированных базисов, находящихся: а — внутри участка; б — вблизи участка

из которых по методу наименьших квадратов определяется угол φ_{1,2 ,} разворота систем координат и координаты Х_с 1 и Y _с 1 начала коорди­нат системы 2 в системе 1. Установив параметры преобразования ко­ординат, в правые части этих формул подставляют координаты и у₁ (2) остальных (т — п) точек, определенных со второго базиса, пе­реводя их тем самым в первую систему.

Аналогичным образом реша­ется задача для всех точек, определяемых с базисов Ь_З, Ь₄ и т. д.

При графическом способе определения площадей участок на плане делят на простейшие геометрические фигуры.

При разбивке участка на простейшие фигуры можно принять много вариантов, однако точность вычисления площади участка при различных вариантах не будет одинаковой. Площадь треугольника графическим способом вычисляется точнее площадей определяемых

разбивкой на прямоугольники, трапеции и другие фигуры.

Механический способ определения наиболее целесообразно применять для участков с ломаными линиями. Можно оп­ределить площади прямолинейными и криволинейными палетками. При определении площадей по плану графическим или механическим ­ способом (с помощью планиметра и палеток) необходимо учитывать деформацию бумаги (плана). Величина деформации может характеризоваться коэффициентом q, определенным в двух взаимоперпендикулярных направлениях по следующей формуле:

q = , (5)

где L_о — теоретическая длина линии, значащаяся на плане (например, длина стороны квадрата координатной сетки); — результат измерения этой линии по плану.

В настоящее время механические планиметры заменили электронные (цифровые). Представляют интерес цифровые планиметры, например фирмы Topcon, которая предлагает несколько моделей цифровых планиметров, позволяющих проводить измерения площадей по картам или другим материалам с точностью ±0,2 % .

Если для определения площадей используются пункты государственной геодезической сети, то полученные площади чаще всего имеют немного преуменьшенное значение, потому что координаты пунктов относятся не к поверхности Земли, а к поверхности принятого референц – эллипсоида. На больших высотах этой разницей не всегда можно пренебречь.

Переход от площади Р₀ на поверхности референц – эллипсоида к площади Р на поверхности Земли на высоте Н может быть выпол­нен по формуле

Р=Ро,(6 ) где R — радиус Земли, равный 6 370 км.

Пользуясь координатами пунктов, планами (картами) в проекции Гаусса-Крюreра, площади участков Р_пР и размеры получаются всегда больше их горизонтальных проекций, и это увеличение возрастает по мере удаления от осевого меридиана зоны.

Для приведения площади к горизонтальной проекции используют формулу:

2 , (7) где У_m — средняя ордината участка (расстояние от осевого меридиа­на зоны до середины участка).

Приведенный способ изолированных базисов свободен от попра­вок за переход от поверхности референц-эллипсоида и проекции Га­усса-Крюгера, так как координаты точек базисов и границ участков определяются в частной системе, на физической поверхности Земли.

Иногда возникает необходимость получения площадей физиче­ской (топографической) поверхности участка Р_Ф, которая тем боль­ше отличается от площади горизонтального проложения участка Р _г.п, чем больше угол наклона v или уклон i местности. Для получения площади физической поверхности участка его разбивают на части с одинаковыми скатами, т. е. с равностоящими, и более или менее прямыми горизонталями. На каждой из этих частей в перпендику­лярном направлении к горизонталям определяют угол наклона или уклон и вычисляют площадь Р_Ф на физической поверхности земли по следующим формулам:

Р_ф=Р _г.п ;

Р_ф=Р _г.п (8).

Например, уже при угле наклона v = 2,9 (уклоне i = 0,05) поправка составит 1 : 800, или 12,5 м 2 на 1 га.

Требования к точности определения площади земельных участков зависят от многих факторов: хозяйственной значимости (сельскохозяйственные угодья, лесные угодья, городская территория и т. п.), местоположения (центр города, его окраина и т. п.), экологической обстановки (химическая загрязненность земли, атмосферы и т. п.), наличия и ценности недвижимости. Все эти и другие возмож­ные факторы влияют на нормативную стоимость земли, которая в основном и является исходной для расчета требуемой точности оп­ределения площади земельных участков.

Достижение требуемой точности возможно лишь при правильном выборе способа определения площади участка. Очевидно, что наивысшая точность может быть достигнута при аналитическом способе определения площади. При этом способе площадь участка определяется по результатам измерений на местности и погрешность в определении площади зависит от погрешностей этих измерений. Так, погрешность m_p площади треугольника и прямоугольника, вычисляемую по измеренным высоте h с погрешностью т_h и основанию 1 с погрешностью m_i , определяют по формуле (9). При одинаковой относительной погрешности измерения h и l

(10) Например, при Р =1 га (10 000 м 2 ) и 1/S = 1/2 000 т_Р=7 м 2 . Из выражений (23.3) для полигона с п вершинами можно получить фор­мулу погрешности площади вида

где m — средняя квадратическая погрешность определения коорди­нат х и у точек вершин полигона при условии, что

D_i — расстояние от начала координат до i-й точки вершины пол тона (в частном случае — от одной из вершин, принятой за начало координат).

Для прямоугольника со сторонами а и Ь формула (11) примет вид

(12)

а для квадрата со стороной а (13)

Например, если для участка размером 100 х 100 м и площадью 1 га определять координаты со средней квадратической погрешностью 0,02 м, то погрешность площади будет равна 2 м 2 .

Для погрешности площади участка, определяемой по топографическому плану (карте), с учетом погрешностей измерений на м мости и погрешностей составления топографического плана мо использовать формулу следующего вида:

Погрешность m, м 2 , для масштабов

= (14)

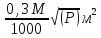
где М -знаменатель численного масштаба плана; Р — площадь участка.

В таблице приведены величины средних квадратических погреш­ностей, вычисленных по формуле (14) для различных площадей участков по планам различных масштабов.

Приведенные формулы являются приближенными, так как не учитывают возможных погрешностей исходных данных и зависимо­сти между входящими в них величинами. Однако они вполне доста­точны для предварительных (проектных) расчетов.

5.4 Понятие о геоинформационных системах

Появление современных высокопроизводительных компьютеров с их возможностью переработки, хранения и выдачи огромного количества информации предопределило возникновение нового направления в хозяйственной и управленческой деятельности челове­ка и новой науки — геоинформатики.

Первоначально понятие «геоинформационные системы» (ГИС) расшифровывалось как «географические информационные системы», поскольку оно появилось в недрах географической науки. Сейчас область использования далеко вышла за пределы географии и приставка «гео» свидетельствует лишь о том, что информация свя­зана с Землей и деятельностью человека на ней.

Таким образом, под геоинформационной системой чаще всего понимают компьютерное хранилище знаний о территориальном взаимодействии природы и общества, обеспечивающее сбор, хранение, обработку и визуализацию (зрительное представление) многих видов информации о явлениях в окружающем человека пространстве и во времени. К их числу относится информация из областей гeографии, информатики, гeодезии, картографии, земельного учета, управления, права, экологии и других наук.

Геоинформационные системы подразделяются:

• по территориальному охвату — на общенациональные и региональные;

• по целям использования – многоцелевые, специализированные, информационно-справочные, для нужд планирования, управления и др;

• по тематике — водных ресурсов, использования земель, лесопользования, туризму и др.

Особенно активно развиваются системы, ориентированные на кадастр.

Источниками информации для ГИС в основном являются гeoгpaфические и топографические карты и планы, аэрокосмические материалы, нормативные и правовые документы.

Современные ГИС, как правило, являются цифровыми и создаются с использованием специального программного обеспечения и объема данных, называемого базой данных.

База данных с цифровой карты включает в себя два варианта информации: пространственную, определяющую местоположение объекта, и семантическую (атрибутивную), описывающую свойства объекта.

Многoобразная пространственная информация в ГИС организуется в виде отдельных тематических слоев, отвечающих решению различных задач. Каждый слой может содержать информацию, относящуюся только к одной или нескольким темам. Например, для задач развития гoродской территории набор из отдельных слоев может включать в себя данные: о землевладениях и недвижимости; об объектах транспорта, образования, здравоохранения, культуры; инженерных сетях; рельефе; геодезических сетях и других объектах городского хозяйства.

Для представления карт и планов в компьютере используется пря­моугольная система координат. Каждая точка описывается одной парой координат: Х, У. Пользуясь координатной системой, можно представить точки, линии и полигоны в виде списка координат. При этом для представления земной поверхности на плоскости используются различные картографические проекции, например проекции Гаусса- Крюгера.

Данные с карты, плана вводятся в компьютер путем цифрования. Цифрование может быть выполнено либо путем оцифровки каждой характерной точки объекта, либо путем сканирования всего листа карты электронным сканером. Ввод в базу данных компьютера может также осуществляться с электронных геодезических приборов. Описательные характеристики объектов могут вводиться с клавиатуры компьютера.

Данные аэро- и космических съемок, записанные в цифровом виде, также могут быть введены в компьютер, минуя бумажную стадию.

5.5 . Геоинформационные системы в кадастре

Любой вид кадастра (земельный, градостроительный, водный лесной и др.) является геоинформационной системой, поскольку содержит совокупность достоверных и необходимых сведений о природном, хозяйственном и правовом положении земель и недр на базе картографической информации. Картографическая информации служит и для оценки количества, качества и стоимости земель, регистрации землепользования и землевладения, текущего контроля за землепользованием.

Информационная основа кадастра создается в результате инвентаризации земель и кадастровых съемок. Эти работы могут охватывать как большие территории (город, район, населенный пункт и т. п.), так и небольшие земельные участки.

Чтобы разместить большое количество сведений в единой информационной системе, кадастровая информация делится на элементарные слои, каждый из которых самостоятельно используется для решения конкретной задачи.

Для автоматизированной системы кадастра, основанной на применении ГИС, используются цифровые кадастровые карты, планы. Все объекты, представленные на кадастровой карте, плане, имею пространственную привязку, т. е. их положение определено в том системе координат, которая принята при создании карты. Описательные данные объекта (земельного участка) составляют содержание базы данных информационной системы. Для обозначения и связи объектов этой базы данных используются идентификаторы (кадастровые номера) участков.

Таким образом, цифровая кадастровая карта, представляя собой совокупность метрических (графических) и семантических (описательных) данных, является картографической частью информационной системы кадастра.

Определяя местоположение земельных участков, их границы площади, она используется как инструмент управления земельными ресурсами.

Таким образом, государственный земельный кадастр является геоинформационной системой, обеспечивая сбор, хранение и в земельной информации потребителям.

Источник

При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.

Основные способы

Существует три основных способа определения площадей:

• аналитический;
• графический;
• механический.

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

S= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
• i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

Sт=0,5*(a+b)*h, где:

• a и b – основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

р=0,5(а+B+c+d), где:

a,b,c,d – величины сторон.

Тогда площадь участка Sу будет равна:

Sy=√(p-a)(p-b)(p-c)(p-d).

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.

Механический способ

Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.

Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность – это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

mp= mt*√ P, где:

• mt – СКП расположения поворотных точек;
• P – площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

mpс= 0,2*√600=4,89 м.

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

Определение площади участка на ПКК

Публичная кадастровая карта (ПКК) – это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).

Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.

Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.

Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: “обл. Московская, р-н Зарайский, снт “Изобретатель”, уч-к 116″.

Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.

Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.

Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.

Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.

По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Аналитический способ

При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.

Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.

Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.

Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)

Выразим площадь каждой трапеции через ее основания и высоту:

Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:

или в общем виде:

В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).

Если при группировке членов выносить за скобки Y1, то получится формула:

Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.

Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.

Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.

Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.

На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.

Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:

Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,

Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:

Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:

mP=an * mt * L, (6.17)

где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин;

его значения:

n 3 4 5 6 7 8 9 10
an 0.204 0.250 0.256 0.250 0.243 0.231 0.222 0.212
n 11 12 15 20 24 30 60 120
an 0.205 0.197 0.179 0.156 0.143 0.128 0.091 0.065

Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.

При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).

Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.

Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.

При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.

Площадь правильного n-угольника можно выразить через его периметр:

И из формулы (6.17) получить формулу относительной ошибки площади:

для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.

Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:

ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.

Источник

ЛЕКЦИЯ № 15

Определение площадей. Геометрические, аналитический

и механический способы

В настоящее время площади земельных угодий и инженерных сооружений вычисляют при помощи компьютеров по исходным данным, полученным в результате измерений на местности, по координатам границ объекта, по данным фотографирования местности и др. Но инженер-геодезист должен знать сущность определения площадей объектов традиционными способами, поскольку их геометрия и математическая основа используется в компьютерных программах и нередки случаи, когда приходится определять площади объектов без применения компьютера. К традиционным относятся способы определения площадей: геометрические, аналитические, механические.

15.1. Геометрические способы определения площади

К геометрическим способам определения площади относятся графические (по чертежам местности) и аналитические (расчетные по координатам контура территории).

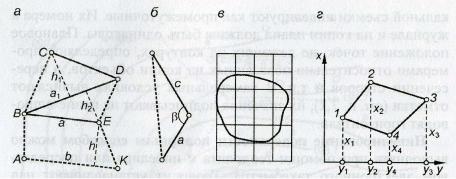
Графические способы определения площади применяются для небольших участков. На местности (рис. 15.1, а ) сложный контур АВСDЕК разделяют на простые геометрические фигуры, вершины которых обозначают вехами. В трапеции АВЕК измеряют основания а и b , высоту h , а в треугольниках ВСD и ВDЕ измеряют основания а 1 и а , высоты h 1 и h . Площадь участка Р = Р 1 + Р 2 + Р 3 , где Р 1 = h ( а

+ b )/2; Р 2 = а 1 h 1 /2; Р 3 = а h 2 /2.

Если треугольнике (рис. 15.1, б ) измерить две стороны и угол β между ними, то

Площадь определяется рассмотренными способами с относительной погреш-

ностью 1 / 1000 – 1/5000.

Рис. 15.1. Геометрические способы определения площадей:

а , б – измерением геометрических фигур; в – с помощью палетки; г – по координатам

Аналогичные способы можно применить для графического определения площади по плану масштаба 1 : М, но с относительной погрешностью 1/50 – 1/1000, зависящей от масштаба и точности плана. С помощью карандаша и линейки контур АВСDЕК (см. рис. 15.1, а ) разграфляют на плане на простые фигуры, а их площади в нашем примере будут вычисляться по формулам, приведенным выше, или по формулам Р 1 = М 2 h ( а + b )/2; Р 2 = М 2 а 1 h 1 /2; Р 3 = М 2 а h 2 /2. Линейные величины а , b и h определяются по плану с погрешностями до 0,5 мм за счет неточностей изображения границ общего контура.

Площадь по плану или карте можно определить при помощи палетки , представляющей прозрачный лист пластика, на который нанесена сетка равных по площади фигур, например квадратов со стороной от 2 до 10 мм (рис. 15.1, в ). Техника определения площади палетками рассмотрена в п. 15.4.

15.2. Аналитический способ определения площад и

Аналитические способы определения площади применяют для замкнутых плоских многоугольников, в которых известны координаты х и у всех вершин (к таким многоугольникам относятся граница населенного пункта, промышленного, сельскохозяйственного или горно-добывающего предприятия, контур лесного массива, озера, болота и т.д.).

Площадь замкнутого многоугольника вычисляют по различным формулам ана-

литической геометрии, наиболее распространены следующие:

2 Р = ∑ х i ( у i +1 – у i -1 );

2 Р = ∑ у i ( х i- 1 – х i +1 ); i = 1, 2, …, n ,

т.е. удвоенная площадь многоугольника равна сумме произведений каждой абсциссы на разность ординат передней и задней по ходу точек, а также сумме произведений каждой ординаты на разность абсцисс задней и передней по ходу точек. Например, для многоугольника 1-2-3-4 (рис. 15.1. г )

2 Р = х 1 ( у 2 – у 4 ) + х 2 ( у 3 – у 1 ) + х 3 ( у 4 – у 2 ) + х 4 ( у 1 – у 3 );

2 Р = у 1 ( х 4 – х 2 ) + у 2 ( х 1 – х 3 ) + у 3 ( х 2 – х 4 ) + у 4 ( х 3 – х 1 );

Площадь вычисляют отдельно по каждой формуле (15.3) с промежуточным контролем разностей координат на условие

∑( у i +1 – у i -1 ) = 0;

∑( х i- 1 – х i +1 ) = 0, i = 1, 2, …, n .

Точность расчетов по формулам (15.4) определяется погрешностями координат. Например, если координаты вершин многоугольника получены теодолитным ходом, то площадь участка получается с относительной погрешностью 1/500 – 1/2000. В случае неверно записанного значения хотя бы одной из координат х i или у i получается ошибочное значение площади при полном совпадении результатов расчетов по формулам (15.3) и (15.4). Такую ошибку можно обнаружить, например, по чрезмерному расхождению между площадью многоугольника и суммой площадей контуров внутри него, нанесенных на план и измеренных планиметром.

15.3. Определение площади полярным планиметром

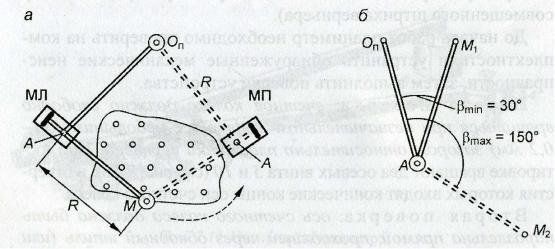
Полярный планиметр – это механическое устройство для определения площади фигур на планах и картах, а также на других чертежах. На полюсном рычаге 1 планиметра (рис. 15.2) закреплен груз с иглой 3 , представляющей полюс О п планиметра. Вторым концом полюсный рычаг шарнирно входит в гнездо 10 корпуса счетного механизма, установленного на обводном рычаге. Обводный шпиль 6 , укреплен-

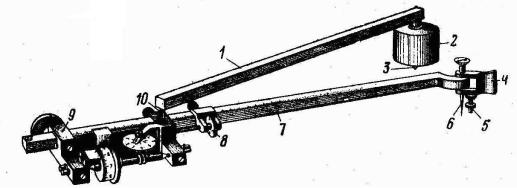
ный на обводном рычаге, представляет обводную точку (марку) М (см. рис. 15.4, б ). Рабочий радиус R обводного рычага равен расстоянию АМ между центром шарнира и обводной точкой М (см. рис. 15.4, а ) . Этот радиус можно изменить перемещением корпуса счетного механизма вдоль обводного рычага (рис. 15.3), а величину радиуса отсчитать по шкале на обводном рычаге и верньеру счетного механизма. В нашем примере (см. рис. 15.3) R = 1713.

Рис. 15.2. Полярный планиметр:

полюсный рычаг; 2 –

груз; 3 – игла; 4 – ручка; 5 – опорный штифт;

— обводный шпиль; 7 –

обводный рычаг; 8 –

опора корпуса счетного механизма; 10 –

гнездо соединения рычагов

Отсчет по шкалам счетного механизма содержит четыре цифры (см. рис. 15.3). Здесь отсчет u = 3684, где 3 – отсчет по циферблату оборотов счетного колеса; 684

– отсчет по шкале счетного колеса относительно нулевого штриха верньера (68 – номер штриха расположенного ниже нуля верньера; 4 – номер совмещенного штриха верньера).

Рис. 15.3. Счетный механизм планиметра:

1 – указатель; 2 – счетное колесо; 3 – верньер счетного механизма; 4 – винты регулировки зазора между верньером и сетным колесом; 5, 10 – винты регулировки счетного колеса; 6 – опорный ролик; 7 – верньер шкалы радиуса планиметра; 8 – закрепительный винт корпуса счетного механизма; 9 – гнездо соединения рычагов; 11 – циферблат счетчика оборотов счетного колеса

П о в е р к и п л а н и м е т р а

До начала работ планиметр необходимо проверить на комплектность и устранить обнаруженные механические неисправности, затем выполнить следующие поверки устройства:

1. Счетное колесо должно свободно вращаться при незначительном люфте и

с небольшим (0,1 – 0,2 мм) зазором относительно пластинки верньера . При юсти-

ровке вращают два осевых винта 5 и 10 (см. рис. 15.3), в отверстия которых входят конические концы оси счетного колеса.

2. Ось счетного колеса должна быть параллельна прямой, проходящей через обводный шпиль(или метку) и центр шарнира . Для поверки контур обводят шпи-

лем (маркой М ) несколько раз в положении планиметра МЛ «счетный механизм слева от фигуры» (см. рис . 15.5, а ) и столько же раз в положении МП «счетный механизм справа от фигуры», не меняя точки полюса О . Если средние разности отсчетов n МЛ и n МП различаются в пределах точности измерений планиметром, то

условие считается выполненным. Для юстировки исправительным винтом изменяют угол между корпусом счетного механизма и обводным рычагом.

Рис. 15.4. Вторая поверка планиметра ( а ); допустимые углы между рычагами ( б )

При работе с неотъюстированным на данное условие планиметром каждую фигуру следует обводить при двух положениях планиметра – ПП и ПЛ и за окончательный результат принимать среднее.

Для измерения площади план кладут на расположенную горизонтально чертежную доску с гладкой поверхностью. Полюс полярного планиметра можно закреплять на плане в положении вне контура или в положении внутри контура , предпочтительное положение полюса – вне контура. Выбирают положение полюса так, чтобы при обводе контура угол β между рычагами (см. рис. 15.4, б ) не был меньше 30 и больше 150°. Обводную точку М совмещают с какой-либо точкой К контура. По счетному механизму берут отсчет u 1 и записывают в таблицу 15.1, затем контур плавно обводят точкой М и завершают обвод в точке К и берут отсчет u 2 (желательно обводить против часовой стрелки, в этом случае последовательные значения отсчетов u i уменьшаются и это удобно для вычислений). Разность отсчетов u 1 – u 1 = n 1 представляет площадь в делениях планиметра.

Продолжают обводы, берут отсчеты u i (см. табл. 15.1) и вычисляют разности отсчетов n i , которые не должны различаться между собой более чем на две единицы при n ≤ 200, на четыре при n ≤ 1000, на шесть при n ≤ 2000. Вычисляют среднюю площадь n в делениях планиметра.

Если плюс расположен вне фигуры, ее площадь в масштабе плана вычисляется по формуле

Источник

При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.

Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) – рис.6.2.

Рис.6.2

Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.

Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)

P=PI+PII-PIII.                                          (6.9)

Выразим площадь каждой трапеции через ее основания и высоту:

PI=0.5(X1+X2)*(Y1-Y2);
PI=0.5(X2+X3)*(Y3-Y2);                      (6.10)
PI=0.5(X3+X1)*(Y1-Y3);

Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:

2*P=X1*(Y2-Y3)+X2*(Y3-Y1)+X3*(Y1-Y2)

или в общем виде:

(6.11)

В этой формуле индекс “i” показывает номер вершины треугольника; индекс “i” означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).

Если при группировке членов выносить за скобки Y1, то получится формула:

(6.12)

Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.

Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n – угольника.

Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n – угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.

Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.

На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.

Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:

(6.13)

(6.14)

Рис.6.3

Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой – сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,

(6.15)

где

c = Sin( β/2 ) .

Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:

или

(6.16)

Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:

mP=an * mt * L,                    (6.17)

где: L – периметр многоугольника,
an – коэффициент, зависящий от n – количества вершин;

его значения:

n    3    4     5    6    7     8    9    10
an    0.204     0.250    0.256     0.250     0.243    0.231     0.222     0.212
n    11    12     15    20    24     30    60    120
an    0.205     0.197    0.179     0.156     0.143    0.128     0.091     0.065

Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n – угольника. Так, если площадь неправильного n – угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.

При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).

Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.

Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.

При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.

Площадь правильного n-угольника можно выразить через его периметр:

(6.18)

И из формулы (6.17) получить формулу относительной ошибки площади:

(6.19)

где

(6.20)

Например:

для треугольника (n=3) mp/P = 4.24* mt/L,
для четырехугольника (n=4) mp/P = 4.00* mt/L,
для пятиугольника (n=5) mp/P = 3.72 mt/L,
для шестиугольника (n=6) mp/P = 3.46 mt/L.

Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:

mp/P=4* mt/L;           (6.21)

ошибка этой формулы может достигать 15% – 20% для участков, форма которых заметно отличается от формы правильного n -угольника.