Как найти площадь антенны – Сайт, где вы сможете решить свои вопросы

Diagram

Антенна собирает энергию падающего на нее потока мощности электромагнитного излучения. A — геометрическая площадь, A_e — эффективная площадь, E — электрическое поле, H — магнитное поле Иллюстрация для калькулятора

Калькулятор позволяет определить эффективную площадь антенны A_e для заданной частоты f или длины волны λ и коэффициента усиления антенны G. Этот и другие калькуляторы на TranslatorsCafe.com пригодятся не только инженерам и студентам технических специальностей, но и всем, кто хочет изучить технический английский, так как все они есть и в английской версии.

Пример: Рассчитать эффективную площадь антенны радиотелескопа РТ-70 в Крыму: коэффициент усиления его антенны 69,5 дБи или 9000000, рабочая частота 5,0 ГГц (или длина волны 6 см).

Входные данные

Частота

или Длина волны

Коэффициент усиления антенны, линейный

или Коэффициент усиления антенны, dBd

G дБ

или Коэффициент усиления антенны, dBi

G дБ

Поделиться ссылкой на этот калькулятор, включая входные параметры

Выходные данные

Эффективная площадь антенны

A_e м²

Для расчета введите величины в соответствующие поля, выберите единицы и нажмите на кнопку Рассчитать.

Эффективная площадь антенны представляет собой площадь эквивалентной плоской антенны с равномерным амплитудно-фазовым распределением и максимальным коэффициентом направленного действия (КНД), равным КНД рассматриваемой антенны. С этой площади антенна, направленная на источник сигнала, поглощает энергию падающего электромагнитного излучения. Для удобства объяснения рассмотрим эффективную площадь приемной антенны. Поглощенная антенной мощность P определяется как

P = P_d A

Здесь P_d —плотность потока мощности (удельная мощность на единицу поверхности) падающей электромагнитной энергии и A — площадь раскрыва (геометрическая площадь) антенны. Коэффициент усиления антенны G прямо пропорционален геометрической площади антенны A. Его можно увеличить путем фокусирования излучения только в одном направлении с одновременным уменьшением излучения во всех остальных направлениях. Поэтому чем ýже ширина пучка, тем выше коэффициент усиления антенны. Соотношение между коэффициентом усиления антенны и ее площадью выражается формулой, в которую также входит КПД антенны:

Formula

или

Formula

Здесь λ — длина волны и η — КПД антенны, который всегда меньше единицы:

Formula

Здесь A_e — эффективная площадь (апертура) антенны, которая определяется как физическая площадь антенны, умноженная на КПД антенны. Если КПД антенны равен 1 (или 100%), это означает, что вся энергия, подаваемая передатчиком в передающую антенну излучается в пространство. Если же это приемная антенна, то при единичном КПД вся энергия, принимаемая антенной, попадает в приемник. Однако на практике часть энергии всегда теряется в форме тепловой энергии, которая расходуется на разогрев элементов конструкции антенны и фидера.

Заменяя произведение площади на КПД Aη на эффективную площадь A_e, получаем:

Formula

или

Formula

Эта формула и используется в данном калькуляторе. Из нее видно, что для заданной эффективной площади антенны ее коэффициент усиления возрастает с квадратом длины волны или при постоянной длине волны коэффициент усиления антенны прямо пропорционален ее эффективной площади. Отметим, что для апертурных антенн, таких как рупорные или параболические, эффективная площадь связана с геометрической площадью и всегда меньше этой площади. Однако, для проволочных антенн (например, симметричных и несимметричных вибраторов, антенн типа «волновой канал»), эффективная площадь обычно значительно (иногда в десятки раз) больше физической площади антенны.

Радиотелескоп РТ-70 в 2 км от пос. Молочное (Сакский район, Крым, Россия). Эффективная площадь его антенны составляет только 67% от геометрической площади антенны.

Коэффициент усиления (КУ) антенны по мощности G, называемый обычно просто коэффициентом усиления, представляет собой отношение мощности излучения направленной антенны к мощности, излучаемой идеальной ненаправленной антенной, причем ко входам обеих антенн подводится одинаковая мощность. Коэффициент усиления — величина безразмерная, но чаще она выражается в децибелах (дБ, отношение по мощности) или изотропных децибелах (дБи, dBi, также отношение по мощности). Изотропный децибел характеризует коэффициент усиления антенны по сравнению с идеальной изотропной антенной, равномерно излучающей энергию во всех направлениях.

Например, определим эффективную площадь российского телескопа РТ-70, который находится в Крыму неподалеку от Евпатории.

Эффективная площадь (апертура) антенны типа «волновой канал». Отметим, что, в отличие от любой параболической антенны, эффективная площадь которой всегда меньше ее физической площади, эффективная площадь антенны «волновой канал» всегда значительно больше физических размеров антенны. Эллипс эффективной площади расположен перпендикулярно траверсе. Отметим также, что чем выше коэффициент усиления антенны, тем больше ее эффективная площадь. Антенна с большим числом элементов и более длинной траверсой имеет больший КУ и бóльшую эффективную площадь.

Коэффициент усиления антенны G = 69,5 дБи или 9 000 000.

Диаметр антенны d = 70 м.

Рабочая частота f = 5,0 ГГц (6 см).

Геометрическая площадь антенны A = πD²/4 = π70²/4 = 3848 м². В то же время, ее эффективная площадь равна

Formula

Как мы видим, эффективная площадь составляет только 67% от геометрической площади антенны.

Теперь рассчитаем эффективную площадь 5-элементной антенны типа «волновой канал» (также называемой по именам японских изобретателей антенна Яги-Уда, антенна Уда-Яги или просто антенна Яги), работающей на частоте 500 МГц и имеющей коэффициент усиления 40 дБи, который соответствует безразмерному коэффициенту усиления 10. Длина активного элемента несколько меньше половины длины волны 0,5λ = 30 см, где λ = 60 см — длина волны.

Formula

Диаметр круга площадью 0,28 кв. м определяется как

Эта телевизионная антенна состоит из двух антенн: антенны дециметрового диапазона типа «волновой канал» с 18 директорами и уголковым рефлектором с КУ=14 дБи (справа) и логопериодической антенны с V-образными элементами метрового диапазона (слева)

Formula

То есть, для активного элемента длиной около 0.5λ = 30 см мы получаем круг диаметром 60 см (точнее, эллипс).

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 октября 2013 года; проверки требуют 6 правок.

Эффективная площадь антенны — площадь эквивалентной плоской антенны с равномерным амплитудно-фазовым распределением, обладающей тем же максимальным значением коэффициента направленного действия, что и данная антенна.

Для антенны в режиме приема эффективная площадь антенны (используется также термин эффективная поверхность антенны) характеризует способность антенны собирать (перехватывать) падающий на неё поток мощности электромагнитного излучения и преобразовывать этот поток мощности в мощность на нагрузке (с точностью до КПД антенны и качества согласования антенны с нагрузкой).

Эффективная площадь антенны

${displaystyle A_{eff}={frac {P}{Pi }}}$ , где

$P$ , Вт — максимально возможная мощность, выделяемая в нагрузке данной антенны; $Pi$ , Вт/м² — плотность потока мощности плоской волны в месте расположения антенны. Эффективная площадь антенны как коэффициент пропорциональности между P и П аналогична действующей высоте антенны как коэффициенту пропорциональности между амплитудой напряженности электрического поля [В/м] падающей на антенну плоской волны и амплитудой ЭДС [В] на клеммах антенны.

Из-за неравномерного амплитудно-фазового распределения и дифракции радиоволн на антенне эффективная площадь антенны всегда меньше её геометрической площади (площади апертуры антенны). Электромагнитные волны со слишком большой (по сравнению с размерами антенны) длиной волны огибают антенну, при слишком короткой длине волны сказываются погрешности изготовления антенны. Поэтому считается, что рабочий диапазон длин волн λ антенны ${displaystyle 20sigma <lambda <{frac {1}{20}}D}$ , где $sigma$ — погрешность выполнения поверхностей антенны, $D$ — диаметр апертуры. За границами этого диапазона длин волн эффективная площадь антенны резко падает^[1].

Отношение эффективной площади антенны к геометрической площади антенны называется коэффициентом использования поверхности (КИП) антенны. То есть эффективная площадь антенны пропорциональна площади апертуры антенны и КИП. Для максимизации энергетических характеристик (КНД) антенна проектируется таким образом, чтобы её эффективная площадь была максимальной, что при ограничении на площадь апертуры антенны (при ограничении на габаритные размеры антенны) достигается максимизацией КИП. Для этого стремятся обеспечить равномерное амплитудно-фазовое распределение.

Эффективная площадь связана с диаграммой направленности (ДН) антенны и её КНД:

${displaystyle A_{eff}={frac {lambda ^{2}}{Omega _{a}}}=D_{0}{frac {lambda ^{2}}{4pi }}}$ , где

${displaystyle Omega _{a}=int limits _{4pi }A(theta ,varphi )dOmega }$

— эффективный телесный угол; ${displaystyle A(theta ,varphi )}$ — нормированная к своему максимуму ДН антенны; $D_0$ — максимальное значение КНД антенны.

Коэффициент использования апертуры[править | править код]

Коэффициентом использования апертуры называется безразмерная величина, равная отношению эффективной площади антенны к её геометрической площади:

${displaystyle varepsilon ={frac {A_{eff}}{A_{geom}}}}$

Так как эффективная площадь антенны всегда меньше геометрической, коэффициент использования апертуры лежит в диапазоне от 0 до 1.

Примечания[править | править код]

↑ Конникова В.К., Лехт Е.Е., Силантьев Н.А. Практическая радиоастрономия. — М.: Издательство МГУ, 2011. — 304 с. — ISBN 978-5-211-05938-2.

См. также[править | править код]

КПД антенны
Коэффициент усиления антенны

Источник

F (θ,ϕ) =1. С уче-

редачи без изменения характеристик и параметров. Это позволяет использовать в импульсных РЛС одну и ту же антенну на передачу и прием.

Дополнительно вводятся параметры, характеризующие специфику работы антенн на прием. К ним относятся:

мощность, отдаваемая в нагрузку; поляризационная эффективность; шумовая температура; эффективная площадь антенны;

коэффициент использования площади.

Последние два параметра относятся и к передающим антеннам, но их удобнее рассматривать применительно к приемным.

Мощность, отдаваемая антенной в нагрузку (т.е. приемнику) на основании эквивалентной схемы (см. рис. 1.10) выражается равенством:

P =	I 2RH	=	e2		RH .	(1.26)

H	2		Zвх + ZH	2	2

Подставляя в (1.26) значения ЭДС е из формулы (1.20), получим:

λ2

RΣ Dmax F 2

(θ,ϕ)

RH .

(1.27)

π2

Zвх + ZH

120

Максимальная мощность выделяется в нагрузке, если обеспечивается полное согласование входного сопротивления антенны с сопротивлением нагрузки ( X H = −X вх; RH = Rвх ) и совмещение максимума ДНА с направле-

нием на источник излучения. При этом Zвх + ZH = 2Rвх , том этих условий из выражения (1.9) получим:

λ2E2

R D

λ2

max

вх =

π2

240π

4π

H max

120

max R

Rвх

вх

Учитывая, что RΣ Rвх =ηA – КПД антенны, окончательно находим:

P	=	E2		λ2	D	η	.	(1.28)
240π	4π
H max			max		A

Как видно из (1.28), чем выше направленные свойства антенны, тем большую мощность она извлекает из поля.

1.2.4.Эффективная площадь антенны

Ввыражении (1.28) первый сомножитель представляет собой плотность потока мощности в точке приема, так как П = E2 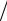240π , а произведе-

ние λ2 D	max	4π имеет размерность площади и называется эффективной

площадью антенны:
		S	эфф	=	λ2	D .	(1.29)
		4π
Из (1.29) следует, что		max

		PH max = ПSэффηA .	(1.30)

Под эффективной площадью антенны следует понимать такую условную площадку, которая, будучи помещена вместо реальной антенны в ту же точку пространства нормально к направлению падающей волны и не имея потерь, создает на входе приемника такую же мощность, что и согласованная с ним антенна.

Эффективная площадь антенны меньше ее геометрической площади Sг. Отличия геометрической и эффективной площадей антенны объясняются тем, что в реальной антенне часть падающей на нее мощности переизлучается и рассеивается, т.е. полезно используется не вся перехваченная у поля мощность, а только ее часть, хотя и бόльшая. Условная идеальная площадка не имеет потерь, поэтому ее площадь может быть меньше для создания такой же мощности на входе приемника. Формула (1.30) является одной из важнейших в теории антенн. Она связывает эффективную площадь антенны с ее КНД и пригодна для любой антенны.

1.2.5. Коэффициент использования площади антенны

Коэффициент использования площади антенны (КИП) является показателем эффективности использования площади реальной антенны, численно

определяется отношением
ξA = Sэфф Sг	(1.31)

и изменяется в пределах 0 ≤ξA ≤1.

Из соотношений (1.29) и (1.31) можно получить практические формулы для расчета коэффициента усиления и КНД:

4π

эфф

4π

;

(1.32)

max

Gmax =

4π

Sэфф ηA

4π

Sг ξA ηA .

(1.33)

Произведение КИП на КПД называется коэффициентом эффективно-

сти антенны:

gA = ξA ηA .

(1.34)

Коэффициент поляризационной эффективности. Мощность, выделяе-

мая в нагрузке приемной антенны, зависит также от согласования поляризационных параметров принимаемой волны и приемной антенны.

Для оценки эффективности приема сигналов различной поляризации вводится коэффициент поляризационной эффективности Кпэ. Он равен отношению мощности, выделяемой в нагрузке приемной антенны, к мощности, которая выделялась бы в нагрузке при условии полного согласования поляризационных параметров источника и приемной антенны.

Полное согласование поляризационных параметров обеспечивается,

когда Kэ1 = Kэ2 ;	γ1 =γ2 ;	sgn Kэ1 = sgn Kэ2 , где индексы 1 и 2 соот-
ветствуют приемной антенне и источнику излучения соответственно.
Коэффициент поляризационной эффективности определяется выраже-
нием:
K	nэ	=	1		1+	4Kэ1Kэ2	+(1− Kэ21)(1− Kэ22 ) cos(γ1	−γ2 )	. (1.35)

	2			(1+ Kэ21)(1+ Kэ22 )

Кпэ изменяется в пределах от 0 до 1. Управляя поляризацией антенны, можно получать максимум полезного сигнала и (или) минимум помехи.

Шумовая температура приемной антенны. В антенне и волноводном тракте возникают внутренние шумы, вызванные тепловым движением электронов. К ним добавляются внешние шумы, принятые антенной из пространства. Они обусловлены грозовыми разрядами, индустриальными помехами, радиоизлучением Солнца, а также тепловым радиоизлучением земной поверхности и атмосферы.

Суммарную мощность шумов антенно-волноводного тракта в полосе пропускания приемника F можно оценить по формуле:

где k =1,38 10−23 Вт/Гц К – постоянная Больцмана, ТА – эквивалентная шумовая температура антенны по абсолютной шкале.

Так как шум антенно-волноводного тракта включает в себя внутренние и внешние составляющие, то и эквивалентную шумовую температуру ТА

также можно представить в виде суммы:
TA = TA B + TA И ,	(1.37)

где ТАВ – шумовая температура, связанная с внутренними шумами; ТАИ – шумовая температура антенны, определяемая внешними источниками.

Шумовая температура ТАВ оказывается довольно просто связанной с

КПД антенно-волноводного тракта ηАВ:
TA B = T0 (1 −ηAB ) ,	(1.38)

где Т0=288 К – стандартная температура среды.

Согласно выражению (1.38), увеличение КПД антенно-волноводного тракта снижает шумовую температуру ТАВ. При этом ТАВ≤Т0.

Шумовая температура ТАИ зависит от пространственного распределения источников внешних помех и направленных свойств антенны. В метровом диапазоне волн антенны имеют широкую ДН, и в результате ТАВ<<ТАИ. При этом ТА≥50…100 К.

В сантиметровом и дециметровом диапазонах в силу остронаправленности антенн ТА=5…20 К. В этих диапазонах необходимо максимизировать КПД. При ηA = 0,9…0,95, согласно (1.38), имеем ТАВ=30…15 К, что сравнимо с ТАИ.

Источник

Параметры антенн

ширина луча

уровень боковых
лепестков

уровень заднего
лепестка

Рисунок 1. Диаграмма направленности антенны в полярных координатах

Параметры антенн

Коэффициент усиления и коэффициент направленного действия

Благодаря особой конструкции антенны обеспечивают сосредоточение плотности излучения в определенных пространственных направлениях.
Мерой направленности антенны без потерь является
коэффициент усиления антенны.
Этот параметр тесно связан с коэффициентом направленного действия антенны.
Однако, в отличие от коэффициента направленного действия, который характеризует только направленные свойства антенны,
коэффициент усиления учитывает также и эффективность антенны.
Следовательно, он позволяет оценить фактическую излучаемую мощность.
Она, очевидно, является несколько меньшей, чем мощность, подводимая к антенне от передатчика.
Поскольку эту мощность легче измерить, чем оценить направленность антенны,
коэффициент усиления антенны используется чаще, чем коэффициент направленного действия.
Если же предположить, что рассматривается антенна без потерь, то можно считать,
что коэффициент направленного действия приблизительно равен коэффициенту усиления антенны.

Для определения коэффициента усиления антенны используется физическая абстракция
— изотропная антенна.
В большинстве случаев в этом качестве рассматривается гипотетический всенаправленный или изотропный излучатель
(то есть излучающий во всех направлениях) без потерь.
Иногда вместо него может рассматриваться
дипольная антенна,
которая тоже может считаться всенаправленной, по крайней мере, в одной плоскости.

Для измеряемой антенны в некоторой точке на определенном расстоянии от нее измеряется плотность мощности излучения
(мощность на единицу площади) и сравнивается со значением, полученным при использовании изотропной антенны при прочих равных условиях.
Отношение этих двух измеренных плотностей мощности будет равно коэффициенту усиления антенны (в данном направлении).

Например, если направленная антенна порождает в заданной точке плотность мощности, в 200 раз большую, чем изотропна антенна,
то ее коэффициент усиления G равен 200 или
23 дБ.

Диаграмма направленности антенны

Диаграммой направленности антенны
называют графическое представление пространственного распределения излучаемой антенной энергии.
В зависимости от назначения, к антеннам могут предъявляться требования принимать сигналы только с определенного направления и
не принимать с других направлений (например, телевизионная антенна, радиолокационная антенна) или,
напротив, принимать сигналы со всех возможных направлений.

Желаемый коэффициент направленного действия достигается целенаправленным конструированием антенны,
включающим в себя проектирование электрических и механических свойств.
Коэффициент направленного действия показывает, насколько хорошо антенна принимает или излучает в определенном направлении.
Он отображается в графическом представлении (в виде диаграммы направленности антенны)
в функции азимута (горизонтальная диаграмма направленности) и
угла места
(вертикальная диаграмма).

ширина луча

уровень боковых
лепестков

уровень заднего
лепестка

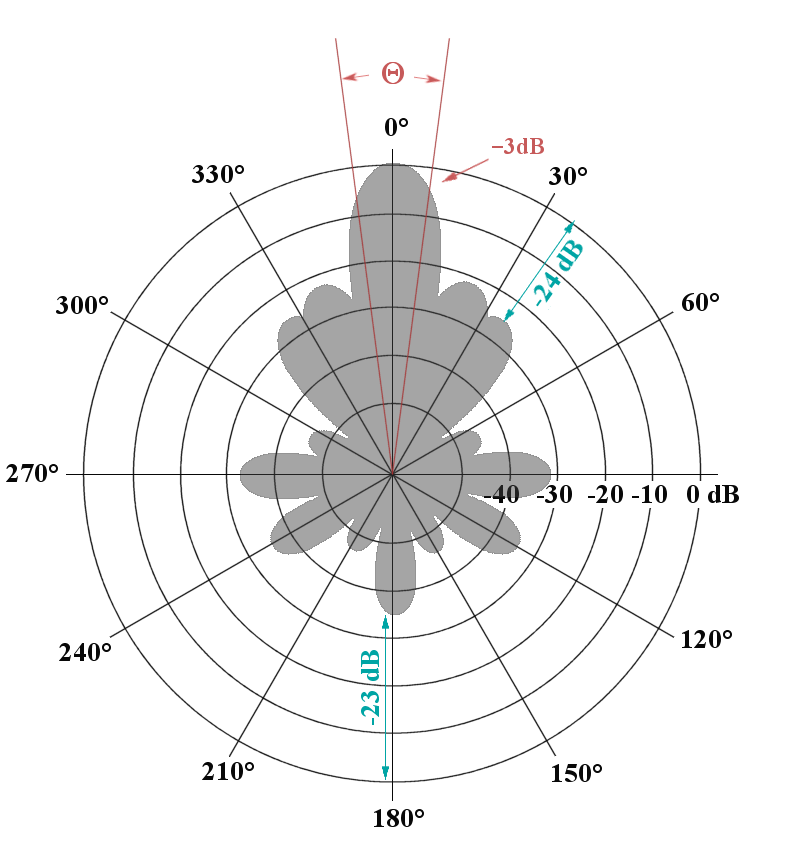
Рисунок 2. Та же диаграмма направленности антенны в прямоугольных координатах

ширина луча

уровень боковых
лепестков

уровень заднего
лепестка

Рисунок 2. Та же диаграмма направленности антенны в прямоугольных координатах

Для отображения может использоваться как прямоугольная (Декартова) система координат, так и полярная.
Измеренные значения могут откладываться в линейном или в логарифмическом масштабе.

Ширина луча по уровню половинной мощности

Ширина луча по уровню половинной мощности
есть угловой размер диаграммы направленности, в котором излучается как минимум половина максимальной мощности.
Точки на диаграмме направленности, соответствующие границам ее основного лепестка, являются точками,
в которых напряженность излучаемого антенной поля уменьшается на 3 дБ по сравнению с максимальной.
Угол Θ между этими двумя точками называют углом апертуры или шириной луча по уровню половинной мощности.
Чтобы упростить вычисления, иногда предполагают,
что излучаемая мощность равномерно распределена в пределах этого угла и равна нулю за его пределами.

Телесный угол луча

Телесным углом называют двумерный угол.
Его принято обозначать переменной Ω, а единицей измерения является стредиан [Sr].
Пространственный угловой размер луча антенны Ω_A определяется как телесный угол,
в пределах которого будет излучаться вся мощность при условии, если интенсивность излучения постоянна
(и равна максимальному значению) для всех углов в пределах Ω_A.
Это сугубо теоретическая величина, которая,
однако, может приближенно характеризовать антенны с очень высокой направленностью и малыми боковыми лепестками:

Ω_A ≈ Θ_az·Θ_el

где:

Θ_az = ширина луча по уровню половинной мощности в горизонтальной плоскости;
Θ_el = ширина луча по уровню половинной мощности в вертикальной плоскости.

(1)

Применяются разные модели пространственного представления луча: модель, где сечение луча плоскостью,
перпендикулярной его оси, имеет прямоугольную форму со сторонами,
длины которых соответствуют ширине луча в горизонтальной и вертикальной плоскостях,
а также модели, в которых это сечение имеет круговую или эллиптическую форму (каноническое представление пространственного угла).

Уровень бокового излучения

Кроме основного лепестка диаграмма направленности антенны имеет еще несколько боковых лепестков и задний лепесток.
Эти явления нежелательны, поскольку они негативно влияют на направленные свойства антенны и отбирают энергию из основного лепестка.
Как правило, оценивается отношение между уровнем основного лепестка и наибольшего бокового лепестка диаграммы направленности.
При проектировании и эксплуатации антенн нужно стремиться к тому, чтобы это отношение было как можно большим.

Уровень заднего излучения

Для оценки антенн продольного излучения используют такой показатель как относительный уровень заднего излучения.
В англоязычной литературе используется обозначение F/B (front / back).
Он определяется как отношение величины основного лепестка в направлении главного максимума излучения
(то есть в направлении 0º) к величине заднего лепестка в направлении 180º.
Нужно стремиться, чтобы это отношение также было как можно больше.

Рисунок 3. Апертура антенны — это часть сферической поверхности

Апертура антенны — это часть сферической поверхности,
(нажмите для увеличения: 600·400 пиксель = 14 килобайт)

Рисунок 3. Апертура антенны — это часть сферической поверхности

Эффективная площадь антенны

Важным параметром является эффективная площадь антенны или «апертура антенны», обозначаемая символом A_e.
При условии оптимальной ориентации антенны и поляризации волны максимальная мощность,
которая может быть получена на выходе приемной антенны, пропорциональна плотности мощности электромагнитной волны, падающей в точку приема.
Эта плотность мощности представляет собой количество мощности на единицу площади.
Таким образом, коэффициент пропорциональности между мощностью на выходе антенны и
плотностью мощности падающей электромагнитной волны имеет значение площади антенны в электромагнитном поле.
Эту площадь называют эффективной площадью антенны A_e.
Она тесно связана с коэффициентом направленного действия антенны D,
который, в свою очередь, равен коэффициенту усиления антенны в случае отсутствия в ней потерь:

D = G·η =	4π · A_e	; A_e = K_a·A	где:	η = эффективность антенны; λ = длина волны; A_e = эффективная площадь антенны; A = геометрическая площадь антенны; K_a = коэффициент апертуры.	(2)

λ²

Эта формула показывает очень важное свойство: характеристики направленности антенны определяются ее площадью.
Чем больше диаметр антенны по отношению к длине волны, тем выше ее направленность.

Эффективная площадь антенны может также быть определена для линейных антенн.
Она не обязательно будет соответствовать геометрическим размерам антенны, что особенно видно на примере проволочных антенн.
Соотношение между этими двумя величинами называют коэффициентом апертуры K_a.
Для антенн с большими параболическими зеркалами принимают, что K_a = 0,6 … 1.
Эффективная площадь антенны для прямоугольного рупорного облучателя со
сторонами a и b
немного меньше геометрической площади его раскрыва a·b.

Эффективная площадь антенны зависит от распределения в раскрыве антенны (по ее поверхности).
Если это распределение является линейным, то K_a= 1.
Однако такая высокая эффективность апертуры при линейном распределении поля в раскрыве приводит к возрастанию боковых лепестков.
Если для практического использования антенны требуется обеспечить низкий уровень боковых лепестков,
то распределение поля не должно быть линейным, но тогда эффективная площадь антенны будет меньше,
чем ее геометрическая площадь (A_e< A).

Полоса частот антенны

Полосой частот антенны называют диапазон рабочих частот,
в пределах которого антенна еще сохраняет требуемые характеристики, такие как:

диаграмма направленности (пространственное распределение излучаемого поля);
поляризация;
сопротивление (импеданс);
режим распространения.

Большинство антенных технологий обеспечивают работу в полосе частот,
которая составляет 5 … 10% от центральной частоты, в силу того, что антенна представляет собой резонансное устройство.
Например, для центральной частоты 2 ГГц полоса частот будет составлять 100 … 200 МГц.
Для достижения широкополосной работы требуется применение антенн специальных типов
(например,
логопериодическая дипольная антенна,
щелевая антенна с коническими щелями).

Источник

From Wikipedia, the free encyclopedia

In electromagnetics and antenna theory, the aperture of an antenna is defined as “A surface, near or on an antenna, on which it is convenient to make
assumptions regarding the field values for the purpose of computing fields at external points. The aperture is often taken as that portion of a plane surface near the antenna, perpendicular to the direction of maximum radiation, through which the major part of the radiation passes.”^[1]

Effective area[edit]

The effective area of an antenna is defined as “In a given direction, the ratio of the available power at the terminals of a receiving antenna to the power flux density of a plane wave incident on the antenna from that direction, the wave being polarization matched to the antenna.”^[1] Of particular note in this definition is that both effective area and power flux density are functions of incident angle of a plane wave. Assume a plane wave from a particular direction $(theta ,phi )$ , which are the azimuth and elevation angles relative to the array normal, has a power flux density ${displaystyle |{vec {S}}|}$ ; this is the amount of power passing through a unit area normal to the direction of the plane wave of one square meter.

By definition, if an antenna delivers ${displaystyle P_{text{O}}}$ watts to the transmission line connected to its output terminals when irradiated by a uniform field of power density ${displaystyle |S(theta ,phi )|}$ watts per square meter, the antenna’s effective area $A_{{text{e}}}$ for the direction of that plane wave is given by

${displaystyle A_{text{e}}(theta ,phi )={frac {P_{O}}{|{vec {S}}(theta ,phi )|}}.}$

The power ${displaystyle P_{text{O}}}$ accepted by the antenna (the power at the antenna terminals) is less than the power ${displaystyle P_{text{R}}}$ received by an antenna by the radiation efficiency $eta$ of the antenna.^[1] ${displaystyle P_{text{R}}}$ is equal to the power density of the electromagnetic energy ${displaystyle |S(theta ,phi )|=|{vec {S}}cdot {hat {a}}|}$ , where ${hat {a}}$ is the unit vector normal to the array aperture, multiplied by the physical aperture area $A$ . The incoming radiation is assumed to have the same polarization as the antenna. Therefore,

${displaystyle P_{text{O}}=eta P_{text{R}}=eta A|{vec {S}}cdot {hat {a}}|=eta A|{vec {S}}(theta ,phi )|cos theta cos phi ,}$

and

${displaystyle A_{text{e}}(theta ,phi )=eta Acos theta cos phi .}$

The effective area of an antenna or aperture is based upon a receiving antenna. However, due to reciprocity, an antenna’s directivity in receiving and transmitting are identical, so the power transmitted by an antenna in different directions (the radiation pattern) is also proportional to the effective area $A_{e}$ . When no direction is specified, $A_{e}$ is understood to refer to its maximal value.^[1]

Aperture efficiency[edit]

In general, the aperture of an antenna cannot be directly inferred from its physical size.^[2] However so-called aperture antennas such as parabolic dishes and horn antennas, have a large (relative to the wavelength) physical area ${displaystyle A_{text{phys}}}$ which is opaque to such radiation, essentially casting a shadow from a plane wave and thus removing an amount of power ${displaystyle A_{text{phys}}S}$ from the original beam. That power removed from the plane wave can be actually received by the antenna (converted into electrical power), reflected or otherwise scattered, or absorbed (converted to heat). In this case the effective aperture $A_{e}$ is always less than (or equal to) the area of the antenna’s physical aperture ${displaystyle A_{text{phys}}}$ , as it accounts only for the portion of that wave actually received as electrical power. An aperture antenna’s aperture efficiency ${displaystyle e_{text{a}}}$ is defined as the ratio of these two areas:

${displaystyle e_{text{a}}={frac {A_{e}}{A_{text{phys}}}}.}$

The aperture efficiency is a dimensionless parameter between 0 and 1 that measures how close the antenna comes to using all the radio wave power intersecting its physical aperture. If the aperture efficiency were 100%, then all the wave’s power falling on its physical aperture would be converted to electrical power delivered to the load attached to its output terminals, so these two areas would be equal: ${displaystyle A_{text{e}}=A_{text{phys}}}$ . But due to nonuniform illumination by a parabolic dish’s feed, as well as other scattering or loss mechanisms, this is not achieved in practice. Since a parabolic antenna’s cost and wind load increase with the physical aperture size, there may be a strong motivation to reduce these (while achieving a specified antenna gain) by maximizing the aperture efficiency. Aperture efficiencies of typical aperture antennas vary from 0.35^{[citation needed]} to well over 0.70.

Note that when one simply speaks of an antenna’s “efficiency”, what is most often meant is the radiation efficiency, a measure which applies to all antennas (not just aperture antennas) and accounts only for the gain reduction due to losses. Outside of aperture antennas, most antennas consist of thin wires or rods with a small physical cross-sectional area (generally much smaller than $A_{{text{e}}}$ ) for which “aperture efficiency” is not even defined.

Aperture and gain[edit]

The directivity of an antenna, its ability to direct radio waves preferentially in one direction or receive preferentially from a given direction, is expressed by a parameter $G$ called antenna gain. This is most commonly defined as the ratio of the power ${displaystyle P_{text{o}}}$ received by that antenna from waves in a given direction to the power ${displaystyle P_{text{iso}}}$ that would be received by an ideal isotropic antenna, that is, a hypothetical antenna that receives power equally well from all directions.^{[Note 1]} It can be seen that (for antennas at a given frequency) gain is also equal to the ratio of the apertures of these antennas:

${displaystyle G={frac {P_{text{o}}}{P_{text{iso}}}}={frac {A_{text{e}}}{A_{text{iso}}}}.}$

As shown below, the aperture of a lossless isotropic antenna, which by this definition has unity gain, is

${displaystyle A_{text{iso}}={frac {lambda ^{2}}{4pi }},}$

where $lambda$ is the wavelength of the radio waves. Thus

${displaystyle G={frac {A_{text{e}}}{A_{text{iso}}}}={frac {4pi A_{text{e}}}{lambda ^{2}}}.}$

So antennas with large effective apertures are considered high-gain antennas (or beam antennas), which have relatively small angular beam widths. As receiving antennas, they are much more sensitive to radio waves coming from a preferred direction compared to waves coming from other directions (which would be considered interference). As transmitting antennas, most of their power is radiated in a particular direction at the expense of other directions. Although antenna gain and effective aperture are functions of direction, when no direction is specified, these are understood to refer to their maximal values, that is, in the direction(s) of the antenna’s intended use (also referred to as the antenna’s main lobe or boresight).

Friis transmission formula[edit]

The fraction of the power delivered to a transmitting antenna that is received by a receiving antenna is proportional to the product of the apertures of both the antennas and inversely proportional to the squared values of the distance between the antennas and the wavelength. This is given by a form of the Friis transmission formula:^[3]

${displaystyle {frac {P_{text{r}}}{P_{text{t}}}}={frac {A_{text{r}}A_{text{t}}}{d^{2}lambda ^{2}}},}$

where

${displaystyle P_{text{t}}}$ is the power fed into the transmitting antenna input terminals,

${displaystyle P_{text{r}}}$ is the power available at receiving antenna output terminals,

${displaystyle A_{text{r}}}$ is the effective area of the receiving antenna,

${displaystyle A_{text{t}}}$ is the effective area of the transmitting antenna,

$d$ is the distance between antennas (the formula is only valid for $d$ large enough to ensure a plane wave front at the receive antenna, sufficiently approximated by ${displaystyle dgtrsim 2a^{2}/lambda }$ , where $a$ is the largest linear dimension of either of the antennas),

$lambda$ is the wavelength of the radio frequency.

Effective length[edit]

Most antenna designs are not defined by a physical area but consist of wires or thin rods; then the effective aperture bears no clear relation to the size or area of the antenna. An alternate measure of antenna response that has a greater relationship to the physical length of such antennas is effective length ${displaystyle l_{text{eff}}}$ measured in metres, which is defined for a receiving antenna as^[4]

${displaystyle l_{text{eff}}=V_{0}/E_{text{s}},}$

where

$V_{0}$ is the open-circuit voltage appearing across the antenna’s terminals,

$E_{s}$ is the electric field strength of the radio signal, in volts per metre, at the antenna.

The longer the effective length, the greater is the voltage appearing at its terminals. However, the actual power implied by that voltage depends on the antenna’s feedpoint impedance, so this cannot be directly related to antenna gain, which is a measure of received power (but does not directly specify voltage or current). For instance, a half-wave dipole has a much longer effective length than a short dipole. However the effective area of the short dipole is almost as great as it is for the half-wave antenna, since (ideally), given an ideal impedance-matching network, it can receive almost as much power from that wave. Note that for a given antenna feedpoint impedance, an antenna’s gain or ${displaystyle A_{text{eff}}}$ increases according to the square of ${displaystyle l_{text{eff}}}$ , so that the effective length for an antenna relative to different wave directions follows the square root of the gain in those directions. But since changing the physical size of an antenna inevitably changes the impedance (often by a great factor), the effective length is not by itself a useful figure of merit for describing an antenna’s peak directivity and is more of theoretical importance.

Derivation of antenna aperture from thermodynamic considerations[edit]

Diagram of antenna A and resistor R in thermal cavities, connected by filter F_ν. If both cavities are at the same temperature $T$ , ${displaystyle P_{text{A}}=P_{text{R}}}$

The aperture of an isotropic antenna, the basis of the definition of gain above, can be derived on the basis of consistency with thermodynamics.^[5]^[6]^[7] Suppose that an ideal isotropic antenna A with a driving-point impedance of R sits within a closed system CA in thermodynamic equilibrium at temperature T. We connect the antenna terminals to a resistor also of resistance R inside a second closed system CR, also at temperature T. In between may be inserted an arbitrary lossless electronic filter F_ν passing only some frequency components.

Each cavity is in thermal equilibrium and thus filled with black-body radiation due to temperature T. The resistor, due to that temperature, will generate Johnson–Nyquist noise with an open-circuit voltage whose mean-squared spectral density is given by

${displaystyle {overline {v_{n}^{2}}}=4k_{text{B}}TR,eta (f),}$

where $eta (f)$ is a quantum-mechanical factor applying to frequency f; at normal temperatures and electronic frequencies ${displaystyle eta (f)=1}$ , but in general is given by

${displaystyle eta (f)={frac {hf/k_{text{B}}T}{e^{hf/k_{text{B}}T}-1}}.}$

The amount of power supplied by an electrical source of impedance R into a matched load (that is, something with an impedance of R, such as the antenna in CA) whose rms open-circuit voltage is v_rms is given by

${displaystyle P={frac {{text{v}}_{text{rms}}^{2}}{4{text{R}}}}.}$

The mean-squared voltage ${displaystyle {overline {v_{n}^{2}}}={text{v}}_{text{rms}}^{2}}$ can be found by integrating the above equation for the spectral density of mean-squared noise voltage over frequencies passed by the filter F_ν. For simplicity, let us just consider F_ν as a narrowband filter of bandwidth B₁ around central frequency f₁, in which case that integral simplifies as follows:

${displaystyle P_{R}={frac {int _{0}^{infty }4k_{text{B}}TR,eta (f),F_{nu }(f),df}{4{text{R}}}}}$

${displaystyle qquad ={frac {4k_{text{B}}TR,eta (f_{1}),B_{1}}{4{text{R}}}}=k_{text{B}}T,eta (f_{1}),B_{1}.}$

This power due to Johnson noise from the resistor is received by the antenna, which radiates it into the closed system CA.

The same antenna, being bathed in black-body radiation of temperature T, receives a spectral radiance (power per unit area per unit frequency per unit solid angle) given by Planck’s law:

${displaystyle {text{P}}_{f,A,Omega }(f)={frac {2hf^{3}}{c^{2}}}{frac {1}{e^{hf/k_{text{B}}T}-1}}={frac {2f^{2}}{c^{2}}},k_{text{B}}T,eta (f),}$

using the notation $eta (f)$ defined above.

However, that radiation is unpolarized, whereas the antenna is only sensitive to one polarization, reducing it by a factor of 2. To find the total power from black-body radiation accepted by the antenna, we must integrate that quantity times the assumed cross-sectional area A_eff of the antenna over all solid angles Ω and over all frequencies f:

${displaystyle P_{A}=int _{0}^{infty }int _{4pi },{frac {P_{f,A,Omega }(f)}{2}}A_{text{eff}}(Omega ,f),F_{nu }(f),dOmega ,df.}$

Since we have assumed an isotropic radiator, A_eff is independent of angle, so the integration over solid angles is trivial, introducing a factor of 4π. And again we can take the simple case of a narrowband electronic filter function F_ν which only passes power of bandwidth B₁ around frequency f₁. The double integral then simplifies to

${displaystyle P_{A}=2pi P_{f,A,Omega }(f)A_{text{eff}},B_{1}={frac {4pi ,k_{text{B}}T,eta (f_{1})}{lambda _{1}^{2}}}A_{text{eff}}B_{1},}$

where ${displaystyle lambda _{1}=c/f_{1}}$ is the free-space wavelength corresponding to the frequency f₁.

Since each system is in thermodynamic equilibrium at the same temperature, we expect no net transfer of power between the cavities. Otherwise one cavity would heat up and the other would cool down in violation of the second law of thermodynamics. Therefore, the power flows in both directions must be equal:

${displaystyle P_{A}=P_{R}.}$

We can then solve for A_eff, the cross-sectional area intercepted by the isotropic antenna:

${displaystyle {frac {4pi ,k_{text{B}}T,eta (f_{1})}{lambda _{1}^{2}}}A_{text{eff}}B_{1}=k_{text{B}}T,eta (f_{1}),B_{1},}$

${displaystyle A_{text{eff}}={frac {lambda _{1}^{2}}{4pi }}.}$

We thus find that for a hypothetical isotropic antenna, thermodynamics demands that the effective cross-section of the receiving antenna to have an area of λ²/4π. This result could be further generalized if we allow the integral over frequency to be more general. Then we find that A_eff for the same antenna must vary with frequency according to that same formula, using λ = c/f. Moreover, the integral over solid angle can be generalized for an antenna that is not isotropic (that is, any real antenna). Since the angle of arriving electromagnetic radiation only enters into A_eff in the above integral, we arrive at the simple but powerful result that the average of the effective cross-section A_eff over all angles at wavelength λ must also be given by

${displaystyle {overline {A_{text{eff}}}}={frac {lambda ^{2}}{4pi }}.}$

Although the above is sufficient proof, we can note that the condition of the antenna’s impedance being R, the same as the resistor, can also be relaxed. In principle, any antenna impedance (that isn’t totally reactive) can be impedance-matched to the resistor R by inserting a suitable (lossless) matching network. Since that network is lossless, the powers P_A and P_R will still flow in opposite directions, even though the voltage and currents seen at the antenna and resistor’s terminals will differ. The spectral density of the power flow in either direction will still be given by ${displaystyle k_{text{B}}T,eta (f)}$ , and in fact this is the very thermal-noise power spectral density associated with one electromagnetic mode, be it in free-space or transmitted electrically. Since there is only a single connection to the resistor, the resistor itself represents a single mode. And an antenna, also having a single electrical connection, couples to one mode of the electromagnetic field according to its average effective cross-section of ${displaystyle lambda _{1}^{2}/(4pi )}$ .

References[edit]

^ ^a ^b ^c ^d IEEE Std 145-2013, IEEE Standard for Definitions of Terms for Antennas. IEEE.
^ Narayan, C. P. (2007). Antennas And Propagation. Technical Publications. p. 51. ISBN 978-81-8431-176-1.
^ Friis, H. T. (May 1946). “A Note on a Simple Transmission Formula”. IRE Proc. 34 (5): 254–256. doi:10.1109/JRPROC.1946.234568. S2CID 51630329.
^ Rudge, Alan W. (1982). The Handbook of Antenna Design. Vol. 1. USA: IET. p. 24. ISBN 0-906048-82-6.
^ Pawsey, J. L.; Bracewell, R. N. (1955). Radio Astronomy. London: Oxford University Press. pp. 23–24.
^ Rohlfs, Kristen; Wilson, T. L. (2013). Tools of Radio Astronomy, 4th Edition. Springer Science and Business Media. pp. 134–135. ISBN 978-3662053942.
^ Condon, J. J.; Ransom, S. M. (2016). “Antenna Fundamentals”. Essential Radio Astronomy course. US National Radio Astronomy Observatory (NRAO) website. Retrieved 22 August 2018.

Notes[edit]

^ Note that antenna gain is also often measured relative to a half-wave dipole (whose gain is 1.64), since the half-wave dipole can be used as an empirical reference antenna. Such antenna gain figures are expressed in decibels using the notation dBd rather than dBi, where the gain is relative to an isotropic antenna.

Источник

Коэффициент использования апертуры[править | править код]

Примечания[править | править код]

См. также[править | править код]

1.2.4.Эффективная площадь антенны

1.2.5. Коэффициент использования площади антенны

Параметры антенн

Параметры антенн

Коэффициент усиления и коэффициент направленного действия

Диаграмма направленности антенны

Ширина луча по уровню половинной мощности

Телесный угол луча

Уровень бокового излучения

Уровень заднего излучения

Эффективная площадь антенны

Полоса частот антенны

Effective area[edit]

Aperture efficiency[edit]

Aperture and gain[edit]

Friis transmission formula[edit]

Effective length[edit]

Derivation of antenna aperture from thermodynamic considerations[edit]

References[edit]

Notes[edit]

Вам также может понравиться

Как найти параметр а по графику функции

Как найти морфала в скайриме

Как найти триггер sql

Добавить комментарий Отменить ответ