1. С помощью рулетки
измерить длину, ширину и высоту аудитории.
2. Рассчитать
площадь пола и кубатуру помещения.
3. Определить
площадь и кубатуру в пересчете на одного
студента (с учетом места, занимаемого
преподавателем), разделив полученные
результаты на число посадочных мест.
1.2 Определение коэффициента аэрации учебной аудитории
1. Осмотреть все
вентиляционные отверстия аудитории.
Проверьте с помощью листа тонкой бумаги,
действуют ли они.
2. Определить общую
площадь всех рабочих вентиляционных
отверстий и фрамуг.
3. Рассчитать
коэффициент аэрации для учебной аудитории
по формуле 1.1:
KA=SOSП
, (1.1)
где 1
– коэффициент аэрации;
Sо
– площадь всех вентиляционных отверстий,
м2;
Sп
– площадь пола, м2.
1.3 Определение эффективности вентиляции учебной аудитории
1. Рассчитать
необходимый вентиляционный объем
воздуха, т.е. объем свежего воздуха,
который необходимо подавать в помещение
на одного человека, чтобы содержание
углекислого газа не превысило
предельно-допустимый уровень (0,1 %),
по формуле 1.2:
V=kp-g∙t
, (1.2)
где V
– вентиляционный
объем, м3;
k
– количество углекислого
воздуха, выделяемое за один астрономический
час, л/ч (подсчитано, что студент при
умственной работе выделяет в среднем
столько углекислого газа, сколько ему
лет);
p
– предельно-допустимое
содержание углекислого газа в воздухе
учебной аудитории (0,1 % или 1 л/м3);
g
– содержание углекислого
газа в атмосферном воздухе (0,03% или 0,3
л/м3);
t
– продолжительность
занятия, ч.
2. Определить
кратность обмена воздуха – число
показывающее, сколько раз в течение 1
часа воздух помещения должен смениться
наружным, чтобы содержание углекислого
газа не превышало предельно-допустимого
уровня. Кратность обмена воздуха
определяется по формуле 1.3:
D=VVСТ
, (1.3)
где D – кратность
обмена воздуха;
V – вентиляционный
объем воздуха, м3;
VСТ – объем воздуха
на одного студента в учебной аудитории,
м3.
Результаты расчетов
сводятся в таблицу 1.1, а также формулируется
вывод о проделанной работе по соответствию
полученных результатов для исследуемой
территории с нормами. В случае отклонения
какого-либо из показателей от нормы
необходимо предложить мероприятия по
устранению недостатков.
Таблица
1.1
– Вентиляционный объем и кратность
обмена воздуха учебной аудитории
|
Аудитория |
Площадь |
Объем |
Коэффициент |
Кратность |
||
|
общая |
на 1 человека |
общий |
на 1 человека |
|||
|
Норма |
Контрольные
вопросы
-
Какие установлены
нормативы для площади и кубатуры учебной
аудитории? -
Что называют
аэрацией? Достоинства и недостатки. -
Какие
санитарно-гигиенические нормы установлены
для аэрации? -
Что называется
вентиляцией? -
Сравните полученные
данные с санитарно-гигиеническими
нормами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Требования к проектированию зданий высших учебных заведений. Размеры и планировка аудиторий.
Стулья для аудиторий в настоящее время большей частью имеют каркас из стальных труб; сиденья и спинки стульев — деревянные. При демонстрации опытов, экспонатов и т.п., когда отдельным студентам приходится часто выходить к демонстрационному столу, рекомендуется разделять ряды, состоящие из спаренных стульев, проходами шириной 50 —55 см, ведущими к демонстрационному столу; возможна также установка поворачиваемых сидении, позволяющих каждому студенту свободно выйти из середины ряда, не мешая соседям (рис. 4). Такие сиденья занимают не больше места, чем стулья с откидными сиденьями (рис. 3), а также чем сиденья на поворотной консоли.
Для одного студента, сидящего в наиболее удобной позе, требуется место площадью 70 х 85 см;
для студента, сидящего в нормальной позе,— 60 х 80= 55 х 75 см.
Площадь, приходящаяся на 1 студента с учетом всех проходов: для наиболее крупных аудиторий и наиболее тесного размещения — 0,6 м2;
для небольших аудиторий, при сидении в нормальной позе — 0,8 —0,95 м2.
При наличии небольших аудиторий высота этажа должна быть ≥ 3,5 м, а при наличии более крупных аудиторий и, в первую очередь аудиторий с круто поднимающимися рядами — значительно больше.
При боковом освещении на самом отдаленном от окна месте, расположенном в верхнем ряду стульев, свет должен попадать на пюпитр под углом 25°. Место для преподавателей, в зависимости от его назначения, оборудуется стационарным демонстрационным столом с встроенными в него кранами водо-и газоснабжения и электрическими розетками или подвижным столом, причем вводы инженерных сетей и выключатели размещаются на передней стенке первого ряда стульев. Высота возвышения над полом первого ряда стульев составляет, в зависимости от назначения аудитории, 20 —60 см. Размеры демонстрационных досок различны; предпочтительны большие доски с раздвижными стеклами с направляющими из стальных трубок, с противовесами на зубчатых цепях.
 |
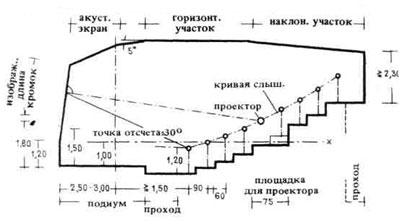 |
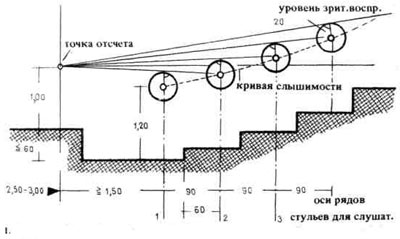
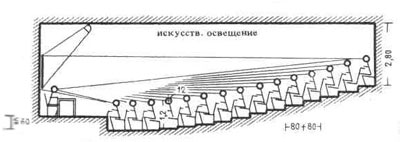
| 1. Графический метод определения кривой слышимости – см.рис.2. | 2. Схематический продольный разрез аудитории; |
 |
 |
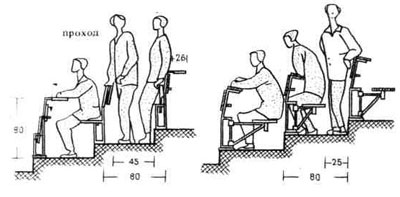
| 3. Места с откидными сидениями и пюпитрами; 4. Места с неподвижными пюпитрами и поворотными сидениями (изобретение Э. Нойферта). |
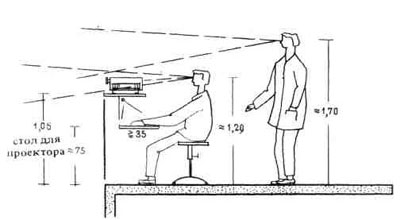
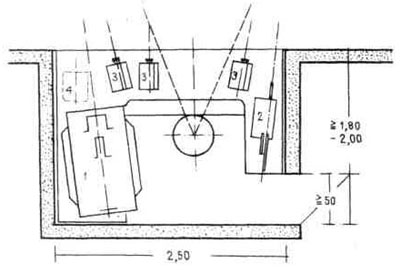
5. Поперечный разрез площадки для установки проекционного аппарата (см. также рис. 6). Уровень зрения в положении сидя приблизительно 1,2, в положении стоя — 1,7. |
 |
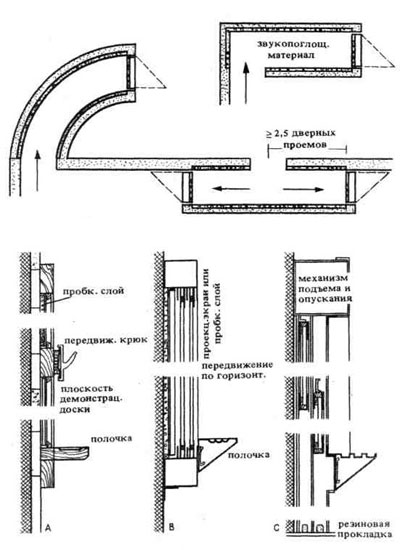 |
| 6. Площадка для установки проекционного аппарата. 1 — большой аппарат; 2 — узкоплёночный аппарат; 3 — малый аппарат для диафильмов; 4 — рабочий аппарат; | 7. Шлюзы для предотвращения проникания в аудиторию света и шума. План.
8. Демонстрационные доски в аудитории. А — неподвижная, Б —передвижная по горизонтали, В — Передвижная по вертикали. |
Требования к школьным зданиям относятся и к высшим учебным заведениям. Современные здания высших учебных заведений состоят из ряда корпусов, расположенных с учетом последующего их расширения. Их группируют вокруг главного корпуса с находящимися в нем главной аудиторией, помещениями ректората, студенческих общественных организаций, основными установками теплоснабжения и энергоснабжения. В институтах в процессе обучения проводятся практические занятия, увязанные с лекциями и демонстрацией опытов в аудиториях. Вход в аудиторию для студентов должен находиться вблизи верхнего ряда (при расположении мест амфитеатром), в очень больших аудиториях он должен быть на середине их высоты. Лекторы должны проходить к кафедре прямо из своих учебных кабинетов.
Иногда входы устраивают из рекреационного помещения, обслуживающего как лекционную аудиторию, так и весь институт (рис. 4 —5).
Во многих случаях в институтском корпусе размещают помещения различных факультетов близких специальностей, для которых помимо общеинститутской аудитории требуются свои аудитории разной вместимости. Общеинститутская аудитория может быть расположена на первом этаже с возможностью устройства повышенной высоты и обычно верхнего света; остальные аудитории следует вписывать в габариты нормальных этажей здания (рис. 5).
В институте оптики Иенского университета высота аудитории повышена за счет использования высоты расположенного над ней помещения (для хранения коллекций института математики), допускающего пониженную высоту. Малая аудитория этого института имеет высоту, равную высоте нормального этажа, в то время, как наибольшая аудитория института прикладной математики возвышается над крышей здания. Входы лекторов во всех случаях рядом с кафедрой; входы для студентов — непосредственно с лестничной клетки к верхним рядам стульев.
Размеры проходов назначаются в зависимости от размеров и формы аудиторий; например, для небольшой аудитории (при открывании створок окон наружу) проходы у окон могут иметь ширину 60 —75 см, внутренние проходы 85 —100 см, а проходы у задней стены аудитории —75 —85 см.
Для более глубоких аудиторий (рис. 5) проходы могут быть шире, для более широких аудиторий рекомендуется устройство второго среднего прохода шириной 75—100 см, который ближе к переднему ряду стульев может сужаться (рис. 7).
Расстояние от первого ряда мест до демонстрационной доски 2,5 —3 м. В наиболее крупных аудиториях ряды кресел должны повышаться в направлении к задней стене (рис. 3); наиболее крутой подъем должен быть в аудиториях с демонстрацией на столе (рис. 4) (например, хирургических клиниках). Чтобы дать возможность студентам наблюдать за операциями на внутренних органах, в США предусматриваются смотровые отверстия в зоне перекрытия, расположенной над операционным столом (рис. 4).
 |
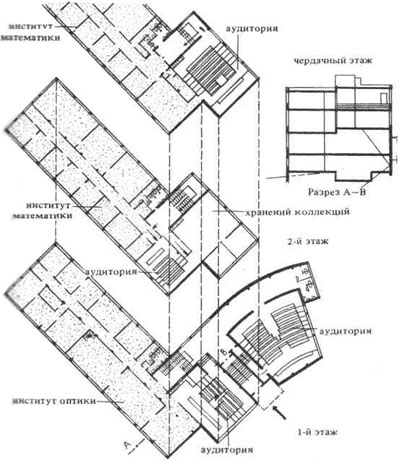 |
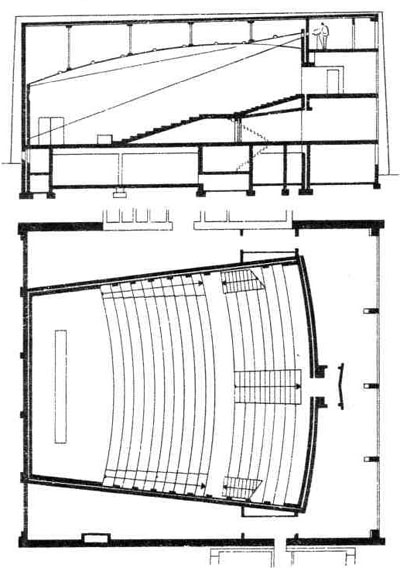
| 1. Стандартная аудитория на 76 мест. План и поперечный разрез. | 4. План корпусов «Аббенаум» Иенского университета (построен в 1929 году) Архитектор Э. Нойферт. |
 |
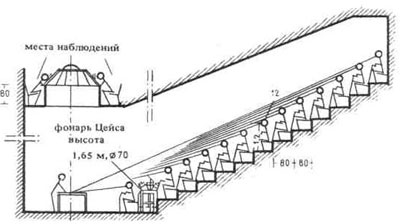 |
| 2. Нормальная форма аудитории; | 3. Аудитория для демонстрации операций (в хирургической клинике). 1 – фонарь Цейса высотой 1,65 м, диаметр 70; 2 – места для студентов, наблюдающих за операцией; |
 |
 |
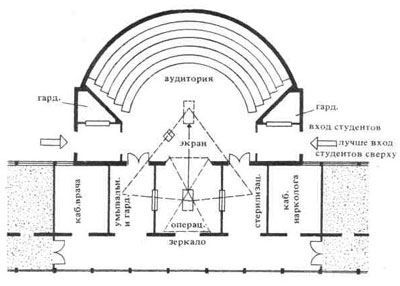
| 5. Аудитория с примыкающей к ней операционной. Предусмотрена возможность проецирования хода операции на экран (матовое стекло). | 6. Физическая аудитория с двойными ограждениями, препятствующими прониканию шума и передаче вибраций. М 1 :400. Высшее техническое училище в Дармштадте. Разрез и план. |
 |
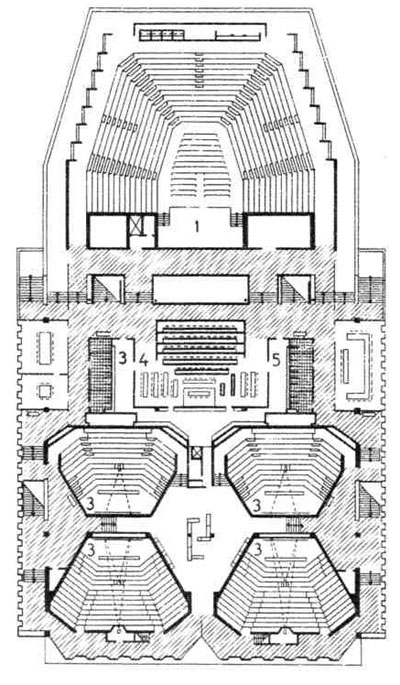 |
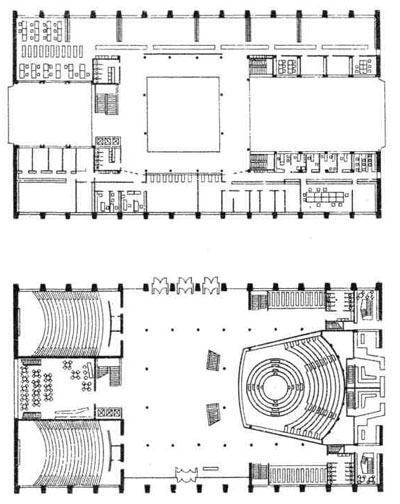
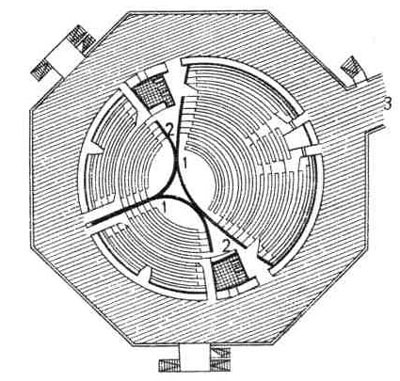
| 7. Аудиторный корпус Фрейбургского университета. Планы типового (вверху) и 1-го (внизу) этажей. Вестибюль и главная аудитория — двусветные. В типовых этажах находятся помещения администрации и помещения для семинарских занятий. Архитектор О. Швейцер; | 10. Аудитория Швейцарского высшего технического училища в г. Цюрих. Архитекторы Штейнер и Гери. 1 — аудитория; 2 — помещение для проектора: 3 —гардеробная. |
 |
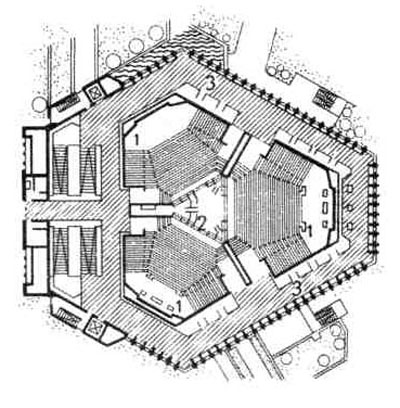 |
| 8. Аудитория Высшего технического училища в г. Дельфт. Архитекторы Брек и Бакема. 1 — главная аудитория; 2 — площадка для проектора; 3 — аудитория; 4 —зал заседаний ученого совета; 5 — гардеробная; | 9. Учебный корпус в г. Дюссельдорф. Архитектор Пфау. 1 — аудитория; 2 — помещение для подготовки к лекциям; 3 — вход; |
Эрнст Нойферт. «Строительное проектирование»/ Ernst Neufert “BAUENTWURFSLEHRE”
УДК 371.62
В.Л. Зудин, доцент Л.Н. Потапов, ассистент
Государственное образовательное учреждение высшего профессионального образования «Ярославский государственный технический университет»
определение конфигурации и площади зоны размещения учащихся в аудитории
Решающую роль в процессе обучения, как известно, играет зрительная информация. Одним из важных аспектов организации учебного процесса с использованием проекционной аппаратуры является требование оптимального размещения учащихся в аудитории. Это требование заключается в том, чтобы учащийся с любого места мог хорошо видеть и слышать то, что преподаватель показывает, пишет или говорит.
Учащиеся размещены в аудитории относительно равномерно по ее площади, каждый из них занимает свое место, ближе или дальше по отношению к преподавателю (доске, экрану и т. п.). Поэтому создать абсолютно одинаковые (тем более оптимальные) условия для каждого из них невозможно. Однако можно говорить об определенной зоне (части площади аудитории), в пределах которой условия видимости будут не ниже некоторых, заранее заданных, нормированных значений. Такую зону можно назвать зоной размещения учащихся.
Поскольку одним из основных источников видеоинформации коллективного пользования являются экранные средства, следует ориентироваться в первую очередь именно на их применение. Одним из очевидных факторов обеспечения наилучших условий наблюдения является расположение плоскости экрана перпендикулярно линии зрения учащихся. Однако очевидно, что для всех зрителей это условие не может быть выполнено и нужно стремиться создать условия, близкие к оптимальным, хотя бы для основной части учащихся. Иначе говоря, следует располагать экран так, чтобы перпендикуляр, проведенный из его центра, проходил через «центр тяжести» зрительской аудитории. Нижняя кромка экрана практически всегда располагается выше среднего уровня глаз наблюдателей (плоскости наблюдения), поэтому оптимальные условия наблюдения могут быть созданы лишь при определенном угле наклоне экрана в сторону зрителей от плоскости стены. По действующим нормам [1] высота плоскости наблюдения над плоскостью пола аудитории должна составлять 1,2 м.
Второе условие, позволяющее определить оптимальную зону размещения учащихся, заключается в том, что любой символ (знак), расположенный
64
на экране, при его наблюдении учащимися в перпендикулярном к экрану направлении, будет виден достаточно четко с некоторого расстояния Ьн. Назовем это расстояние максимальным расстоянием наблюдения.
При изменении позиции наблюдателя от перпендикулярного направления он будет уверенно видеть тот же знак с расстояния несколько меньшего Ьн, поскольку для этого наблюдателя знак как бы сжимается при смене позиции наблюдения (рис. 1). Таким образом, если знак условно вписывается в квадрат со стороной йзн, то при смене позиции (угла наблюдения в) от перпендикулярной экрану угол зрения а уменьшается, а видимый размер знака становится равным Нзн cos р. Чтобы рассмотреть этот знак, наблюдатель должен приблизиться к экрану на расстояние L меньше прежнего. Из построений на рис. 1 легко найти, что расстояние L для угла р связано с максимальным расстоянием наблюдения LK соотношением: L = LK cos р. Эта формула соответствует уравнению окружности с диаметром L , записанному в полярных координатах с полюсом в точке О.
Аналогичный результат можно получить для любого направления и любой плоскости, проходящей через центр знака (горизонтальной, вертикальной, наклонной). Поэтому в конечном итоге мож-
Рис. 1. Влияние угла наблюдения в на расстояние наблюдения L
но считать, что хорошие условия различения знака обеспечиваются, если наблюдатель находится внутри сферы с диаметром Lн, проведенной касательно к плоскости знака в его центре.
Рассматривая строку одинаковых по величине знаков, такую окружность следует изобразить для каждого из них (рис. 2). При этом нетрудно убедиться, что любой знак будет хорошо виден, если наблюдатель находится внутри заштрихованной фигуры. Размеры и положение этой фигуры определяются только крайними знаками строки (точки А и В); радиус R дуг, образующих зону размещения, в рассматриваемом случае равен половине максимального расстояния наблюдения. Расстояние АВ соответствует одному из габаритов изображения (его ширине или высоте). Любой другой знак (например, в точке С) не влияет на размеры и расположение зоны размещения.
Анализируя рис. 2, легко увидеть, что чем больше ширина изображения, тем меньше площадь зоны размещения. То же относится и к случаю использования нескольких (например, двух) экранов: общая площадь зоны размещения будет зависеть от расстояния между крайней левой кромкой изображения на левом экране и крайней правой кромкой изображения на правом экране. При этом ширина каждого из изображений не влияет на размер общей зоны.
Предположим теперь, что знаки заполняют всю плоскость экрана. Чтобы наблюдатель смог уверенно различить любой из них, он должен находиться внутри всех сфер, построенных по рассмотренному выше принципу для каждого знака. Объем, в пределах которого будут обеспечены нормальные условия наблюдения, ограничен пересечением четырех сфер, построенных для знаков, размещенных в углах экрана [2]. Иначе говоря, наблюдатель должен находиться внутри объема, общего для четырех сфер, касающихся углов экрана.
Пересечение полученного выше объема с плоскостью наблюдения определит конфигурацию
А
С В
Рис. 2. Построение зоны размещения для строки знаков
Рис. 3. К определению конфигурации зоны размещения учащихся в аудитории
зоны, в пределах которой будут созданы приемлемые условия наблюдения знаков на экране.
На рис. 3 показаны проекции сфер в вертикальной плоскости (рис. 3а) и проекции объема, получаемого при пересечении четырех сфер с плоскостью наблюдения (рис. 3б). Получаемая при этом пересечении конфигурация зоны размещения образована радиусами R1 и R2, проведенными из точек пересечения линий, соответствующих высоте Н экрана на расстоянии Lн / 2 от него, с линиями, соответствующими ширине В экрана.
При изменении угла 0 наклона экрана к вертикальной плоскости будет меняться размещение сфер по отношению к плоскости наблюдения, положение «центра тяжести» аудитории (параметр С) и величина площади зоны размещения. Из анализа геометрических построений (рис. 3а) следует:
Я =. –
h——– БІП 0 + Н 00Б 0
2
h – БІП 0 2
где к — расстояние от плоскости наблюдения до нижней кромки экрана.
2
2
Для вычисления площади зоны размещения удобнее воспользоваться более подробным чертежом, приведенным на рис. 4. Половина площади зоны размещения представляет собой фигуру, ограниченную дугами AG, GD и осью AD. Для ее определения можно вычислить интеграл фигуры TAGDN и вычесть из него площадь прямоугольника ADNT.
Площадь фигуры TAGDN удобно представить в виде суммы площадей, являющихся частями двух окружностей и вычисляемых как интегралы. Одна из этих частей представляет собой фигуру AGQ с центром в точке О1 (ось 71) и радиусом другая — фигуру GDQ с центром в точке О2 (ось Y2) и радиусом R2. Расстояние между осями составляет С1 = Н sin 0.
Из построений на рис. 4 нетрудно определить пределы интегрирования для каждого интеграла. Так, для площади AGQ нижний а1 предел находится из треугольника О1АТ, а и верхний b1 предел — из совместного решения треугольников 02GM и 01GM относительно отрезка GM:
Аналогично для интеграла S2
S2 = –
-arcsin
R2
fCx н Ь2 Л
R
Vr2 – (C,
н—- arccos 2
x2R У
4^R
Вычитаемая из суммы интегралов 51 и 52 площадь прямоугольника АБЫТ составляет
5 = | ( – С1 + Ъ2).
Таким образом, окончательное значение площади 5 зоны размещения может быть определено по формуле
S = 2(S, н S2 – S3) = R,2
arccos
v
B
2R1
b1
н arcsin—
R
1
a =-/R,2 – —
b1 =
R22 – R2 – CL2
2C
arccos
B
2R
– – arcsin
Ci н b, R
R,2 – b2
Для второго интеграла, определяемого площадью фигуры GDQ, пределы интегрирования составят:
-(C, + bi^r2 – (bi+C,)2 -Bу.
4R2 – B2
&2 — ^1 + b^j b2 — Вычисление интеграла S дает:
■V R2 – b2
R2
S, = —arcsin
12
R2
arccos
B
4R22 – B2 )- BCL.
Анализ показывает, что значение S, полученное по последней формуле, истинно лишь при соблюдении условия R2 – R1 < H sin 0. В противном случае следует пользоваться соотношением, получаемым при R2 = 0:
v2Ri у
н B{4 R,2 – bi2
S„ = 2R arccos
B
2R,
1
4
~~ 14R2 – B2.
Необходимость использования различных формул объясняется изменением конфигурации зоны размещения при разных углах наклона плоскости экрана. Если при значительных углах конфигурация зоны определяется обоими радиусами, то при малых углах верхние сферы не пересекают плоскость наблюдения и конфигурация зоны зависит только от одного радиуса. В первом случае вычисляется площадь 5, во втором — 5о.
На рис. 5 приведены графики изменения радиусов R1, R2 (по левой оси ординат) и площади 5 (по правой оси) при изменении угла 0 наклона экрана к вертикальной плоскости от 0 до 30° для L = 10 м, Н = 1,5 м, В = 2 м, к = O0)5Lн.
я1г Я2
Б, м2 70
Угол наклона экрана
65
60
55
50
45
40
-Я1 ——-Я2 ——-Б
Рис. 5. Результаты расчета радиусов и площади зоны размещения (пример)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Нетрудно видеть, что в области равенства значений Я1 и Я2 изменение площади 5 весьма невелико и примерно соответствует максимальному значению. Поэтому целесообразно выбирать такие углы наклона экрана, при которых наблюдается примерное равенство расчетных значений радиусов Я 1 и Я2. Следует отметить, что прямое приравнивание значений радиусов по приведенным выше формулам дает тривиальное решение 0 = 90° и не имеет практического смысла, поэтому должен быть использован другой аппарат вычисления.
Список литературы
1. Строительные нормы и правила СНиП 2.08.02-89. Общественные здания и сооружения.
2. Техника систем индикации. — М.: Мир, 1970. — 520 с.
УДК 378.146
Ж.В. Нечеухина, ст. преподаватель
Государственное образовательного учреждение высшего профессионального образования «Курганский государственный университет»
организационно-педагогическое обеспечение оценочных средств итоговой аттестации педагога профессионального обучения
Одной из приоритетных задач при реализации государственных образовательных стандартов высшего профессионального образования (ГОС ВПО) является оценка уровня профессиональной подготовки выпускников вузов, которая, как правило, заключается в оптимизации и совершенствовании оценочных средств, методов и технологий, применяемых в ходе итоговой аттестации.
Вопросы теории, практики и технологии создания оценочных средств итоговой аттестации выпускников вузов на соответствие требованиям ГОС ВПО рассмотрены в работах таких известных ученых, как И.Н. Бородулин, Б.К. Коломиец, А.И. Су-бетто, Н.И. Максимов, Ю.Г. Татур, В.Г. Казанович, Г.П. Савельева, В.М. Соколов и др. Проблеме оценки конечных результатов образования выпускников вузов в рамках компетентностного подхода посвящены исследования В.И. Байденко, И.А. Зимней, А.В. Хуторского, О.В. Никифорова и др.
Различные подходы к оценке подготовленности выпускников, представленные в трудах Б.К. Коло-мийца, Н.А. Нещерета, С.И. Тарасовой, Т.Н. Беспаловой, Л.И. Анищевой, Н.А. Гришановой, Т.В. Лопуховой, Г.П. Кабанова, В.В. Бажутина, Е.Ю. Игнатьева и др., характеризуются отсутствием целостной оценочно-критериальной системы. Традиционные
показатели и критерии, по которым оценивают качество подготовки выпускников, зачастую основаны на интуиции и личном мнении оценивающих и являются субъективными.
Изучение опыта итоговой аттестации (дипло-мирования) будущих педагогов профессионального обучения [1] показало, что применяемые в практической деятельности вузов оценочные средства не позволяют в полной мере определить степень подготовленности выпускников на соответствие требованиям ГОС ВПО [2] из-за отсутствия необходимых для этого условий, например, таких как незнание и непонимание участниками итоговой аттестации требований стандарта, отсутствие единых подходов к оценке подготовленности выпускников и др. Неопределенность в выборе квалификационных требований, выносимых на итоговую аттестацию, позволила вузам стихийно создавать разнообразные средства оценки, порой неадекватные требованиям стандарта. В рамках существующих итоговых испытаний традиционно оцениваются отдельные составляющие подготовки выпускников (психолого-педагогическая и отраслевая), что противоречит целостному интегративному характеру деятельности педагога профессионального обучения.
67
