Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
|
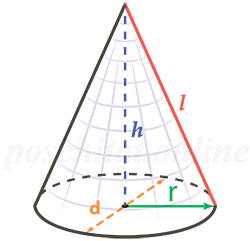
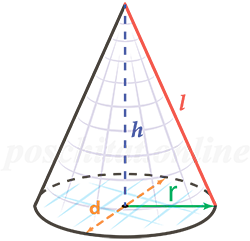
Рис. (1). Конус |
Площадь боковой поверхности конуса вычисляется по формуле: где (R) — радиус конуса, (l) — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) = Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3 |
Площадью боковой поверхности конуса является площадь её развёртки.
Развёрткой боковой поверхности конуса является круговой сектор.
|
Рис. (2). Развёртка конуса |
α
— градусная мера центрального угла. Радиус этого сектора — образующая конуса (AK = KB = l)
|
Источники:
Рис. 1. Конус. © Якласс
Рис. 2. Развёртка конуса. © Якласс
Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
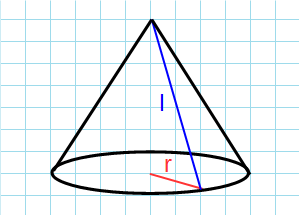
Формула боковой поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Боковая поверхность через радиус и высоту
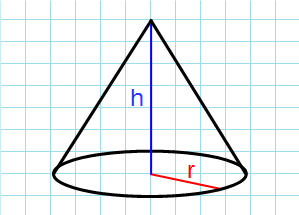
Формула боковой поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π – константа равная (3.14); l – образующая конуса; r – радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой – сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
§ 18. Конус
18.1.Определение конуса и его элементов
Определение. Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащей его катет, называется прямым круговым конусом (рис. 165, 166).
Отрезок оси вращения, заключённый внутри конуса, называется осью конуса.
Круг, образованный при вращении второго катета, называется основанием конуса. Длина этого катета называется радиусом основания конуса или, короче, радиусом конуса. Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса. На рисунках 165, б и 166 вершиной конуса является точка Р.
Высотой конуса называется отрезок, проведённый из вершины конуса перпендикулярно его основанию. Длину этого перпендикуляра также называют высотой конуса. Высота конуса имеет своим основанием центр круга — основания конуса — и совпадает с осью конуса.
Отрезки, соединяющие вершину конуса с точками окружности его основания, называются образующими конуса. Все образующие конуса равны между собой (почему?).
Как и в случае с цилиндром, можно рассматривать конус в более широком, чем у нас, понимании, когда в основании конуса может быть, например, эллипс (эллиптический конус), парабола (параболический конус). Мы будем изучать только определённый выше прямой круговой конус (конус вращения), поэтому слова «прямой круговой» мы будем опускать.

Рис. 165

Рис. 166

Рис. 167
Поверхность, полученная при вращении гипотенузы, называется боковой поверхностью конуса, а её площадь — площадью боковой поверхности конуса и обозначается Sбок. Боковая поверхность конуса является объединением всех его образующих.
Объединение боковой поверхности конуса и его основания называется полной поверхностью конуса, а её площадь называется площадью полной поверхности конуса или, короче, площадью поверхности конуса и обозначается Sкон. Из этого определения следует, что
Sкон = Sбок + Sосн.
Если вокруг данной прямой — оси — вращать пересекающую её прямую, то при этом вращении образуется поверхность, которую называют круговой конической поверхностью или конической поверхностью вращения. Уравнение  +
+  –
–  = 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
= 0 задаёт коническую поверхность вращения с осью вращения Oz (рис. 167). Из этого уравнения следует, что коническая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» — в конце этой книги.)
18.2. Сечения конуса
Определение. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением конуса.

Рис. 168

Рис. 169

Рис. 170
Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники. На рисунке 168 осевым сечением конуса является треугольник ABP (АР = ВР). Угол АPВ называют углом при вершине осевого сечения конуса.
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением.

Рис. 171
 Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками.
О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги. 
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60°; б) в 90°. Найти площадь сечения.

Решение. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60°, значит, △ AOB — правильный и АВ = R.
Рис. 172
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S△ ABP =  АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =
АВ•РC. Имеем: ОР = R (по условию); в △ AOB: ОС =  ; в △ ОСР: CP =
; в △ ОСР: CP =  =
=  .
.
Тогда S△ ABP =  АВ•РС =
АВ•РС =  .
.
Ответ: а)  .
.
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Рис. 173
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса

Рис. 174
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р.

Рис. 175

Рис. 176
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a), то получим развёртку поверхности конуса (рис. 176, б), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α =  .
.
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
Sбок =  α•l2,(1)
α•l2,(1)
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α =  , получаем:
, получаем:
Sбок = πRl.(2)
Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
Sкон = πRl + πR2.(3)

Следствие. Пусть конус образован вращением прямоугольного треугольника ABC вокруг катета АС (рис. 177). Тогда Sбок = π•BC•АВ. Если D — середина отрезка АВ, то AB = 2AD, поэтому
Sбок = 2 π ВС•AD.(4)

Рис. 177
Проведём DE ⟂ АB (E ∈ l = AС). Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А) имеем
 =
=  ⇒ BC•AD = DE•АС.(5)
⇒ BC•AD = DE•АС.(5)
Тогда соотношение (4) принимает вид
Sбок = (2π•DE)•AC,(6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса


Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Рис. 178
Доказательство. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α, параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β, α || β, то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O1 = α ∩ РО. Обозначим этот круг F1.
Рассмотрим гомотетию  с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия  отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии
отображает основание F конуса на его параллельное сечение — круг F1, при этом центр О основания отображается на центр О1 круга F1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии  точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
точка X отображается на точку X1 = РX ∩ α. Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:
 =
=  = k,(*)
= k,(*)
где k — коэффициент гомотетии  , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
, т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.
А поскольку гомотетия является подобием, то круг F1, являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO1 : РО, где РO1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
Sсечен : Sоснов = k2 =  : PO2.
: PO2.
Теорема доказана. ▼
18.7.Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
—строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
—соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
—выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
—прямоугольный треугольник (см. рис. 179);
—правильный треугольник (см. рис. 180);
—квадрат (см. рис. 181);
—правильный шестиугольник (см. рис. 182).

Рис. 179

Рис. 180

Рис. 181

Рис. 182
Определение. Пирамида называется описанной около конуса, если у них вершина общая, а основание пирамиды описано около основания конуса. В этом случае конус называют вписанным в пирамиду (рис. 183).

Рис. 183

Рис. 184
ЗАДАЧА (3.080). В равносторонний конус вписана правильная пирамида. Найти отношение площадей боковых поверхностей пирамиды и конуса, если пирамида: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай а). Пусть R — радиус основания равностороннего конуса, РАВС — правильная пирамида, вписанная в этот конус (рис. 184); △ DPE — осевое сечение конуса, CF — медиана △ АBС. Тогда в △ АВС (правильный): АВ = R , OF =
, OF =  R; в △ DPE (правильный): ОР =
R; в △ DPE (правильный): ОР =  = R
= R ; в △ ОРF (∠ FOP = 90°):
; в △ ОРF (∠ FOP = 90°):
PF =  =
=  .
.
Так как CF — медиана △ АВС, то PF — высота равнобедренного треугольника АВР. Поэтому
S△ ABP =  AB•PF =
AB•PF =  R
R •
•  =
=  .
.
Обозначим: S1 — площадь боковой поверхности пирамиды, S2 — площадь боковой поверхности конуса. Тогда
S1 = 3S△ ABP =  ,
,
S
2 = πR•PA = πR•2R = 2πR2.
Следовательно,
S1 : S2 =  : 2πR2 =
: 2πR2 =  .
.
Ответ: а)  .
.


 Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =
Во многих пособиях по геометрии за площадь боковой поверхности конуса принимают предел последовательности боковых поверхностей правильных вписанных в конус (или описанных около конуса) п-угольных пирамид при n → +∞. Действительно, Sбок. пов. пирам =  •a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl.
•a•Poсн. пирам, где Рoсн. пирам — периметр основания пирамиды, а — апофема боковой грани. Для правильных описанных около конуса пирамид апофема a — постоянная величина, равная образующей l конуса, а предел последовательности периметров правильных многоугольников, описанных около окружности радиуса R основания конуса, равен 2πR — длине этой окружности. Таким образом, мы вновь получаем: Sбок = πRl. 
18.8. Усечённый конус

Рис. 185
Пусть дан конус с вершиной Р. Проведём плоскость α, параллельную плоскости основания конуса и пересекающую этот конус (рис. 185). Эта плоскость пересекает данный конус по кругу и разбивает его на два тела: одно из них является конусом, а другое (расположенное между плоскостью основания данного конуса и секущей плоскостью) называют усечённым конусом. Таким образом, усечённый конус представляет собой часть полного конуса, заключённую между его основанием и параллельной ему плоскостью. Основание данного конуса и круг, полученный в сечении этого конуса плоскостью α, называются соответственно нижним и верхним основаниями усечённого конуса. Высотой усечённого конуса называется перпендикуляр, проведённый из какой-либо точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённого конуса. (Часто за высоту усечённого конуса принимают отрезок, соединяющий центры его оснований.)

Рис. 186

Рис. 187
Часть боковой поверхности данного конуса, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса, а отрезки образующих конуса, заключённые между основаниями усечённого конуса, называются образующими усечённого конуса. Так как все образующие данного конуса равны и равны все образующие отсечённого конуса, то равны все образующие усечённого конуса.
Построение изображения усечённого конуса следует начинать с изображения того конуса, из которого получился усечённый конус (рис. 186).
На рисунке 187 показана развёртка усечённого конуса.
Из теоремы 28 следует, что основания усечённого конуса — подобные круги.
Определения усечённой пирамиды, вписанной в усечённый конус и описанной около него, аналогичны определениям пирамиды, вписанной в конус и описанной около него.
Заметим, что построение изображений усечённой пирамиды, вписанной в усечённый конус и описанной около него, следует начинать с изображений того конуса или той пирамиды, из которых получены соответственно усечённые конус и пирамида.
Полной поверхностью усечённого конуса называется объединение боковой поверхности этого конуса и двух его оснований. Иногда полную поверхность усечённого конуса называют его поверхностью, а её площадь — площадью поверхности усечённого конуса. Эта площадь равна сумме площадей боковой поверхности и оснований усечённого конуса.
Усечённый конус может быть образован также вращением прямоугольной трапеции вокруг боковой стороны трапеции, перпендикулярной её основанию.

Рис. 188
На рисунке 188 изображён усечённый конус, образованный вращением прямоугольной трапеции ABCD вокруг стороны CD. При этом боковая поверхность усечённого конуса образована вращением боковой стороны АВ, а основания его — вращением оснований AD и ВС трапеции.
18.9. Поверхность усечённого конуса
Выразим площадь Sбок боковой поверхности усечённого конуса через длину l его образующей и радиусы R и r оснований (R > r).

Рис. 189
Пусть точка Р — вершина конуса, из которого получен усечённый конус; точки О, O1 — центры оснований усечённого конуса; AA1 = l — одна из образующих усечённого конуса (рис. 189).
Используя формулу (2) п. 18.5, получаем
Sбок = πR•PA – πr•РA1 =
= πR(РA1 + А1A) – πr•PA1 =
= πR•A1A + π(R – r)•PA1.
Учитывая, что A1A = l, имеем
Sбок = πRl + π(R – r)PA1.(7)
Выразим PA1 через l, R и r. Так как O1A1 || OA и OO1 — высота усечённого конуса, то прямоугольные треугольники POA и PO1A1 подобны. Поэтому АО : А1O1 = PA : PA1 или
R : r = (PA1 + A1A) : PA1, откуда
R•PA1 = r(PA1 + l) ⇒ (R – r)PA1 = rl ⇒ PA1 =  .
.
Подставив это значение РА1 в (7), получаем
Sбок = π(R + r)l.(8)
Таким образом, доказана следующая теорема.

Теорема 29. Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую. ▼
Площадь полной поверхности усечённого конуса находится по формуле:
Sполн = π•(R + r)•l + π•R2 + π•r2.

Следствие. Пусть усечённый конус образован вращением прямоугольной трапеции ABCD вокруг её высоты AD (рис. 190). Тогда Sбок = π (АВ + DC)•ВС. Если KЕ — средняя линия трапеции, то АВ + DC = 2KE, поэтому
Sбок = 2π•KE•BC.(9)

Рис. 190
Проведём EF ⟂ ВС. Из подобия прямоугольных треугольников ВСН и EFK имеем
BC : EF = BH : KE ⇒ ⇒ KE•BC = EF•BH.(10)
Тогда равенство (9) принимает вид
Sбок = (2π•EF)•ВH,(11)

т. е. боковая поверхность усечённого конуса равна произведению его высоты на длину окружности, радиус которой равен серединному перпендикуляру, проведённому из точки оси конуса к его образующей.
18.10. Объёмы конуса и усечённого конуса
Найдём объём конуса, высота которого равна h и радиус основания — R. Для этого расположим этот конус и правильную четырёхугольную пирамиду, высота которой равна h и сторона основания — R, так, чтобы их основания находились на одной и той же плоскости α, а вершины — также в одной и той же плоскости β, параллельной плоскости α и удалённой от неё на расстояние h (рис. 191).

Рис. 191
Каждая плоскость, параллельная данным плоскостям и пересекающая конус, пересекает также пирамиду; причём площади сечений, образованных при пересечении обоих тел, относятся к площадям оснований этих тел, как квадраты их расстояний от вершин. А так как секущие плоскости для пирамиды и для конуса равноудалены от их вершин, то  =
=  . Тогда
. Тогда  =
=  =
=  = π, значит, для объёмов этих тел выполняется:
= π, значит, для объёмов этих тел выполняется:
Vкон : Vпир = π : 1 или Vкон :  R2•h = π : 1, откуда
R2•h = π : 1, откуда
Vкон =  πR2 •h.
πR2 •h.

Рис. 192
Самостоятельно рассмотрите усечённые конус и пирамиду, расположенные в соответствии с условиями принципа Кавальери. Тогда вы получите формулу вычисления объёма усечённого конуса:
Vус. кон =  π•h•(R2 + r•R + r2).
π•h•(R2 + r•R + r2).
Эту же формулу вы можете вывести, если используете идею подобия так же, как это сделано в случае с выводом формулы площади боковой поверхности усечённого конуса.

Используя принцип Кавальери, докажите, что объём каждого из тел, на которые конус разбивается его сечением плоскостью, проходящей через вершину (рис. 192), может быть вычислен по формуле V =  •h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
•h•Scегм, где h — длина высоты конуса, а Sceгм — площадь соответствующего сегмента основания конуса.
