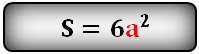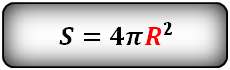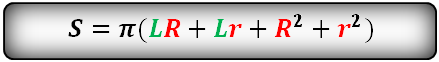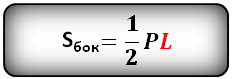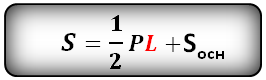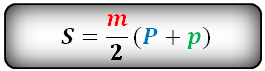Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба
a – сторона куба
Формула площади поверхности куба,(S):
2. Найти площадь поверхности прямоугольного параллелепипеда
a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
3. Найти площадь поверхности шара, сферы
R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
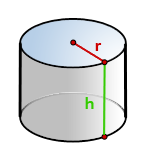
4. Найти площадь боковой и полной поверхности цилиндра
r – радиус основания
h – высота цилиндра
π ≈ 3.14
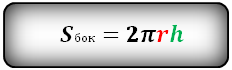
Формула площади боковой поверхности цилиндра, (Sбок):
Формула площади всей поверхности цилиндра, (S):
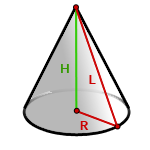
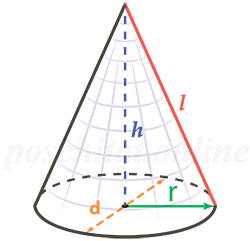
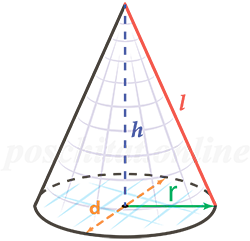
5. Площадь поверхности прямого, кругового конуса
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
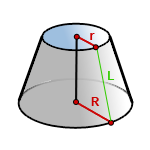
6. Формулы площади поверхности усеченного конуса
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):
Формула площади полной поверхности усеченного конуса, (S):
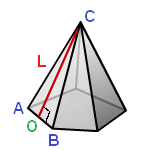
7. Площадь поверхности правильной пирамиды через апофему
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
Формула площади полной поверхности правильной пирамиды (S):
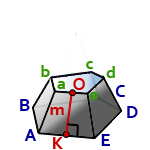
8. Площадь боковой поверхности правильной усеченной пирамиды
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
9. Площадь поверхности шарового сегмента
R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):
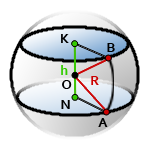
10. Площадь поверхности шарового слоя
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):
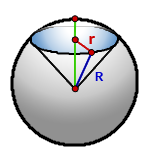
11. Площадь поверхности шарового сектора
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
Напомним,
что конус – это тело, полученное при вращении прямоугольного
треугольника вокруг прямой, проходящей через один из его катетов.
Назовём
элементы конуса.
Осью
конуса называется прямая вращения.
Основание конуса
– круг радиуса ,
который равен катету треугольника вращения.
Радиус
конуса –
это радиус его основания.
Вершина
конуса – неподвижная вершина треугольника вращения.
Образующая
конуса –
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.
Высота конуса
–
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.
В
конусе радиус основания ,
высота и
образующая связаны
следующим соотношением:
.
Сечение
конуса плоскостью, проходящей через его вершину, представляет собой
равнобедренный треугольник, у которого боковые стороны являются образующими
конуса.
Осевым
сечением конуса называется сечение конуса плоскостью,
проходящей через его ось.
Осевое
сечение конуса – равнобедренный треугольник, боковые стороны
которого – образующие, а основание – диаметр основания конуса.
Боковую
поверхность конуса, как и боковую поверхность цилиндра,
можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой
боковой поверхности конуса является круговой сектор.
Обратите
внимание, радиус сектора равен образующей конуса,
а длина дуги сектора равна длине окружности основания конуса.
Площадь
боковой поверхности конуса можно вычислить по следующим
формулам:
,
,
,
где
–
длина окружности основания, –
радиус основания, –
образующая.
Площадь
полной поверхности конуса равна сумме площади боковой поверхности конуса и
площади его основания.
Тогда
площадь полной поверхности конуса можно вычислить по формуле^
,
где
–
радиус основания конуса, –
его образующая.
Объём конуса
равен одной третьей произведения площади основания на высоту.
Тогда
его можно вычислить по формуле:
,
где
–
радиус основания конуса, –
его высота.
Плоскость,
параллельная плоскости основания конуса, пересекает конус по кругу, а боковую
поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает
конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая
(нижняя) называется усечённым конусом.
Усечённым
конусом называется часть конуса, ограниченная его основанием
и сечением, параллельным плоскости основания. Усечённый конус имеет ось,
высоту ,
радиусы оснований и
,
образующую .
Осевое сечение усечённого конуса – равнобедренная трапеция.
Площадь
боковой поверхности усечённого конуса и объём усечённого конуса равен разности
площадей боковых поверхностей и объёмов полного конуса и отсечённого.
,
Площадь
боковой поверхности усечённого конуса можно найти по следующим
формулам:
,
Объём
усечённого конуса можно вычислить по следующим формулам:
,
где
и
–
площади оснований, –
высота усечённого конуса;
или
,
где
–
высота усечённого конуса, и
–
радиусы верхнего и нижнего оснований.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. Радиус основания конуса равен см,
высота конуса равна см.
Найдите площадь боковой поверхности и объём конуса.
Решение.
Задача
вторая. В конус вписана правильная треугольная пирамида с
площадью основания см2
и углом наклона бокового ребра к основанию, равным .
Найдите объём и площадь полной поверхности конуса.
Решение.
Задача
третья. В равносторонний конус с радиусом основания, равным см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение .
Решение.
Задача
четвёртая. Длины радиусов оснований и образующей усечённого
конуса равны соответственно см,
см
и см.
Вычислите его высоту.
Решение.
S=2R*h, где S — площадь сечения, R – радиус окружности основания, заданный условиями задачи, а h — высота цилиндра, также заданная условиями задачи. Если сечение перпендикулярно основаниям, но при этом не проходит через ось вращения, прямоугольника не будет равняться диаметру окружности.
Как найти площадь осевого сечения цилиндра если известна высота и радиус?
Площадь осевого сечения цилиндра равна произведению его высоты h на удвоенный радиус R (т.
Какой фигурой является осевое сечение цилиндра как находится площадь осевого сечения цилиндра если известны радиус и высота цилиндра?
Объяснение: Осевое сечение цилиндра — прямоугольник. Оно выполняется плоскостью, которая проходит по оси цилиндра. Площадь осевого сечения находится как площадь прямоугольника, одна сторона которого равна высоте цилиндра , а другая — диаметру (удвоенному радиусу) цилиндра.
Что такое площадь осевого сечения цилиндра?
Площадь осевого сечения цилиндра равна произведению высоты цилиндра на его диаметр.
Как найти высоту цилиндра если известен радиус?
Рассмотрим формулу, с помощью которой можно найти высоту: V=πR^2*H, где R — радиус основания цилиндра, H — искомая высота. Также высоту можно определить, исходя из диаметра и площади цилиндра.
Как найти площадь бокового сечения цилиндра?
Площадь боковой поверхности цилиндра равна произведению высоты цилиндра на длину окружности основания.
Как найти площадь боковой поверхности цилиндра Если известна площадь осевого сечения?
Площадь боковой поверхности цилиндра равна произведению длины окружности на высоту цилиндра h: .
Как называется Цилиндр осевое сечение которого квадрат?
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Что представляет собой сечение цилиндра Если секущая плоскость проходит через ось цилиндра?
Пусть секущая плоскость проходит через ось цилиндра. Такое сечение называют осевым. Оно представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Если секущая плоскость перпендикулярна оси цилиндра, то сечение является кругом.
Как найти диагональ осевого сечения цилиндра?
По теореме Пифагора (c2 = a2 + b2) найдите диагональ осевого сечения:D. = √〖(4R〗^2+H^2), где D – диагональ осевого сечения цилиндра, R – радиус основания, H – высота цилиндра.
Как найти объем цилиндра через диаметр и высоту?
Объём цилиндра формула
Или диаметр. S = Пи х (D / 2)² х h.