Как найти площадь боковой грани усеченной пирамиды

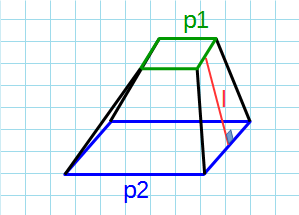
Формула площади боковой поверхности усеченной пирамиды через периметры и апофему:

p1 – периметр верхнего основания; p2 – периметр нижнего основания; l – апофема усеченной пирамиды.

Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.

Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:

Таким же образом находим периметр меньшего основания:

Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:

Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.

Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.

Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.

Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:


Теперь используем найденные значения для расчета площади боковой поверхности.

§ 1  Усеченная пирамида в повседневности

На уроке мы рассмотрим усеченную пирамиду, а именно правильную усеченную пирамиду. Разберем свойства усеченной пирамиды и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.

Если посмотреть на купюру 1 доллар, то можно увидеть на ней пирамиду, разделенную на две части, таким же образом как мы поступили сейчас с вами, проводя сечение параллельное основанию пирамиды. Загадка, не иначе. Для чего и зачем это сделано. Догадок много. И в данном случае прослеживается желание наделить бумагу магической силой пирамид, еще и усилив ее масонским символом в вершине. Как повествует одна мудрая пословица «если бы не строители пирамид, кто бы знал имена фараонов». Попробуйте найти еще примеры усеченной пирамиды, и вы будете удивлены своим находкам.

§ 2  Площадь боковой поверхности правильной усеченной пирамиды

Прежде чем говорить о свойствах правильной усеченной пирамиды напомним ее определение. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.

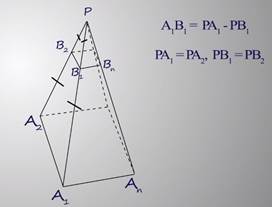
Думаю, Вы заметили, одно из утверждений требует доказательства. Боковые грани правильной усеченной пирамиды равнобедренные трапеции. Докажем этот факт. Рассмотрим боковую грань пирамиды – равнобедренный треугольник РА1А2 с боковыми сторонами РА1 и РА2. Отрезок В1В2 в этом треугольнике параллелен основанию, а значит, мы можем рассматривать два подобных треугольника А1А2 и РВ1В2, оба они равнобедренные. Выразим сторону А1В1, она равна разности РА1 и РВ1, а так как РА1=РА2, и РВ1=РВ2, то разность примет вид: РА2 – РВ2, а это есть отрезок А2В2. Приравняем начало и конец данного рассуждения и получим А1В1=А2В2, что и требовалось доказать! Боковые грани правильной усеченной пирамиды являются равнобедренными трапециями.

Раз мы доказали, что боковые грани правильной усеченной пирамиды равнобедренные трапеции, то мы сможем с легкостью вывести формулу для вычисления площади боковой поверхности такого многогранника. Площадь одной грани находится как полусумма ребер оснований умноженная на апофему. Просуммируем все грани и вынесем за скобки общий множитель ½ апофемы. В скобках получится сумма ребер верхнего основания и сумма ребер нижнего основания, что является их периметрами. Множитель ½ из суммы периметров сделает полусумму периметров и формула примет готовый вид. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Мы с вами справились с доказательствами утверждений и выводом очень важной формулы применяемой при решении задач.

Список использованной литературы:

1. Геометрия. 10 – 11 классы : учебник для общеобразоват. учреждений : базовый и профил. уровни / [ Л. С. Атанасян, В. Ф. Бутузов, С.Б. Кадомцев и др.]. – 22-е изд. – М. : Просвещение, 2013. – 255 с. : ил. – (МГУ – в школе)
2. Учебно – методическое пособие в помощь школьному учителю. Составитель Яровенко В.А. Поурочные разработки по геометрии к учебному комплекту Л. С. Атанасяна и др. ( М. : Просвещение) 10 класс
3. Рабинович Е. М. Задачи и упражнения на готовых чертежах. 10 – 11 классы. Геометрия. – М. : Илекса , 2006 . – 80 с.
4. М. Я Выгодский Справочник по элементарной математике М.: АСТ Астрель , 2006. – 509с.
5. Аванта+. Энциклопедия для детей. Том 11. Математика 2-е изд., перераб.— М.: Мир энциклопедий Аванта+: Астрель 2007. — 621 с. Ред. коллегия: М. Аксёнова, В. Володин, М.Самсонов.

Использованные изображения:

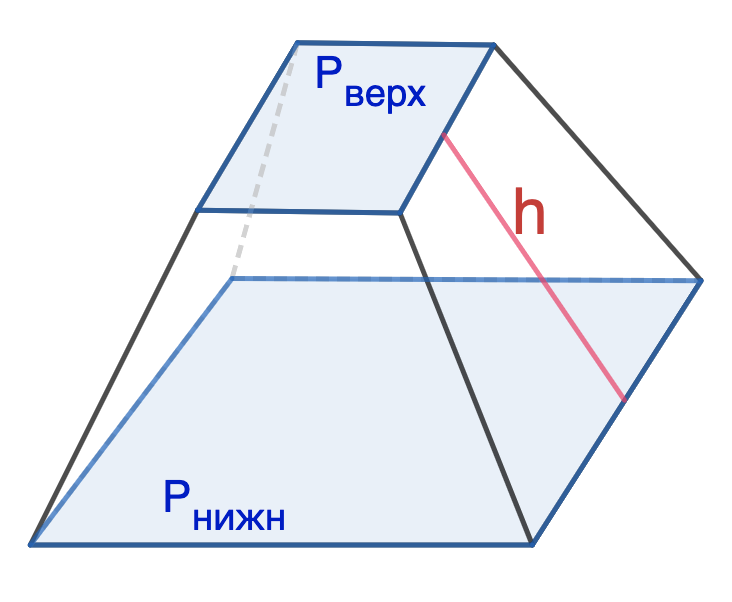
Периметр верхнего основания (P1)

Периметр нижнего основания (P2)

Апофема (h)