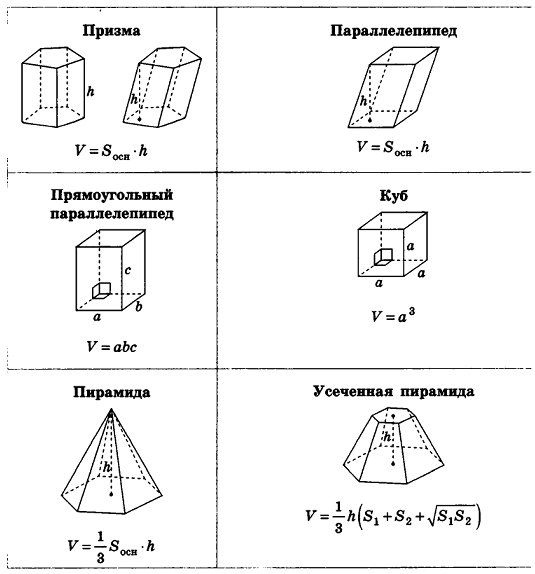
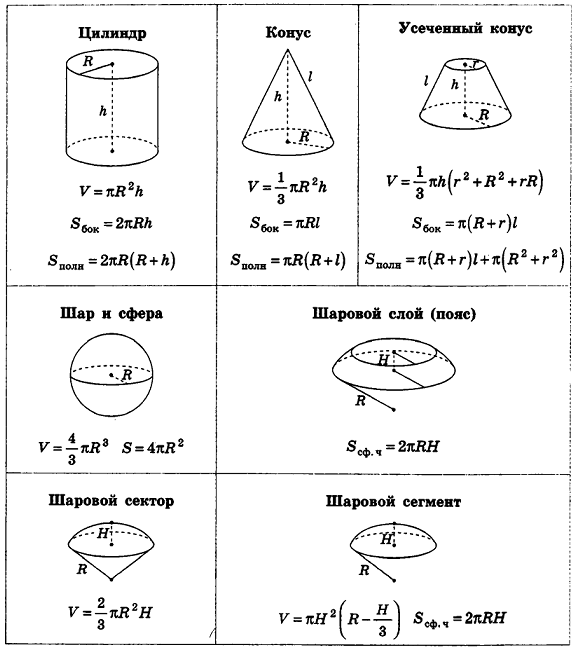
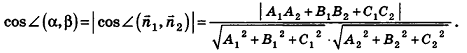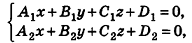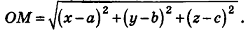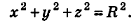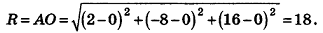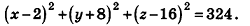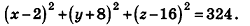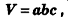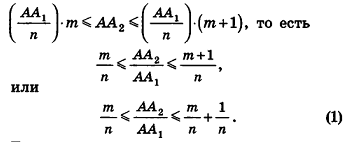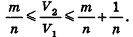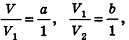Все формулы для площадей полной и боковой поверхности тел
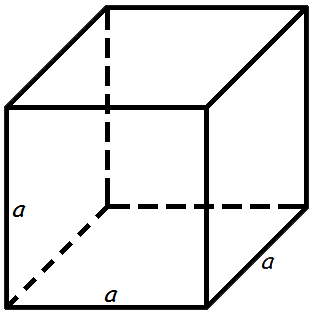
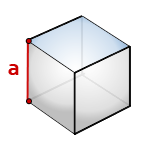
1. Площадь полной поверхности куба
a – сторона куба
Формула площади поверхности куба,(S):
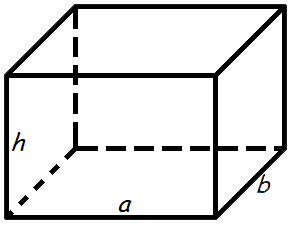
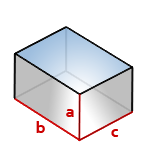
2. Найти площадь поверхности прямоугольного параллелепипеда
a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
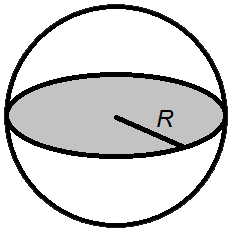
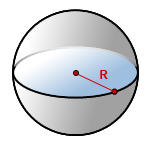
3. Найти площадь поверхности шара, сферы
R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
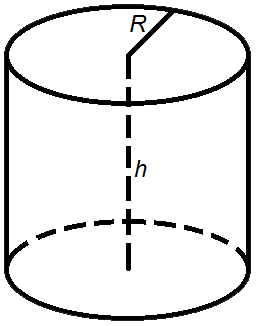
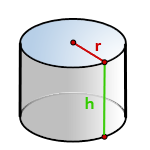
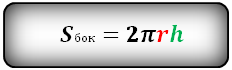
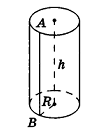
4. Найти площадь боковой и полной поверхности цилиндра
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула площади боковой поверхности цилиндра, (Sбок):
Формула площади всей поверхности цилиндра, (S):
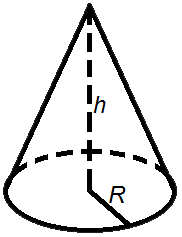
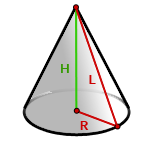
5. Площадь поверхности прямого, кругового конуса
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):
Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):
Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):
Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):
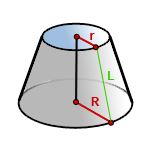
6. Формулы площади поверхности усеченного конуса
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):
Формула площади полной поверхности усеченного конуса, (S):
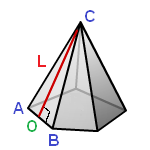
7. Площадь поверхности правильной пирамиды через апофему
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
Формула площади полной поверхности правильной пирамиды (S):
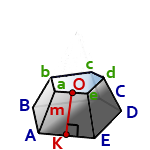
8. Площадь боковой поверхности правильной усеченной пирамиды
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
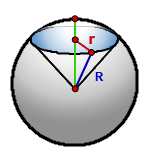
9. Площадь поверхности шарового сегмента
R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):
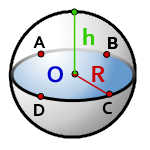
10. Площадь поверхности шарового слоя
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):
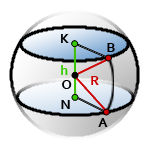
11. Площадь поверхности шарового сектора
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):
Прямой круговой цилиндр с развёрткой его боковой поверхности
Боковая поверхность — поверхность тела без его оснований. Определяется для цилиндров, конусов, усечённых конусов, призм, шаровых сегментов, шаровых слоёв и так далее.
Площадь[править | править код]
Площадь боковой поверхности может быть найдена используя следующие формулы:
- Для прямого цилиндра и призмы: произведение периметра основания на высоту.
- Для прямого кругового конуса и правильной пирамиды: произведение периметра основания на половину апофемы.
- Для усечённого прямого кругового конуса и правильной усечённой пирамиды: произведение полусуммы периметров обоих оснований на апофему.
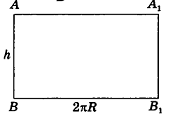
Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой 

Содержание:
Площади поверхностей геометрических тел:
Под площадью поверхности многогранника мы понимаем сумму площадей всех его граней. Как же определить площадь поверхности тела, не являющегося многогранником? На практике это делают так. Разбивают поверхность на такие части, которые уже мало отличаются от плоских. Тогда находят площади этих частей, как будто они являются плоскими. Сумма полученных площадей является приближенной площадью поверхности. Например, площадь крыши здания определяется как сумма площадей кусков листового металла. Еще лучше это видно на примере Земли. Приблизительно она имеет форму шара. Но площади небольших ее участков измеряют так, как будто эти участки являются плоскими. Более того, под площадью поверхности тела будем понимать предел площадей полных поверхностей описанных около него многогранников. При этом должно выполняться условие, при котором все точки поверхности этих многогранников становятся сколь угодно близкими к поверхности данного тела. Для конкретных тел вращения понятие описанного многогранника будет уточнено.
Понятие площади поверхности
Рассмотрим периметры
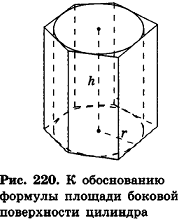
Применим данные соотношения к обоснованию формулы для площади боковой поверхности цилиндра.
При вычислении объема цилиндра были использованы правильные вписанные в него призмы. Найдем при помощи в чем-то аналогичных рассуждений площадь боковой поверхности цилиндра.
Опишем около данного цилиндра радиуса R и высоты h правильную n-угольную призму (рис. 220).
Площадь боковой поверхности призмы равна
где 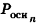
При неограниченном возрастании n получим:
так как периметры оснований призмы стремятся к длине окружности основания цилиндра, то есть к
Учитывая, что сумма площадей двух оснований призмы стремится к 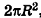
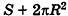
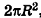
Итак, площадь боковой поверхности цилиндра вычисляется по формуле
где R — радиус цилиндра, h — его высота.
Заметим, что эта формула аналогична соответствующей формуле площади боковой поверхности прямой призмы
За площадь полной поверхности цилиндра принимается сумма площадей боковой поверхности и двух оснований:
Если боковую поверхность цилиндра радиуса R и высоты h разрезать по образующей АВ и развернуть на плоскость, то в результате получим прямоугольник 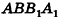
Очевидно, что сторона 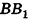
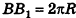
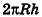
Пример:
Параллельно оси цилиндра на расстоянии d от нее проведена плоскость, отсекающая от основания дугу 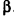
Решение:
Пусть дан цилиндр, в основаниях которого лежат равные круги с центрами 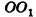
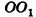
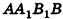
Пусть хорда АВ отсекает от окружности основания дугу 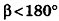
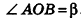
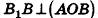
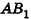
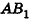
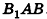
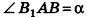
В равнобедренном треугольнике 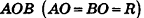
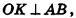
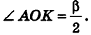
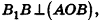
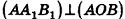
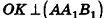
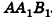
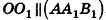
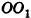
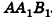
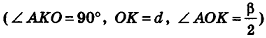
откуда 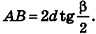
Итак,
В случае, когда
Аналогично предыдущему, и в этом случае получаем тот же результат для площади боковой поверхности.
Ответ:
Площадь поверхности конуса и усеченного конуса
Связь между цилиндрами и призмами полностью аналогична связи между конусами и пирамидами. В частности, это касается формул для площадей их боковых поверхностей.
Опишем около данного конуса с радиусом основания R и образующей I правильную л-угольную пирамиду (рис. 223). Площадь ее боковой поверхности равна
где 
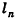
При неограниченном возрастании n получим:
так как периметры оснований пирамиды стремятся к длине окружности основания конуса, а апофемы 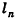
Учитывая, что площадь основания пирамиды стремится к 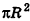
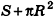
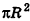
где R — радиус основания, I — образующая.
За площадь полной поверхности конуса принимается сумма площадей его основания и боковой поверхности:
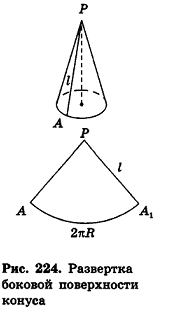
Если боковую поверхность конуса разрезать по образующей РА и развернуть на плоскость, то в результате получим круговой сектор 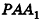
Очевидно, что радиус сектора развертки равен образующей конуса I, а длина дуги 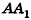
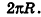
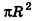
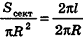
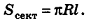
Учитывая формулу для площади боковой поверхности конуса, нетрудно найти площадь боковой поверхности усеченного конуса.
Рассмотрим усеченный конус, полученный при пересечении конуса с вершиной Р некоторой секущей плоскостью (рис. 225).
Пусть 
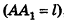
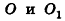
Из подобия треугольников
следует, что
Тогда получаем
Таким образом,
Итак, мы получили формулу для вычисления площади боковой поверхности усеченного конуса: 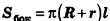
Отсюда ясно, что площадь полной поверхности усеченного конуса равна
Такой же результат можно было бы получить, если найти площадь развертки боковой поверхности усеченного конуса или использовать правильные усеченные пирамиды, описанные около него. Попробуйте дать соответствующие определения и провести необходимые рассуждения самостоятельно.
Связь между площадями поверхностей и объемами
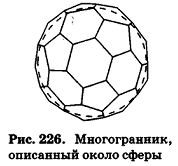
При рассмотрении объемов и площадей поверхностей цилиндра и конуса мы видели, что существует тесная взаимосвязь между этими фигурами и призмами и пирамидами соответственно. Оказывается, что и сфера (шар), вписанная в многогранник, связана с величиной его объема.
Определение:
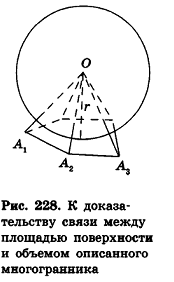
Сфера (шар) называется вписанной в выпуклый многогранник, если она касается каждой его грани.
При этом многогранник называется описанным около данной сферы (рис. 226).
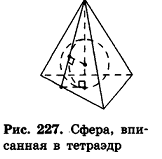
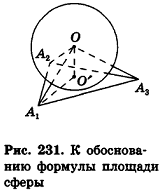
Рассмотрим, например, сферу, вписанную в тетраэдр (рис. 227).
Плоскости, содержащие грани тетраэдра, являются касательными к вписанной сфере, а точки касания лежат в гранях тетраэдра. Заметим, что по доказанному в п. 14.2 радиусы вписанной сферы, проведенные в точку касания с поверхностью многогранника, перпендикулярны плоскостям граней этого многогранника.
Для описанных многоугольников на плоскости было доказано, что их площадь равна произведению полупериметра на радиус вписанной окружности. Аналогичное свойство связывает объем описанного многогранника и площадь его поверхности.
Теорема (о связи площади поверхности и объема описанного многогранника)
Объем описанного многогранника вычисляется по формуле
где 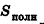
Доказательство:
Соединим центр вписанной сферы О со всеми вершинами многогранника 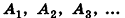
где 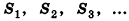
Теорема доказана.
Оказывается, что в любой тетраэдр можно вписать сферу, и только одну. Но не каждый выпуклый многогранник обладает этим свойством.
Рассматривают также сферы, описанные около многогранника.
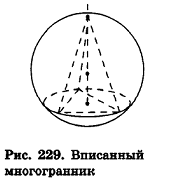
Определение:
Сфера называется описанной около многогранника, если все его вершины лежат на сфере.
При этом многогранник называется вписанным в сферу (рис. 229).
Также считается, что соответствующий шар описан около многогранника.
Около любого тетраэдра можно описать единственную сферу, но не каждый многогранник обладает соответствующим свойством.
Площадь сферы
Применим полученную связь для объемов и площадей поверхностей описанных многогранников к выводу формулы площади сферы.
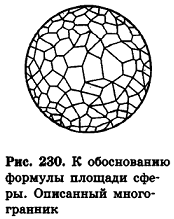
Опишем около сферы радиуса R выпуклый многогранник (рис. 230).
Пусть S’ — площадь полной поверхности данного многогранника, а любые две точки одной грани удалены друг от друга меньше чем на е. Тогда объем многогранника равен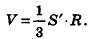
По неравенству треугольника 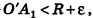
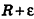
Итак, объем V данного многогранника больше объема шара радиуса R и меньше объема шара радиуса 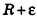
Отсюда получаем
Если неограниченно уменьшать размеры граней многогранника, то есть при е, стремящемся к нулю, левая и правая части последнего неравенства будут стремиться к 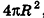
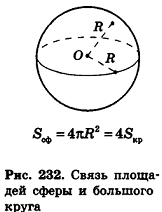
Итак, площадь сферы радиуса R вычисляется по формуле
Доказанная формула означает, что площадь сферы равна четырем площадям ее большого круга (рис. 232).
Исходя из аналогичных рассуждений, можно получить формулу для площади сферической части шарового сегмента с высотой Н:
Оказывается, что эта формула справедлива и для площади сферической поверхности шарового слоя (пояса):
где Н — высота слоя (пояса).
Справочный материал
Формулы объемов и площадей поверхностей геометрических тел
Историческая справка
Многие формулы для вычисления объемов многогранников были известны уже в Древнем Египте. В так называемом Московском папирусе, созданном около 4000 лет назад, вероятно, впервые в истории вычисляется объем усеченной пирамиды. Но четкие доказательства большинства формул для объемов появились позднее, в работах древнегреческих ученых.
Так, доказательства формул для объемов конуса и пирамиды связаны с именами Демокрита из Абдеры (ок. 460-370 гг. до н. э.) и Евдокса Книдского (ок. 408-355 гг. до н. э.). На основании их идей выдающийся математик и механик Архимед (287-212 гг. до н. э.) вычислил объем шара, нашел формулы для площадей поверхностей цилиндра, конуса, сферьГг
Дальнейшее развитие методы, предложенные Архимедом, получили благодаря трудам средневекового итальянского монаха и математика Бонавентуры Кавальери (1598-1647). В своей книге «Геометрия неделимых» он сформулировал принцип сравнения объемов, при котором используются площади сечений. Его рассуждения стали основой интегральных методов вычисления объемов, разработанных Исааком Ньютоном (1642 (1643)-1727) и Готфридом Вильгельмом фон Лейбницем (1646-1716). Во многих учебниках по геометрии объем пирамиды находится с помощью * чертовой лестницы» — варианта древнегреческого метода вычерпывания, предложенного французским математиком А. М. Лежандром (1752-1833).
На II Международном конгрессе математиков, который состоялся в 1900 году в Париже, Давид Гильберт сформулировал, в частности, такую проблему: верно ли, что любые два равновеликих многогранника являются равносоставленными? Уже через год отрицательный ответ на этот вопрос был обоснован учеником Гильберта Максом Деном (1878-1952). Другое доказательство этого факта предложил в 1903 году известный геометр В. Ф. Каган, который в начале XX века вел плодотворную научную и просветительскую деятельность в Одессе. В частности, из работ Дена и Кагана следует, что доказательство формулы объема пирамиды невозможно без применения пределов.
Весомый вклад в развитие теории площадей поверхностей внесли немецкие математики XIX века. Так, в 1890 году Карл Герман Аман-дус Шварц (1843-1921) построил пример последовательности многогранных поверхностей, вписанных в боковую поверхность цилиндра («сапог Шварца»). Уменьшение их граней не приводит к приближению суммы площадей этих граней к площади боковой поверхности цилиндра. Это стало толчком к созданию выдающимся немецким математиком и физиком Германом Минков-ским (1864-1909) современной теории площадей поверхностей, в которой последние связаны с объемом слоя около данной поверхности.
Учитывая огромный вклад Архимеда в развитие математики, в частности теории объемов и площадей поверхностей, именно его изобразили на Филдсовской медали — самой почетной в мире награде для молодых математиков. В 1990 году ею был награжден Владимир Дрин-фельд (род. в 1954 г.), который учился и некоторое время работал в Харькове. Вот так юные таланты, успешно изучающие геометрию в школе, становятся в дальнейшем всемирно известными учеными.
Уравнения фигур в пространстве
Напомним, что уравнением фигуры F на плоскости называется уравнение, которому удовлетворяют координаты любой точки фигуры F и не удовлетворяют координаты ни одной точки, не принадлежащей фигуре F. Так же определяют и уравнение фигуры в пространстве; но, в отличие от плоскости, где уравнение фигуры содержит две переменные х и у, в пространстве уравнение фигуры является уравнением с тремя переменными х, у и z.
Выведем уравнение плоскости, прямой и сферы в пространстве. Для получения уравнения плоскости рассмотрим в прямоугольной системе координат плоскость а (рис. 233) и определим свойство, с помощью которого можно описать принадлежность произвольной точки данной плоскости. Пусть ненулевой вектор 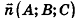
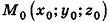
Так как 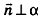
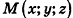
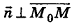
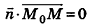
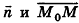
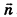
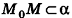
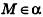
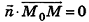
Теорема (уравнение плоскости в пространстве)
В прямоугольной системе координат уравнение плоскости имеет вид 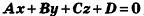
Доказательство:
Запишем в координатной форме векторное равенство 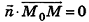
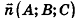
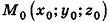
Следовательно,
После раскрытия скобок и приведения подобных членов это уравнение примет вид:
Обозначив числовое выражение в скобках через D, получим искомое уравнение, в котором числа А, В и С одновременно не равны нулю, так как 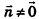
Покажем теперь, что любое уравнение вида Ах + Ву +Cz+D = 0 задает в пространстве плоскость. Действительно, пусть 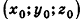
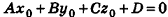
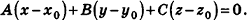
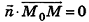
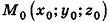
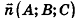
Обратим внимание на то, что в доказательстве теоремы приведен способ составления уравнения плоскости по данным координатам произвольной точки плоскости и вектора нормали.
Пример:
Напишите уравнение плоскости, которая перпендикулярна отрезку MN и проходит через его середину, если М{-1;2;3), N(5;-4;-1).
Решение:
Найдем координаты точки О — середины отрезка MN:
Значит, О (2; -1; l). Так как данная плоскость перпендикулярна отрезку MN, то вектор 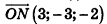
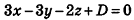
И наконец, так как данная плоскость проходит через точку О(2;-l;l), то, подставив координаты этой точки в уравнение, получим:
Таким образом, уравнение 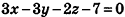
Ответ:
Заметим, что правильным ответом в данной задаче является также любое уравнение, полученное из приведенного умножением обеих частей на число, отличное от нуля.
Значения коэффициентов А, В, С и D в уравнении плоскости определяют особенности расположения плоскости в системе координат. В частности:
- если
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
- если один из коэффициентов А, В и С равен нулю, a
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
перпендикулярен оси Ох, а плоскость By + Cz + D = Q параллельна оси Ох (рис. 234, б)
- если два из коэффициентов А, В и С равны нулю, а
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
перпендикулярен плоскости Оху, а плоскость Cz+D = 0 параллельна плоскости Оху (рис. 234, в);
- если два из коэффициентов А, В и С равны нулю и D = 0, плоскость совпадает с одной из координатных плоскостей: например, при условиях
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
Предлагаем вам самостоятельно составить полную таблицу частных случаев расположения плоскости Ax + By+Cz+D = 0 в прямоугольной системе координат в зависимости от значений коэффициентов А, В, С и D.
Пример: (о расстоянии от точки до плоскости)
Расстояние от точки 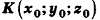
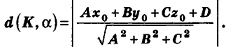
Решение:
Если 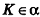
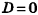
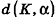
Если 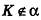
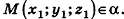
Тогда 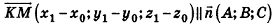
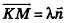
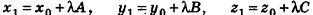
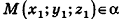
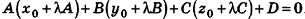
Таким образом,
Рассмотрим теперь возможность описания прямой в пространстве с помощью уравнений.
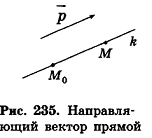
Пусть в пространстве дана прямая k (рис. 235). Выберем ненулевой вектор 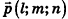
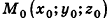
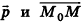
Представим это векторное равенство в координатной форме. Если ни одна из координат направляющего вектора не равна нулю, из данного равенства можно выразить t и приравнять полученные результаты:
Эти равенства называют каноническими уравнениями прямой в пространстве.
Пример:
Напишите уравнение прямой, проходящей через точки А(1;-3;2) и В(-l;0;l).
Решение:
Так как точки А и В принадлежат данной прямой, то 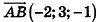
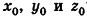
Ответ:
Заметим, что ответ в этой задаче может иметь и другой вид: так, в числителях дробей можно использовать координаты точки В, а как направляющий вектор рассматривать любой ненулевой вектор, коллинеарный 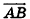
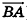
Вообще, если прямая в пространстве задана двумя точками 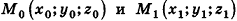
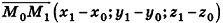
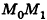
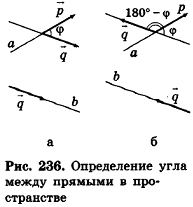
С помощью уравнений удобно исследовать взаимное расположение прямых и плоскостей в пространстве. Рассмотрим прямые 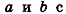
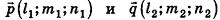
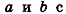
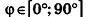
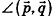
Так как cos(l80°-ф) = -coscp, имеем 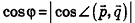
Отсюда, в частности, следует необходимое и достаточное условие перпендикулярности прямых 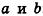
Кроме того, прямые 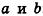
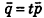
Проанализируем теперь отдельные случаи взаимного расположения двух плоскостей в пространстве. Очевидно, что если 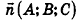
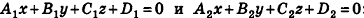
- совпадают, если существует число t такое, что
, или, если числа
ненулевые
- параллельны, если существует число t такое, что
, или, если координаты
ненулевые,
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
).
В остальных случаях данные плоскости 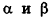
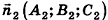
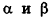
В частности, необходимое и достаточное условие перпендикулярности плоскостей 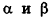
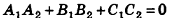
Заметим также, что прямая в пространстве может быть описана как линия пересечения двух плоскостей, то есть системой уравнений
где векторы 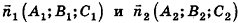
Пример:
Напишите уравнение плоскости, которая проходит через точку М(4;2;3) и параллельна плоскости x-y + 2z-S = 0.
Решение:
Так как искомая плоскость параллельна данной, то вектор нормали к данной плоскости 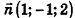
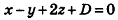
Ответ: x-y+2z-8 = 0.
Аналогично уравнению окружности на плоскости, в пространственной декартовой системе координат можно вывести уравнение сферы с заданным центром и радиусом.
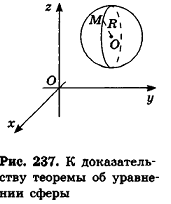
Теорема (уравнение сферы)
В прямоугольной системе координат уравнение сферы радиуса R с центром в точке 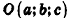
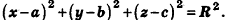
Пусть 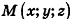
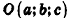
Так как OM=R, то есть ОМ2 = R2, то координаты точки М удовлетворяют уравнению 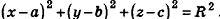
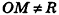
Следствие
Сфера радиуса R с центром в начале координат задается уравнением вида
Заметим, что фигуры в пространстве, как и на плоскости, могут задаваться не только уравнениями, но и неравенствами. Например, шар радиуса R с центром в точке 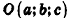
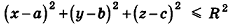
Пример:
Напишите уравнение сферы с центром А (2;-8; 16), которая проходит через начало координат.
Решение:
Так как данная сфера проходит через точку 0(0;0;0), то отрезок АО является ее радиусом. Значит,
Таким образом, искомое уравнение имеет вид:
Ответ:
Доказательство формулы объема прямоугольного параллелепипеда
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 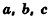
Доказательство:
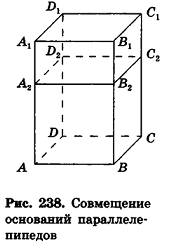
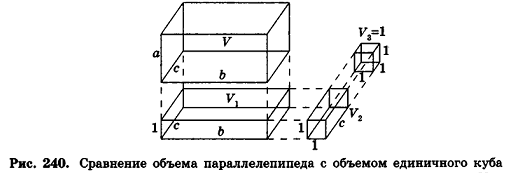
Докажем сначала, что объемы двух прямоугольных параллелепипедов с равными основаниями относятся как длины их высот.
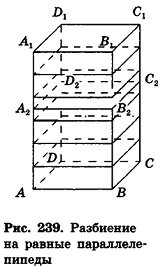
Пусть 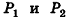
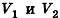
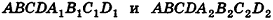
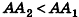
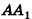
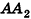
проведем через точки деления параллельные основанию ABCD (рис. 239). Они разобьют параллелепипед 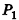
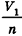
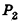
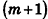
Таким образом, 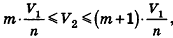
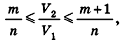
Сравнивая выражения (1) и (2), видим, что оба отношения 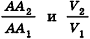
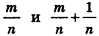
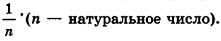
Допустим, что это не так, то есть 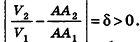
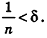
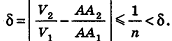
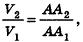
Рассмотрим теперь прямоугольные параллелепипеды с измерениями 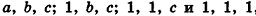
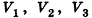
По аксиоме объема V3 =1. По доказанному 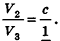
Теорема доказана.
* Выберем 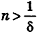
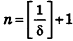
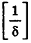
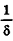
- Вычисление площадей плоских фигур
- Преобразование фигур в геометрии
- Многоугольник
- Площадь многоугольника
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
Формулы площади поверхности геометрических фигур
Площадь геометрической фигуры
– численная характеристика геометрической фигуры, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба:
S = 6 a2
где S – площадь куба,
a – длина грани куба.
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
S = 2(a · b + a · h + b · h)
где S – площадь прямоугольного параллелепипеда,
a – длина,
b – ширина,
h – высота.
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра:
S = 2 π R h
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра:
S = 2 π R h + 2 π R 2 = 2 π R(R + h)
где S – площадь,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592.
Площадь конуса
Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π.
Формула площади боковой поверхности конуса:
S = π R l
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
S = π R2 + π R l = π R (R + l)
где S – площадь,
R – радиус основания конуса,
l – образующая конуса,
π = 3.141592.
Площадь шара
Формулы площади шара:
-
Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π.
S = 4 π R2
-
Площадь поверхности шара равна квадрату его диаметра умноженного на число π.
S = π D2
где S – площадь шара,
R – радиус шара,
D – диаметр шара,
π = 3.141592.
Продолжаем повторять формулы стереометрии, на этот раз площадь поверхности. Площадь поверхности любой пространственной фигуры — это сумма всех площадей её граней. Если простыми словами – это площадь той поверхности, которую можно потрогать у фигуры.
✅ Начнём с куба — у него шесть граней, все они квадраты, поэтому площадь каждой равна a^2, а площадь поверхности куба равна 6 • a^2. У прямоугольного параллелепипеда примерно та же история, у него 6 граней, только на этот раз грани — 3 пары прямоугольников. Поэтому формула площади поверхности будет состоять из суммы трёх пар площадей прямоугольников: Sпр = 2 • (ab + bc + ac).
💁🏻♂ Площадь полной поверхности призмы состоит из суммы боковой поверхности и двух площадей основания. С основаниями все более менее понятно, а вот площадь боковой поверхности можно вычислить аж по двум формулам. Первая из них для прямой призмы, а вторая для наклонной призмы.
📌 У прямой призмы все грани — прямоугольники с одинаковой стороной в виде высоты. А вторая сторона каждого прямоугольника — сторона основания многоугольника в основании. Поэтому площадь боковой поверхности прямой призмы можно вычислить как произведение периметра основания на высоту.
📌 У наклонной призмы все грани — параллелограммы, поэтому базовый способ для нахождения площади поверхности — считать каждую грань по отдельности и суммировать все грани. Но это не сильно действенный способ потому, что долго и дорого так делать на экзамене, в задачах чаще всего работает другая формула.
✅ Площадь боковой поверхности наклонной призмы равна произведению бокового ребра на периметр перпендикулярного сечения этому ребру. То есть по сути это та же формула, что и для прямой призмы, только вместо периметра основания используем периметр перпендикулярного сечения, а вместо высоты используем ребро.
👉🏻 Последняя из действенных формул — площадь боковой поверхности правильной пирамиды. Площадь полной поверхности равна сумме площадей боковой поверхности и основания. Все грани правильной пирамиды – равные треугольники, у которых одинаковая высота в виде апофемы боковой грани, и равные стороны основания.
🌟 Поэтому площадь боковой поверхности равна произведению полупериметра на апофему. Одна вторая здесь возникает из-за того, что это коэффициент в каждой площади треугольника грани.
На ЕГЭ нет подсказок в виде формул, поэтому сохраняй картинку, запоминай формулы и применяй их к задачам💕
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
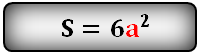

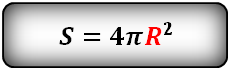






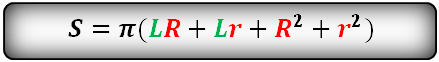
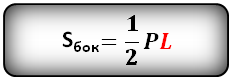
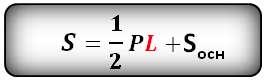
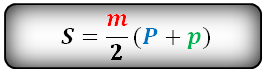




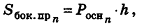
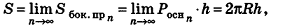
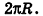
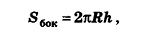
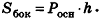
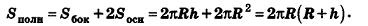

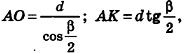
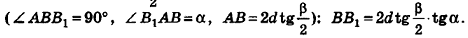
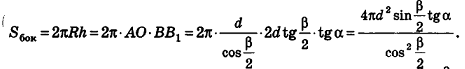
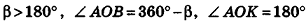
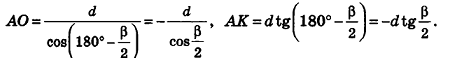
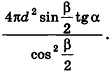
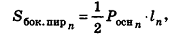
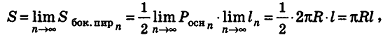
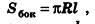
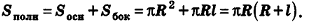
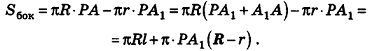
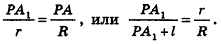
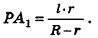
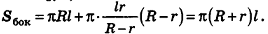
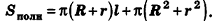
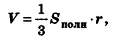
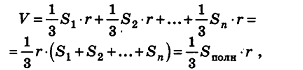
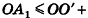
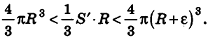
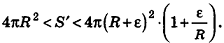
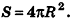
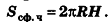
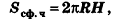






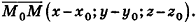
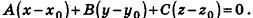
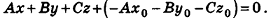
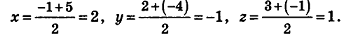
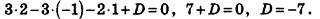
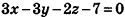
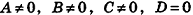 , уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);
, уравнение плоскости примет вид Ax+By+Cz = 0; очевидно, что такая плоскость проходит через начало координат (рис. 234, а);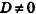 , плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали
, плоскость параллельна одной из координатных осей: например, при условии А = 0 вектор нормали 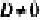 , плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали
, плоскость параллельна одной из координатных плоскостей: например, при условиях А = 0 и В-О вектор нормали 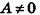 и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).
и В = С = D = 0 уравнение плоскости имеет вид Ах = О, или х= 0, то есть является уравнением плоскости Оуz (рис. 234, г).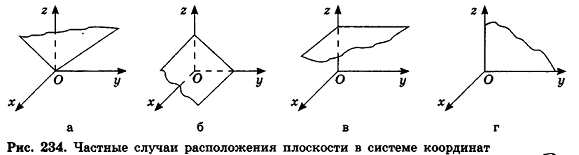
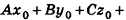
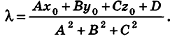
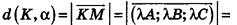
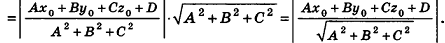
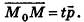
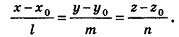
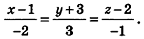
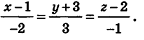
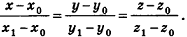
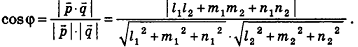
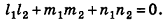
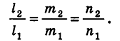
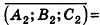
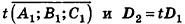 , или, если числа
, или, если числа 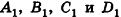 ненулевые
ненулевые 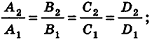
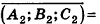
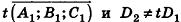 , или, если координаты
, или, если координаты 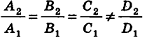 (на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где
(на практике это означает, что уравнения данных плоскостей можно привести к виду Ax+By+Cz+D1= 0 и Ax+By+Cz+D2=0, где 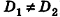 ).
).