Как найти площадь боковой поверхности пирамиды хеопса

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Пирамида
  понятие
  виды
  свойства
  Учитель математики МОУ Кузнечихинская СШ ЯМР
  Увава Е.А.

• 

  2 слайд

  Цель урока:

  Изучить новый вид многогранников – пирамида
  Выйти на понятие правильной пирамиды, усечённой пирамиды
  Изучить свойства пирамиды

• 

  3 слайд

  А2
  А3
  Р
  Многоугольник состоящий из n – угольника РА1А2…Аn и n треугольников называется пирамидой
  Многогранник А1А2…Аn называется основанием
  Треугольники РА1А2, РА2 А3 , … называются боковыми гранями
  Аn
  А1

• 

  4 слайд

  А1
  Р
  А2
  А3
  Прямые РА1, РА2, РА3, … называются боковыми рёбрами пирамиды

  О
  Перпендикуляр РО, опущенный из вершины на основание называются высотой пирамиды

  Р – вершина пирамиды

• 

  5 слайд

  Пирамида называется n – угольной, если в её основании лежит n – угольник

  Треугольная
  (Тетраэдр)
  Четырёхугольная
  Пятиугольная
  Шестиугольная

• 

  6 слайд

  А
  В
  С
  S
  A1
  В1
  С1
  (А1В1С1) || (АВС)

  Пирамида SАВС подобна пирамиде SА1В1С1
  А
  В
  С
  S
  A1
  В1
  С1
  Доказательство

  Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает подобную пирамиду
  Теорема

• 

  7 слайд

  Пирамида называется правильной, если её основанием является правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
  S
  С
  А
  В
  D
  У правильной пирамиды боковые рёбра равны
  Боковые грани правильной пирамиды – равнобедренные треугольники, равные между собой
  Высота боковой грани правильной пирамиды , проведённая из её вершины, называется апофемой

  О
  Е
  Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.
  Sбок. = р l
  Доказательство:

• 

  8 слайд

  Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением.
  Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники.
  Сечения пирамиды
  М
  N
  К
  L
  S
  А
  В
  С
  D
  Р
  R
  F

• 

  9 слайд

  Если пирамиду пересечь плоскостью, параллельной плоскости основания, то:

  а) боковые ребра и высота делятся этой плоскостью на пропорциональные части в отношении

  б) в сечении образуется многоугольник, подобный основанию пирамиды;
  (О1А1В1С1 подобен ОАВС)

  в) площади сечения и основания пирамиды относятся как квадраты их расстояний до вершины пирамиды:

  Р
  О
  А
  С
  В
  О1
  А1
  В1
  С1
  S 1
  S 2
  H
  H1

• 

  10 слайд

  Часть пирамиды, лежащая между основанием и параллельным основанию сечением, называется
  усеченной пирамидой
  Грани усечённой пирамиды, лежащие в параллельных плоскостях называются основаниями пирамиды
  Основания усеченной пирамиды – подобные многоугольники
  Высота усеченной пирамиды – это общий перпендикуляр к плоскостям ее оснований (или его длина).
  Усечённая пирамида, полученная из правильной пирамиды – правильная
  Боковые грани правильной усечённой пирамиды – равные равнобокие трапеции, а их высоты называются апофемами

  О
  А
  С
  В
  О1
  С1
  А1
  В1
  Н
  Е
  Теорема. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров основания на апофему
  S бок = (Р1 + Р2 ) · l
  Доказательство:

• 

  11 слайд

  A
  B
  C
  S
  SABC – тетраэдр 
  3.Чему равна площадь поверхности правильного тетраэдра с ребром 1?
  Решение
  1. Sпов=4Sтр
  2. Sтр = 0,5а2sin600
  Ответ:
  3. Sпов=4 • 0,5а2sin600 =
  =

• 

  12 слайд

  4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230 м и высота 138 м.
  О
  E
  S
  D
  С
  В
  А
  Решение:
  2. AC  ВD = О
  3. Пирамида правильная 
  SО  (АВС)
  4. ОЕ  СD  ОЕ  АD 
  5. SЕ  АD (по теореме о 3 перпендикулярах)
  6.  SОЕ – пу
  по т. Пифагора
  ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
  = 13225 +19044 = 32269
  ЕS  180
  7. ES – высота АSD
  SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2
  Ответ: 82800 м2
  1. Sб.пов=4Sтр
  8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2

• 

  13 слайд

  3. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.
  В
  А
  С
  S
  К
  Р
  F
  1. РК
  2. КF
  3. КF  SС = N
  N
  4. РN  ВС = D
  D
  5. DF
  6. PKFD – искомое

• 

  14 слайд

  Домашнее задание
  1). Если в правильной треугольной пирамиде высота H равна стороне основания a, то боковые ребра составляют с плоскостью основания углы в 600. Верно ли это утверждение?
  2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см.
  3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».

• 

  15 слайд

  Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.
  М
  N
  K
  A
  B
  C
  D
  S
  Домашнее задание

Краткое описание документа:

В данной подборке представлен материал по теме «Пирамида» для учителей, работающих по
учебнику «Геометрия», Л. С.Атанасян,
В.Ф.Бутузов, и др.: презентация к уроку
по теме «Пирамида», доказательства
теорем по данной вынесено в отдельную презентацию, что позволяет использовать их на уроке по
усмотрению учителя; интерактивный тест по теме «Пирамида», подборка задач,
которые можно использовать на уроке для решения по готовым чертежам.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 251 183 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.

Что собой представляет пирамида?

Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой. Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.

Два важных элемента любой пирамиды — это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.

Поверхность пирамиды

Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.

Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры — это сумма площадей каждой ее стороны.

Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.

Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.

Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.

Площадь боковой поверхности четырехугольной правильной пирамиды

Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника. Из курса геометрии известно, что треугольника площадь S_t равна произведению основания на высоту, которое следует поделить пополам. То есть:

S_t = 1/2*h_b*a.

Где h_b — высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь S_b поверхности боковой для рассматриваемой пирамиды:

S_b = 4*S_t = 2*h_b*a.

Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы h_b для двух случаев:

• когда известна длина бокового ребра;
• когда известна высота пирамиды.

Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема h_b определиться по формуле:

h_b = √(L² — a²/4).

Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.

Если известна высота h пирамиды, тогда апотему h_b можно рассчитать так:

h_b = √(h² + a²/4).

Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой h_b.

Покажем, как применять эти формулы, решив две интересные задачи.

Задача с известной площадью поверхности

Известно, что площадь боковой поверхности четырехугольной пирамиды правильной равна 108 см². Необходимо вычислить значение длины ее апотемы h_b, если высота пирамиды равна 7 см.

Запишем формулу площади S_b поверхности боковой через высоту. Имеем:

S_b = 2*√(h² + a²/4) *a.

Здесь мы просто подставили соответствующую формулу апотемы в выражение для S_b. Возведем обе части равенства в квадрат:

S_b² = 4*a²*h² + a⁴.

Чтобы найти значение a, сделаем замену переменных:

a² = t;

t² + 4*h²*t — S_b² = 0.

Подставляем теперь известные значения и решаем квадратное уравнение:

t² + 196*t — 11664 = 0.

t ≈ 47,8355.

Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:

a = √t = √47,8355 ≈ 6,916 см.

Чтобы получить длину апотемы, достаточно воспользоваться формулой:

h_b = √(h² + a²/4) = √(7² + 6,916²/4) ≈ 7,808 см.

Боковая поверхность пирамиды Хеопса

Определим значение площади поверхности боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для S_b, получим:

S_b = 2*√(h² + a²/4) *a = 2*√(146,5²+230,363²/4)*230,363 ≈ 85860 м².

Найденное значение немного больше площади 17 футбольных полей.

Просмотры: 53

Тема: «Площадь поверхности и объем пирамиды»

Цель: ознакомление обучающихся с формулами для вычисления площадей полной поверхности и боковой поверхности пирамиды, объема;

Теоретический материал

1. Актуализания знаний

Оформите данные рисунки в тетрадь и определите вид каждой пирамиды

   

1. Историческая справка:

Одна из версий происхождения термина пирамида утверждает, что название происходит от греческого слова«пир» огонь т.к. форма пирамиды напоминает форму пламени. Египетские пирамиды – одно из семи чудес света. Усыпальницы фараонов. Крупнейшие из них это пирамиды Хеопса, Хефрена, Микерина в Гизе. Самая большая из них пирамида Хеопса. Высота изначально 147м. Длина стороны основания 232м.Вес 6400000т.До 1889г. была самым высоким зданием пока не построили Эйфелеву башню. Показываю слайд с изображением пирамиды Хеопса . Мало кто знает, что при постройке египетской пирамиды было установлено, что квадрат, построенный на высоте пирамиды в точности равен площади каждого из боковых треугольников. Это подтверждается и новейшими измерениями. Если сторону основания пирамиды разделить на точную длину года 365,2422 суток, то получится 10- миллионная доля земной полуоси с большой точностью. Если сложить 4 стороны основания пирамиды Хеопса, мы получим 931,22м. Разделив это число на удвоенную высоту пирамиды (2٠148,208)м. мы получим 3.14 т. е. число 𝜋. Показываю слайд (пирамида Хеопса внутри). В строительстве часто используют пирамидальную форму(показ слайдов : здание в Лондоне, пирамида перед Лувром, дом)

1. Изучение нового материала

 А теперь решим такую задачу: Представьте, что нам надо покрыть железом крышу дома, которая имеет форму правильной 4- угольной пирамиды. Апофема пирамиды 10м. Сторона основания 12м. Какие грани будут покрываться железом? Покажите их на развёртке. Т.е. нам надо узнать площадь боковой поверхности правильной пирамиды. Сколько боковых граней у данной пирамиды?. Какими фигурами являются боковые грани(равнобедренные равные треугольники) следовательно Sбок= 4S∆ Как найти площадь треугольника: .Чему равна будет площадь боковой поверхности нашей пирамиды?

Sбок=  значит Sбок=2٠12٠10=240м2 . Ответ:240м2. что мы сейчас нашли? А как вы думаете, что будет из себя представлять полная поверхность пирамиды?

Запишем в тетрадь формулу для вычисления полной поверхности пирамиды Sп = Sбок + Sосн . Какой фигурой могут быть основания пирамиды?

Какой фигурой являются боковые грани любой пирамиды? Значит надо уметь вычислять площади треугольников, 4- угольников (ромб, трапеция, квадрат, прямоугольник, параллелограмм) А теперь вернёмся к нашей задаче 4а – это периметр основания пирамиды, h = d – апофема. Сформулируем и запишем формулу для вычисления боковой поверхности правильной пирамиды: Sбок=  росн٠h Таким образом боковая поверхность правильной пирамиды равна половине произведения периметра основания на апофему т.е. высоту боковой грани.

Если пирамида неправильная, то как придётся вычислять площадь такой пирамиды?

1. Выполнение практической части

Нахождение поверхности пирамиды является практически необходимым в жизни человека, например в строительстве.

Решить задачу: Пирамида Хеопса имеет следующие размеры, они представлены в таблице. Найти площадь боковой поверхности пирамиды Хеопса.

Таблица 1 Пирамида Хеопса

Длина стороны основания (а)	Высота боковой грани- апофема (h)	Периметр основания Росн.	Sбок
230м.	180м.	920м.	?

Представьте себе, что вы работаете на предприятии, которое изготавливает упаковки для молока в форме тетраэдра, вместимостью 0,5л. Надо рассчитать количество материала для изготовления 1 коробки. Размеры: грани коробки представляют собой правильные треугольники со стороной 12см. и высотой – 10см.

Таблица 2 упаковка для молока. Определить площадь поверхности упаковки, имеющей форму правильного тетраэдра.

Сторона грани (а)	Высота грани (h)	S1 площадь одной грани	Sполной пов.
12см.	10см.	?	?

1. Ответьте на следующие вопросы:

1. Сколько граней, боковых рёбер у n – угольной пирамиды?

2.Какое наименьшее число граней может иметь пирамида?

3. Высота пирамиды равна 8см. Чему равно расстояние от вершины пирамиды до основания.(рис.выполнить)

4. Боковые рёбра пирамиды равны соответственно 7,12,5см. Одно из них перпендикулярно к плоскости основания. Чему равна высота пирамиды?

1. Объем пирамиды.

Пример задачи:

Требования к отчетности:

1. Оформить конспект, выполнить все необходимые задания в рабочей тетради;
2. Фотографировать готовые решения;
3. Присылать на почту: vismyt89@mail.ru своевременно (подписывайте ФИО и номер группы), можно в ВКонтакте.

Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.

Что собой представляет пирамида?

Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой. Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.

Вам будет интересно:Ставропольский региональный многопрофильный колледж: адрес, факультеты, условия поступления и педсостав

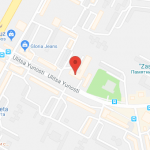
Два важных элемента любой пирамиды – это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.

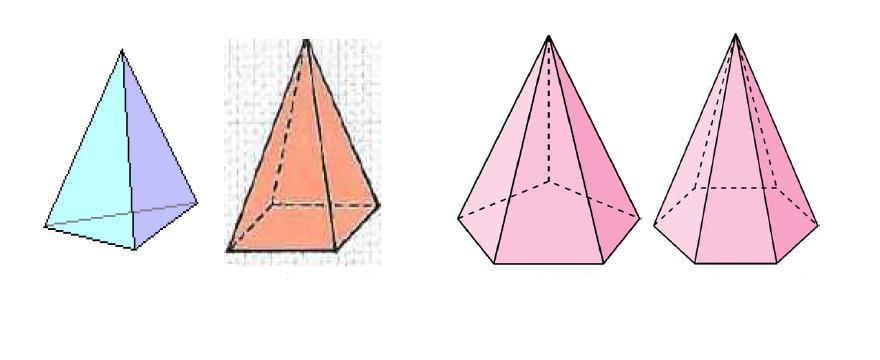
Поверхность пирамиды

Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.

Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры – это сумма площадей каждой ее стороны.

Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.

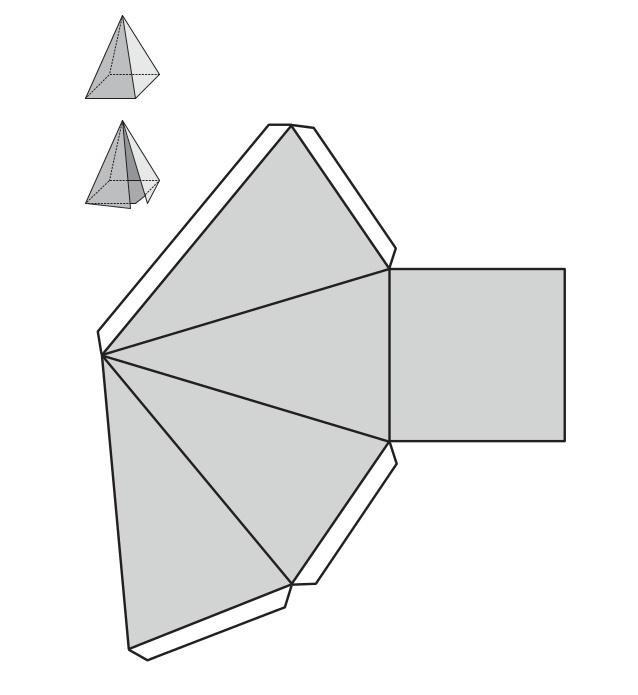
Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.

Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.

Площадь боковой поверхности четырехугольной правильной пирамиды

Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника. Из курса геометрии известно, что треугольника площадь St равна произведению основания на высоту, которое следует поделить пополам. То есть:

St = 1/2*hb*a.

Где hb – высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь Sb поверхности боковой для рассматриваемой пирамиды:

Sb = 4*St = 2*hb*a.

Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы hb для двух случаев:

• когда известна длина бокового ребра;
• когда известна высота пирамиды.

Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема hb определиться по формуле:

hb = √(L2 – a2/4).

Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.

Если известна высота h пирамиды, тогда апотему hb можно рассчитать так:

hb = √(h2 + a2/4).

Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой hb.

Покажем, как применять эти формулы, решив две интересные задачи.

Задача с известной площадью поверхности

Известно, что площадь боковой поверхности четырехугольной пирамиды правильной равна 108 см2. Необходимо вычислить значение длины ее апотемы hb, если высота пирамиды равна 7 см.

Запишем формулу площади Sb поверхности боковой через высоту. Имеем:

Sb = 2*√(h2 + a2/4) *a.

Здесь мы просто подставили соответствующую формулу апотемы в выражение для Sb. Возведем обе части равенства в квадрат:

Sb2 = 4*a2*h2 + a4.

Чтобы найти значение a, сделаем замену переменных:

a2 = t;

t2 + 4*h2*t – Sb2 = 0.

Подставляем теперь известные значения и решаем квадратное уравнение:

t2 + 196*t – 11664 = 0.

t ≈ 47,8355.

Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:

a = √t = √47,8355 ≈ 6,916 см.

Чтобы получить длину апотемы, достаточно воспользоваться формулой:

hb = √(h2 + a2/4) = √(72 + 6,9162/4) ≈ 7,808 см.

Боковая поверхность пирамиды Хеопса

Определим значение площади поверхности боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для Sb, получим:

Sb = 2*√(h2 + a2/4) *a = 2*√(146,52+230,3632/4)*230,363 ≈ 85860 м2.

Найденное значение немного больше площади 17 футбольных полей.

Египетские пирамиды: загадки архитектуры.

Пирамиды Е гипта – единственное из сохранившихся чудес света и одни из самых загадочных сооружений в истории Земли. Говоря об архитектуре Египта нельзя пройти мимо пирамид, поскольку они представляют из себя самые выдающиеся памятники древней культуры Египта. Я хочу взглянуть на пирамиды с точки зрения архитектуры. Рассматривать архитектуру пирамид, с моей точки зрения, нельзя в отрыве от их назначения, поскольку пирамиды – это невероятно сложные сооружения и каждая деталь в них не случайна, а служит реализации того предназначения, ради которого и создавались эти поразительные сооружения.

Среди большого числа всех известных египетских пирамид есть 6 , которые резко отличаются от всех остальных. В чём отличие? В том, что общие размеры, размеры отдельных блоков значительно больше, внутреннее устройство сложнее, технологии строительства этих пирамид несоизмеримо совершеннее всех остальных. Именно эти пирамиды вызывают интерес исследователей и таят в себе много вопросов:

● пирамиды на плато Гизе: Хеопса (Хуфу), Хефрена, Микерина (Менкаура):

Пирамиды на плато Гизе (вид с юга).

Пирамиды на плато Гизе – реконструкция (вид с востока).

Пирамиды на плато Гизе (карта).

● пирамида в Мейдуме:

● Ломаная пирамида Снофру в Дашуре:

● Красная (розовая) пирамида Снофру:

Египетские пирамиды хранят в себе множество тайн, которые до сих пор остаются неразгаданными. Обычные люди и учёные из различных областей науки на протяжении особенно последних десятилетий работают над разгадкой пирамид. К настоящему времени существует множество версий-гипотез касательно того, для какой цели и каким образом строили пирамиды. Но ни одна из них не может в полной мере объяснить все детали общей картины. Сразу скажу, что в этой статье я не буду говорить о совсем фантастических гипотезах некоторых учёных с богатой фантазией. Но в то же время я и не склонен не замечать очевидных фактов, которые официальная наука по какой-то причине замалчивает.

Неразгаданными и вызывающими горячие споры являются 2 вопроса: ” для чего ?” и ” каким образом ?” были созданы египетские пирамиды.

На данный момент существуют следующие наиболее распространённые реалистичные гипотезы о назначении египетских пирамид :

● Гробницы фараонов. Принимая в расчёт все известные на сегодняшний день факты (читайте ниже), эта официальная версия оказывается наименее достоверной. Если уж пирамиды и служили сооружением для захоронения, то очень и очень технологичным сооружением. Поражает сложность внутренних ходов и камер пирамид (особенно Хеопса). Эти “ходы” построены так, что ходить по ним как раз практически нереально. К тому же во всех выше указанных пирамидах отсутствуют какие-либо надписи, указывающие на то, что это гробница, и кто в ней похоронен.

● Сакральные культовые сооружения для проведения ритуалов, мистерий, обрядов и т.п. Это могла быть не основная, а второстепенная, дополнительная функция пирамид;

● Антенна – устройство для связи – передачи и приёма информации из космоса (как говорят некоторые египетские древние тексты, назначение пирамид – связь с Богами);

● Энергетические сооружения , каким-то образом взаимодействующие с энергиями Земли и Космоса (концентрируют / трансформируют / передают энергию). Греческое слово «пирамидос» переводится как “огонь посередине”, так что связь назначения пирамид с энергией заложена в самом их названии. Вопрос в том, с какой/какими энергиями пирамида работает и каким образом;

● Защита Земли от природных катаклизмов . По этой версии египетские пирамиды работали не самостоятельно, а как часть всемирной системы, включающей сотни пирамид по всей Земле;

В случае с египетскими пирамидами наиболее красноречивыми являются не те факты о пирамидах, которые нам известны и понятны, а те, которые выбиваются из общей картины, выходят за границы нашего понимания:

► ни в одной из этих пирамид не было обнаружено никаких захоронений , что ставит под сомнение теорию о пирамидах, как усыпальницах.

► отдельные части и конструкции пирамид строились из каменных блоков огромного размера и массы (до нескольких десятков тонн). Такие блоки добыть, обработать с точностью до 1-2 мм, доставить и установить на необходимую высоту – неимоверно сложная (если не невыполнимая) задача даже на современном техническом уровне. Такие блоки использовались при строительстве не только пирамид, но и храмов:

► Точность обработки отдельных блоков, а также правильность геометрии всей пирамиды, на столько высоки, что у современных учёных нет вообще идей о том, как этого можно добиться.

Флиндерс Петри: “Средняя погрешность при разрезе блоков в сравнении с теоретической прямой линией или квадратом составляет около 0,010 дюйма при длине 75 дюймов”, или 0,254 мм при длине 1,90 м. Чтобы получить такой уровень точности, необходимо было иметь соответствующие инструменты и разработать методы для измерения: речь идет о погрешности 0,00013 к 1. Петри измерил размеры самой пирамиды и, очевидно, обнаружил ошибку всего в 20 см между сторонами ее основания, чтобы получился идеальный квадрат со стороной 230,30 м. Кроме того, средняя погрешность между углами пирамиды составляет 0 3’6″, а ошибка в ориентации ее сторон относительно четырех сторон света также равна 0 3’6″.

► все предлагаемые технологии возведения пирамид – то есть то, каким образом египтяне поднимали и укладывали блоки на нужную высоту, да ещё и с феноменальной точностью – не выдерживают вдумчивого и всестороннего анализа. ( с гипотезами о технологиях возведения пирамид можно ознакомиться здесь ). А главное, это всё лишь теории, которые не были подтверждены на практике:

Пирамиды Египта представляют неимоверно сложное с точки зрения архитектуры сооружения. Измерения и экспериментальные современные исследования выявили множество закономерностей в геометрии пирамид, которые в своей совокупности никак не могли быть случайностью. Создатели пирамид осознанно заложили их в конструкцию. На мой взгляд, именно глубокое изучение и понимание следующих фактов способно дать верный ответ на вопрос зачем строили пирамиды:

► Пирамиды сориентированы на магнитные полюса Земли с очень большой точностью ( ошибка в ориентации ее сторон равна 3’6″ ). Эта точность не могла быть случайностью, и такая строгая ориентация, вероятно, играет значимую роль в назначении пирамид.

► египетские пирамиды (а также другие пирамиды по всему миру) расположены в местах выхода геомагнитной энергии. Из этого следует, что назначение пирамид каким-то образом связано с этой энергией.

► существуют гипотезы (подтвердить или опровергнуть их очень трудно), что пирамиды Египта (а также Мексики и Китая) ориентированы определённым образом на звёзды. Астрономия в Египте была развита на высоком уровне, поэтому данная гипотеза выглядит очень правдоподобной. Если говорить о пирамидах на плато Гизе, то они связаны с Сириусом и созвездием Орион, которое занимает важное место в религии Египта. Так расположение пирамид на плато совпадает с расположение звёзд в поясе Ориона, а шахты пирамиды Хеопса направлены на эти звёзды в знаковые периоды времени:

► Пропорции отдельных элементов пирамид демонстрируют все универсальные (космические) математические законы, известные людям: золотое сечение Ф , а также число Пи .

Принципу Золотого Сечения подчинено всё, что связано с природными системами – это пропорции человеческого тела, структура генетического кода – молекул ДНК и РНК, по этому принципу построены звуковой и цветовой ряды, система химических элементов и периоды обращения планет Солнечной системы, и т.д., и т.п. Всё, что даёт человеку ощущение гармонии, создано по этому «золотому принципу».

В пирамиде Хеопса принцип Золотого Сечения отражён в прямоугольном треугольнике сечения по оси симметрии в вертикальной плоскости – FOE . Он называется египетский треугольник (также треугольник Кеплера):

Рассмотрим это на размерах пирамиды Хеопса (размеры приблизительные, поскольку разные учёные имели разное мнение по поводу того, как измерять пирамиду, так что их размеры различны):

– найдём высоту уклона ( h );

( высота пирамиды H=146.515 м, основание АВ=230,363 м)

– половина основания g =230,363/2=115,182 м;

– следовательно hІ =146,515 І + 115,182 І = 34733 м;

– h =√34733 = 186,369 м;

– h / g = 186,369 / 115,182 = 1,618 = Ф

Египетский треугольник таким образом имеет основание равное 1, а его гипотенуза равна Ф. Его высота по теореме Пифагора вычисляется как √Ф.

Стороны египетского треугольника ( FOE ) находятся в соотношении: 1 / √Ф / Ф

Отношение полупериметра основания пирамиды к высоте очень близко к числу Пи :

230,363*2 / 146,515 = 3,144565.

периметр основания пирамиды Хеопса равняется окружности круга, чей радиус равен высоте пирамиды:

– периметр основания = 4 * 2 = 8;

– длина окружности с R= √Ф равна 2π√Ф = 7,992;

– погрешность сравнения периметра квадрата и окружности – менее 0,1%.

Вычислим отсюда значение π: 4/ √Ф=3,1446,

это значение также отличается от принятого значения числа Пи лишь на 0,1%.

Гипотеза:

Пирамида, построенная по принципу Золотого Сечения генерирует своей формой особое торсионное поле, которое гармонизирует окружающее пространство, определённым образом воздействуя на всё, что находится в зоне его влияния. Здесь можно говорить о раскрытии потенциала человека посредством нахождения в тех или иных потоках энергии, аккумулируемых различными зонами сакральных модулей (пирамид). С помощью таких модулей можно воспринимать, усиливать, направлять и проявлять энергоинформационные потоки, а также получать информацию из Космоса в неискажённом виде. Более того, пирамиды и иные сакральные структуры, объединённые с сознанием, способны восстанавливать здоровье и экосистему планеты.

Какой бы ни была реальная цель постройки пирамид, очевидно одно – великие сооружения строятся под великие задачи. Усилия, затраченные на сооружение пирамид, колоссальны, а значит, цель должна была быть неимоверна значима.

Как бы нам ни было это неприятно, но стоит признать, что на нынешнем уровне развития нашей цивилизации, определение истинного назначения египетских пирамид во всей полноте и точности – просто невыполнимая задача. Мы можем выдвигать тысячи правдоподобных гипотез, но само обилие этих гипотез подтверждает, что точно мы ничего сказать не можем. Возможно, что отдельные личности смогли разгадать тайну пирамид, но их версии не будут признаны общественностью до тех пор, пока всё общество не дорастёт до их уровня.

Пирамида хеопса как треугольник

Чудо – Рациональность – Наука – Духовность

Ж ИЗНЕННЫЙ ПУТЬ – это путь исследователя, постигающего тайны мироздания

Наш сайт доступен на 52 языках

Тайны Египетских Пирамид

Бесконечное, однообразное море песка, редкие высохшие кустики растений, едва заметные следы от прошедшего верблюда заметает ветер. Раскаленное солнце пустыни. И оно кажется тусклым, словно покрыто мелким песком.

И вдруг, словно мираж, перед изумленным взором возникают пирамиды (Рис.1) – фантастические фигуры из камня, устремленные к Солнцу. Своими громадными размерами, совершенством геометрической формы они поражают воображение. Согласно многим описаниям, эти гигантские монолиты имели раньше совершенно иной вид, чем в наше время. Они сияли на солнце белой глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов. Рядом с царскими пирамидами стояли пирамиды жен и членов семьи фараонов.

Рисунок 1. Комплекс пирамид в Гизе.

Власть фараона в Древнем Египте была огромной, ему воздавали божественные почести, называли “Большим Богом”. Бог-фараон был покровителем страны, вершителем судеб народа. Культ умершего фараона приобретал огромное значение в египетской религии. Для сохранения тела фараона и его духа и возвеличивания власти фараона сооружали гигантские пирамиды. И недаром эти творения рук человеческих относили к одному из семи чудес света.

Назначение пирамид было многофункциональным. Они служили не только усыпальницами фараонов, но и являлись атрибутами величия, могущества и богатства страны, памятниками культуры, хранилищами истории страны и сведений о жизни фараона и народа, собранием предметов быта.

Совершенно ясно, что пирамиды имели глубокое “научное содержание”, воплощенное в их форме, размерах и ориентировке на местности. Каждая деталь пирамиды, каждый элемент формы выбирались тщательно и должны были продемонстрировать высокий уровень знаний создателей пирамид. Ведь они строились на тысячелетия, “навечно”. И недаром арабская пословица гласит: “Все на свете страшится времени. Время страшится пирамид”.

Среди грандиозных пирамид Египта особое место занимает Великая Пирамида фараона Хеопса (Хуфу). Прежде чем приступить к анализу формы и размеров пирамиды Хеопса, следует вспомнить, какой системой мер пользовались египтяне. У египтян было три единицы длины: “локоть” (466 мм), равнявшийся семи “ладоням” (66,5 мм), которая, в свою очередь, равнялась четырем “пальцам” (16,6 мм).

Проведем анализ размеров пирамиды Хеопса (Рис.2), следуя рассуждениям, приведенным в замечательной книге украинского ученого Николая Васютинского “Золотая пропорция” (1990 г.).

Рисунок 2. Геометрическая модель пирамиды Хеопса.

Большинство исследователей сходятся в том, что длина стороны основания пирамиды, например, GF равна L = 233,16 м. Эта величина отвечает почти точно 500 “локтям”. Полное соответствие 500 “локтям” будет, если длину “локтя” считать равной 0,4663 м.

Высота пирамиды (H) оценивается исследователями различно от 146,6 до 148,2 м. И в зависимости от принятой высоты пирамиды изменяются все отношения ее геометрических элементов. В чем причина различий в оценке высоты пирамиды? Дело в том, что, строго говоря, пирамида Хеопса является усеченной. Ее верхняя площадка в наши дни имеет размер примерно 10 ´ 10 м, а столетие назад она была равна 6 ´ 6 м. Очевидно, что вершину пирамиды разобрали, и она не отвечает первоначальной.

Оценивая высоту пирамиды, необходимо учитывать такой физический фактор, как “осадка” конструкции. За длительное время под воздействием колоссального давления (достигающего 500 тонн на 1 м 2 нижней поверхности) высота пирамиды уменьшилась по сравнению с первоначальной высотой.

Какой же была первоначальная высота пирамиды? Эту высоту можно воссоздать, если найти основную “геометрическую идею” пирамиды.

В 1837 г. Английский полковник Г. Вайз измерил угол наклона граней пирамиды: он оказался равным a = 51°51′. Эта величина и сегодня признается большинством исследователей. Указанному значению угла отвечает тангенс (tg a ), равный 1,27306. Эта величина соответствует отношению высоты пирамиды АС к половине ее основания CB (Рис.2), то есть AC / CB = H / (L / 2) = 2H / L.

И вот здесь исследователей ожидал большой сюрприз! Дело в том, что если взять корень квадратный из золотой пропорции , то мы получим следующий результат = 1,272. Сравнивая эту величину с величиной tg a = 1,27306, мы видим, что эти величины очень близки между собой. Если же принять угол a = 51°50′, то есть уменьшить его всего на одну угловую минуту, то величина a станет равной 1,272, то есть совпадет с величиной . Следует отметить, что в 1840 г. Г. Вайз повторил свои измерения и уточнил, что значение угла a =51°50′.

Эти измерения привели исследователей к следующей весьма интересной гипотезе: в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC / CB = = 1,272!

Рассмотрим теперь прямоугольный треугольник ABC, в котором отношение катетов AC / CB = (Рис.2). Если теперь длины сторон прямоугольника ABC обозначить через x, y, z, а также учесть, что отношение y/x = , то в соответствии с теоремой Пифагора, длина z может быть вычислена по формуле:

Если принять x = 1, y = , то

Рисунок 3. “Золотой” прямоугольный треугольник.

Прямоугольный треугольник, в котором стороны относятся как t :: 1, называется “золотым” прямоугольным треугольником.

Тогда, если принять за основу гипотезу о том, что основной “геометрической идеей” пирамиды Хеопса является “золотой” прямоугольный треугольник, то отсюда легко можно вычислить “проектную” высоту пирамиды Хеопса. Она равна:

H = (L/2) ´ = 148,28 м.

Выведем теперь некоторые другие отношения для пирамиды Хеопса, вытекающие из “золотой” гипотезы. В частности найдем отношение внешней площади пирамиды к площади ее основания. Для этого примем длину катета CB за единицу, то есть: CB = 1. Но тогда длина стороны основания пирамиды GF = 2, а площадь основания EFGH будет равна S EFGH = 4.

Вычислим теперь площадь боковой грани пирамиды Хеопса S D . Поскольку высота AB треугольника AEF равна t , то площадь боковой грани будет равна S D = t . Тогда суммарная площадь всех четырех боковых граней пирамиды буде равна 4 t , а отношение суммарной внешней площади пирамиды к площади основания будет равно золотой пропорции! Это и есть – главная геометрическая тайна пирамиды Хеопса!

Анализ других египетских пирамид показывает, что египтяне всегда стремились воплотить в своих пирамидах некоторые важные математические знания. В этом отношении весьма интересной является пирамида Хефрена. Измерения пирамиды показали, что угол наклона боковых граней в ней равен 53°12′, что отвечает отношению катетов прямоугольного треугольника 4:3. Такое отношение катетов соответствует хорошо известному прямоугольному треугольнику со сторонами 3:4:5, который называют “совершенным”, “священным” или “египетским” треугольником. По свидетельству историков, “египетскому” треугольнику придавали магический смысл. Плутарх писал, что египтяне сравнивали природу Вселенной со “священным” треугольником; они символически уподобляли вертикальный катет мужу, основание – жене, а гипотенузу – тому, что рождается от обоих.

Для треугольника 3:4:5 справедливо равенство: 3 2 + 4 2 = 5 2 , которое выражает теорему Пифагора. Не эту ли теорему хотели увековечить египетские жрецы, возводя пирамиду на основе треугольника 3:4:5? Трудно найти более удачный пример для иллюстрации теоремы Пифагора, которая была известна египтянам задолго до ее открытия Пифагором.

Таким образом, гениальные создатели египетских пирамид стремились поразить далеких потомков глубиной своих знаний, и они достигли этого, выбрав в качестве “главной геометрической идеи” для пирамиды Хеопса – “золотой” прямоугольный треугольник, а для пирамиды Хефрена – “священный” или “египетский” треугольник.

Сакральная геометрия Великой Пирамиды Гизы

«Сакральная геометрия» — священная геометрия форм, лежащих в основе жизни. «Геометрия» в переводе с греческого языка означает «измерение земли» .

Пирамида — один из мощнейших символов сакральной геометрии. Египетские пирамиды являют собой удивительный пример геометрической и математической мистики.

Три пирамиды в Гизе располагаются внутри прямоугольника, сформированного из фигурыvesica piscis, которая образуется, когда центры двух кругов с равными радиусами расположены на окружностях друг друга.

Площадь, ограниченная пересекающимися дугами кругов, и есть vesica piscis.

Основополагающей константой в архитектуре, живописи и науке считается Золотое Сечение и именно таковыми являются пропорции Великой Пирамиды Гизы.

Пирамида содержит в себе огромное количество информации о строении Вселенной, Солнечной системы и человека, закодированной в ее геометрической форме, в форме октаэдра, половину которого она представляет.

Пирамиды в Гизе — неразрешимая головоломка из числовых комбинаций. Фотосъемка с воздуха показывает, что пирамиды в Гизе расположены на линии, соответствующей спирали Фибоначчи.

Вершины каждой из трёх Пирамид комплекса в Гизе лежат на спирали Золотого Сечения, или на спирали Фибоначчи, которая при своём раскручивании, приближается к спирали Золотого Сечения.

Древние строители возвели этот величественный монумент с идеальной инженерной точностью и симметричностью.

Это строительное чудо сооружено не на ровной площадке, а на массивном природном холме высотой 9 метров, который занимает 70 процентов основания пирамиды.

Основные характеристики Великой Пирамиды Гизы — пирамиды Хеопса:

• Высота — 138,7 метра, изначальная высота –146,6 м.
• Угол наклона — 51° 50′.
• Длина боковой грани по подсчетам (изначально) — 230,3 м.
• Длина сторон основания пирамиды: юг — 230,45 м, север — 230,25 м, запад — 230,35 м, восток —230,4 м.
• Площадь основания — 5,3 га.
• Периметр – 921,45 метра.
• Средняя масса каменных блоков — 2,5 тонны.
• Самый тяжелый каменный блок — 15 тонн.
• Количество блоков — около 2,5 млн. штук.
• Общий вес пирамиды — около 6,5 млн тонн.
• Широта, на которой находится пирамида — 30°.

Расчеты ученых показывают, что параметры трех главных пирамид и других, находящихся на плато Гизы (проектная высота, углы наклона, периметр, взаимное расположение) связаны друг с другом.

Я на плато Гизы. 20 августа 1996 года

Конструкция Великой Пирамиды основана на пропорции Фи = 1,618. Архитекторы Пирамиды воплотили в камне основополагающие принципы сакральной геометрии:

• Периметр основания пирамиды Хеопса, делённый на удвоенную высоту даёт приближение числа «Пи» — 3,1415…(921,45/2*146,6=3,142).
• Периметр основания пирамиды равен длине окружности, радиус которой равен высоте пирамиды (2*3,14159*146,6=921).
• Длина стороны основания, выраженная в египетских «локтях» (одно из значений — 0,635 м), соответствует продолжительности земного года (230/0,63=365).
• Сумма четырёх сторон пирамиды — 921,45 метра равна половине минуты широты экватора. Один градус широты на экваторе покрывает 110573 м, а каждая дуговая минута — 1842,88 м, что вдвое больше периметра пирамиды.

• Если умножить изначальную высоту Великой Пирамиды – 146,6 м на один миллион, получается наименьшее расстояние от Земли до Солнца —147000000 км (перигелий).
• Соотношение изначальной высоты Великой пирамиды к ее основанию равнялось 7:11. Это соотношение имеет ряд важных геометрических свойств. В нем скрыты числа «Пи» и «Фи».
• Площадь каждой из граней пирамиды равна квадрату ее высоты.
• Длина грани пирамиды, делённая на высоту, даёт соотношение Фи = 1,618.
• Высота в футах — 484,4 соответствует 5813 дюймам(5-8-13) — числа из последовательности Фибоначчи.
• Верхняя северная и нижняя южная шахты построены по диагоналям прямоугольников, описанных вокруг пирамиды.

Если через пирамиду провести две взаимно перпендикулярные плоскости, проходящие через центр, получатся два двойных золотых треугольника, пересечение которых дает крест в квадрате — один из основных эзотерических символов Древнего Египта.

Пирамида является примером подлинной квадратуры круга – задачи, превосходно решённой древними архитекторами, сумевшими построить квадрат, равновеликий кругу.

Круг олицетворяет вечность, Солнце, Ра. Круг вечен, цикличен, но в нём отсутствует направление, любое движение по кругу равносильно отсутствию движения.

Древнеегипетский символ вечности Шен, представляет собой кольцо с перекладиной внизу.

Бог Гор, изображённый в виде сокола, держит в когтях иероглифический знак вечности Шен — символ души Ба.

Квадрат символизирует материю, землю, четыре стороны света и четырех сыновей Гора. Квадрат вводит систему координат, его направления и углы точны и совершенны.

Древние египтяне называли комплекс Гизы – «домом господина Ростау». Это один из титулов бога Осириса. Великую пирамиду они связывали с именем Исиды.

Древнеегипетские легенды гласят, что строителем Великой пирамиды в Гизе был Бог Тот — Атлант — обожествленный царь Египта за десятки тысяч лет до нашей эры. В ней он интегрировал своё знание древней мудрости и спрятал летописи древних Атлантов.

Бесспорно, пирамида Хеопса, как и другие пирамиды Гизы возводились не во времена IV династии, а за многие тысячи лет до фараонов. Их создала древняя, высокоразвитая, высокотехнологичная, возможно, внеземная цивилизация!

[spoiler title=”источники:”]

http://ligis.ru/articles/03/03_25/06/

[/spoiler]