Правильный треугольник. Площадь правильного треугольника
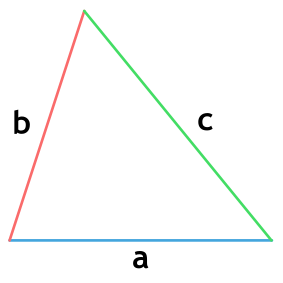
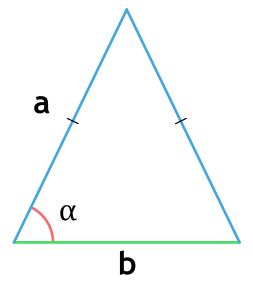
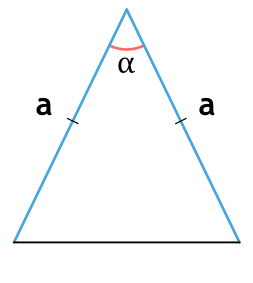
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
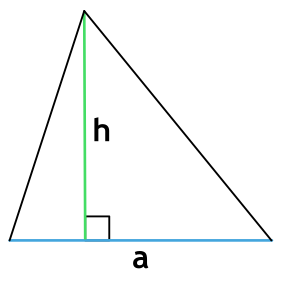
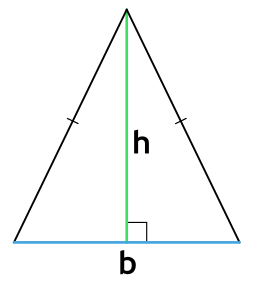
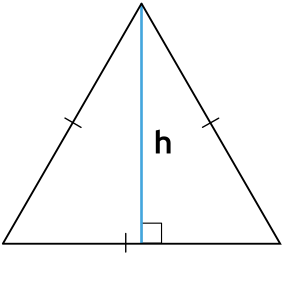
Высота правильного треугольника:
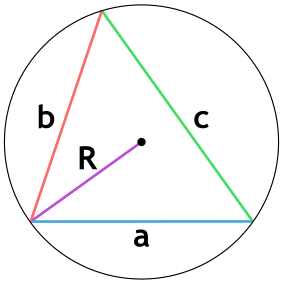
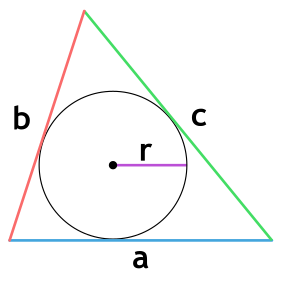
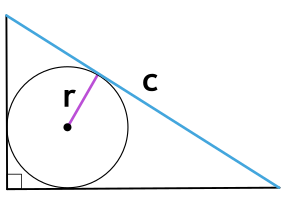
Радиус окружности, вписанной в правильный треугольник:
Радиус описанной окружности в два раза больше:
Площадь правильного треугольника:
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна
. Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна
.
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
Ответ: .
. Сторона правильного треугольника равна
. Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Правильный треугольник. Площадь правильного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Площадь правильного треугольника — формулы, свойства и признаки
Формулы площади
правильного треугольника
- Формула площади правильного треугольника,
выраженная через сторону:
Формула площади правильного треугольника,
выраженная через периметр:
Формула площади правильного треугольника,
выраженная через радиус вписанной окружности:
Формула площади правильного треугольника,
выраженная через радиус описанной окружности:
Мы рассмотрели признаки, того что площадь в треугольнике является
площадью правильного треугольника, и рассмотрели формулы площади
характерные для правильного треугольника.
Признаки площади
правильного треугольника
Площадь в произвольном треугольнике, является площадью
правильного треугольника, если выполняется ряд признаков.
Например, если один из признаков правильного треугольника
истинен для произвольного треугольника, то площадь
можно найти по формулам истинным только для
правильного треугольника.
В правильном треугольнике все углы имеют градусную
меру в 60 градусов.Также, в правильном треугольнике
сумма градусных мер всех углов 180 градусов.
Перечислим основные признаки правильного треугольника:
- Все углы равны.
- Все стороны равны.
- Каждый угол по 60 градусов.
Если, для произвольного треугольника истинен один из
вышеперечисленных признаков, то треугольник правильный.
Соответственно, площадь в правильном треугольнике можно
найти, по формулам площади правильного треугольника.
Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
Площадь правильного треугольника

Средняя оценка: 4.4
Всего получено оценок: 255.
Средняя оценка: 4.4
Всего получено оценок: 255.
Правильные треугольники – это особое явление в геометрии. Все углы треугольника абсолютно точно определены значением в 60 градусов. Из-за этого, помимо обычных для треугольников способов нахождения площади, существуют и способы нахождения именно площади правильного треугольника, не характерные для других фигур. Все способы будут рассмотрены в этой статье.
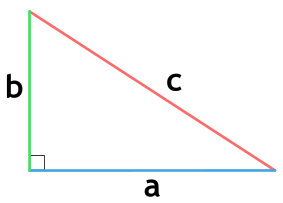
Формулы для нахождения площади треугольника.
- Первая формула площади правильного треугольника стандартна. Площадь равна половине произведения основания на высоту: $S= <1over2>h*a$.
- Существует формула нахождения площади через сторону, которая проистекает из первой, но характерна только для правильных треугольников. В правильном треугольнике АВС проведем высоту АМ, которая будет являться так же медианой и биссектрисой.
Это свойство характерно для равнобедренных треугольников, но любой правильный треугольник и будет равнобедренным, просто любая из его сторон может считаться основанием, так как две другие стороны в любом случае будут равны.
В результате треугольник делиться на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для правильного треугольника.
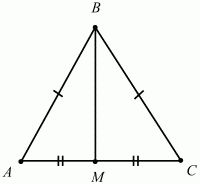
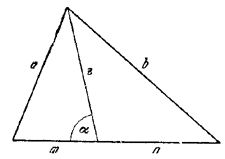
В прямоугольном треугольнике АВМ катет АМ можно выразить через синус угла АВМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет АМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
С другой стороны синус 60 градусов заранее известнее и равен $$sqrt <3>over 2$$ . Значит можно выразить значение АМ:
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
Тогда формула будет выглядеть следующим образом:
Теперь вспомним классическую формулу площади треугольника:
$S= <1over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:
ВС заменили на а, так как все стороны равны между собой, а значение высоты мы находили ранее. Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади полной поверхности через сторону.
По той же причине нельзя использовать эту формулу для равнобедренного или произвольного треугольника. Прежде чем использовать эту формулу необходимо доказать, что треугольник правильный или убедиться, что это условие прописано в исходных данных задачи.
Что мы узнали?
Мы узнали, как можно найти площадь правильного треугольника по стороне, разобрались как эту формулу можно просто и быстро вывести. Запомнив ход вывода можно пользоваться этим в дальнейшем, не запоминая точных значений, а просто проверяя себя, выводя формулу в черновике.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/pravilnyj-treugolnik-i-ego-ploshhad/
http://obrazovaka.ru/geometriya/ploschad-pravilnogo-treugolnika-formula.html
[/spoiler]
Содержание
- Определение правильного треугольника
- Общие сведения
- Особые линии и точки
- Свойства правильных треугольников
- Треугольник с равными сторонами
- Определение равностороннего треугольника
- Длина высоты и ее частей
- Свойства равностороннего треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Пример задачи
- Основные формулы
- Формулы площади
- Через величины a или h
- Через радиусы r или R
- Примеры решения задач
- Описанная и вписанная окружности
- Тетраэдр и его поверхность
Определение правильного треугольника
Треугольник называется правильным, если все его стороны равны: AB + AC + BC. Правильный треугольник еще называется равносторонним.
Общие сведения
Любое пространство можно описать размерностью. В трёхмерном измерении плоская геометрическая фигура, состоящая из трёх отрезков и такого же количества точек, в которых они соединяются, называется треугольником. Отрезки называют сторонами или боковыми гранями, площадь, ограниченная ими — внутренней, а точки — вершинами. Фигура имеет 3 угла и является невырожденной.
Строгого требования к обозначениям элементов многоугольника нет. Но традиционно вершины подписывают заглавными буквами латинского алфавита A, B, C, а противолежащие им стороны — аналогичными строчными знаками. В качестве обозначений для углов используют греческие символы: α, β, γ. Например, если имеется треугольник ABC, у него будут углы A, B, C и стороны a, b, c. Боковые грани могут подписываться и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA.
В зависимости от соотношения размеров сторон, все треугольники разделяют на 3 вида. Они бывают:
- Равнобедренными — многоугольники, у которых одна сторона не равна двум другим. Эта грань называется основанием. Углы при этой стороне равны.
- Разносторонние (неправильные) — длины всех граней разные.
- Равносторонние — треугольники, имеющие одинаковые стороны. Часто эти фигуры называют правильными. По сути, они являются частным случаем равнобедренного многоугольника.
Существуют правила, позволяющие утверждать о равенстве или подобии двух и более треугольников. Они считаются идентичными, то есть их параметры полностью совпадают, если 2 стороны и угол равны или все грани имеют одинаковую длину. А также фигуры будут одинаковыми, когда у них совпадают 2 стороны и угол, располагающийся напротив большего отрезка.
Признаки подобия помогают определить вид треугольника при сравнении с известным. Если 2 любых угла равны в обеих фигурах, они считаются похожими. Когда же 2 стороны многоугольника пропорциональны двум отрезкам другого, причём углы, заключённые между этими гранями, равны, такие фигуры подобны.
Особые линии и точки
Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.
В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.
Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:
- Отрезок BH перпендикулярен прямой AC по построению.
- Точка H разделяет отрезок AC на AD и CD. Если это утверждение будет верным, это означает, что построенная высота BH будет медианой треугольника.
- Отрезок BH создаёт в многоугольнике 2 угла — ∠ABH и ∠CBH. При верности этого утверждения можно утверждать, что отрезок BH является биссектрисой.
Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.
Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.
Точка, в которой пересекаются отрезки, будет центром тяжести фигуры. Её особенность в том, что она разделяет эту линию на 2 части в отношении 2 к 1, если считать от угла. Кроме этого, из-за равенства медианы и биссектрисы эта точка будет и ортоцентром.
Свойства правильных треугольников
- В правильном треугольнике все углы равны между собой и равны 60^.
- Высота в равностороннем треугольнике совпадает с медианой и биссектрисой.
- Центры пересечения медиан, биссектрис и высот совпадают.
- Центры вписанной и описанной окружностей совпадают.
- Радиусы r и R, вписанной и описанной окружностей равностороннего треугольника, связаны с длиной его стороны a следующими соотношениями:r=frac{sqrt{3}}{6} a, quad R=frac{sqrt{3}}{3} a$$
Треугольник с равными сторонами
Каждый школьник, в каком бы классе он ни учился, знает, что собой представляет треугольник. Он является самой простой замкнутой фигурой на плоскости и в пространстве, поскольку образован тремя отрезками (четырьмя ограничены следующие по сложности за ним фигуры: прямоугольник, квадрат, параллелограмм и т. д. ).
Состоит он из трех сторон, которые определяют 3 его угла (отсюда и название геометрического объекта). Для определения значений углов в градусах следует при решении задач использовать теорему о равенстве их суммы — 180. При этом неважно, к какому типу относится сама фигура (равнобедренный, прямоугольный и т. д. ), теорема остается справедливой всегда.
Исходя из названия, равносторонний треугольник — плоская фигура, все 3 стороны которой равны между собой. Для нее являются справедливыми следующие свойства:
- Все 3 угла равны между собой и составляют 60 градусов, поэтому его также называют равноугольным. Это утверждение справедливо в обратную сторону: если все углы треугольника составляют 60 градусов, он является равносторонним.
- Медиана, биссектриса и высота совпадают друг с другом, то есть любая из этих линий будет делить угол пополам, противоположную сторону на 2 равные части и будет перпендикулярна ей одновременно.
- Наличие трех осей симметрии. Все они совпадают с соответствующими медианами, биссектрисами, высотами. Оси пересекаются в точке, которая является геометрическим и массовым центром фигуры. Повороты на 0, 120, 240 и 360 градусов вокруг этой точки треугольника будут переводить его самого в себя, то есть являются операциями симметрии.
- Любые 2 рассматриваемых треугольника являются подобными. Этот вывод следует из равенства их трех углов.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Длина высоты и ее частей
Прежде чем приводить формулы площади равностороннего треугольника, следует выяснить, какую длину имеют его биссектрисы, высоты или медианы. Пусть эта величина будет обозначаться латинской буквой h, а сторона фигуры обозначается a. Поскольку проведенная высота из любого угла делит его на 2 прямоугольных треугольника, этот факт можно использовать для вычисления величины h. Проще всего применить определение какой-либо тригонометрической функции, например, синуса:
sin (60) = h/a.
Согласно определению, синусом угла называется отношения противолежащего катета (h) к гипотенузе (a). Поскольку значения функции sin (60) является табличной величиной, получается следующее выражение для h:
h = 30,5 /2*a.
Из формулы следует, что высота h составляет приблизительно 87% от длины стороны a.
Для получения полной информации о свойствах биссектрис, медиан и высот треугольника, нужно определить, на какие части делит их точка пересечения. Следует ввести некоторые обозначения:
- A, B, C — вершины равноугольного треугольника;
- Q — точка пересечения биссектрис, медиан и высот фигуры;
- P — середины стороны BC, на которую опущена высота AP.
Треугольник PQB является прямоугольным. Прямым углом будет QPB. Поскольку угол QBP разделен биссектрисой на 2 одинаковые части, он составляет 30 градусов. Катет QP лежит против этого угла, поэтому будет иметь длину в 2 раза меньшую, чем гипотенуза BQ. Нетрудно увидеть, что сумма длин BQ и QP равна высоте h. Эти рассуждения позволяют получить следующие формулы:
- QP = ½*BQ = 1/3*h = 30,5 /6*a = r;
- BQ = 2*QP = 2/3*h = 30,5 /3*a = R.
Здесь введены новые буквы r и R для обозначения длин QP и BQ, соответственно.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
- CD перпендикулярна AB => ∠ADC = ∠BDC = 90°
- AD = DB
- ∠ACD = ∠DCB = 30°
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Основные формулы
Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √3) / 2.
Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √((2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √(2a — a) / (2a + a) = (a / 2) * √(1 / 3) = a / (2 * √3) = (a √3) / 6.
Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB2 = h2 + (AB / 2)2. Это равенство решают следующим образом: AB2 = h2 + AB2 / 22. Выражение можно преобразовать в вид: (3a2 / 4) = h 2 → a 2 = (4 * h2) / 3 → a 2 = √((4 * h2) / 3) → a = (2 * h) / √3.
Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:
- Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a2 * sin 60 = ½ * a2 * √3 / 2 = (√3 / 4) * a2. Что и следовало доказать.
- Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.
Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a2 = b2 + c2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.
Формулы площади
Чему равна площадь равностороннего треугольника можно определить с использованием нескольких формул. Для этого привлекаются в том числе понятия вписанной и описанной окружности.
Через величины a или h
Площадь абсолютно любого треугольника может быть определена как произведение его высоты на длину основания, которое следует поделить пополам. Если записать это выражение для равноугольного треугольника, можно получить следующие формулы:
- S = ½*a*h;
- S = 30,5 /4*a 2 ;
- S = 30,5 /3*h 2 .
Для получения этих выражений была использована формула связи между длинами высоты h и основания a. Уравнения справедливы для любого треугольника с равными сторонами. Для прямоугольного или равнобедренного эти выражения уже не подходят.
Формулы через длины h и a для площади S говорят, что для однозначного определения геометрической характеристики достаточно знать лишь один параметр треугольника, имеющий размерность длины.
Через радиусы r или R
Чтобы определить площадь, достаточно узнать любой линейный параметр. Это необязательно может быть сторона или высота, но также радиусы вписанной и описанной окружностей.
Вписанной называется окружность, которая лежит внутри фигуры и касается всех ее сторон. В случае равностороннего треугольника ее центр находится в точке пересечения медиан (высот, биссектрис), то есть в точке Q. Ее радиус r равен отрезку QP и составляет:
r = 30,5 /6*a.
Выразив из этого равенства сторону a и подставив ее в формулу для площади S через a, можно получить следующее выражение:
S = 3*30,5 *r 2 .
Центр вписанной окружности является для равностороннего треугольника центром описанной вокруг него. Ею принято называть в геометрии фигуру, которая проходит через все вершины многоугольника. Поскольку ее центр лежит в точке Q, радиус R будет равен длине отрезка QB. Формула для него уже известна:
R = 30,5 /3*a.
Аналогичным образом, выражая из этого равенства величину a, и подставляя ее в формулу для S, можно получить следующее выражение:
S = 3*30,5/4*R 2 .
Это равенство можно было также получить, если вспомнить, что радиус описанной окружности R в 2 раза больше радиуса r.
Примеры решения задач
Выведенные формулы можно с легкостью применять для решения разнообразных задач по геометрии. Для понимания, как их следует использовать, следует рассмотреть несколько примеров.
Чтобы уметь решать различные задания, связанные с треугольником, нужно помнить всего несколько формул. Но понадобится знать, что углы в фигуре равны друг другу и составляют 60 градусов. Часто придётся применять и теорему Пифагора. Вот некоторые из типовых заданий, используемые при обучении школьников в седьмом классе:
- Какой будет радиус вписанной в правильный треугольник окружности, если его высота равняется 9 см. Зная свойство фигуры, решить задачу можно за пару секунд. Так как радиус равен 1/3 высоты, ответом на задачу будет: r = h / 3 = 9 / 3 = 3 см.
- Сторона равностороннего треугольника равняется корню из трёх. Определить диаметр описанной окружности. Известно, что отношение синуса к противолежащему углу составляет 2R. Следовательно: R = a / 2 * sin (a) = √3 * 2 / 2 * √3 = 1.
- Вокруг треугольной фигуры со стороной 8 √3 описан круг. Узнать его радиус. Эта задача в 2 действия. Используя формулу для нахождения вписанного радиуса и определение r = R / 2 можно записать: R = 2 * a * √3 / 6 = 2 * 8 * √3 * √3 / 6 = 2 * 4 = 8.
- Пусть имеется квадрат, вокруг которого описана окружность. В ней так же располагается правильный треугольник. Периметр треугольной фигуры равен 9 √ 6. Нужно вычислить сумму всех сторон квадрата. На первом шаге необходимо определить длину боковой грани треугольника. Найти её можно по формуле: a = 3 √6. Теперь возможно рассчитать радиус описанной окружности: a = R * √3. Выполнив подстановку, найти ответ несложно: R = 3 √6 / √3 = 3 * √2. На третьем шаге можно выяснить, чему равняется сторона четырёхугольника. В этом поможет равенство: 3 √2 = (n √2) / 2. Отсюда n = 6. Значит, периметр квадрата равняется: P = 4 * 6 = 24.
Проверить правильность решения, возможно, используя онлайн-калькуляторы. Это сервисы, которые предлагают бесплатно вычислить элементы правильной фигуры. При этом от пользователя требуется лишь внести в специальную форму исходные данные и нажать кнопку «Рассчитать».
Следует отметить, что выучить наизусть все формулы сложно, поэтому обычно используют логическое мышление и теоремы синусов-косинусов. Учитывая, что любой угол в равностороннем треугольнике равен 60 градусов практически любую формулу вывести можно самостоятельно.
Описанная и вписанная окружности
Дан некоторый равноугольный треугольник. Известно, что разница между радиусами описанной и вписанной окружностей составляет 3 см. Следует найти площадь фигуры.
На первый взгляд может показаться, что нахождение решения этой задачи требует проведения некоторых промежуточных вычислений, но это не так. Если вспомнить, что радиус описанной окружности R ровно в 2 раза больше величины r, то их разница является не чем иным, как самим радиусом вписанной окружности r. Для получения ответа на задачу следует всего-навсего воспользоваться известной формулой и вычислить S:
S = 3*30,5 *r 2 = 46,765 см 2 .
Тетраэдр и его поверхность
Тетраэдр является объемной фигурой, которая ограничена четырьмя гранями, являющимися равноугольными треугольниками. Необходимо определить площадь поверхности этой геометрической фигуры, если известно, что ее объем составляет 100 см 3 .
Чтобы посчитать необходимую площадь, следует найти эту величину всего лишь для одного равностороннего треугольника, а затем полученное число умножить на 4. Из курса стереометрии известно, что объем тетраэдра рассчитывается по следующей формуле:
V = 20,5 /12*a 3 .
Отсюда можно получить длину стороны a:
a = (12*V/20,5)^(1/3).
Подставляя значение объема тетраэдра из условия задачи, можно рассчитать a = 9,467 см. Это значение округлено до третьего знака после запятой.
Теперь можно применить формулу для расчета площади S через a:
S = 30,5/4*a 2 = 38,81 см 2 .
Получилась площадь одной грани тетраэдра. Поскольку объемная фигура состоит из четырех одинаковых треугольников, то площадь его поверхности St составит:
St = 4*S = 155,24 см 2 .
Таким образом, высокая симметрия равностороннего треугольника позволяет рассчитывать его площадь, зная всего один линейный параметр фигуры. Чаще всего таковым является высота, сторона основания или радиусы вписанной и описанной окружностей.

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
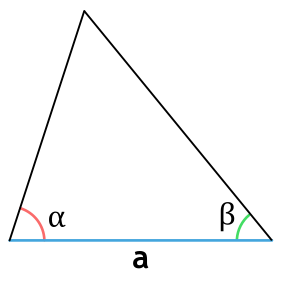
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты
{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность
{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону
{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности
{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности
{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
- 2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
1. Через длину основания (a) и высоту (h):
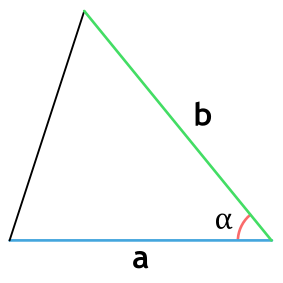
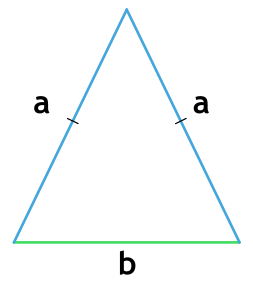
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник