Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба


r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними
 ,
,
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба


где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними
 ,
,
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны


где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними


φ – любой из четырёх углов между ними
Квадрат

где
a – сторона квадрата




Получается из верхней формулы подстановкой d = 2R
Ромб

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба





где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция


где
a и b – основания,
h – высота



φ – любой из четырёх углов между ними



где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними


где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


Произвольный выпуклый четырёхугольник


φ – любой из четырёх углов между ними
Вписанный четырёхугольник




где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле


Доказательство . В соответствии с рисунком 1 справедливо равенство:




что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
 ,
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).



что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
 ,
,
где a и b – основания трапеции, а h – высота высота высота (рис.5).


Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому


что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):






 ,
,
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба
a – сторона куба
Формула площади поверхности куба,(S):
2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
3. Найти площадь поверхности шара, сферы
R – радиус сферы
Формула площади поверхности шара (S):
4. Найти площадь боковой и полной поверхности цилиндра
r – радиус основания
h – высота цилиндра
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
5. Площадь поверхности прямого, кругового конуса
R – радиус основания конуса
H – высота
L – образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | диагональ и угол между ними | ||
| 2 | стороны и углы между этими сторонами | ||
| 3 | стороны (по Формуле Брахмагупты) |
||
| 4 | стороны и радиус вписанной окружности | ||
| 5 | стороны и углы между ними |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-24-00-29-48
http://doza.pro/art/math/geometry/area-tetragon
[/spoiler]
Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба

a – сторона куба
Формула площади поверхности куба,(S):
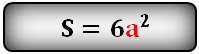
2. Найти площадь поверхности прямоугольного параллелепипеда

a, b, c – стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):

3. Найти площадь поверхности шара, сферы

R – радиус сферы
π ≈ 3.14
Формула площади поверхности шара (S):
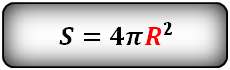
4. Найти площадь боковой и полной поверхности цилиндра
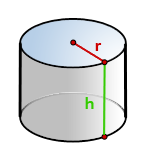
r – радиус основания
h – высота цилиндра
π ≈ 3.14
Формула площади боковой поверхности цилиндра, (Sбок):
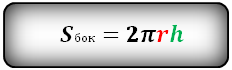
Формула площади всей поверхности цилиндра, (S):

5. Площадь поверхности прямого, кругового конуса
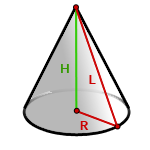
R – радиус основания конуса
H – высота
L – образующая конуса
π ≈ 3.14
Формула площади боковой поверхности конуса, через радиус (R) и образующую (L), (Sбок):

Формула площади боковой поверхности конуса, через радиус (R) и высоту (H), (Sбок):

Формула площади полной поверхности конуса, через радиус (R) и образующую (L), (S):

Формула площади полной поверхности конуса, через радиус (R) и высоту (H), (S):

6. Формулы площади поверхности усеченного конуса
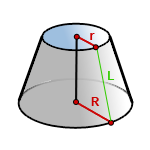
R – радиус нижнего основания
r – радиус верхнего основания
L – образующая усеченного конуса
π ≈ 3.14
Формула площади боковой поверхности усеченного конуса, (Sбок):

Формула площади полной поверхности усеченного конуса, (S):
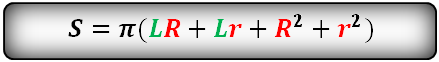
7. Площадь поверхности правильной пирамиды через апофему
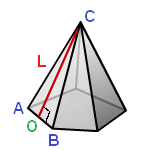
L – апофема (опущенный перпендикуляр OC из вершины С, на ребро основания АВ)
P – периметр основания
Sосн – площадь основания
Формула площади боковой поверхности правильной пирамиды (Sбок):
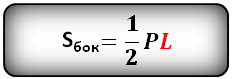
Формула площади полной поверхности правильной пирамиды (S):
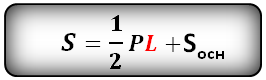
8. Площадь боковой поверхности правильной усеченной пирамиды
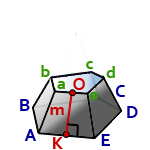
m – апофема пирамиды, отрезок OK
P – периметр нижнего основания, ABCDE
p – периметр верхнего основания, abcde
Формула площади боковой поверхности правильной усеченной пирамиды, (S):
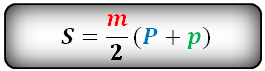
9. Площадь поверхности шарового сегмента

R – радиус самого шара
h – высота сегмента
π ≈ 3.14
Формула площади поверхности шарового сегмента, (S):

10. Площадь поверхности шарового слоя
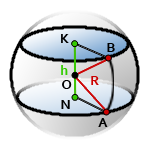
h – высота шарового слоя, отрезок KN
R – радиус самого шара
O – центр шара
π ≈ 3.14
Формула площади боковой поверхности шарового слоя, (S):

11. Площадь поверхности шарового сектора
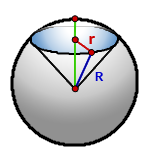
R – радиус шара
r – радиус основания конуса = радиус сегмента
π ≈ 3.14
Формула площади поверхности шарового сектора, (S):

 В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).
В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).
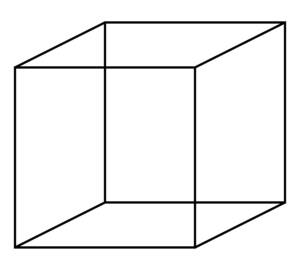
Как выглядит призма
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.
Рисунок, на котором изображена четырёхугольная призма, показан ниже.
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:
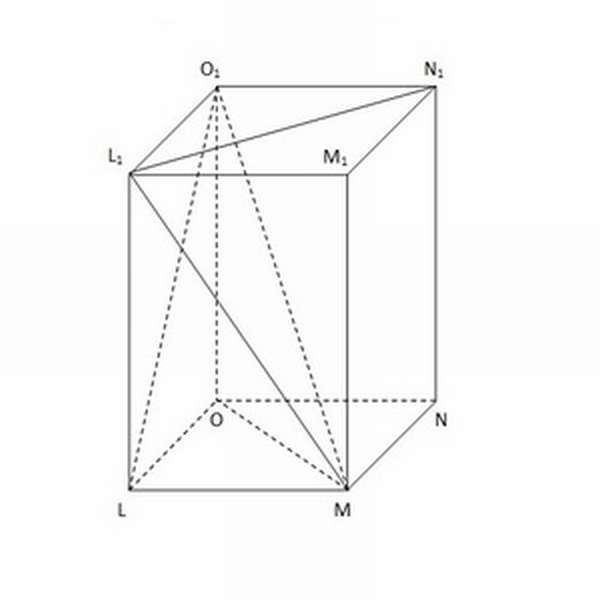 Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
Основы призмы — квадраты LMNO и L₁M₁N₁O₁.- Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
- Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
- Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).
Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.
Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).
Площадь поверхности и объём
Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:
V = Sосн·h
Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:
V = a²·h
Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:
V = a³
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.
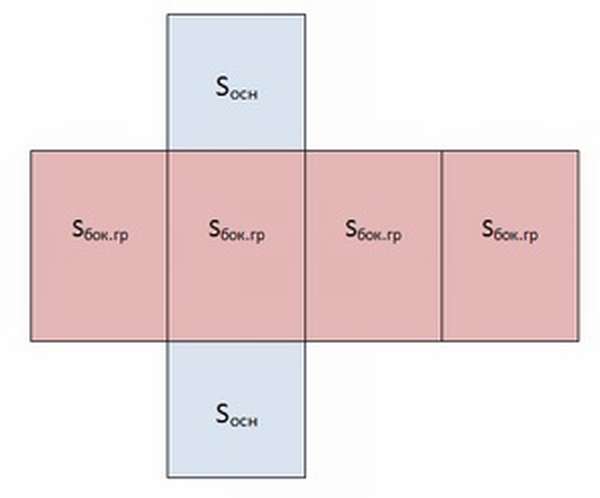
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:
Sбок = Pосн·h
С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:
Sбок = 4a·h
Для куба:
Sбок = 4a²
Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:
Sполн = Sбок + 2Sосн
Применительно к четырёхугольной правильной призме формула имеет вид:
Sполн = 4a·h + 2a²
Для площади поверхности куба:
Sполн = 6a²
Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.
Нахождение элементов призмы
Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:
- длина стороны основания: a = Sбок / 4h = √(V / h),
- длина высоты или бокового ребра: h = Sбок / 4a = V / a²,
- площадь основания: Sосн = V / h,
- площадь боковой грани: Sбок. гр = Sбок / 4.
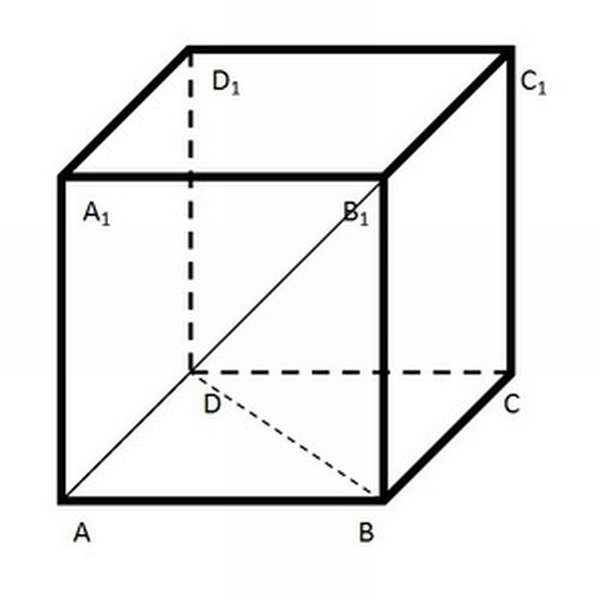 Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:
Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:
Sдиаг = ah√2
Для вычисления диагонали призмы используется формула:
dприз = √(2a² + h²)
Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.
Примеры задач с решениями
Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.
В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?
Решение.
Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:
V₁ = ha² = 10a²
Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:
V₂ = h (2a)² = 4ha²
Поскольку V₁ = V₂, можно приравнять выражения:
10a² = 4ha²
После сокращения обеих частей уравнения на a² получается:
10 = 4h
В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.
ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.
Решение.
Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.
Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.
Длина любого ребра определяется через известную диагональ:
a = d / √2 = 6√2 / √2 = 6
Площадь полной поверхности находится по формуле для куба:
Sполн = 6a² = 6·6² = 216

Задание 3.
В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?
Решение.
Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.
Длина комнаты составляет a = √9 = 3 м.
Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².
Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.
Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.
Как найти площадь куба









Проститутки Ростов на Дону rostovchanotki.ru
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
- 2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы

Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:![]()
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:![]()
Определение четырехугольника
Четырехугольник – это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.
Свойства четырехугольников
Четырехугольник может быть:
- Самопересекающимся
- Невыпуклым
- Выпуклым

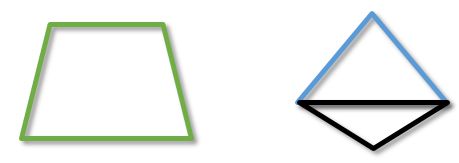
Самопересекающийся четырехугольник – это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).
Невыпуклый четырехугольник – это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен красным цветом)
Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.
Особые виды четырехугольников
Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:
- Параллелограмм
- Ромб
- Прямоугольник
- Квадрат
- Трапеция
- Дельтоид
- Контрпараллелограмм
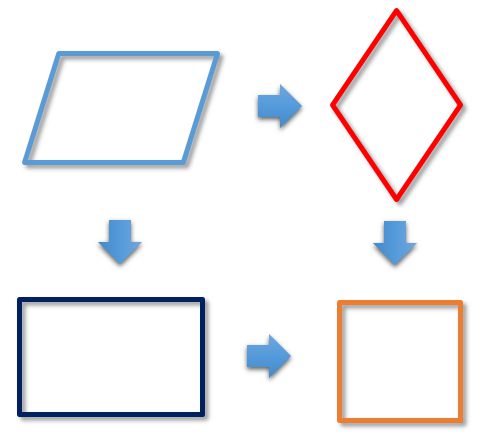
Подробнее о каждом из особых видов четырехугольника можно узнать, перейдя по ссылкам выше.
Как видно из рисунка, особые виды четырехугольников наследуют свойства своих “предков”. Например, прямоугольник (на рисунке показан темно-синим цветом) является особым случаем параллелограмма (на рисунке показан голубым цветом). Таким образом, у него сохраняются все его свойства и добавляются свои, особенные. Поэтому при решении задач про прямоугольники можно применять все свойства и теоремы параллелограмма.
Квадрат (на рисунке показан оранжевым цветом) – частный случай прямоугольника. То есть квадрат имеет все свойства параллелограмма, прямоугольника, а также и свои, особенные. Но, самое интересное, квадрат также является частным случаем ромба (на рисунке показан красным цветом), то есть, кроме указанных (параллелограмм, прямоугольник), он обладает еще и всеми свойствами ромба.
Также, интересными особыми случаями четырехугольника являются трапеция и дельтоид.
Четырехугольник и окружность
Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).
Главное свойство описанного четырехугольника:
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.
Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)
Главное свойство вписанного четырехугольника:
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.
Свойства длин сторон четырехугольника
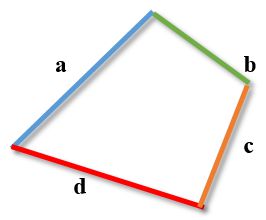
Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.
|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b
Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.
В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.
a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c
Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (<). Равенство достигается только в случае, если четырехугольник является “вырожденным”, то есть три его точки лежат на одной прямой. То есть эта ситуация не попадает под классическое определение четырехугольника.
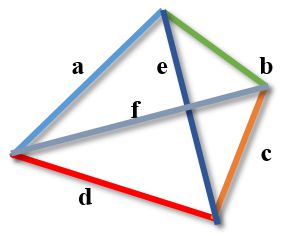
Соотношение сторон и диагоналей может быть выражено формулой
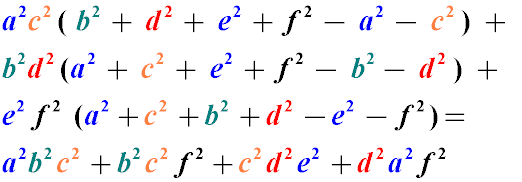
Неравенство Птолемея
![]()
Произведение длин диагоналей четырехугольника меньше или равно сумме произведений противоположных сторон четырехугольника.
Теорема Гаусса
Если в четырёхугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего две точки пересечения диагоналей и точку пересечения этих двух пар противоположных сторон.
Соотношение Бретшнайдера
Произведение квадратов диагоналей произвольного несамопересекающегося четырехугольника равно сумме произведений квадратов его противоположных сторон минус удвоенное произведение всех его сторон, которое умножено на косинус суммы двух противоположных углов.
![]()
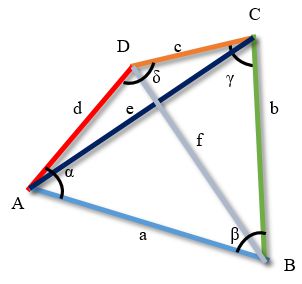
Формула Эйлера
Квадрат двойного расстояния между серединами диагоналей произвольного несамопересекающегося четырехугольника равен сумме квадратов его сторон минус сумма квадратов его диагоналей
![]()
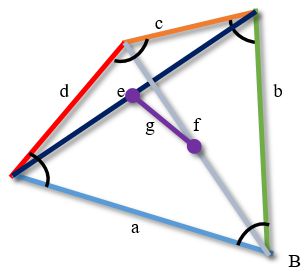
Средние линии четырехугольника
У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями.
Центроид четырехугольника
Центроидом четырехугольника называется точка пересечения всех его средних линий.
Обобщенная теорема Ньютона
Средние линии несамопересекающегося четырехугольника, образуемые серединами противолежащих сторон (первая и вторая средняя линия) и отрезком, соединяющим середины диагоналей (третья средняя линия) пересекаются в одной точке и делятся ею пополам.
Прямая, проходящая через середины диагоналей четырехугольника и его центроид также называется прямой Ньютона.
(см. рисунок выше)
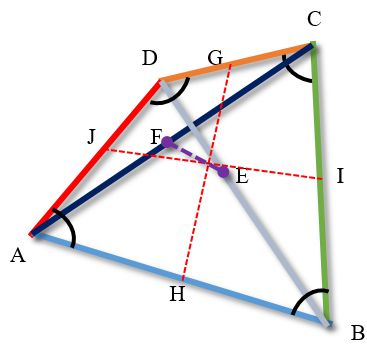
Теорема Вариньона
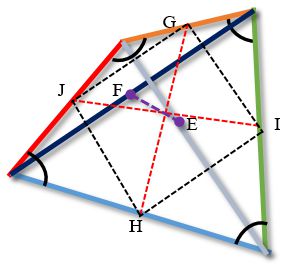
Четырёхугольники, которые образуются отрезками, соединяющими середины противолежащих сторон (GIHJ), а также середины диагоналей четырехугольника и середины противолежащих сторон (EHFG, JEIF) являются параллелограммами.
Эти параллелограммы называются параллелограммами Вариньона.
Четырехугольник, образованный серединами противолежащих сторон (на рисунке обозначен пунктирной линией GIHJ) называется большим параллелограммом Вариньона.
- Центры всех трёх параллелограммов Вариньона лежат на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
- Периметр большого параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
- Площадь большого параллелограмма Вариньона равна половине площади исходного четырёхугольника
- Площадь исходного четырёхугольника равна произведению первой и второй средних линий четырёхугольника на синус угла между ними
- Сумма квадратов трёх средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей
0
Вписанная в треугольник окружность |
Описание курса
| Существование четырехугольника
