Эту задачу я нашел на канале MathBrain. Дал своим ученикам, двое решили за минуту, остальные думали дольше, но решили все.
Задача чисто геометрическая – надо найти площадь большого квадрата, если известна площадь маленького красного треугольника.
Не устаю говорить, что геометрические задачи хороши тем, что они отлично развивают пространственное мышление и логику, умение находить разные способы решения и решать не по алгоритму, как в алгебре и во многих других дисциплинах. Так что, если не хотите, чтобы или ваше дети были полуроботами, которые могут работать только по алгоритму [а ещё говорят, что такими людьми легко управлять], решайте геометрические задачки.
Тут есть два способа решения. Один строгий, через уравнения, как многие любят. Другой красивый, вообще без формул.
Начну с первого, строгого. Для этого давайте обозначим половину стороны большого квадрата за Y, а катет красного треугольника за X. Надеюсь, что никому не нужно доказывать, что треугольник красный треугольник прямоугольный?! На всякий случай вот поясняющий рисунок.
Рассматриваем левый верхний треугольник: у него два катета равны Y, а гипотенуза 2X. По теореме Пифагора (2Х)²=2Y²; 4Х²=2Y²; 2Х²=Y².
Площадь большого квадрата можно записать как 4Y²=8X². Осталось найти Х. Это легко сделать с помощью красного треугольника с известной площадью. S=½X²=1 следовательно X²=2. подставляем в площадь большого квадрата и получаем 8X²=8·2=16.
***
Теперь второй способ. Дорисуем диагонали большого квадрата. Таким образом он поделится на 16 равных прямоугольных треугольников равных красному. Стало быть площадь большого квадрата – это 16 площадей красного треугольника, то есть 16.
Какое решение вам больше понравилось? И как решили вы?
Ещё интересно: Математики всего мира не могут договориться, о том, какой ответ считать правильным: 9 или 1
Олимпиадная задача для 8 класса, которая решается устно
Сосед Серёга в очередной раз сложил из спичек какую-то композицию – три разных квадрата лежат на отрезке AJ. Сторона самого маленького меньше стороны среднего на две спички. А сторона самого большого больше, наоборот, больше на три. При этом в упомянутый отрезок AJ аккуратно ложатся 16 спичек.
Задача: Чему равна площадь самого большого квадрата GHIJ?
P.S. Короткие ответы лучше несите мимо.
Начнем с того, что, пусть сторона среднего квадрата будет – Х.
Тогда сторона самого маленького квадрата будет – Х-2;
А сторона самого большого квадрата будет – Х+3;
Воспользуясь этими данными составим вот такое уравнение:
Х+(Х-2)+(Х+3)=16;
3Х=16+2-3;
3Х=15
Х=5;
Значит сторона среднего квадрата равна 5 спичкам.
Теперь нам нужно найти сторону самого большого квадрата. А она больше на три спички стороны среднего квадрата: 5+3=8;Получается, сторона самого большого квадрата равна 8 спичкам.
Если сторона самого большого квадрата GHIJ равна 8 спичкам, то его площадь будет равна 8*8=64 квадратным спичкам.
Ответ: 64 квадратные спички.
автор вопроса выбрал этот ответ лучшим
Алеся Ясногорцева
[73.7K]
более месяца назад
Единица измерения здесь, насколько я поняла – одна спичка. Сторону самого маленького квадрата выражаем через х, сторону среднего – через х + 2, сторону самого большого – через х + 5 (если самый большой квадрат больше среднего на 3 спички, а средний больше самого маленького на 2 спички, то самый большой больше самого маленького на 5 спичек).
Составляем уравнение:
х + (х + 2) + (х + 5) = 16
3х + 7 = 16
3х = 16 – 7
3х = 9
х = 9/3
х = 3.
Итак, самый маленький квадрат имеет сторону размером в 3 спички. А длина самого большого квадрата – соответственно, 3 + 5 = 8. Если сторона большого квадрата равна 8 спичкам, то в площадь его уместятся 8 * 8 = 64 квадратиков, сделанных из одной спички.
Сколько это в сантиметрах, мы не знаем,, но предположить можно. Длина стандартной спички – максимум,, 5 см. 8 * 5 = 40 (длина стороны самого большого квадрата. 40 * 40 = 1600 см в квадрате.(площадь его)
Росинка Роса
[477K]
более месяца назад
Для решения данной задачи обозначим сторону самого малого квадрата символом Х
Тогда сторона среднего квадрата будет по условию Х + 2
И сторону третьего, наибольшего квадрата, можем выразить через Х, это примет вид: (Х + 2) + 3
Сумма всех сторон данных квадратов известна , это 16.
Можем составить уравнение
Х + (Х + 2) + Х +2 + 3 = 16
Скобки чисто для наглядности, они не нужны вообще-то.
Упростим уравнение.
Х + Х + 2 + Х + 2 + 3 = 16
Решим уравнение
3Х + 7 = 16
3Х = 16 – 7 = 9
3Х = 9
Х = 3
Следовательно стороны квадратов будут:
3
3 + 2 = 5
5 + 3 = 8
Площадь самого большого квадрата 8*8 = 64 (условных единиц квадратных)
Nasos
[171K]
более месяца назад
В отрезок AJ по условию задачи укладывается:
- сторона маленького квадрата ABCD
- сторона маленького квадрата плюс две спички
- сторона маленького квадрата ABCD плюс две спички и ещё плюс три спички
Таким образом в сумме это будет три стороны маленького квадрата ABCD и плюс семь спичек.
Поскольку это по условию равно 16-ти спичкам, то отсюда следует, что сторона маленького квадрата ABCD составлена из трёх спичек.
Тогда сторона самого большого квадрата GHIJ будет составлять сторону маленького квадрата ABCD плюс пять спичек, итого восемь спичек.
А вот площадь большого квадрата GHIJ будет тогда равна 64-м квадратным спичкам.
Знаете ответ?
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь квадрата
Площадь квадрата равна квадрату его стороны.
Доказательство
Дано: квадрат,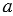 
– сторона квадрата, 
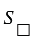– площадь квадрата.
Доказать: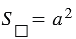 
.
Доказательство:
1 случай
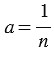, где 
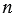– целое число. Возьмем квадрат со стороной 1, разобьем его на 
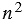равных квадратов (на рисунке 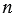= 5).
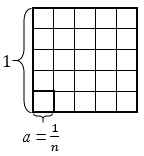
Площадь большого квадрата равна 1, следовательно, чтобы найти площадь каждого маленького квадратика, нужно площадь большого квадрата разделить на количество маленьких квадратиков, число которых 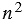, т.е. получим 
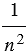– площадь каждого маленького квадратика. Сторона каждого маленького квадрата равна 
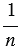, значит, равна 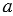, т.к. 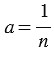. Получаем
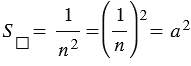. (1)
2 случай
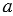– конечная десятичная дробь, содержащая 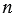знаков после запятой (если 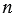= 0, то 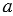– целое число), 
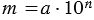– целое число. Разобьем данный квадрат со стороной 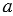на 
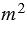равных квадратов (на рисунке 
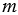= 7).
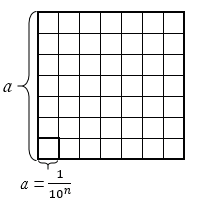
Каждая сторона данного квадрата разобьется на 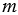равных частей, тогда сторона любого маленького квадрата равна 
.
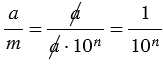По формуле (1) площадь маленького квадрата равна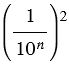 
, чтобы найти площадь данного квадрата, нужно умножить число маленьких квадратов на их площадь, т.е.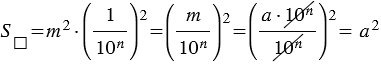 
.
3 случай
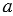– бесконечная десятичная дробь. Рассмотрим число 
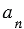, получаемое из 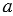отбрасыванием всех десятичных знаков после запятой, начиная с 
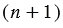– го. Так как число 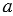отличается от числа 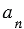не более чем на 
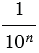, то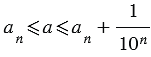 
, откуда
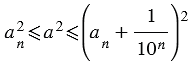. (2)
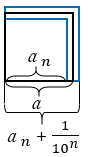
Площадь 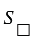данного квадрата заключена между площадью квадрата со стороной 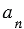и площадью квадрата со стороной 
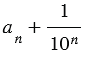(смотри рисунок ниже),
т.е. между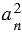 
и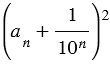 
, значит:
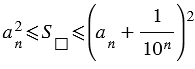. (3)
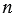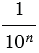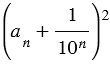Если неограниченно увеличивать число , то число будет становиться сколь угодно малым, число будет сколь угодно мало отличаться от числа 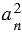. Поэтому из неравенств (2) и (3) следует, что число сколь угодно мало отличается от числа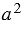 
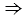
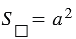, . Что и требовалось доказать.
Советуем посмотреть:
Понятие площади многоугольника
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 449,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 456,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 457,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 458,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 506,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1087,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1123,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1128,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1136,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1211,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Площадь квадрата онлайн
С помощю этого онлайн калькулятора можно найти площадь квадрата. Для нахождения площади квадрата, введите известные данные в ячейку и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Площадь квадрата. Определение
Определение 1. Площадь квадрата − это величина той части плоскости, которую занимает квадрат.
Единицы измерения площади квадрата
За единицу измерения площадей применяют квадрат, сторона которого равна единице измерения отрезков. В качестве единицы измерения площадей принимают квадраты со сторонами 1мм, 1см, 1дм, 1м и т.д (Рис.1). Такие квадраты назыают квадратным миллиметром, квадратным сантиметром, квадратным дециметром, квадратным метром и т.д., соответственно. Обозначаются они мм2, см2, дм2, м2 и т.д., соответственно.
Если выбрана единица измерения, то площадь измеряемого объекта (квадрата, треугольника, прямоугольника, многоугольника и т.д.)определяется положительным числом, которая определяет сколько раз единица измерения и ее части укладываются в данном объекте.
Для измерения отдельных плоских фигур используются специальные формулы. В данной статье мы выведем формулу для вычисления площади квадрата.
Площадь квадрата. Доказательство
Теорема 1. Площадь S квадрата со стороной a равна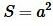 
.
Доказательство. Пусть n целое неотрицательное число и пусть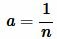 
. Рассмотрим квадрат со стороной 1 (Рис.2). Разделим этот квадрат по ветрикали и по горизонлали на n равных частей. Получим 
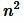маленьких квадратов состоронами 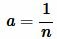. Поскольку площадь большого квадрата равна 1 (так как является единицей измерения), то очевидно, что площадь маленького квадрата равна:
а поскольку 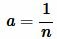, то имеем:
Пусть теперь a является конечной десятичной дробью, содержащую n знаков после запятой. (Если n=0, то a будет целым числом). Тогда a можно представить в виде обыкновенной дроби, умножив и делив на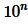 
:
откуда
где m − целое число.
Возьмем квадрат со стороной a и разделим его по горизонлали и вертикали на m ровных частей. Получим m2 маленьких квадратов (Рис.3).
Тогда, учитывая (2), сторона каждого квадрата равна:
По формуле (1) площадь маленького квадрата равна:
Следовательно, площадь квадрата со стороной a равна:
Пусть, далее, число a представляет собой бесконечную десятичную дробь. Рассмотрим число an которая получается из a отбрасыванием всех десятичных знаков после запятой, начиная с (n+1)-го. Поскольку a отличается от an не более, чем на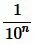 
, то имеем:
откуда
Из неравенства (4) следует, что площадь S квадрата со стороной a заключена между площадью квадрата со стороной an и площадью квадрата со стороной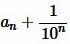 
(Рис.4), т.е.
При неограниченном увеличении числа n, число 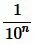будет становиться сколь угодно малым и, следовательно, число 
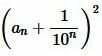будет сколь угодно мало отличаться от 
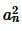. Тогда из неравенства (5) следует, что число S будет мало отличаться от числа 
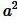. Следовательно они равны, т.е. .
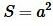Площадь квадрата по стороне
Из вышеизложенного доказательства получили, что площадь квадрата равна:
где ( small a ) сторона квадрата.
Пример 1. Сторона квадрата равна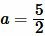 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (6). Подставляя 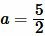в (6), получим:
Ответ: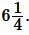 
Площадь квадрата по диагонали
Пусть известна диагональ ( small d ) квадрата (Рис.5). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Для этого воспользуемся теоремой Пифагора:
Подставляя (7) в (6), получим:
то есть площадь квадрата по диагонали вычисляется из следующей формулы:
Пример 2. Диагональ квадрата равна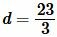 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (8). Подставляя 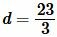в (8), получим:
Ответ: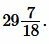 
Площадь квадрата по радиусу вписанной окружности
Пусть известен ( small r ) радиус окружности вписанной в квадрат (Рис.6). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Нетрудно заметить, что радиус ( small r ) равна половине стороны ( small a ) квадрата, т.е.
Подставляя (9) в (6), получим:
или
Пример 3. Радиус вписанной в квадрат окружности равен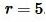 
. Найти площадь квадрата.
Решение. Для нахождения плошади квадрата воспользуемся формулой (10). Подставляя 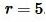в (10), получим:
Ответ: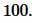 
Площадь квадрата по радиусу описанной окружности
Пусть известен ( small R ) радиус окружности описанной около квадрата (Рис.7). Найдем площадь квадрата.
Для нахождения плошади квадрата, найдем сначала сторону ( small a ) квадрата. Восрользуемся теоремой Пифагора:
Подставляя (11) в (6), получим:
Пример 4. Радиус описанной окружности равен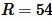 
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (12). Подставляя 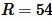в (12), получим:
Ответ: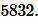 
Площадь квадрата по периметру
Пусть известен периметр ( small P ) квадрата. Найдем площадь квадрата. По периметру можно найти сторону квадрата:
Подставляя (13) в (6), получим:
то есть площадь квадрата через периметр равна:
Пример 5. Периметр квадрата равен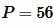 
. Найти площадь квадрата.
Решение. Для нахождения площади квадрата воспользуемся формулой (14). Подставляя 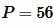в (14), получим:
Ответ: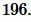 
Смотрите также:
- Квадрат. Онлайн калькулятор
{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат – четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a – сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d – диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r – радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R – радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P – периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .
