Как рассчитать площадь усеченного конуса
На данной странице калькулятор поможет рассчитать площадь поверхности усеченного конуса онлайн. Для расчета задайте радиусы и образующую.
Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образующая конуса – это отрезок, соединяющий вершину и границу основания.
Боковая поверхность
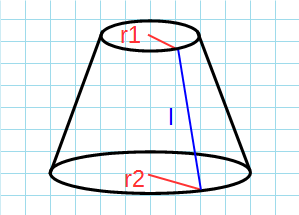
Формула площади боковой поверхности усеченного конуса через радиусы и образующую:
π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; l – образующая усеченного конуса.
Полная поверхность

Формула площади полной поверхности усеченного конуса через радиусы и образующую:
π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; l – образующая усеченного конуса.
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.
-
Формулы вычисления площади усеченного конуса
-
1. Боковая поверхность
- 2. Основания
- 3. Полная площадь
-
1. Боковая поверхность
- Пример задачи
Формулы вычисления площади усеченного конуса

Примечание: иногда усеченный конус, также, называют коническим слоем.
1. Боковая поверхность
Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.
Sбок. = πRl + πrl = πl(R + r)
Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.
2. Основания
Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:
Sосн.1 = πR 2
Sосн.2 = πr 2
Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.
3. Полная площадь
Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.
Sполн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2)
Пример задачи
Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.
Решение
Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.
Sбок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см2
Sосн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см2
Sосн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см2
Sполн. = 427,04 см2 + 379,94 см2 + 113,04 см2 = 920,02 см2
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой – сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
Конус — это геометрическое тело, которое образовано совокупностью всех лучей,
исходящих из точки (вершины конуса) и пересекающих любую плоскую поверхность. В месте пересечения образуется основание конуса.
Круглый конус – это тело, состоящее из круга (основание конуса), точки,
которая не лежит в плоскости этого круга (вершина конуса и всех отрезков, которые соединяют вершину конуса с точками основания).
Круглый конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
Усеченный конус — это часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.
Под усеченным конусом имеется ввиду часть прямого кругового конуса.
Такой усеченный конус образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.
Каждая объемная фигура, которая имеет конечные линейные размеры, обладает в пространстве некоторой площадью поверхности. В статье рассмотрим, чему равна площадь боковой поверхности конуса, приведем соответствующие формулы и покажем, откуда они выводятся.
Что такое конус?
В общем случае конусом в геометрии называют любую пространственную фигуру, которая образована в результате соединения фиксированной точки пространства со всеми точками некоторой плоской кривой. Фиксированная точка называется вершиной фигуры. Отрезки, соединяющие ее с кривой, получили название генератрис, или образующих, поскольку их совокупность образует коническую поверхность. Кривая, на которую опирается эта поверхность, называется директрисой, то есть направляющей. Директрисой может быть произвольная кривая, например, гипербола, окружность, парабола, эллипс и так далее. Образованный на них конус будет гиперболическим, круглым, параболическим и эллиптическим, соответственно.

Выше рисунок демонстрирует пример двух одинаковых эллиптических конусов, обращенных друг к другу своими вершинами.
Круглый конус
Площадь боковой поверхности конуса будем рассматривать на примере круглой прямой фигуры. Такой конус представляет собой круглое основание, на которое опирается коническая поверхность. Эта фигура показана ниже.

Все генератрисы этой фигуры равны между собой. Их длина всегда больше радиуса основания. Расстояние от вершины конуса до его круглого основания называется высотой. Высота пересекает круг в его центре, поэтому конус называется прямым.
Получить этот конус не представляет никакой сложности. Для этого следует взять любой треугольник, имеющий прямой угол, и вращать его вокруг одного из катетов так, как показано ниже на схеме.

Если обозначить гипотенузу этого треугольника буквой g, а его катеты h и r, тогда будет справедливо равенство:
g2 = h2 + r2.
Для полученного конуса g — это генератриса, h — высота, r — радиус круга.
Чему равна боковая поверхность конуса с круглым основанием?
Ответить на этот вопрос проще всего, если разрезать коническую поверхность вдоль одной из генератрис и развернуть ее на плоскости. Получившаяся фигура называется разверткой боковой поверхности. Она показана на главном фото к статье, где также приводится круг — основание фигуры.
Эта развертка показывает, что площадь боковой поверхности конуса равна площади соответствующего кругового сектора. Он ограничен двумя генератрисами g, которые представляют радиус полного круга, и дугой. Длина последней точно равна длине окружности основания. Получим формулу для площади этого сектора.
Сначала определим угол в радианах, соответствующий дуге сектора. Его можно найти с использованием следующей пропорции:
2*pi ==> 2*pi*g;
x ==> 2*pi*r.
Здесь 2*pi*g — это длина всей окружности, ограничивающей рассматриваемый сектор, 2*pi*r — это длина дуги сектора. Угол в радианах x сектора будет равен:
x = 2*pi*r*2*pi/(2*pi*g) = 2*pi*r/g.
Для определения площади рассматриваемого сектора, следует воспользоваться пропорцией через соответствующие площади. Имеем:
2*pi ==> pi*g2;
2*pi*r/g ==> Sb.
Здесь pi*g2 является площадью круга, построенного с помощью образующей g, Sb — площадь боковой поверхности конуса, равная площади рассматриваемого кругового сектора. Результатом решения пропорции будет конечная формула для Sb:
Sb = pi*g2*2*pi*r/g/(2*pi) = pi*r*g.
Таким образом, чтобы найти площадь конической поверхности, достаточно умножить радиус фигуры на ее директрису и на число пи.
При получении конечной формулы для Sb через пропорции использовалось свойство равенства угла полной окружности числу 2*pi радиан.
Понятие о конусе усеченном
Пусть имеется круглый прямой конус. Возьмем плоскость и отсечем от этой фигуры верхнюю часть таким образом, чтобы секущая плоскость прошла параллельно основанию конуса. Оставшаяся под плоскостью фигура называется прямым усеченным конусом с параллельными основаниями. Он показан на рисунке ниже.

В отличие от исходной фигуры, усеченный конус образован тремя поверхностями:
- малое круглое основание;
- большое круглое основание;
- часть конической поверхности.
Последняя в списке является боковой поверхностью для рассматриваемой фигуры.
Для усеченной фигуры справедливы те же понятия, что для полного конуса. Так, расстояние между его основаниями — это высота h, каждое основание имеет свой радиус (r1 и r2). Часть генератрисы исходного конуса теперь является генератрисой конуса усеченного. Обозначим ее буквой l.
Между отмеченными линейными параметрами существует следующая связь:
l2 = h2 + (r1-r2)2.
Боковая поверхность усеченной фигуры
Выше было сказано, что представляет собой боковая поверхность для конуса усеченного. Разрезая ее вдоль одной из генератрис, получим следующий результат.

Два круга представляют собой основания. Четырехугольная фигура, ограниченная двумя прямыми отрезками и двумя дугами — это искомая боковая поверхность усеченного конуса, площадь которой необходимо найти. Решим эту задачу.
Заметим, что эта поверхность представляет собой сектор круга, у которого вырезана центральная часть. Обозначим радиус внешней дуги как g. Тогда радиус внутренней дуги будет равен g — l. Используя результаты решения предыдущей пропорции при определении угла сектора x, можно записать следующее равенство:
x = 2*pi*r1/g = 2*pi*r2/(g-l) =>
g = l*r1/(r1-r2).
Искомая площадь Sb равна разнице площадей секторов, построенных с помощью радиусов g и g-l. Используя формулу для площади сектора, полученную выше, можно записать:
Sb = pi*g*r1 — pi*(g-l)*r2.
Подставляя в это выражение формулу для g, получаем конечное равенство для площади боковой поверхности конуса усеченного:
Sb = pi*l*(r1+r2).
Задача на определение площади конической поверхности
Решим простую задачу. Необходимо найти площадь боковой поверхности конуса, если известно, что его высота h равна диаметру основания, а генератриса составляет 15 см.
Запишем соответствующую формулу для Sb, из которой будет видно, какие величины следует рассчитать. Имеем:
Sb = pi*r*g.
Значение генератрисы g известно из условия задачи. Остается определить радиус фигуры.
Генератриса, высота и радиус связаны друг с другом следующим равенством:
g2 = h2 + r2.
Из условия следует, что 2*r = h. Подставляя значение h в выражение, получим:
g2 = (2*r)2 + r2 = 5*r2 =>
r = g/√5.
Теперь формулу для радиуса основания подставляем в выражение для Sb, получаем:
Sb = pi/√5*g2.
Мы получили конечную формулу, из которой видно, что площадь искомой поверхности зависит только от длины генератрисы. Подставляя g = 15 см, получаем ответ на задачу: Sb ≈ 315,96 см2.
Просмотры: 53
