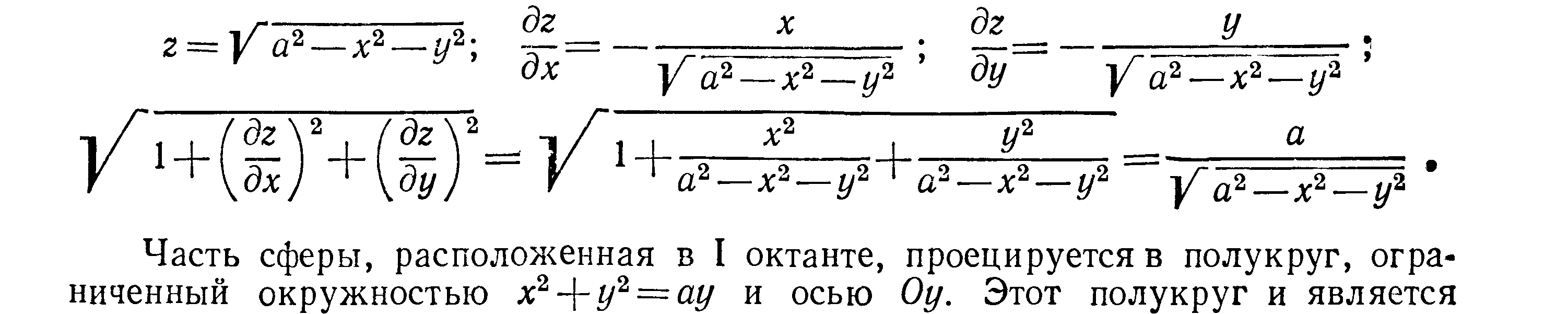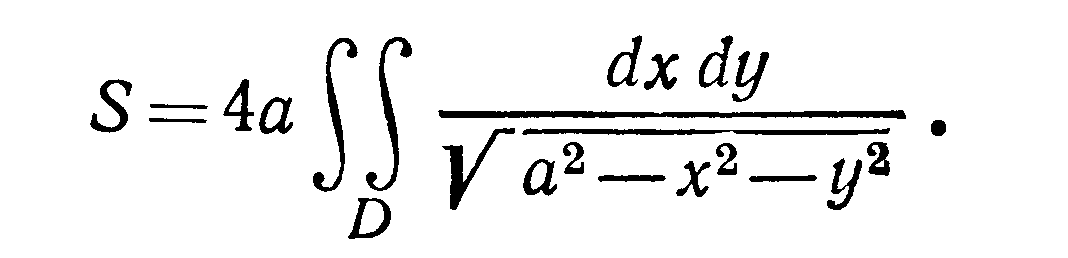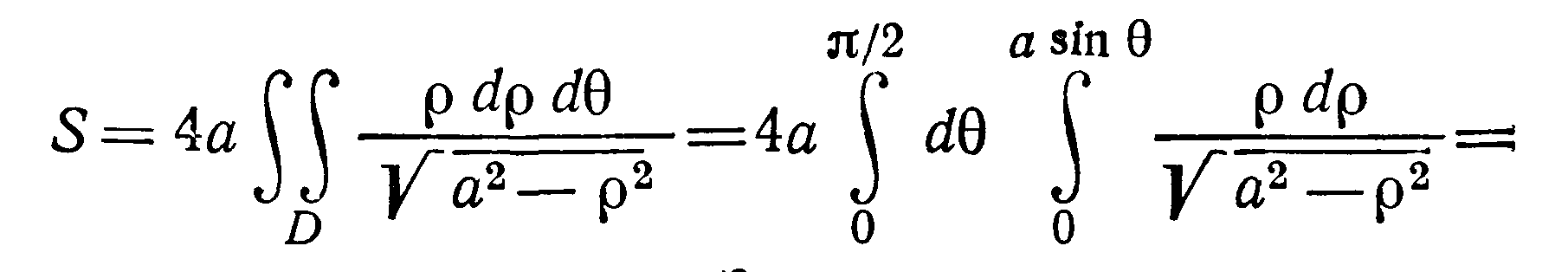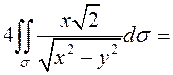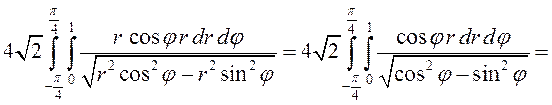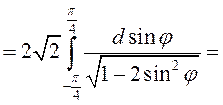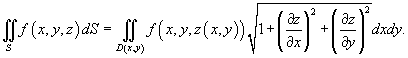Как найти площадь части поверхности вырезаемой

Задачи с решениями

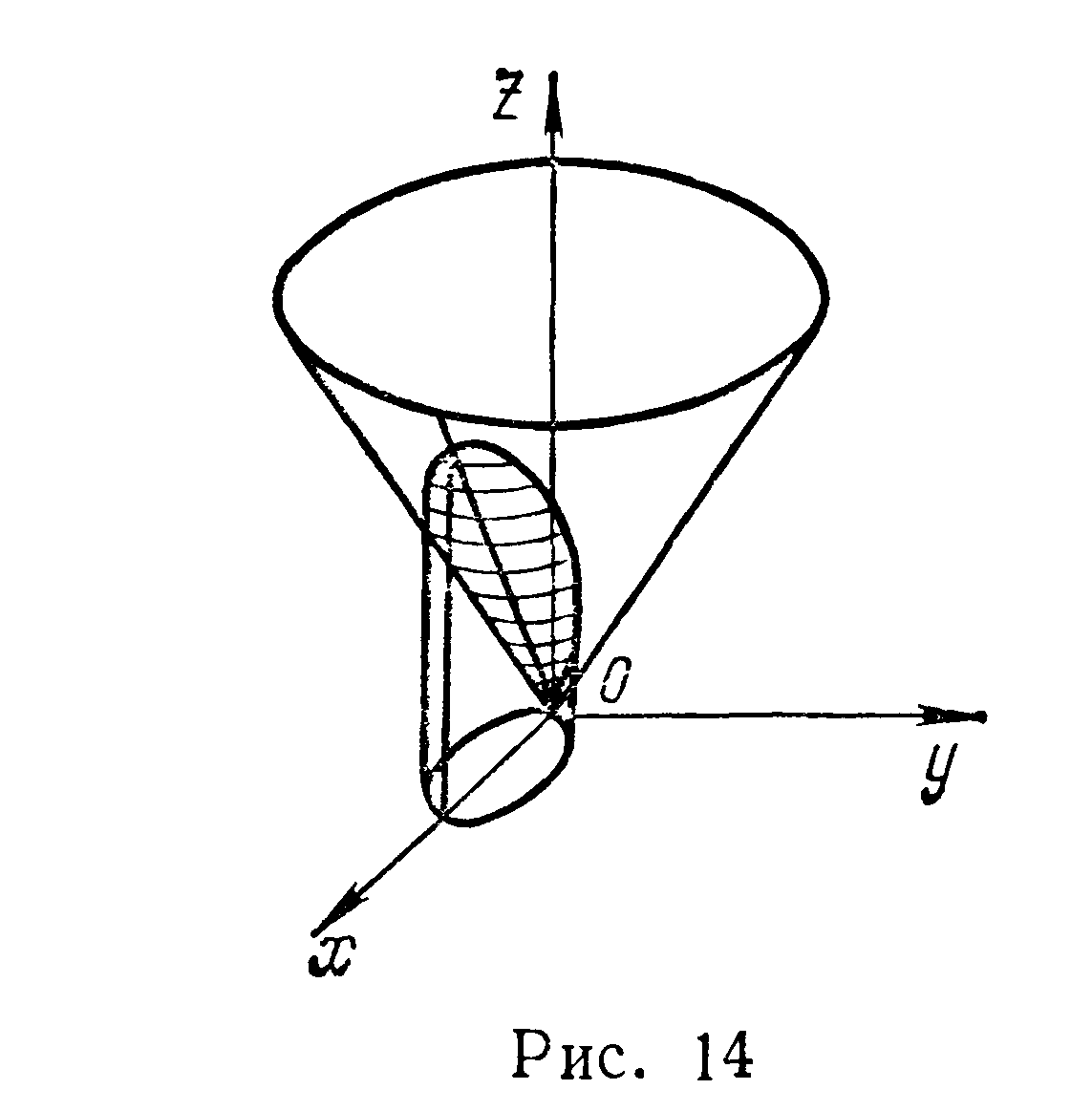
1. Найти площадь части сферы
   

   заключенной внутри цилиндра
   

Решение Из уравнения сферы имеем
(для I октанта):

областью интегрирования D.
Поверхность расположена в четырех
октантах потому искомая площадь

Перейдем к полярным координатам, тогда
уравнение окружности примет вид

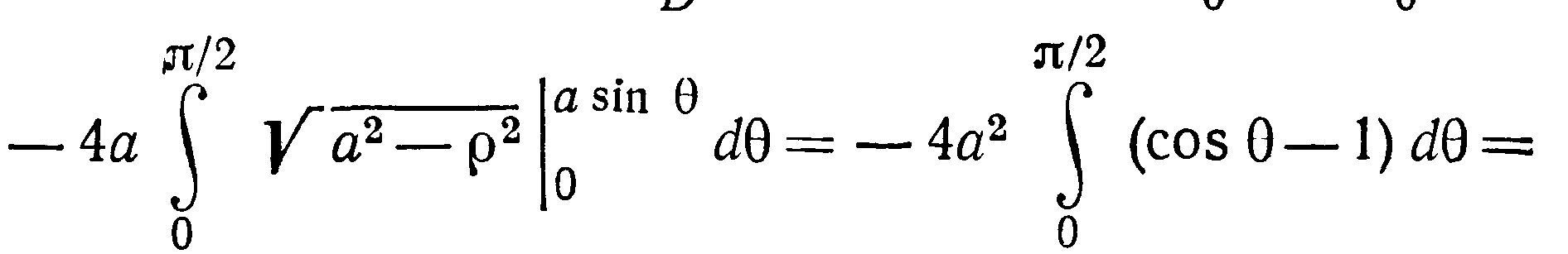
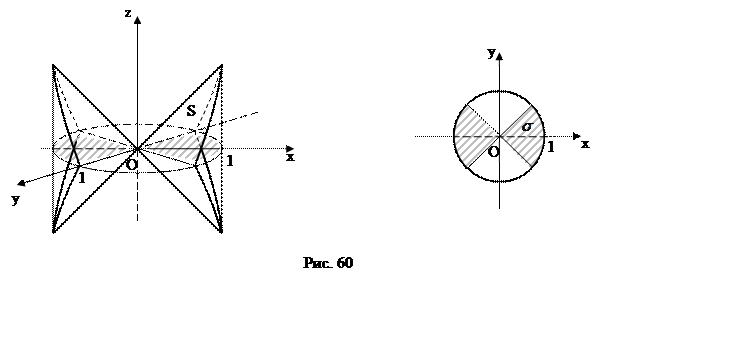
1. Найти площадь части конуса
   

   внутри цилиндра
   

Решение Из уравнения конуса
имеем

Областью
интегрирования D является круг,
ограниченный окружностью

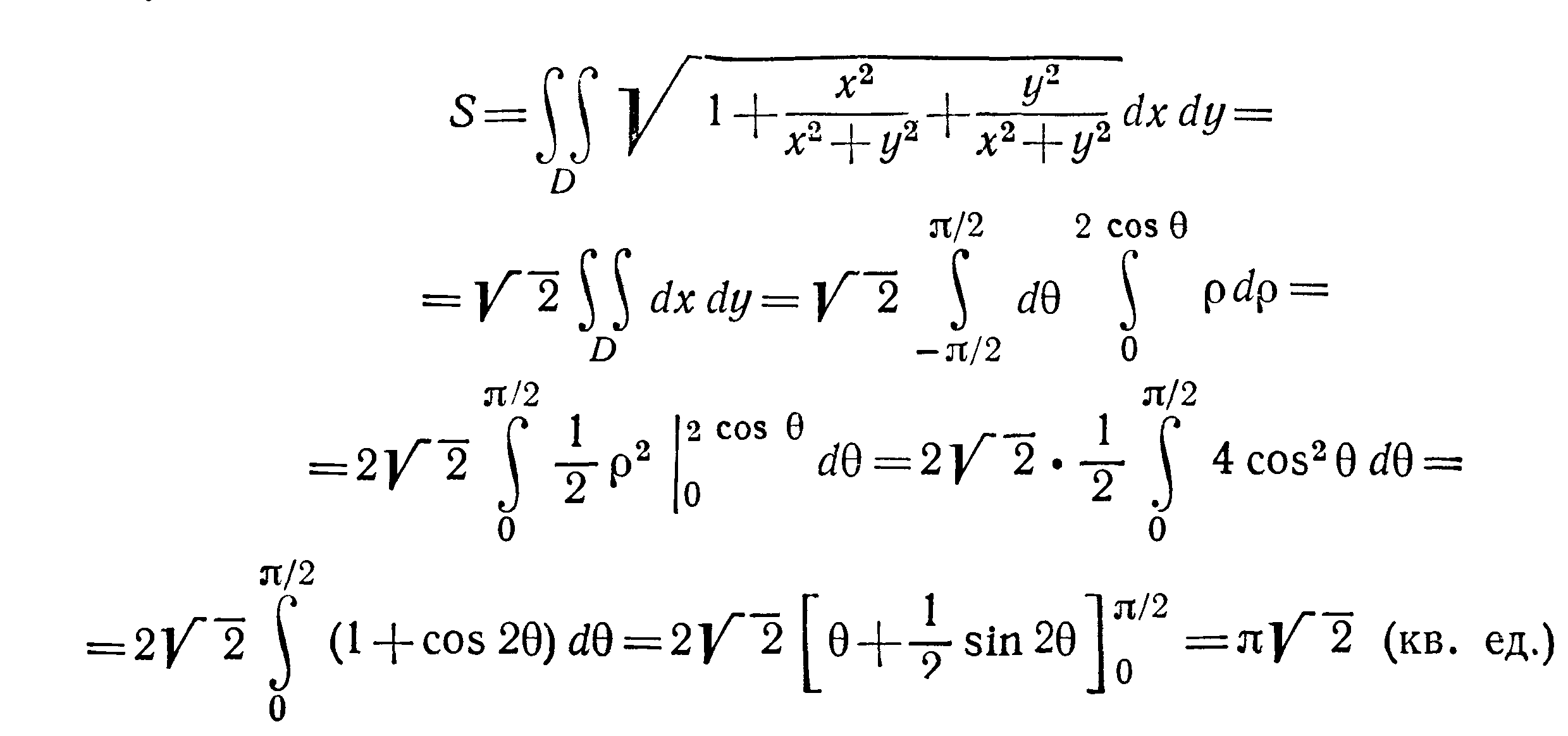
1. Вычислить площадь поверхности цилиндра

   

   отсеченной плоскостями
   

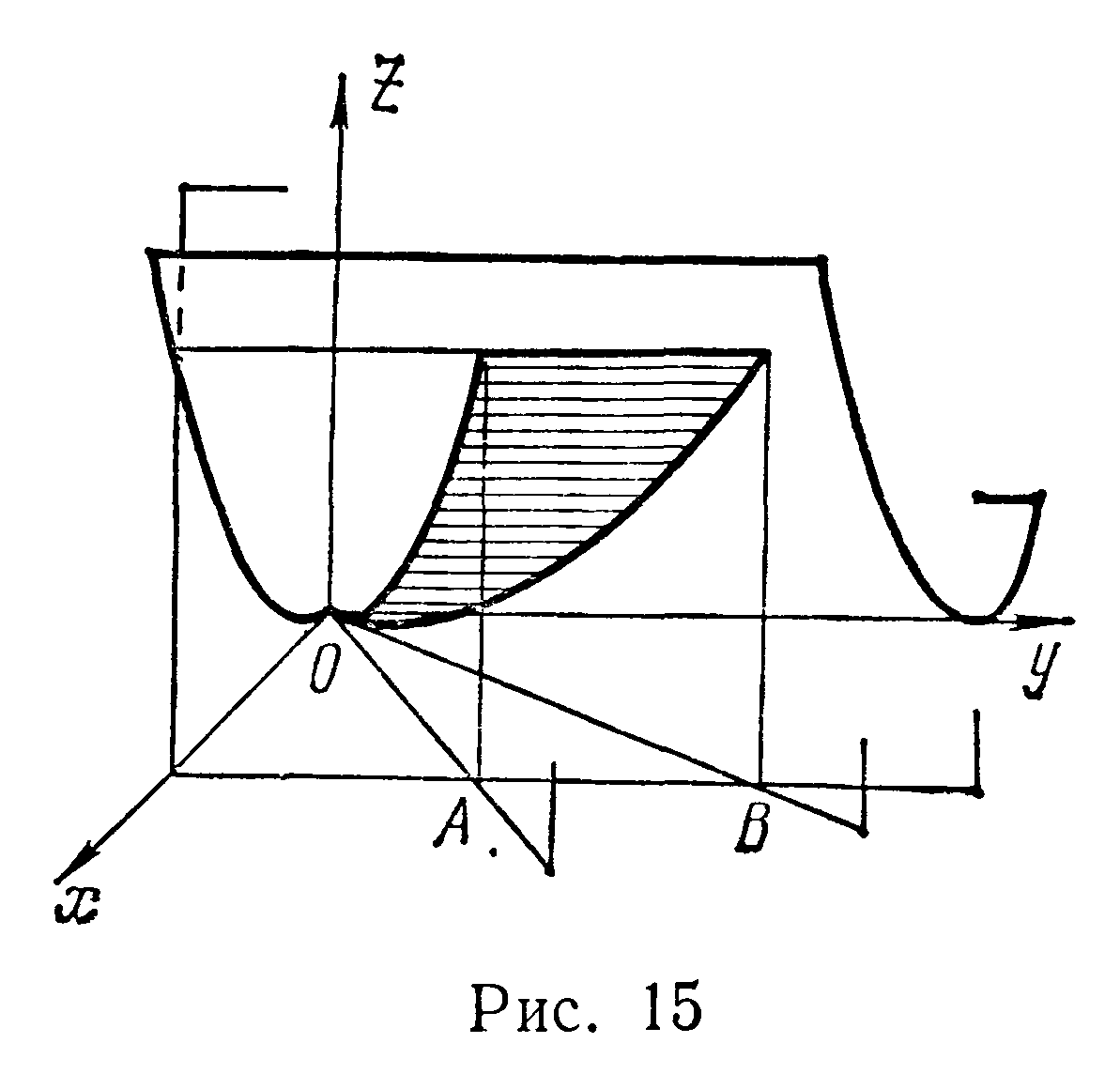
Решение Областью интегрирования
служит треугольник ОАВ. Из уравнения
цилиндра имеем

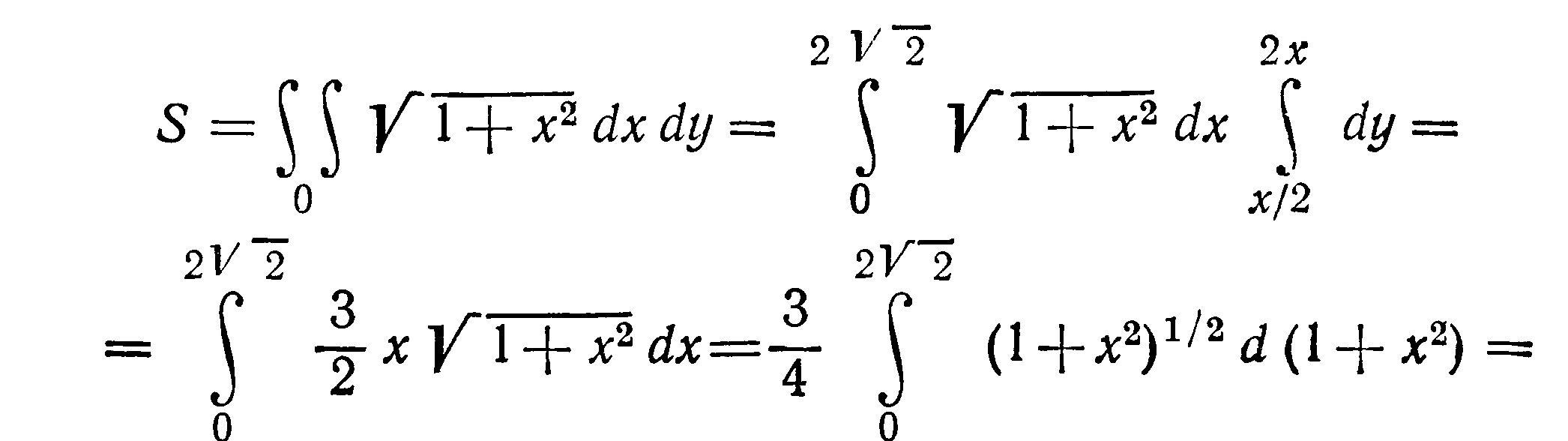
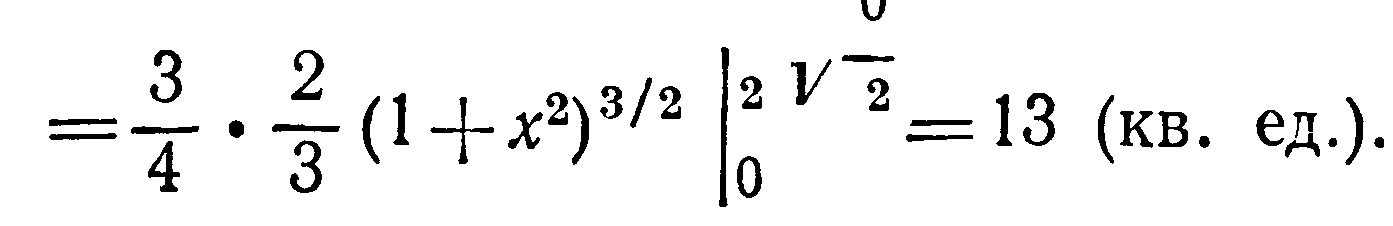
1. Вычислить площадь части поверхности
   параболоида x
   
   ,
   вырезанной цилиндром
   

Решение Область интегрирования
– окружность

(она расположена в плоскости yOz).
Из уравнения параболоида имеем

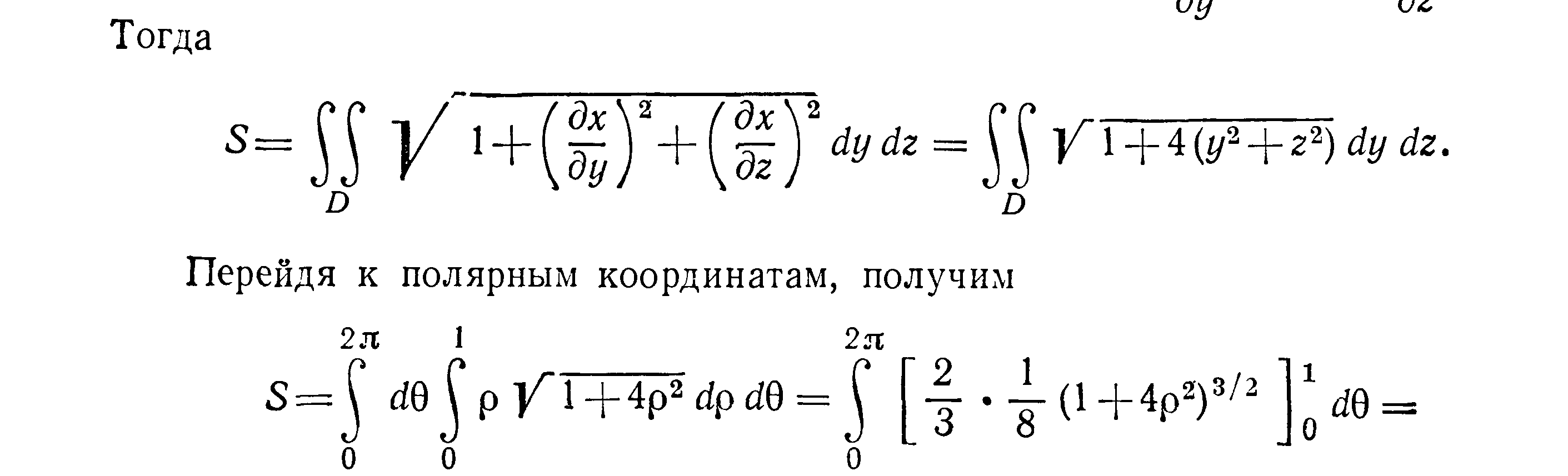
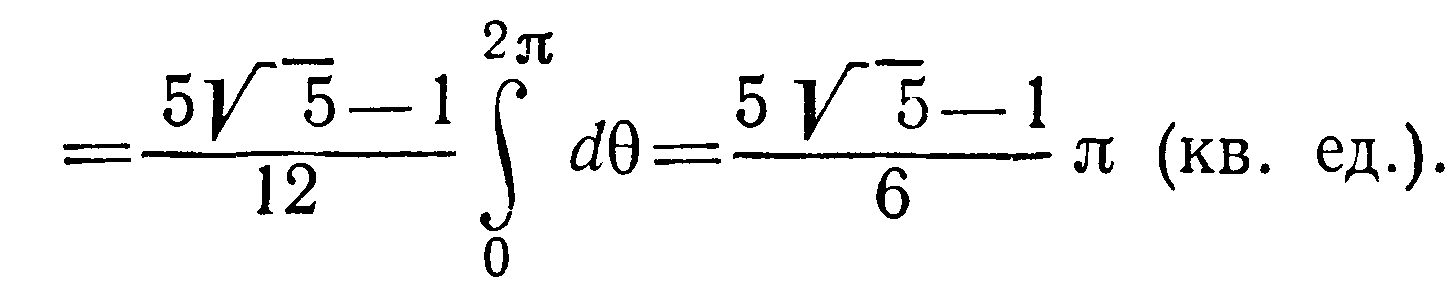
Задачи

36 . Найти площадь части поверхности

вырезанной цилиндром

37. Найти площадь части сферы

вырезанной цилиндром

38. Найти площадь той части плоскости z=
x:, которая заключена
внутри цилиндра

39. Найти площадь части поверхности
цилиндра z = x²,
вырезанной плоскостями

40. Вычислить площадь поверхности конуса

расположенной внутри цилиндра

41. Вычислить площадь поверхности цилиндра

расположенной внутри цилиндра

42. Найти площадь части поверхности

вырезанной плоскостями

Индивидуальные задания

Тройной интеграл

Пусть функция f (х, у, z)
определена в ограниченной замкнутой
пространственной области Т. Разобьем
область Т произвольным образом на п
элементарных областей T₁
Т₂, …, Т_n с
диаметрами d₁ d₂,
…, dn и объемами ∆V₁,
∆V_{2, ….,}∆Vn.
В каждой элементарной области возьмем
произвольную точку P_k
(ξ₁, ξ₂, … , ξ_n
) и умножим значение функции в точке Р_k
на объем этой области.

Интегральной суммой для функции f
(х, у, z) по области Т
называется сумма вида

Предел интегральной суммы при стремлении
к нулю наибольшего из диаметров всех
элементарных областей ∆Vk
называется тройным интегралом от функции
f (х, у, z) по
области Т и обозначается следующим
образом:

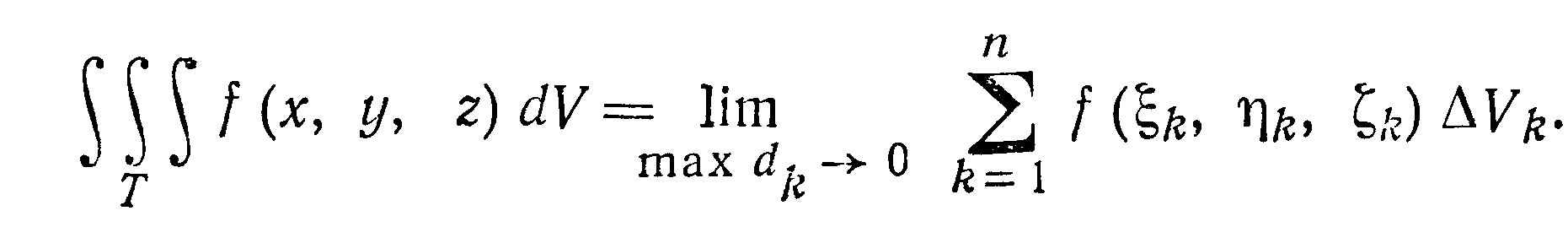
Конечный предел такого вида может
существовать только для ограниченной

функции.

Если f (х, у, z)
> 0 в области Т, то тройной интеграл

представляет собой массу тела, занимающего
область Т и имеющего переменную плотность
γ = f(x, у, z)
(физическое истолкование тройного
интеграла).

Основные свойства тройных интегралов
аналогичны свойствам двойных интегралов.

В декартовых координатах тройной
интеграл обычно записывают в виде

Пусть область интегрирования Т
определяется неравенствами x₁≤
x≤ x_2, y₁≤
y ≤ y_2,
z₁≤ z
≤ z_2, где y₁(x),
y₂(x),
z₁(x,y),
z₂ (x,y)
непрерывные функции. Тогда тройной
интеграл от функции f (х,
у, z), распространенный на область Т,
вычисляется по формуле

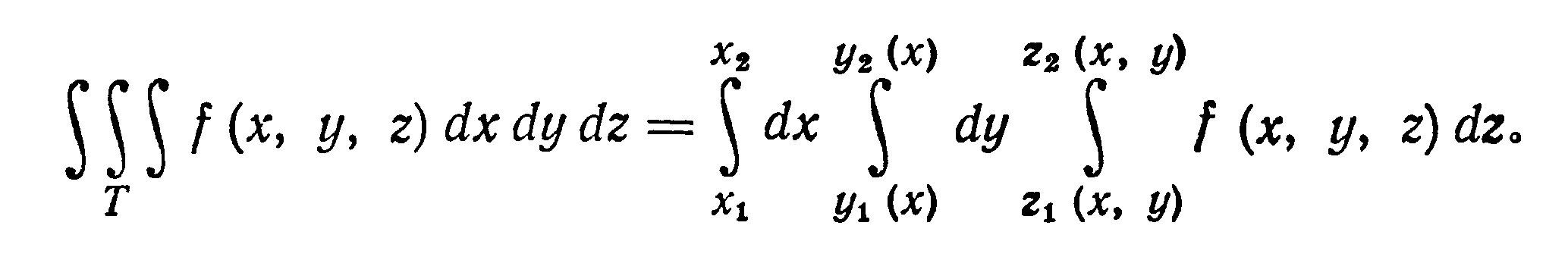
Если при вычислении тройного интеграла
требуется перейти от переменных х, у, z
к новым переменным и, v, w, связанным с х,
у, z соотношениями х = х(u,
v, w), y = y(u, v, w), z = z (u, v, w), где
функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные
вместе со своими частными производными
первого порядка, устанавливают взаимно
однозначное и в обе стороны непрерывное
соответствие между точками области Т
пространства Oxyz и точками некоторой
области Т’ пространства Ouvw и якобиан J
в области Т’ не обращается в нуль

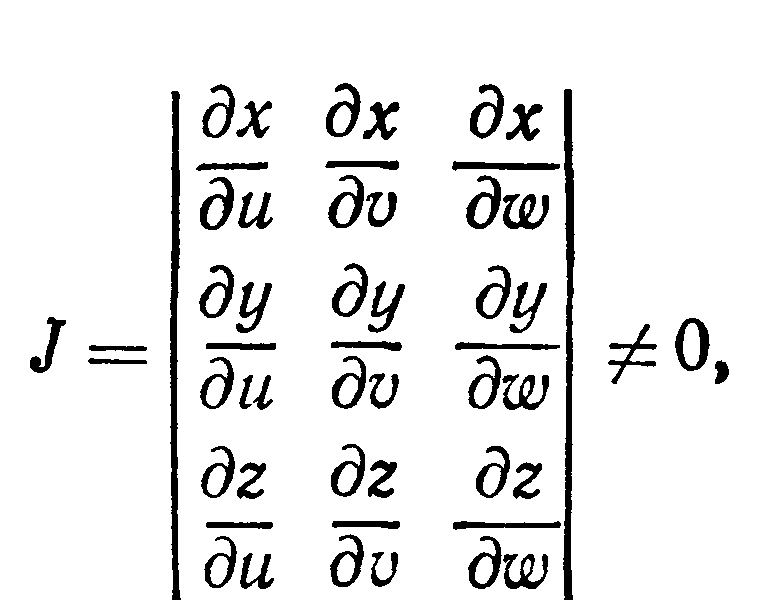
то пользуются формулой

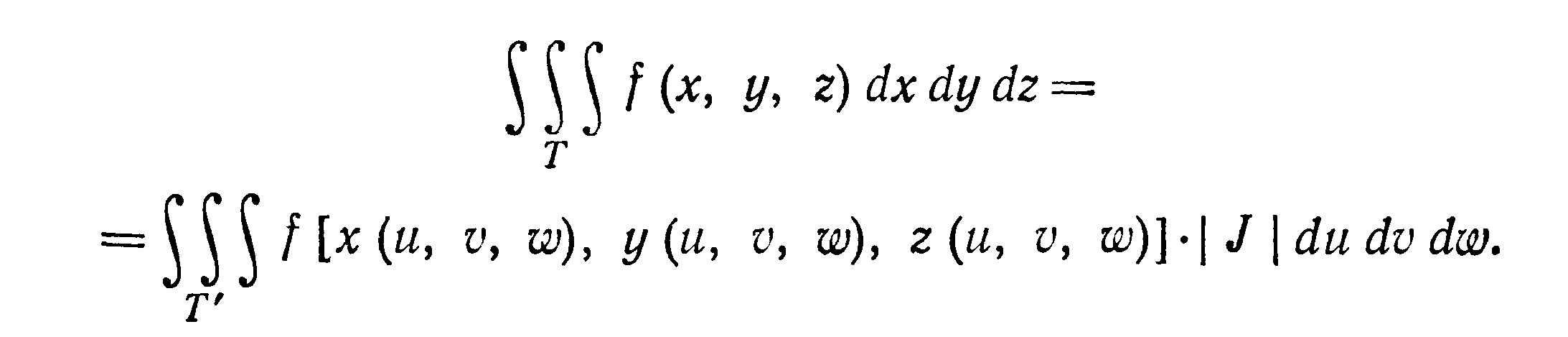
В частности, при переходе от декартовых
координат х, у, z к
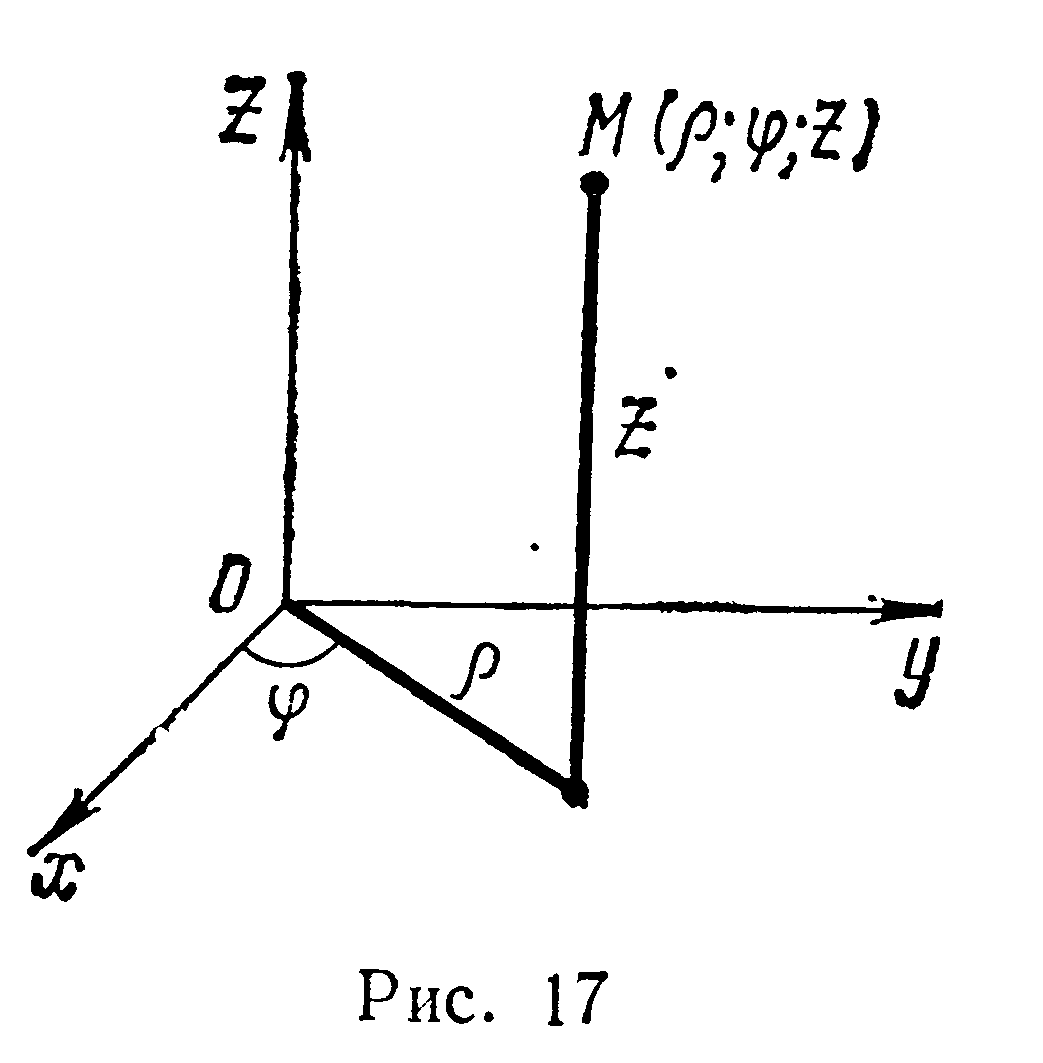
цилиндрическим координатам ρ,φ , z
(рис. 17), связанным с х, у, z
соотношениями

якобиан преобразования J = ρ
и формула преобразования тройного
интеграла

к цилиндрическим координатам имеет вид

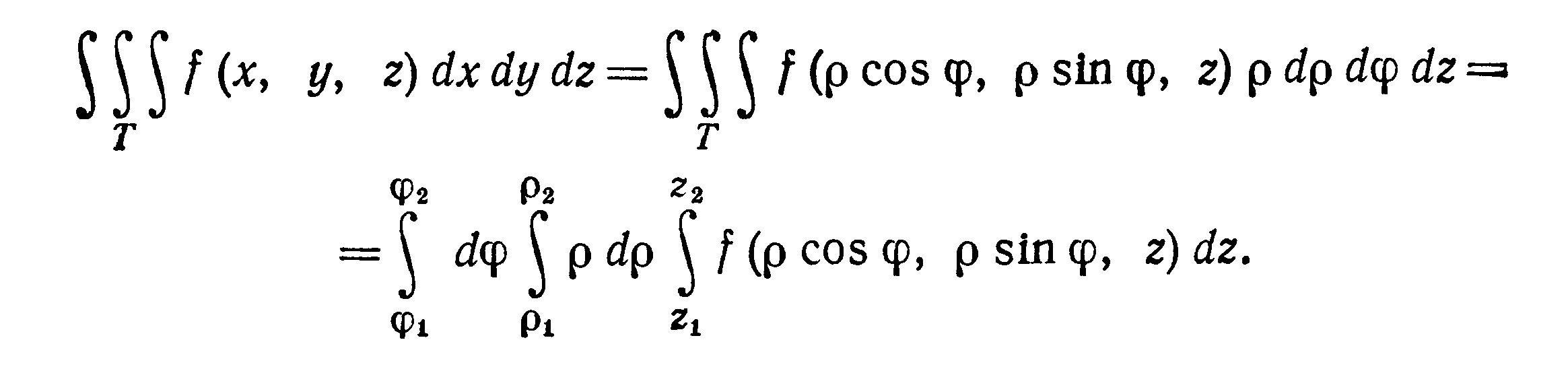
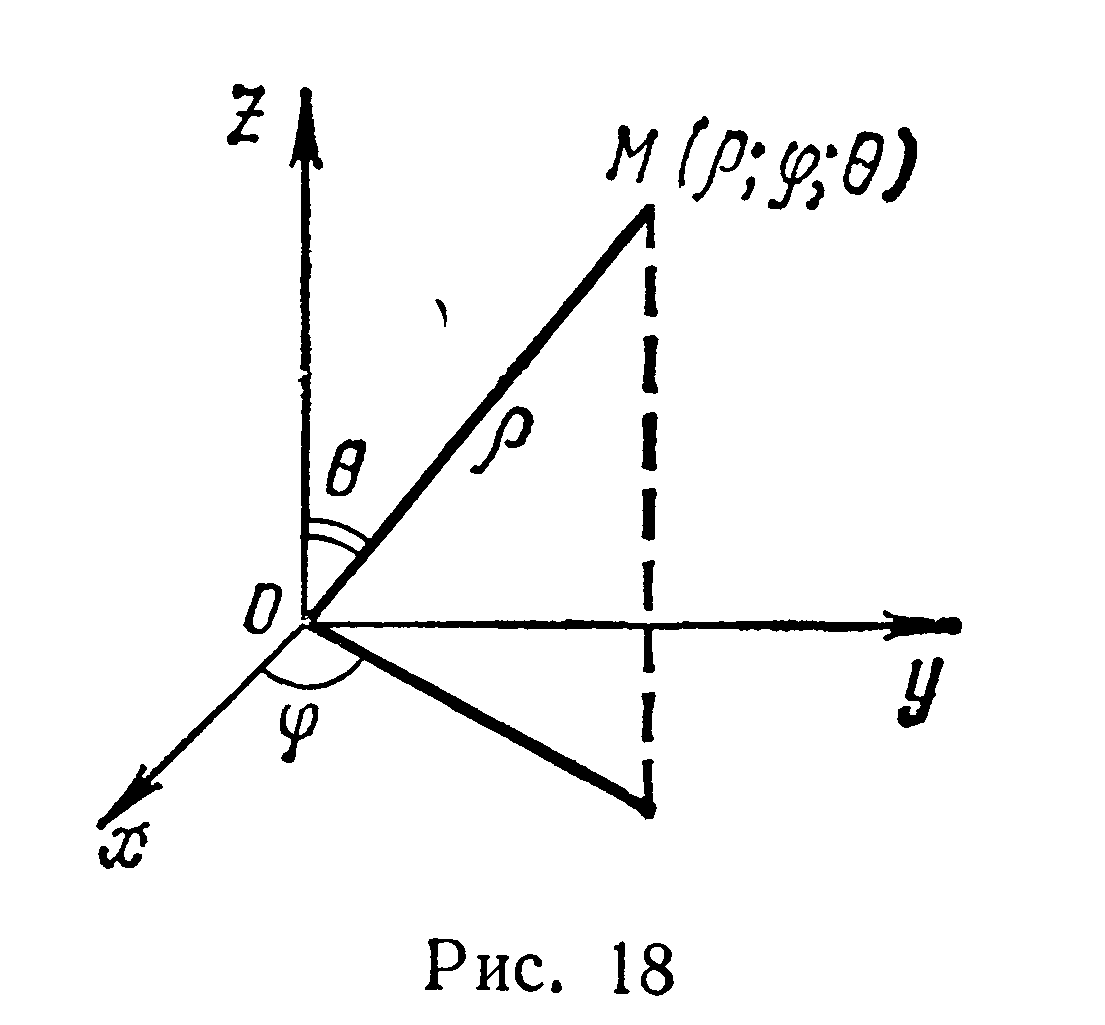
При переходе от декартовых координат
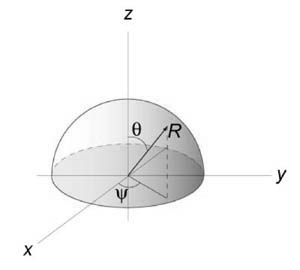
х, у, z к сферическим координатам ρ,φ,θ
(рис. 18), связанным с х, у, z соотношениями

якобиан преобразования J
= ρ² sinθ, и формула
преобразования тройного интеграла к
сферическим координатам имеет вид

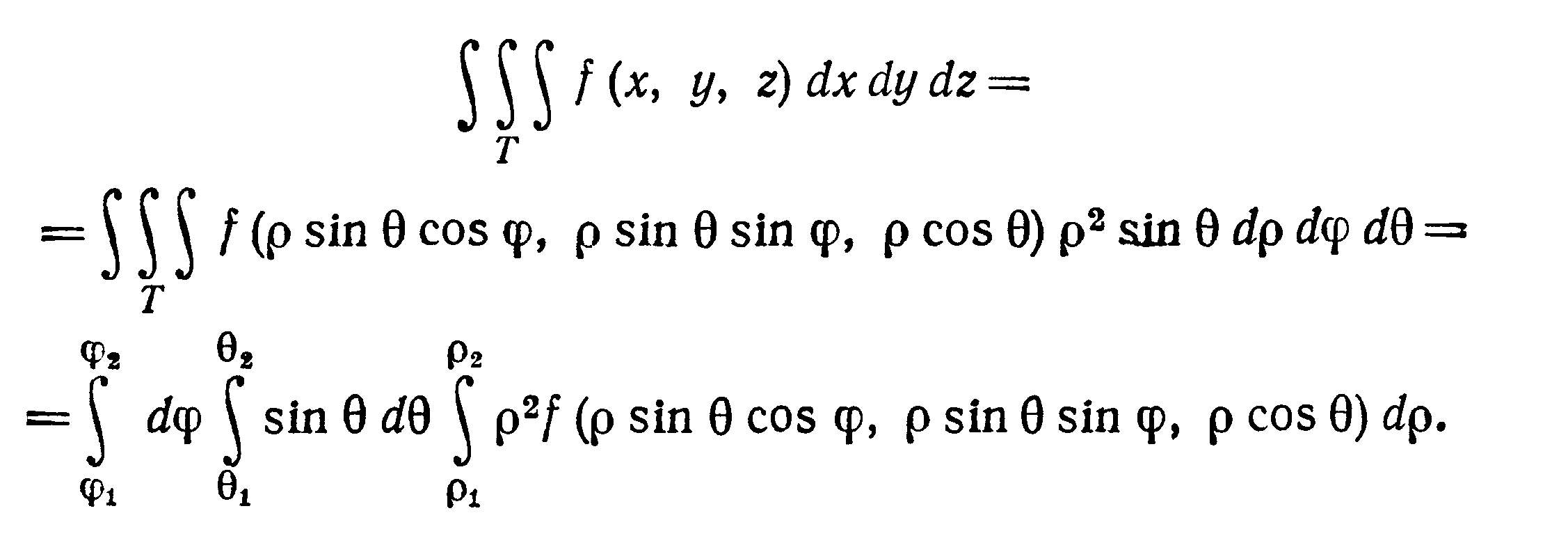
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Случай явного задания поверхности. ПлощадьГладкой поверхности Выражается формулой

(19.19)

Где– проекция данной поверхности на плоскость

Если поверхность имеет уравнение видаТо

(19.20)

Где— проекция поверхности на ось

Если поверхность задана уравнением,, то

(19.21)

Где— проекция поверхности на ось

Случай неявного задания поверхности. ПлощадьПоверхности, заданной уравнениемВыражается интегралом

(19.22)

Где– проекция поверхности на плоскость

Случай параметрического задания поверхности. Если поверхность задана параметрическими уравнениями

Где– ограниченная замкнутая квадрируемая область, в которой

Функции х, у, z непрерывно дифференцируемы, то

(19.24)

Где

(19.25)

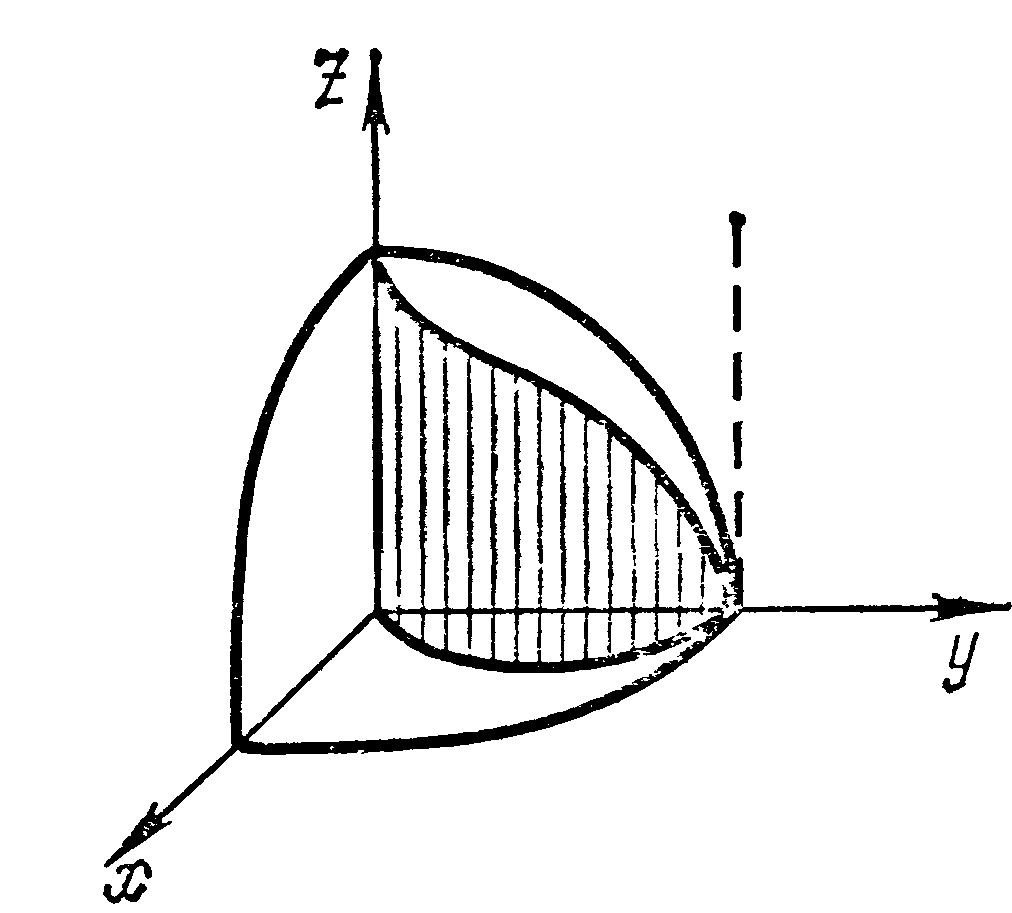
Пример 19.17. Найти площадь части поверхности цилиндра Заключенной внутри сферы(боковая поверх

Ность «тела Вивиани», рис. 19.19).

Применим формулу (19.20). Поскольку плоскостьюЦилиндр разделяется на две равные части, то можно вычислить половину искомой площади поверхности. Вычислим площадь той части поверхности, уравнение которой Для определения области интегрирования следует спроецировать на плоскость линию пересечения поверхностей, уравнение которой находится исключениемИз данных уравнений. Вычитая одно уравнение из другого, получаемЭто

Так как

Уравнение параболы, лежащей в плоскости С вершиной на осиНа расстоянии от начала координат и пересекающей ось в точкахДуга указанной

Параболывместе с соответствующим отрезком осиСоставляют границу области.

Пример 19.18. Вычислить площадь поверхности конуса , заключенной внутри цилиндра Цилиндр отсекает на поверхности конуса две части, симметричные относительно плоскостиНа рис. 19.20 изображена только верхняя частьВычислим пло

ИшьЭтой части, проекция которой на плоскостьЕсть круг

Так как для рассматриваемой части конуса

То по формуле (19.19)

Получаем

Где– окружность Переходя к полярным координатам, находим

Следовательно, вся искомая площадь

Пример 19.19. Найти площадь поверхности, вырезанной цилиндром Из сферы

Цилиндр вырезает из сферы две части, верхняя из них изображена на рис. 19.21. Вычислим площадьПоверхности этой сферы. Для верхней полусферы

Следовательно,– круг

Переходя к полярным координатам, находим 338

Итак,

Рис. 19.20

Пример 19.20. Вычислить площадь частей сферы вырезанных из нее цилиндромВоспользовавшись параметрическими

Уравнениями сферической поверхности:

Рис. 19.21

Здесь вдет речь о вычислении площади верхнего и нижнего оснований «тела Вивиани» (см. рис. 19.19). Воспользуемся формулой (19.24), для чего предварительно найдем коэффициентыТак как

То по формулам (19.25)

НаходимСледовательно,

Ограничимся рассмотрением четверти изучаемой поверхности, лежащей в первом октанте. Для точек «кривой Вивиани», т. е. кривой пересечения сферы и цилиндра (в пределах первого октанта),Действительно подставляя выраженияИЧерезИВ уравнение цилиндраПолучаем И поскольку для рассматриваемых точек, очевидно, , то отсюда следует, что

Установив на основании сказанного пределы измененияИПо формуле (19.24) получим

< Предыдущая		Следующая >

ЗАМЕЧАНИЕ. Если поверхность  удобно
проецировать на другую координатную плоскость, то формулы (8.17) и (8.18)
соответствующим образом изменятся.

ПРИМЕР.
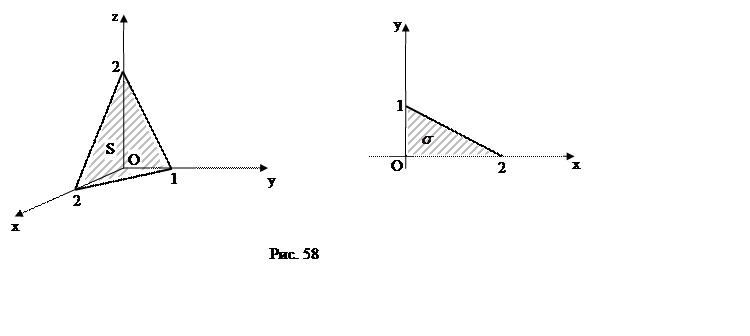
Вычислить 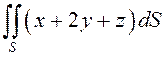, если  часть
плоскости  , расположенная в первом октанте (рис.58).      

Из уравнения
плоскости получим:

. Кроме того, во
всех точках плоскости , поэтому   – по свойству 1 определённого интеграла:
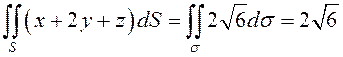
площадь проекции  (рис.58), очевидно, равна 1.

Рассмотрим немного более сложный пример.

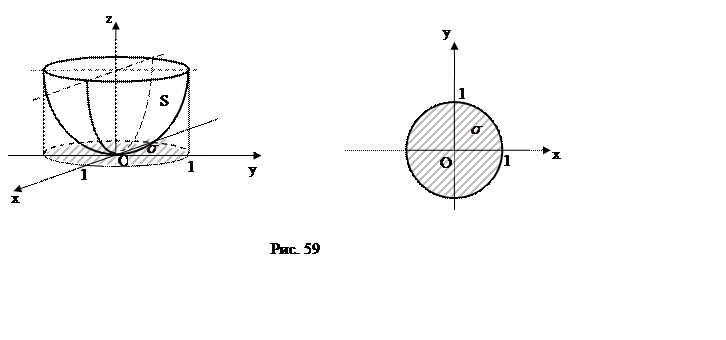
ПРИМЕР. Вычислить 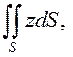если часть поверхности эллиптического
параболоида , вырезаемая из него цилиндром  (рис.59).

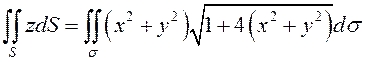
Так как на  и , то, пользуясь (8.17) и (8.18), получим .  Проекция  поверхности
 на плоскость  – круг
(рис.59), поэтому перейдем в двойном интеграле к полярным координатам:

(Замена )

.

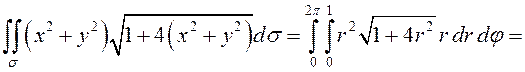
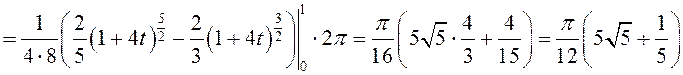
ЗАМЕЧАНИЕ. Площадь поверхности, задаваемой уравнением , согласно свойству 1 определенного
интеграла и (8.17) вычисляется по формуле:

                                                        (8.19)

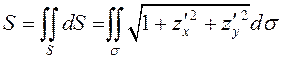
ПРИМЕР. Вычислить площадь части поверхности конуса , вырезаемой из него цилиндром  (рис.60).   

На верхней правой четверти этой
поверхности, где ,  

.

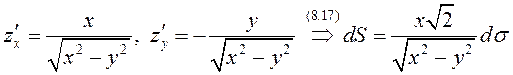
Отсюда
                                  .

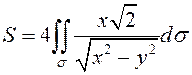
Так  как проекция    этой части
поверхности  на плоскость  – круговой сектор  (рис.60),  то  будем вычислять полученный
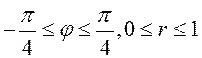
двойной интеграл в полярных координатах:

.

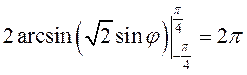
8.14. Вычисление тройного интеграла

в декартовых координатах

Пусть в пространственной области  задана непрерывная функция . По определению тройным интегралом от этой
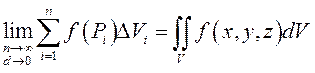
функции по области  называется , где точки  , а  – малые части области , на которые она разбивается при
составлении интегральной суммы.

Для вычисления тройного интеграла в декартовых
координатах разобьем   на достаточно малые части
плоскостями  . Тогда  – параллелепипед со сторонами , поэтому, очевидно, элемент объема .

Заметим, что плоскости  являются
координатными поверхностями декартовой системы координат  (аналогично координатным линиям  системы координат ):
на каждой из этих плоскостей изменяются лишь две из трех координат .

По аналогии с двойным интегралом для того, чтобы
вычислить тройной, надо расставить пределы интегрирования, то есть свести
тройной  интеграл к трехкратному.

Начнем
с самой простой области в системе .

1.  – параллелепипед, грани которого
параллельны координатным плоскостям:  .

В
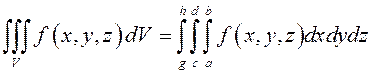
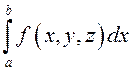
этом случае  . Внутренний интеграл  вычисляется по переменной  при условии, что .
Результат его вычисления зависит от двух переменных  и . Оставшийся после вычисления внутреннего
двойной интеграл вычисляется по проекции параллелепипеда на плоскость .

Этот порядок интегрирования не единственный, так как
существует 6 перестановок из трех элементов   

2.  произвольная правильная область.

Ранее было дано определение правильной области в
системе координат . Аналогично  этому пространственная
область называется правильной, если она правильная в направлениях
осей .    

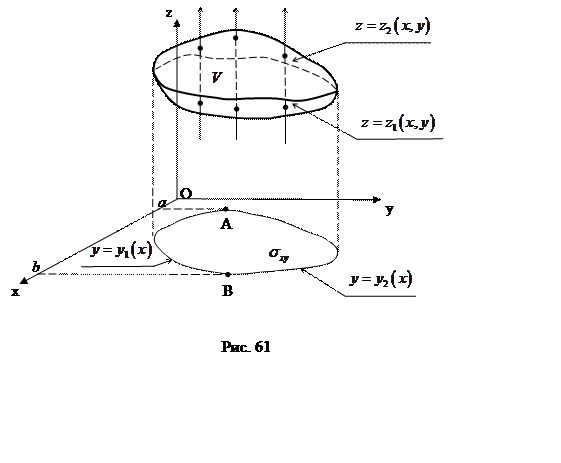Для того чтобы расставить пределы интегрирования в
тройном интеграле, проведем вспомогательные линии, параллельные оси  и проходящие через внутренние точки
области  (рис.61). Все эти линии попадают в область
 на нижней половине поверхности,
ограничивающей область – назовем её поверхностью входа, – а выходят из
области на верхней половине, которая в таком случае является поверхностью
выхода. 

Поэтому 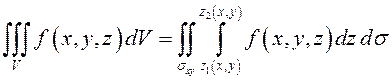, где  – проекция  на
координатную плоскость  (рис.61). Здесь внутренний
интеграл берется по  при фиксированных значениях  и . После
его вычисления остается найти двойной интеграл по плоской области , и окончательный переход от тройного
интеграла к  трехкратному может быть, например, таким:

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Сообщения без ответов | Активные темы

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Площадь части поверхности вырезанной поверхностями в форуме Интегральное исчисление	AnnaV	5	565	02 окт 2016, 08:42
Вычислить площадь части поверхности в форуме Интегральное исчисление	DIOLLlA	16	1465	25 янв 2014, 20:28
Вычислить площадь части поверхности в форуме Интегральное исчисление	patronikus	0	334	14 янв 2016, 18:42
Вычислить площадь части поверхности в форуме Интегральное исчисление	sd2380	11	522	13 сен 2020, 21:04
Вычислить площадь части цилиндрической поверхности в форуме Интегральное исчисление	genia2030	4	801	09 окт 2017, 12:32
Вычислить площадь части поверхности цилиндра в форуме Интегральное исчисление	sapog33	3	1844	03 янв 2017, 14:19
Площадь части поверхности в форуме Интегральное исчисление	Cheesecake	2	278	23 дек 2017, 21:23
Площадь части поверхности в форуме Интегральное исчисление	Olenka_S	1	457	23 апр 2016, 19:22
Найти площадь части поверхности в форуме Интегральное исчисление	firuzinho	7	576	23 дек 2018, 13:14
Найти площадь части поверхности(а) в форуме Интегральное исчисление	keton004	5	195	13 окт 2021, 22:21

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 6

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Вычисление площади поверхности

Пример 1

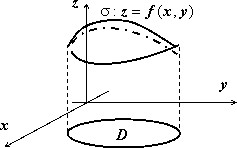
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой

$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $

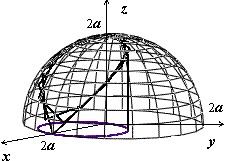
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .

Решение:

На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.

Область $mathbf { textit { D } } $ – сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:

$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.

Пример 2

Вычислить площадь cферы радиуса (a.)

Решение:

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } – { x^2 } – { y^2 } } . } $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$

Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } x } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } y } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { y } { z } . } $

Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $

Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } – { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aintlimits_0^a { frac { { dleft( { { a^2 } – { r^2 } }right) } } { { 2sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aleft. { left( { sqrt { { a^2 } – { r^2 } } }right) }right|_ { r = 0 } ^a } = { – 2pi aleft( { 0 – a }right) = 2pi { a^2 } . } $

Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$