Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
На чтение 6 мин Просмотров 4.3к. Опубликовано 23 мая, 2021
Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Прямоугольник — четырехугольник с разными сторонами у которого все углы по 90о.
Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.
Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Что такое геометрическая фигура
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
За единицу площади взяли квадрат, сторона которого равна единице длины (1 миллиметр, 1 метр, 1 сантиметр). Площадь, которую занимает квадрат со стороной 1 сантиметр назвали квадратный сантиметр (обозначает см2). Если квадрат построен из сторон в 1 м, то его площадь 1 м2. Найти площадь фигуры — значит определить, сколько таких квадратиков можно поместить внутри фигуры.
Расчет площади прямоугольника
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.
В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Как уже говорилось, площадь измеряется в квадратных единицах — метрах, сантиметрах, дециметрах. Результат может быть как целым, так и дробным, например, 4 см2, 6 см2, или 4,6 см2 (4см2 и 6мм2).
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ2
Как она получалась? Начнем с основной формулы S=AB ∙BC. У квадрата АВ=ВС, отсюда S= АВ ∙ АВ = АВ2.
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры:
Содержание
- Как найти площадь круга
- Площадь многоугольника
- Как найти площадь трапеции
- Признаки подобия треугольников
- Параллелепипед
- Шар и сфера, объем шара, площадь сферы, формулы
Как найти площадь круга
Площадь многоугольника
Как найти площадь трапеции
Признаки подобия треугольников
Параллелепипед
Шар и сфера, объем шара, площадь сферы, формулы
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Технологическая карта
урока математики
тема «Площадь прямоугольника»
Учитель: Пикалова И. В.
Класс: 3 Б
Предмет: математика.
Учебник: «Математика 3 класс», часть 1, М. И. Моро, М. А. Бантова
Тип урока: урок открытия новых знаний
Цели: научить детей новым способам нахождения знания, формировать новое понятие, расширить знания учеников за счет включения новых определений.
Задачи:
создать условия для формирования:
положительного отношения к школе и учебной деятельности, интереса к учебному материалу, первичных умений оценки работ, ответов одноклассников (личностные УУД).
Метапредметные:
содействовать формированию у учащихся умений:
принимать и сохранять учебную задачу, соответствующую этапу обучения; определять последовательность промежуточных целей и составлять план и последовательность действий; понимать выделенные учителем ориентиры действия в учебном материале; сличать способ действия и его результат с эталоном; вносить дополнения и корректировать плен и способы действий; оценивать качество и уровень усвоения; способность к волевому усилию. (регулятивные УУД)
формулировать познавательную цель; осуществлять поиск нужной информации; понимать заданный вопрос, в соответствии с ним строить ответ в устной форме; рефлексия способов и условий действия, контроль и оценка процесса и результата деятельности; проводить сравнение изученных объектов по заданным критериям; осуществлять анализ объектов с выделением существенных признаков; устанавливать причинно-следственные связи в изучаемом круге явлений; постановка, формулирование и создание способов решение проблемы. (познавательные УУД)
планировать учебное сотрудничество с учителем и сверстниками; ставить вопросы и разрешать конфликты; управлять поведением партнёра; полно и точно выражать свои мысли, владеть монологической и диалогической формами речи. (коммуникативные УУД)
Предметные задачи: организовать деятельность учащихся по: осмыслению понятия «площадь», умению использовать в речи термины «длина», «ширина», «площадь», умению вычислять площадь прямоугольника.
Оборудование: Компьютер, проектор, электронная презентация, выполненная в программе Power Point, учебники по математике, раздаточный материал.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА МАТЕМАТИКИ
|
Этапы урока |
Деятельность учителя |
Деятельность учащихся |
УУД |
|
Организационный момент Цель этапа: Мотивировать учащихся к учебной деятельности. |
Учитель приветствует учащихся, проверяет их готовность к уроку. С добрым утром, ребята. Желаю вам хорошего настроения и плодотворного урока. А чтобы он был плодотворным, что нам нужно выполнять? |
Приветствуют учителя, проверяют свою готовность к уроку. На уроке не зевать, Время делу посвящать, Если трудности возникли Не сдаваться, а трудиться. |
Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
|
Актуализация знаний Цель этапа: Актуализация опорных знаний и способов действий. |
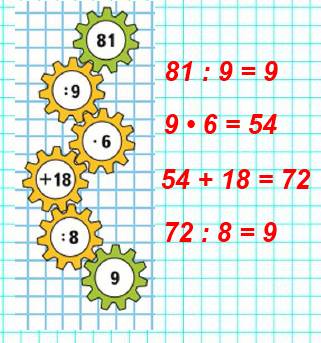
Давайте узнаем название страны, в которую мы отправимся. Для этого вы должны найти значение выражений (ответы записывать в строчку): 5 умножить на 6 (30) 24 разделить на 4 (6) Найдите сумму 11 и 18 (29) Уменьшите 27 в 3 раза.(9) Какое число больше 47 на 6? (53) На сколько 50 меньше 90? (40) I множитель 8,II- 7, найдите произведение.(56) Делимое 49, делитель 7, найдите частное. (7) Увеличьте 7 в 6 раз. (42) Запишите эти числа в порядке возрастания, а под ними соответствующую букву. В стране геометрии живут геометрические фигуры. Что общего у этих фигур? (слайд 3) Среди данных фигур найдите прямоугольники. Докажите свой выбор. Возьмите два прямоугольника и сравните их площади. Какими способами вы пользовались, сравнивая их площади? |
Учащиеся решают примеры устно, ответы записывают в строчку. Проверка каждого ответа. (слайд 2) Проверка. (слайд 2) 6, 7, 9,29, 30, 40, 42, 53, 56 Получилось слово ГЕОМЕТРИЯ. Четырёхугольники. Работа в паре. У учащихся на парте лист с изображением таких же фигур (как и на слайде). Дети, посовещавшись с соседом, отмечают (галочкой) прямоугольники. Проверка. Прямоугольники под номерами 2, 5,6 У этих фигур прямые углы и противоположные стороны равны. Работа в паре. Дети показывают и рассказывают. 1сп.- на глаз; 2 сп.- наложение фигур друг на друга; Вывод: площадь коричневого прямоугольника больше, чем площадь жёлтого. |
Регулятивные: целеполагание, самоконтроль; Коммуникативные: умение выражать свои мысли с достаточной полнотой и точностью, умение слушать понимать речь других. Познавательные: логические анализ объектов с целью выделения признаков. |
|
Выявление причины затруднения Цель этапа: Создание проблемной ситуации. |
Над какой темой продолжаем работать? С каким способом нахождения площади познакомились на прошлом уроке? Начертите в тетради прямоугольник со сторонами 6 см и 3 см, разбейте его на квадратные сантиметры и найдите его площадь. Когда в жизни пригодится умение находить площадь прямоугольника? Удобно ли будет использовать способ разбивки на квадратные сантиметры? Проблема: Как найти площадь прямоугольника, не разбивая каждый раз на квадратные сантиметры? Как вы думаете какова цель нашего урока? |
Площадь прямоугольника. Делением прямоугольника на квадратные сантиметры и подсчёта этих квадратов. Выполнение самостоятельной работы. Проверка. Площадь 18 кв. см. При ремонте (площадь комнаты, потолка, чтобы поклеить обои; пола, чтобы постелить ламинат и т. д.). Нет. Как найти площадь прямоугольника, не разбивая его на квадраты. Цель: вывести формулу нахождения площади прямоугольника и пользоваться ей при решении задач. |
Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение – формулирование познавательной цели, проблемы; логические – формулирование проблемы. Регулятивные: целеполагание. |
|
Построение проекта выхода из затруднения и его реализация Цель этапа: Организация учащихся по исследованию проблемной ситуации; установление осознанности восприятия. |
Площадь прямоугольника 18 кв. см. (слайд 5) Как удобнее и быстрее узнать, сколько всего квадратов в прямоугольнике? Сколько квадратов в каждой полосе? Сколько полос? Значит по 6 квадратов сколько раз взяли? Как записать? Что обозначает число 6 у прямоугольника? А число 3? Сделайте вывод, как найти площадь прямоугольника. Сравните ваш вывод с правилом в учебнике с. 60 Это правило можно записать в виде формулы. Давайте её составим. Площадь в математике принято обозначать буквой S, длину буквой a, ширину – буквой b. (слай 6) Кто может записать формулу? Вот вы и вывели формулу нахождения площади прямоугольника. |
Дети предлагают свои варианты. 6. 3. По 6 3 раза. 6*3=18 кв.см Длина. Ширина. Для нахождения площади прямоугольника надо длину умножить на ширину. Дети читают правило и делают вывод, что они были правы. Ученик на доске пробует записать формулу. Сверяют с записью на слайде. |
Регулятивные: планирование, прогнозирование; Познавательные: моделирование; Логические – решение проблемы, построение логической цепи рассуждений, доказательство; Коммуникативные: инициативное сотрудничество в поиске и выборе информации. |
|
Физминутка |
Раз-подняться, потянуться. Два-нагнуться, разогнуться. Три-в ладоши три хлопка, головою три кивка. На четыре-руки шире. Пять- руками помахать. Шесть- на месте повернуться. Семь- попрыгать, поскакать. Восемь – помолчать. |
Выполняют упражнения |
Усилием воли выполнение задания в соответствии с требованиями. Установка на здоровый образ жизни |
|
Первичное закрепление Цель этапа: Установление правильности и осознанности изучения темы. Выявление первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для сам.работы по новому материалу. |
Организует работу. Задача № 3 (1) с. 61 Начертите этот прямоугольник. Задание 2). |
Выполняют работу. Производят контроль. |
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Познавательные: структурирование знаний, выбор эффективных способов решения задач, рефлексия способов и условий действия, контроль и оценка процесса. Коммуникативные: уметь выражать свои мысли, уметь слушать, вступать в диалог. |
|
Самостоятельная работа с самопроверкой по образцу Цель этапа: Организация деятельности с применением новых знаний |
Людям каких профессий необходимо умение находить площадь фигур? Я предлагаю вам побыть в роли строителей и, работая в паре, из деталей, которые есть у вас на партах, построить дом. Задание.Сделать необходимые измерения и I ряд – найти площадь фундамента. II ряд – найти площадь стены. III ряд – найти площадь окна. |
Строителям, инженерам, конструкторам, архитекторам. Работа в паре. Ученики из фигур выкладывают на парте дом. (слайд 7) Выполняют самостоятельную работу. Измеряют длину и ширину, находят площадь, делая запись в тетрадь. Проверка. (слайд 7) |
Регулятивные: контроль, коррекция, оценка. Личностные: самоопределение. |
|
Информация о домашнем задании, инструктаж по его выполнению. Цель этапа: Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания. |
Дает инструктаж по выполнению домашнего задания. стр. 60 № 2, № 9 (слайд 8) |
Знакомятся с заданием, слушают инструкцию, записывают задание в дневник. |
Коммуникативные: умение слушать. |
|
Рефлексия. Цель этапа: Зафиксировать новое содержание, изученное на уроке. Организовать рефлексию и самооценку учениками собственной учебной деятельности. |
Слайд 9 Задаёт вопросы о достижении цели урока. Побуждает к высказыванию мнения: чему научились? Какую цель ставили в начале урока? Достигли цели? Что нового узнали на уроке? Чему учились на уроке? Как оцениваете свою работу? -если вам было всё понятно, вы легко справлялись с заданиями на уроке, раскрасьте круг синим цветом; – если иногда были трудности, сомнения, то жёлтым; – если вам было трудно выполнять задания, то красным. Оценки. |
Формулируют конечный результат своей работы на уроке. Называют основные позиции нового материала и как они их усвоили. Вывести формулу нахождения площади прямоугольника. Да. Как находить площадь прямоугольника. Решать задачи на нахождение площади прямоугольника. Учащиеся оценивают свою работу на уроке, показывают листы с закрашенным кругом. |
Личностные: умение оценивать себя на основе критерия успешности. Коммуникативные: умение выражать свои мысли с достаточной полнотой и точностью, умение слушать понимать речь других. Познавательные: контроль и оценка процесса и результатов деятельности. |
Страница 60
Будем учиться вычислять площадь прямоугольника.
Надо найти площадь прямоугольника, длины сторон которого 3 см и 4 см. Разделим прямоугольник на квадраты площадью 1 см2 и узнаем, сколько всего таких квадратов в нём уложится. По длине прямоугольника уложилось 4 квадрата площадью 1 см2. Площадь такой полоски 4 см2. При ширине прямоугольника 3 см такая полоска уложится в нём 3 раза. Значит, во всём прямоугольнике уложится 4 • 3=12 квадратов площадью 1 см2.
Ответ: площадь прямоугольника 12 см2.
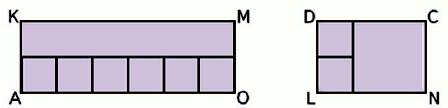
1. Найди площадь каждого прямоугольника.
SAKMO =AK • AO
SAKMO = 2 • 6 = 12 см2
S LDCN =LD • DC
S LDCN =2 • 3 = 6 см2
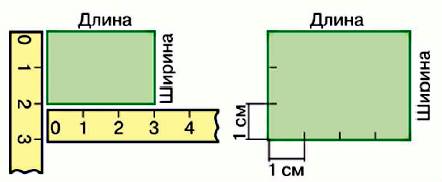
2. Пользуясь рисунком, узнай, площадь какого прямоугольника больше и на сколько квадратных сантиметров.
Решение:
1) 2 • 3 = 6 (см2)− площадь первого прямоугольника;
2) 3 • 4 = 12 (см2)− площадь второго прямоугольника;
3) 12 − 6 = 6 (см2)− площадь второго прямоугольника больше, чем первого.
Ответ: площадь второго прямоугольника больше, чем первого на 6 см2.
Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его: