
{S_{полн}=6a^2}
На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.
В дополнение на сайте можно найти объем куба.
Куб – фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.
Содержание:
- калькулятор площади поверхности куба
- площадь полной поверхности куба
- формула площади полной поверхности куба через ребро
- формула площади полной поверхности куба через диагональ грани
- формула площади полной поверхности куба через диагональ куба
- формула площади полной поверхности куба через периметр грани
- формула площади полной поверхности куба через периметр куба
- формула площади полной поверхности куба через объем
- формула площади полной поверхности куба через площадь вписанного шара
- площадь боковой поверхности куба
- формула площади боковой поверхности куба через ребро
- формула площади боковой поверхности куба через диагональ грани
- формула площади боковой поверхности куба через диагональ куба
- формула площади боковой поверхности куба через периметр грани
- формула площади боковой поверхности куба через периметр куба
- формула площади боковой поверхности куба через объем
- примеры задач
Что такое площадь полной поверхности куба
Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.
Площадь полной поверхности куба – это сумма площадей всех его граней.
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.
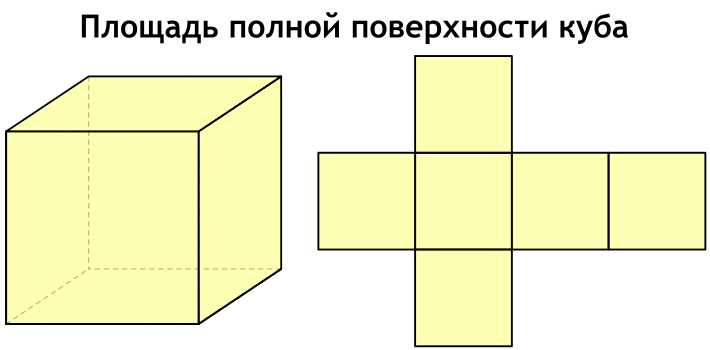
Формула площади полной поверхности куба через ребро
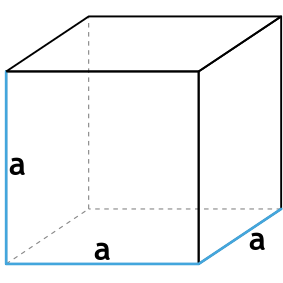
{S_{полн}=6a^2}
a – ребро куба
Формула площади полной поверхности куба через диагональ грани
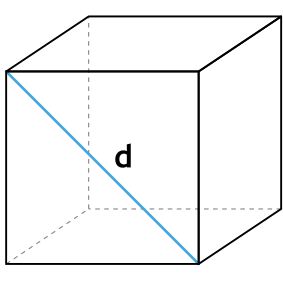
{S_{полн}=3d , ^2}
d – диагональ грани куба
Формула площади полной поверхности куба через диагональ куба
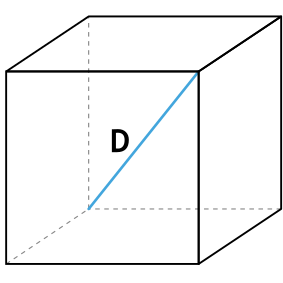
{S_{полн}=2D^2}
D – диагональ куба
Формула площади полной поверхности куба через периметр грани
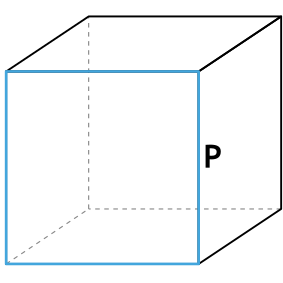
{S_{полн}= dfrac{3}{8}P^2}
P – периметр грани куба
Формула площади полной поверхности куба через периметр куба

{S_{полн}= dfrac{P^2}{24}}
P – периметр куба
Формула площади полной поверхности куба через объем
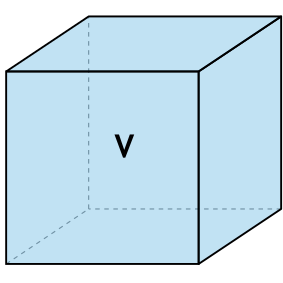
{S_{полн}= 6{(sqrt[3]{V})}^2}
V – объем куба
Формула площади полной поверхности куба через площадь вписанного шара
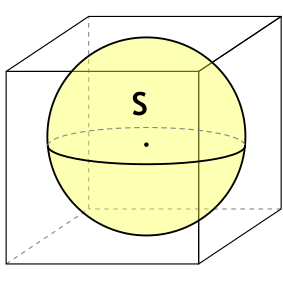
{S_{полн}= 6 dfrac{S}{pi}}
S – площадь вписанного в куб шара
Что такое площадь боковой поверхности куба
Боковая поверхность куба – сумма площадей всех его боковых граней, которых у куба четыре.
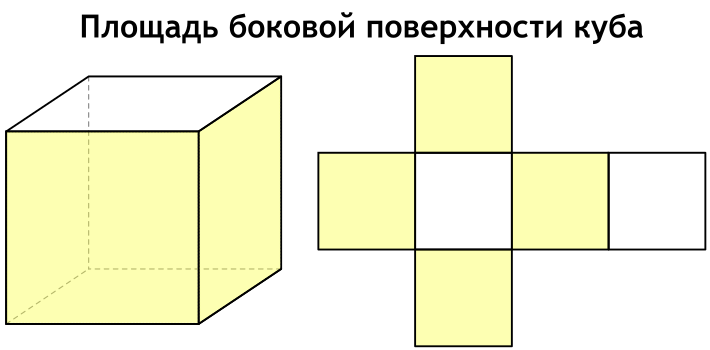
Формула площади боковой поверхности куба через ребро
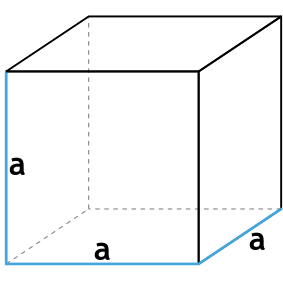
{S_{бок} = 4a^2}
a – ребро куба
Формула площади боковой поверхности куба через диагональ грани
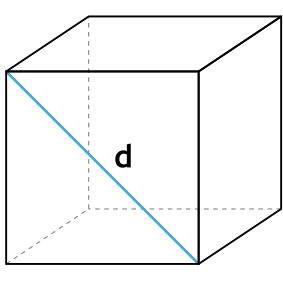
{S_{бок}=2d , ^2}
d – диагональ грани куба
Формула площади боковой поверхности куба через диагональ куба
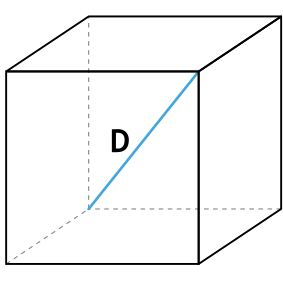
{S_{бок}=dfrac{4}{3}D^2}
D – диагональ куба
Формула площади боковой поверхности куба через периметр грани
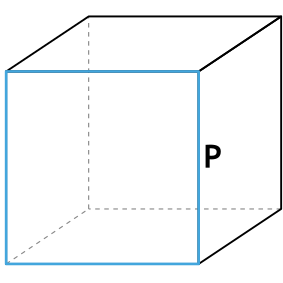
{S_{бок}= dfrac{P^2}{4}}
P – периметр грани куба
Формула площади боковой поверхности куба через периметр куба
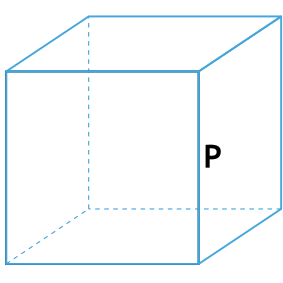
{S_{бок}= dfrac{P^2}{36}}
P – периметр куба
Формула площади боковой поверхности куба через объем

{S_{бок}= 4{(sqrt[3]{V})}^2}
V – объем куба
Примеры задач на нахождение площади поверхности куба
Задача 1
Найдите площадь поверхности куба, если его объем равен 125см³.
Решение
Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.
S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²
Ответ: 150 см²
Проверить ответ нам поможет калькулятор .
Задача 1
Найдите площадь боковой поверхности куба с ребром 4см.
Решение
Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.
S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²
Ответ: 64 см²
Проверка .
ZHAN
Ученик
(142),
закрыт
7 лет назад
фк Краснодар
Мастер
(1558)
7 лет назад
Т. к. по условию периметр одной грани = 32 см, то длина стороны грани = 8 см (потому что грани куба – квадраты) . Отсюда 1)объем будет равен 512 кубических см (8*8*8=512). 2) Площадь одной грани 64 кв. см (т. к. 8*8 = 64), а граней у куба 6, следовательно 64*6=384 кв. см
Ответ: Площадь полной поверхности куба = 384 квадратных см
Объем куба = 512 кубических см
В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
- Примеры задач
Формула вычисления площади куба
1. Через длину ребра
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a2

Данная формула получена следующим образом:
- Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
- Площадь каждой грани считается так: S = a ⋅ a = a2.
- Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√2)2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.
Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)2 = 864 см2.
Задание 2
Площадь поверхности куба равняется 294 см2. Вычислите длину его ребра.
Решение:
Примем ребро куба за a. Из формулы расчета площади следует:![]()
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.
Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)2 = 75 см2.
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Онлайн-калькулятор площади поверхности куба
У куба есть двенадцать ребер, то есть, отрезков, которые являются сторонами квадратов.
Также он имеет восемь вершин и шесть граней.
У куба есть диагональ, соединяющая противоположные вершины.
Формула площади поверхности куба
Площадь поверхности куба – это сумма площадей всех его граней:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Площадь каждой грани одинакова, то есть:
S1=S2=S3=S4=S5=S6=S′S_1=S_2=S_3=S_4=S_5=S_6=S’
S′S’ — площадь любой грани куба.
Тогда полная площадь поверхности куба запишется как:
S=6⋅S′S=6cdot S’
Рассмотрим на примерах разные способы вычисления полной площади поверхности куба.
Формула площади поверхности куба по длине ребра куба
Площадь каждой грани куба вычисляется как площадь квадрата, со стороной ребра куба по формуле:
S′=a⋅a=a2S’=acdot a=a^2
aa — сторона куба.
Отсюда, окончательно площадь поверхности куба:
S=6⋅a2S=6cdot a^2
aa — длина стороны куба.
Найти площадь поверхности куба, если длина его ребра равна 12 (см.).
Решение
a=12a=12
S=6⋅a2=6⋅122=6⋅144=864S=6cdot a^2=6cdot 12^2=6cdot 144=864 (см. кв.)
Ответ: 864 см. кв.
Формула площади поверхности куба по диагонали куба
По теореме Пифагора, диагональ куба связанна с длиной его ребра по формуле:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
d=3⋅ad=sqrt{3}cdot a
Отсюда:
a=d3a=frac{d}{sqrt{3}}
Подставим в формулу для площади:
S=6⋅a2=6⋅(d3)2=2⋅d2S=6cdot a^2=6cdotBig(frac{d}{sqrt{3}}Big)^2=2cdot d^2
S=2⋅d2S=2cdot d^2
dd — диагональ куба.
Одна четвертая часть диагонали куба равна 2 (см.). Найти площадь поверхности куба.
Решение
14⋅d=2frac{1}{4}cdot d=2
Найдем диагональ:
d=4⋅2=8d=4cdot 2=8
Площадь:
S=2⋅d2=2⋅82=2⋅64=128S=2cdot d^2=2cdot 8^2=2cdot 64=128 (см. кв.)
Ответ: 128 см. кв.
Формула площади поверхности куба по длине диагонали квадрата (грани куба)
По теореме Пифагора, диагональ квадрата ll связанна с его стороной aa:
l2=a2+a2l^2=a^2+a^2
l2=2⋅a2l^2=2cdot a^2
l=2⋅al=sqrt{2}cdot a
Тогда сторона квадрата:
a=l2a=frac{l}{sqrt{2}}
Подставляем в формулу для площади и получаем:
S=6⋅a2=3⋅l2S=6cdot a^2=3cdot l^2
S=3⋅l2S=3cdot l^2
ll — диагональ квадрата (грани куба).
Одна четвертая часть диагонали квадрата равна 1 (см). Найти площадь поверхности куба, образованного данным четырехугольником.
Решение
14⋅l=1frac{1}{4}cdot l=1
Найдем диагональ квадрата:
l=4⋅1=4l=4cdot 1=4
Тогда площадь:
S=3⋅l2=3⋅42=48S=3cdot l^2=3cdot 4^2=48 (см. кв.)
Ответ: 48 см. кв.
Разберем более сложные примеры.
Формула площади поверхности куба по площади вписанного в куб шара
В куб вписан шар площади SшарS_{text{шар}}. Тогда радиус RR этого шара равен половине длины стороны куба aa:
R=a2R=frac{a}{2}
Площадь шара дается формулой:
Sшар=4⋅π⋅R2S_{text{шар}}=4cdotpicdot R^2
Отсюда найдем радиус шара:
R=Sшар4⋅πR=sqrt{frac{S_{text{шар}}}{4cdotpi}}
Сторона грани куба:
a=2⋅R=2⋅Sшар4⋅πa=2cdot R=2cdotsqrt{frac{S_{text{шар}}}{4cdotpi}}
Наконец площадь поверхности куба:
S=6⋅a2=6⋅SшарπS=6cdot a^2=frac{6cdot S_{text{шар}}}{pi}
S=6⋅SшарπS=frac{6cdot S_{text{шар}}}{pi}
SшарS_{text{шар}} — площадь шара, вписанного в куб.
В куб вписан шар, площадь которого равна 64 “пи” (см. кв.). Найти полную площадь поверхности куба.
Решение
Sшар=64πS_{text{шар}}=64pi
По формуле:
S=6⋅Sшарπ=6⋅64⋅ππ=384S=frac{6cdot S_{text{шар}}}{pi}=frac{6cdot 64cdotpi}{pi}=384 (см. кв.)
Ответ: 384 см. кв.
Не знаете, кто сможет решить контрольную работу на заказ для вас? Наши эксперты с удовольствием окажут вам помощь!
Тест по теме “Площадь поверхности куба”
Площадь куба, она же площадь полной поверхности куба, равна увеличенной в шесть раз площади одной его грани. Так как площадь куба зависит только от ребра, зная ее, можно легко вычислить ребро и затем все остальные параметры куба.
S_(п.п.)=6a^2
a=√(S_(п.п.)/6)
Соответственно, площадь стороны куба – одной его грани, будет равна площади полной поверхности разделенной на шесть, а площадь боковой поверхности, состоящей из четырех граней, – двум третям площади полной поверхности куба.
S=S_(п.п.)/6
S_(б.п.)=2/3 S_(п.п.)
Для того чтобы найти объем куба, необходимо его ребро возвести в третью степень. Используя полученную формулу ребра куба через площадь полной поверхности, получим, что объем куба равен одной шестой квадратного корня из площади куба в третьей степени, деленной на шесть.
V=a^3=(√(S_(п.п.)/6))^3=1/6 √(〖S_(п.п.)〗^3/6)
Периметр куба можно найти, умножив ребро куба на 12. Если подставить вместо ребра квадратный корень через площадь куба, то получим следующую формулу для периметра куба:
P=12a=12√(S_(п.п.)/6)
Диагональ одной стороны куба является по определению диагональю квадрата, которая вычисляется как произведение стороны квадрата на корень из двух. Так как ребро куба является стороной этого квадрата, то диагональ будет равна квадратному корню из площади, деленной на 3.
d=a√2=√(S_(п.п.)/3)
Чтобы рассчитать диагональ куба, необходимо провести дополнительное построение на чертеже, соединяющее ребро куба и одну из вершин диагонали в прямоугольный треугольник. Это дает возможность воспользоваться теоремой Пифагора и вычислить диагональ куба через площадь, подставив формулу вместо ребра куба. (рис.2.1)
a^2+d^2=D^2
D^2=a^2+2a^2
D^2=3a^2
D=a√3=√(S_(п.п.)/2)
Радиус сферы, вписанной в куб, по определению равен половине ребра куба или половине квадратного корня из площади куба, деленной на шесть. (рис. 2.2)
r=a/2=1/2 √(S_(п.п.)/6)
Радиус сферы, описанной вокруг куба, представлен половиной диагонали куба, которая равна площади полной поверхности куба, деленной на два, под корнем. (рис.2.3)
R=D/2=1/2 √(S_(п.п.)/6)
