1) Закрашенная часть квадрата тоже квадрат (рис.7.35). Убедитесь в этом, выполнив необходимые измерения. Во сколько раз площадь закрашенного квадрата меньше площади большего квадрата?
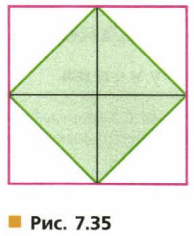
Подсказка. Скопируйте рисунок на лист бумаги в клетку, вырежьте квадрат и перегните прямоугольные треугольники к центру по сторонам закрашенного квадрата.
2) Площадь красного квадрата (рис.7.36) равна 1 кв.ед. Чему равна площадь черного квадрата?
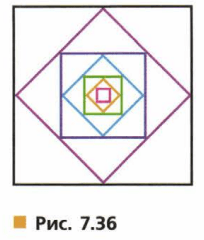
3) Пусть площадь черного квадрата (см.рис.7.36) равна 2 кв.ед. Начертите квадрат, площадь которого равна 8 кв.ед.

reshalka.com
Математика 5 класс Дорофеев. 7.4 Площадь прямоугольника. Номер №598
Решение 1
Из зеленых треугольников на рисунке 7.35 можно составить следующий прямоугольник.
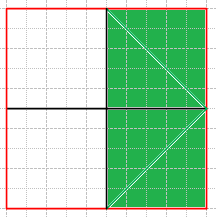
Отсюда видно, что площадь красного квадрата в 2 раза больше площади зеленого.
Решение 2
1) 1 * 2 = 2 (кв.ед.) − площадь желтого квадрата;
2) 2 * 2 = 4 (кв.ед.) − площадь зеленого квадрата;
3) 4 * 2 = 8 (кв.ед.) − площадь голубого квадрата;
4) 8 * 2 = 16 (кв.ед.) − площадь синего квадрата;
5) 16 * 2 = 32 (кв.ед.) − площадь фиолетового квадрата;
6) 32 * 2 = 64 (кв.ед.) − площадь черного квадрата.
Ответ: 64 кв.ед.
Решение 3

1) 2 * 2 = 4 (кв.ед.) − площадь зеленого квадрата;
2) 4 * 2 = 8 (кв.ед.) − площадь красного квадрата.
$begingroup$

The graph of $y=sqrt{3}x$ and its inverse and the line $x=4$ is given.
I have restarted a course on functions and graphs. I managed to find the point of intersection between the green line and the blue line as $(4, frac{4}{sqrt{3}})$. I have been trying to find the other point on the blue line and till now I have only been able to estimate that it is ~$2.5$(picture is drawn to scale that’s why) but that’s probably an unreasonable approach as I am expected to give an exact value. How would one find the other end of the side of the black square on the blue line without its distance?
asked Sep 11, 2022 at 11:37
$endgroup$
$begingroup$
Let$$A=left(a,frac a{sqrt3}right)$$be an arbitrary point of the blue line and let$$B=left(4,frac 4{sqrt3}right).$$Then the straight line orthogonal to the blue line passing through $A$ is the line $y=-sqrt3(x-a)+frac a{sqrt3}$. This line intersects the red line at$$C=left(frac{2a}3,frac{2a}{sqrt3}right).$$What remains to be determined are the values of $a$ for which the distance from $A$ to $B$ is equal to the distance from $A$ to $C$. That happens when and only when $a=6pm2sqrt3$. See the picture below:

Numerically, the values of $a$ mentioned above are about $2.54$ and $9.46$.
Of course, if we add the assumption that the square is not cut by the red line, then the only valid solution is the one for which $a=6-2sqrt3$, in which case the area of the square is equal to $frac{32}3left(2-sqrt3right)$.
answered Sep 11, 2022 at 11:58
![]()
$endgroup$
2
$begingroup$
Since the two lines are invers of each other and the slopes of them make $30°$ with the axis, the area of the square can be easily calculated by using Pythagoras.

answered Sep 18, 2022 at 12:25
![]()
SeyedSeyed
8,8084 gold badges20 silver badges30 bronze badges
$endgroup$
$begingroup$
As the angle that $y = sqrt3 x$ makes with the $x$-axis is $60º$, its inverse makes an angle of $30º$ so the angle between these two lines is $30º$. Also, $sqrt{4^2 + (4/sqrt3)^2} = 8/sqrt{3}$, so we have:

and thus:
$$frac{BC}{sin 30º} = frac{8/sqrt3}{sin 105º} implies BC = frac{4}{sqrt3 left( frac{sqrt 2}{2} cdot frac{sqrt3}{2} + frac{sqrt 2}{2} cdot frac{1}{2} right)} =frac{4}{frac{3 sqrt 2}{4} + frac{sqrt 6}{4}}$$
$$ = frac{16}{3 sqrt2 + sqrt{6}}$$
Now as $BC = sqrt{2}( text{side length})$, the area of the square is $BC^2/2$ or just:
$$frac{1}{2} frac{256}{18 + 6 + 6 sqrt{12}} = frac{128}{24 + 12 sqrt{3}} = frac{32}{6 + 3 sqrt3}.$$
answered Sep 18, 2022 at 12:56
Toby MakToby Mak
16.7k4 gold badges25 silver badges46 bronze badges
$endgroup$
1
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Как найти отношение закрашенной площади к не закрашенной?
Интересная задача, которая мне попалась на глаза- найти отношение закрашенной области черным к закрашенной белым.
Вот у нас такая картинка:

Решение задачи соотношение закрашенных частей
1.
Если мы возьмем за начало отсчета первый самый маленький квадрат, который стоит внутри – это белый квадрат, то описанный вокруг белого, первый черный квадрат относится к нашему белому квадрату как 2 к 1
Докажем это самым простым визуальным способом:
Разделим наш квадрат пополам и получим вот такую картинку, из которой мы видим, что белый квадрат состоит из 4 одинаковых треугольников, в черный квадрат состоит из одинаковых 8 треугольников 8 относится к 4, как 2 к 1. Думаю математически это не нужно доказывать!?

Из верхнего мы имеем, что площадь черного и белого равны друг другу!
У нас получится 1 единица белого и 1 единица черного…
2.
Теперь, если мы проделаем это с большой картинкой. То логика сразу будет понятна!
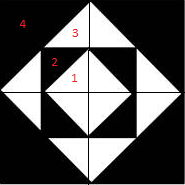
Теперь нам нужно определить соотношение черных треугольников 2 к белым треугольникам 3, из той же логики мы видим, что они носятся к друг другу как как 8 к 4, т.е. в два раза больше, из первого пункта мы вывели, что и черных и белых по единице, если мы умножим единицу на 2, то получим 2 единицы белого
3.
По той же логике мы здесь видим, что треугольник №2 относится к треугольнику №4, как 16 к 4, или 4 к 1, другими словами площадь большой площади квадрата №4 – равно 4 единицам.
Итого:
1 единица черного(№2) + 4 единицы(№4) черного = 5
1 единица белого(№1) + 2 единицы(№3) белого = 3
Площадь черного и белого относится как 5 : 3
Написать что-нибудь…
Квадрат — правильный четырехугольник, у которого все стороны и углы равны. Это идеальная геометрическая фигура, которая широко встречается в реальности и имеет большое прикладное значение.
Геометрия квадрата
Квадрат — четыре точки, четыре стороны, четыре прямых угла. Диагонали четырехугольника равны, пересекаются под углом 90 градусов, в точке пересечения делятся пополам и являются биссектрисами углов фигуры. Кроме того, диагонали разделяют фигуру на равнобедренные прямоугольные треугольники, что делает квадрат королем симметрии. Квадрат — частный случай параллелограмма, ромба и прямоугольника.
В евклидовой геометрии все углы квадрата равны 90 градусам, а сумма углов фигуры составляет 360 градусов. Евклидова геометрия — это теория о фигурах, построенных на плоскости. Если квадрат построить на сфере, то каждый его угол будет равен 120 градусам, а если на гиперболической поверхности — 72 градуса. Таким образом, в геометриях Римана и Лобачевского квадрат, как фигура с прямыми углами, не существует, и представляет собой равносторонний четырехугольник.
Единичный квадрат
Единичный квадрат — это плоский квадрат, сторона которого равна единичному отрезку. Такой четырехугольник используется для измерения площади других геометрических фигур: измерение размеров сводится к задаче вычисления количества единичных квадратов, которые могут замостить плоскость, ограниченную сторонами фигуры. Известно, что такой метод определения площадей использовали древние вавилоняне, а вот отец геометрии Евклид замерял фигуры относительно друг друга. До открытия интегрального исчисления нахождение площади фигур при помощи единичного квадрата называлось квадратурой.
Квадрат в реальности
Квадрат — двухмерная вариация куба, и квадратную форму имеет множество реальных объектов. Помимо того, что квадраты постоянно встречаются при вычислениях площадей, форму квадрата имеют тротуарные плитки, ковры, флаги, а также грани сахарных кубиков, ламповых телевизоров или картонных ящиков. Абстрактный четырехугольник широко распространен в дизайне, архитектуре и искусстве, а самым известным квадратом в мире считается «Черный квадрат» Казимира Малевича.
Площадь квадрата
Формула площади квадрата — одна из самых простых формул, которые мы знаем со школьной скамьи. Для вычисления нам необходимо возвести в квадрат сторону фигуры:
S = a2.
В школьных задачах может потребоваться отыскать размер квадрата, зная только его диагональ. Программный код калькулятора использует известную зависимость между стороной и диагональю квадрата, которая выводится из теоремы Пифагора. Так как диагонали разделяют квадрат на равнобедренные прямоугольные треугольники, то их катеты равны, поэтому:
d2 = a2 + a2
Для единичного квадрата диагональ соотносится со стороной как d = 1,4142a. Вы можете вычислить площадь фигуры, зная только одну переменную на выбор:
- длину стороны;
- длину диагонали.
Рассмотрим пару примеров.
Примеры из реальной жизни
Кафель
Допустим, мы хотим отделать стену кафелем. Чаще всего кафель имеет именно квадратную форму, и для того чтобы выяснить расход отделочного материала, нам понадобится узнать площадь поверхности и размер одного элемента. Пусть нам требуется замостить кафелем пол в ванной комнате, площадь которого составляет 3 квадратных метра, а для отделки мы выбрали кафельные плитки со стороной 15 см. Для корректного расчета представим сторону в метрах, то есть a = 0,15. Площадь одной плитки составит:
S = 0,0225.
Тогда для отделки пола нам понадобится 3/0,0225 = 133 кафельных плитки.
Школьная задача
В задаче по геометрии требуется определить площадь квадрата, длина диагонали которого составляет 13 см. При решении такой задачи вручную нам потребовалось бы использовать теорему Пифагора для вычисления стороны. Мы можем сэкономить время и просто ввести длину диагонали в форму калькулятора и получить ответ, равный:
S = 84,5
Сторона квадрата при этом равна 9,19 см, что соответствует теореме Пифагора. Так как все стороны квадрата равны, мы не можем получить пифагоровы тройки (то есть натуральные числа) при вычислении параметров фигуры.
Заключение
Квадрат — популярный четырехугольник. Расчет площади квадрата понадобится не только школьникам, но и представителям различных профессий. Несмотря на то, что формула для вычисления площади проста до безобразия, вам может понадобиться помощь при расчетах периметров и площадей других многоугольников. Для более сложных задач используйте калькуляторы из нашего каталога — там вы найдете инструменты для решения самых разных математических вопросов.
Эту задачу я нашел на канале MathBrain. Дал своим ученикам, двое решили за минуту, остальные думали дольше, но решили все.
Задача чисто геометрическая – надо найти площадь большого квадрата, если известна площадь маленького красного треугольника.
Не устаю говорить, что геометрические задачи хороши тем, что они отлично развивают пространственное мышление и логику, умение находить разные способы решения и решать не по алгоритму, как в алгебре и во многих других дисциплинах. Так что, если не хотите, чтобы или ваше дети были полуроботами, которые могут работать только по алгоритму [а ещё говорят, что такими людьми легко управлять], решайте геометрические задачки.
Тут есть два способа решения. Один строгий, через уравнения, как многие любят. Другой красивый, вообще без формул.
Начну с первого, строгого. Для этого давайте обозначим половину стороны большого квадрата за Y, а катет красного треугольника за X. Надеюсь, что никому не нужно доказывать, что треугольник красный треугольник прямоугольный?! На всякий случай вот поясняющий рисунок.
Рассматриваем левый верхний треугольник: у него два катета равны Y, а гипотенуза 2X. По теореме Пифагора (2Х)²=2Y²; 4Х²=2Y²; 2Х²=Y².
Площадь большого квадрата можно записать как 4Y²=8X². Осталось найти Х. Это легко сделать с помощью красного треугольника с известной площадью. S=½X²=1 следовательно X²=2. подставляем в площадь большого квадрата и получаем 8X²=8·2=16.
***
Теперь второй способ. Дорисуем диагонали большого квадрата. Таким образом он поделится на 16 равных прямоугольных треугольников равных красному. Стало быть площадь большого квадрата – это 16 площадей красного треугольника, то есть 16.
Какое решение вам больше понравилось? И как решили вы?
Ещё интересно: Математики всего мира не могут договориться, о том, какой ответ считать правильным: 9 или 1
Олимпиадная задача для 8 класса, которая решается устно
