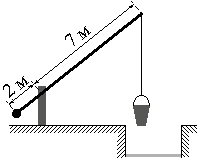|
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Задача решается очень просто, если использовать теорему об отношении площадей подобных фигур. В данной задаче подобными являются треугольники АВС и CNM, так как средняя линия NM параллельна основанию АВ. Коэффициент подобия к=АВ/NM = 2. По теореме об отношении площадей подобных фигур площади треугольников АВС и CNM относятся как к^2, то есть Sabc/Snmc = k^2 = 4. Значит площадь треугольника АВС Sabc = 4*Snmc = 4*57 = 228. Ответ: 228. система выбрала этот ответ лучшим
Евгений трохов 3 года назад S1 треугольника CNM=57= =CN*NM*sin CNM*1/2 S2 треугольника АВС=АВ*АС *(1/2)*sin CAB Sin CAB=sin CMN S2/S1=AB*AC/CN*NM=2*2=4 4S1=S2 S2=57*4=228 S ANMB=S2-S1=228-57=171 Ответ: площадь искомого четырехугольника равна 171. Знаете ответ? |
Задания
Версия для печати и копирования в MS Word
Тип 17 № 352922 
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 12. Найдите площадь четырёхугольника ABMN.
Спрятать решение
Решение.
MN − средняя линия треугольника ABC. Треугольники ABC и NMC подобны по двум углам. Коэффициент подобия k = 2. Значит, 
а 
Ответ: 36.
Аналоги к заданию № 323774: 341524 339694 341357 … Все
Спрятать решение
·
Прототип задания
·
Помощь
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | диагональ и угол между ними | |
|
| 2 | стороны и углы между этими сторонами | |
|
| 3 | стороны (по Формуле Брахмагупты) |
|
|
| 4 | стороны и радиус вписанной окружности | |
|
| 5 | стороны и углы между ними | |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Как найти площадь четырехугольника abmn
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Это задание ещё не решено, приводим решение прототипа.
В треугольнике A B C отмечены середины M и N сторон B C и A C соответственно. Площадь треугольника C N M равна 12. Найдите площадь четырёхугольника A B M N .
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
[spoiler title=”источники:”]
http://oge.sdamgia.ru/problem?id=339511
http://www.mozgan.ru/Geometry/ArearQuadrangle
[/spoiler]
griprororeh483
Вопрос по геометрии:
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 12. Найдите площадь четырёхугольника ABMN.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
unthosai59
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 12. Найдите площадь четырёхугольника ABMN .
————————————-
NM | | AB ; NM =AB/2 ( Свойство средней линии треугольника ).
S(ACB)/S(NCB) =(AB/NM)² * * * ΔACB ∞ ΔNCB * * *
S(ACB)/12 =4 ;
S(ACB) = 48.
S(ABMN) = S(ACB) – S(NCB) =48 -12 = 36.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Задача №365 из 1087
|
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Решение задачи:
Вариант №1
MN –
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
Проведем
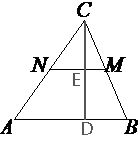
высоту из вершины С.
SCNM=1/2*CE*NM=57 (по условию).
CE*NM=114
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE –
средняя линия для треугольника ACD, значит CE=ED.
ABMN – трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*114=171
Ответ: SABMN=171
Вариант №2 (Прислал пользователь Артем)
MN –
средняя линия треугольника ABC, по теореме о средней линии MN=AF=FB.
Проведем два отрезка от середины AB к точкам N и M, как показано на рисунке.
FN и FM – тоже являются
средними линиями, следовательно:
FN=CM=BM и FM=AN=CN
Заметим, что треугольники ANF, CNM, MBF и NMF равны друг другу по
третьему признаку равенства треугольников.
SABNM=SANF+SNMF+SMBF=SCNM+SCNM+SCNM=3*SCNM=3*57=171
SABNM=171
Вы можете поблагодарить автора, написать свои претензии или предложения на
странице ‘Про нас’
Другие задачи из этого раздела
Задача №0DD35B
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Задача №81E850
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Задача №005D56
Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Задача №B96811
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
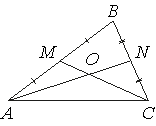
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
