Как найти площадь четырехугольника для 4 класса – Сайт, где вы сможете решить свои вопросы

Калькулятор расчета площади четырехугольника

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

Формулы вычисления площади произвольного четырёхугольника

В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
Угол между сторонами a и b будем обозначать следующей записью (a,b).

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Заключение

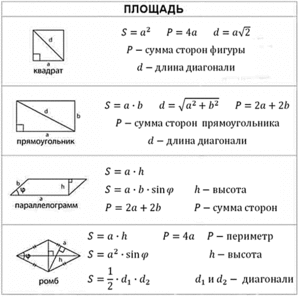
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

S = 1/2*d1*d2*sin(d1,d2);
S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.

Видео

Разобраться в этой теме вам поможет видео.

Площадь неправильного четырехугольника

Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.

С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».

Как найти площадь неправильного четырехугольника?

Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.

Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

где d₁, d₂ — диагонали четырехугольника, α — острый угол между диагоналями .

[spoiler title=”источники:”]

http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika

http://kalk.pro/math/area/ploshad-nepravilnogo-chetyrehugolnika/

[/spoiler]

Источник

Загрузить PDF

Вам дана задача, в которой требуется найти площадь четырехугольника, а вы даже не знаете, что такое четырехугольник? Не волнуйтесь, эта статья вам поможет! Четырехугольник — это любая фигура с четырьмя сторонами. Для вычисления площади четырехугольника нужно определить тип четырехугольника, который вам дан, и воспользоваться соответствующей формулой.

1
Определение параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны равны и параллельны друг другу. Квадраты, прямоугольники и ромбы — это параллелограммы.
- Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
- Ромб — это параллелограмм, у которого все стороны равны.
2
Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона; представьте ее как высоту) и длину (длинная сторона; представьте ее как сторону, к которой проведена высота). Площадь прямоугольника равна произведению длины на ширину.
- ‘Площадь = длина х высота, или S = a х h.
- Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
- Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).
3
Площадь квадрата. Квадрат — это частный случай прямоугольника, поэтому используйте ту же формулу, что и для нахождения площади прямоугольника. Но в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (то есть умноженной саму на себя).^[1]
- Площадь = сторона х сторона, или S = a².
- Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a² = 4 х 4 = 16 квадратных сантиметров.
4
Площадь ромба равна произведению его диагоналей, разделенной на два. Диагонали — это отрезки, соединяющие противоположные вершины ромба.^[2]
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.
5
Площадь ромба также можно найти, если умножить его сторону на высоту, опущенную на эту сторону. Но не путайте высоту со смежной стороной. Высота — это прямая, опущенная из любой вершины ромба на противоположную сторону, и пересекающая противоположную сторону под прямым углом.
- Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.
6
Формулы для вычисления площадей ромба и прямоугольника применимы к квадратам, так как квадрат — это частный случай как прямоугольника, так и ромба.
- Площадь = сторона х высоту, или S = a × h
- Площадь = (диагональ1 × диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
- Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.
Реклама

1
Определение трапеции. Трапеция — это четырехугольник, у которого две противоположные стороны параллельны друг другу. Каждая из четырех сторон трапеции может быть разной длины.
- Есть два способа вычисления площади трапеции (в зависимости от данных значений).
2
Найдите высоту трапеции. Высота трапеции — отрезок, соединяющий параллельные стороны (основания) и пересекающий их под прямым углом (высота не равна боковым сторонам). Вот как найти высоту трапеции:^[3]
- Из точки пересечения меньшего основания и боковой стороны проведите перпендикуляр к большему основанию. Этот перпендикуляр и есть высота трапеции.
- Чтобы вычислить высоту, используйте тригонометрию. Например, если вы знаете боковую сторону и прилегающий к ней угол, то высота равна произведению боковой стороны на синус прилегающего угла.
3
Найдите площадь трапеции, используя высоту. Если вы знаете высоту трапеции и оба основания, используйте следующую формулу для вычисления площади трапеции:
- Площадь = (основание1 + основание2)/2 × высота, или S = (a+b)/2 × h
- Пример: если высота трапеции равна 2 см, а основания трапеции равны 7 см и 11 см, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 11)/2 * 2 = 18 квадратных сантиметров.
- Если высота трапеции равна 10, а основания трапеции равны 7 и 9, то площадь этой трапеции: S = (a+b)/2 * h = (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80.
4
Найдите площадь трапеции, используя среднюю линию. Средняя линия — это отрезок, параллельный основаниям и делящий боковые стороны пополам. Средняя линия равна среднему значению от обоих оснований (a и b): средняя линия = (a+b)/2.
- Площадь = средняя линия х высота, или S = m × h
- По сути, здесь вы используете формулу для нахождения площади трапеции по двум основаниям, но вместо (a+b)/2 подставлена m (средняя линия).
- Пример: если средняя линия трапеции равна 9 см, то площадь этой трапеции: S = m*h = 9 х 2 = 18 квадратных сантиметров (вы получили тот же ответ, что и в предыдущем шаге).
Реклама

1
Определение дельтоида. Дельтоид — это четырехугольник с двумя парами сторон одинаковой длины.
- Есть два способа вычисления площади дельтоида (в зависимости от данных значений).
2
Найдите площадь дельтоида, используя формулу для нахождения площади ромба (с использованием диагоналей), так как ромб — это частный случай дельтоида, у которого все стороны равны. Напомним, что диагональ — отрезок, соединяющий противоположные вершины.
- Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
- Пример: если диагонали дельтоида равны 19 см и 5 см, то площадь этого дельтоида: S = (19 х 5)/2 = 47,5 квадратных сантиметров.
- Если вы не знаете длины диагоналей и не можете их измерить, используйте тригонометрию, чтобы вычислить их. Прочтите эту статью, чтобы узнать больше информации.
3
Найдите площадь дельтоида, используя неравные стороны и угол между ними. Если вы знаете неравные стороны и угол между этими сторонами (θ), то площадь дельтоида вычисляется с помощью тригонометрии по формуле:^[4]
- Площадь = (сторона1 х сторона2) х sin (угол), или S = (a × b) × sin(θ), где θ — угол между неравными сторонами.
- Пример: Если стороны дельтоида равны 4 см и 6 см, а угол между ними равен 120 градусам, то площадь дельтоида равна (6 х 4) х sin120 = 24 х 0,866 = 20,78 квадратных сантиметров.
- Обратите внимание, что вы должны использовать две неравные стороны и угол между ними; если вы используете две равные стороны и угол между ними, вы получите неправильный ответ.
Реклама

1
Если вам дан четырехугольник произвольной формы, то даже для таких четырехугольников существуют формулы для вычисления их площадей. Обратите внимание, что такие формулы требуют знания тригонометрии.
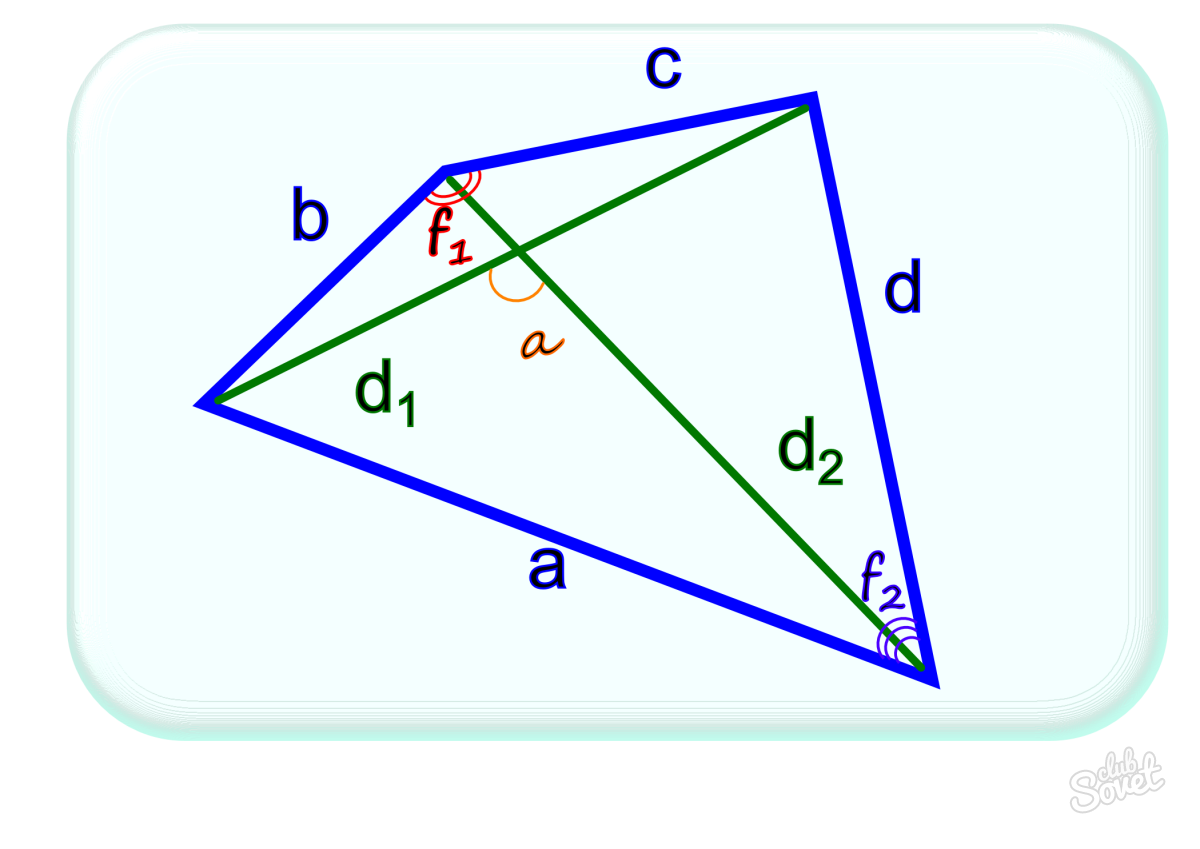
- Во-первых, найдите длины всех четырех сторон. Обозначим их через a, b, c, d (а напротив с, а b напротив d).
- Пример: дан четырехугольник произвольной формы со сторонами 12 см, 9 см, 5 см и 14 см.
2
Найдите угол А между сторонами а и d и угол С между сторонами b и с (вы можете найти любые два противолежащих угла).
- Пример: в нашем четырехугольнике А = 80 градусов и C = 110 градусов.
3
Представьте, что существует отрезок, соединяющий вершины, образованные сторонами а и b и сторонами с и d. Этот отрезок разделит четырехугольник на два треугольника. Так как площадь треугольника равна 1/2absinC, где C — угол между сторонами a и b, вы можете найти площади двух треугольников и сложить их, чтобы вычислить площадь квадрата.
- Площадь = 0,5 х сторона1 х сторона4 х sin(угол между стороной1 и стороной4) + 0,5 х сторона2 х сторона3 х sin(угол между стороной2 и стороной3), или
- Площадь = 0,5 a × d × sin A + 0,5 × b × c × sin C
- Пример: вы нашли стороны и углы, поэтому просто подставьте их в формулу.
  
  = 0,5 (12 × 14) × sin (80) + 0,5 × (9 × 5) × sin (110)
  
  = 84 × sin (80) + 22,5 × sin (110)
  
  = 84 × 0,984 + 22,5 × 0,939
  
  = 82,66 + 21,13 = 103,79 квадратных сантиметров.
- Обратите внимание, что если вы пытаетесь найти площадь параллелограмма (у которого противоположные углы равны), то формула примет вид: площадь = 0.5*(ad + bc) * sin A
Реклама

Советы

Этот калькулятор для вычисления площади треугольника пригодится вам при вычислении площади четырехугольника произвольной формы.^[5]
Чтобы получить дополнительную информацию, прочитайте статьи по вычислению площади квадрата, площади прямоугольника, площади ромба, площади трапеции и площади дельтоида.

Об этой статье

Эту страницу просматривали 440 069 раз.

Была ли эта статья полезной?

Источник

Находить площадь фигуры можно не только по формулам, но чаще всего мы используем именно их. Первые формулы площади нам дают в 3 – 4 классах и это четырёхугольники – прямоугольник и квадрат. К сожалению, некоторые и эти формулы к экзамену не знают. Ну а мы рассмотрим задачу для решения которой будем использовать ещё более сложную формулу. Формулу площади произвольного (т.е. любого) четырёхугольника. Начнём?

Условие

Рис. 1. С.А. Шестаков, «Сборник задач. 9 класс»

Рассуждение

В условии ни слова не сказано про диагонали;
Точки M, F и K – середины сторон AB, AD и DC, а значит если их соединить, тополучатся отрезки соединяющие середины сторон (масло масляное);
Отрезки FM и KF – известны, угол между ними ∠MFK – тоже, и это похоже на теорему косинусов, но MK – кажется бесполезным в решении отрезком.

Решение

Нарисуем произвольный четырёхугольник, то есть так, чтоб он не был похож ни на параллелограммы, ни на трапеции. И отметим середины сторон, известные отрезки и угол:

Рис. 2. ABCD – четырёхугольник; точки M, F и K – середины сторон AB, AD и DC

Отрезки MF и FK – соединяют середины сторон, что очень напоминает средние линии. Рассмотреть их помогут диагонали.

Рис. 3. BD и AC – диагонали четырёхугольника; точка E – точка пересечения диагоналей

Теперь видно, что MF – средняя линия в ∆ABD, а FK – в ∆ACD.

Рассмотрим ∆ABD:

Рис. 4. MF – средняя линия в треугольнике ∆ABD

По свойству средне линии треугольника (равна половине параллельной ей стороны), можно найти диагональ BD, будет в 2 раза больше MF:

BD = 12√3 см.

Аналогично найдём диагональ AC через ∆ACD:

AC = 20 см.

Теперь нам известны обе диагонали найдём угол между ними. Для этого рассмотрим четырёхугольник NEHF:

Рис. 5. NEHF – параллелограмм

Опять по свойству средней линий треугольника (только теперь параллельность стороне), определим тип четырёхугольника:

NEHF – параллелограмм ( противолежащие стороны параллельны).

Осталось найти площадь по формуле:

Рис. 6. Формула площади произвольного четырёхугольника через диагонали

Подставим в формулу найденные диагонали и синус 120° (равен синусу 60°) и получим ответ.

Ответ: 180

Заключение

В этом решении мы применяли:

Свойства средней линии треугольника.
Формула площади произвольного четырёхугольника через диагонали и угол между ними.

Применение

Понять, что Вам нужна именно эта формула площади обычно проще, чем в рассмотренной задаче. Вам будут давать длины диагоналей или угол между ними, а найти нужно будет площадь. Могут наоборот дать площадь и попросить узнать диагональ или угол между ними. Формула встречается в первой части ОГЭ: ссылка на задания из открытого банка заданий ОГЭ.

Попробуйте решить и похожую на ту, что мы разобрали:

Рис. 7. С.А. Шестаков, «Сборник задач. 9 класс»

Пробуйте, решайте, изучайте, делитесь решениями в комментариях. Удачи!

Источник

Голосование за лучший ответ

наталия стафеева

Профи

(820)

13 лет назад

все стороны сложить!

Евгения Гордеева

Мыслитель

(7624)

13 лет назад

Ширину умножить на длину:)

zzz

Мастер

(1830)

13 лет назад

Загляни в учебник, там тоже много чего познавательного есть…

Лёлик

Профи

(583)

13 лет назад

перемножить все стороны

Елизавета Власова

Профи

(822)

13 лет назад

Р=2(а+в) – для прямоугольника
Р=4а – для ромба или для кавадрата
где “а” и “в” – стороны четырехугольника, а Р – периметр

S=a*a – если все стороны равны
S=a*в – если стороны разные
где “а” и “в” – стороны четырехугольника, а S – площадь

Маhаббат Mammadova

Мудрец

(15818)

13 лет назад

esli eto chetiryoxuqolnik romb S=ah,S=a^2*sina,esli pareleloqram S=ab*sina,esli kvadrat S=a^2.esli pryamouqolnik S=a*b,esli trapechiya S=a+b/2*h

Анастасия Сироткина

Ученик

(247)

7 лет назад

щя голова зорвётся

Источник

Как найти площадь четырехугольника

При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.

1

Как найти площадь четырехугольника

Многоугольник произвольный

Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.

S = (d1*d2*sinα)/2,
d1, d2 – диагонали,
α – угол, полученный путем их пересечения.

Четуг

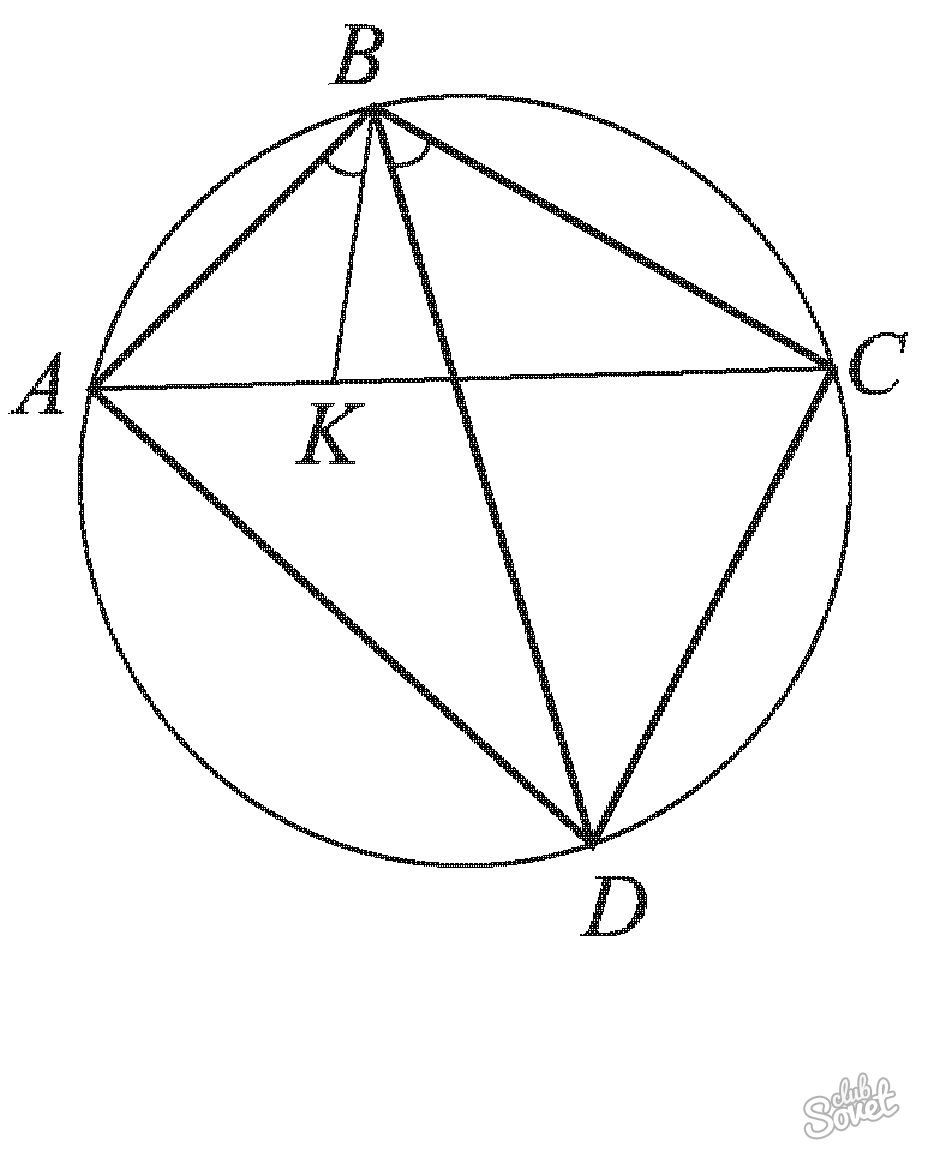
Многоугольник в окружности

Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:

S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
m, k, l, e – его стороны.

2

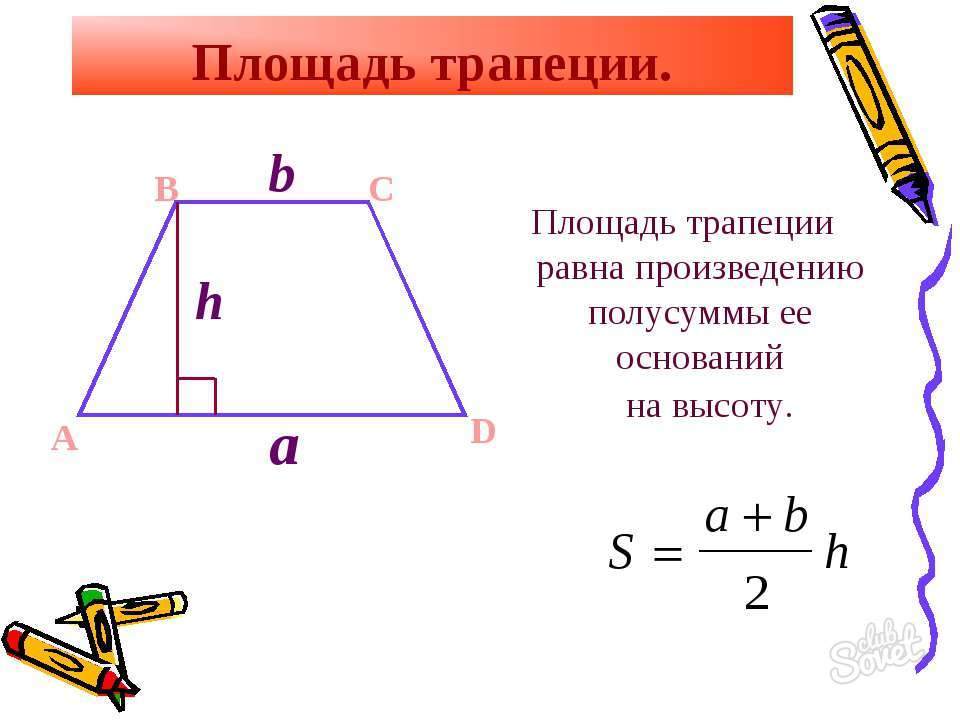
Как найти площадь четырехугольника – трапеции

Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:

Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
a и b – основания,
h – перпендикуляр-высота.
Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
k – линия средины.
Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
d1, d2 – диагонали,
β – угол, полученный путем их пересечения.
Заданы 4 стороны: S = ((m + l)√k² – ((m – l)² + k²– d²)²/(4(m – l)²))/2,
m, l – стороны параллельные,
k, d – стороны боковые.

3

Как найти площадь четырехугольника – дельтоида

Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:

Известны стороны фигуры и угол, образованный сторонами разной длины:
S = m*l*sinϕ,
m, l – стороны дельтоида,
ϕ – угол между ними.
Известны стороны фигуры и углы, образованные сторонами равной длины:
S = m²*sinα/2 + l²*sinβ/2,
m, l – стороны дельтоида,
α, β – углы между равными сторонами.
Наличие известных диагоналей также позволяет определить площадь фигуры:
S = d1*d2/2,
d1, d2 – диагонали дельтоида.
Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
m, l – стороны дельтоида,
r – радиус в случае вписанной окружности.

4

Как найти площадь четырехугольника – параллелограмма

Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.

Общее выражение

Для определения площади данного вида фигуры потребуются:

Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
k – сторона фигуры,
h(k) – высота к ней.
Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
S = l*k*sinϕ,
k, l – стороны многоугольника,
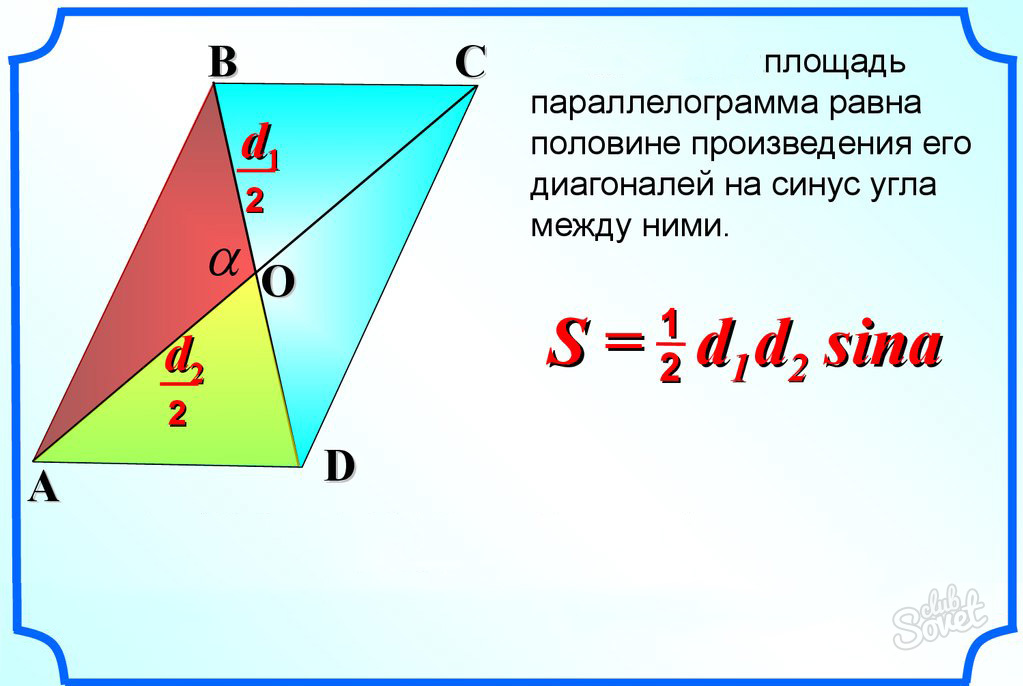
ϕ – угол между ними.
Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
d1, d2 – диагонали,
β – угол – результат их пересечения.

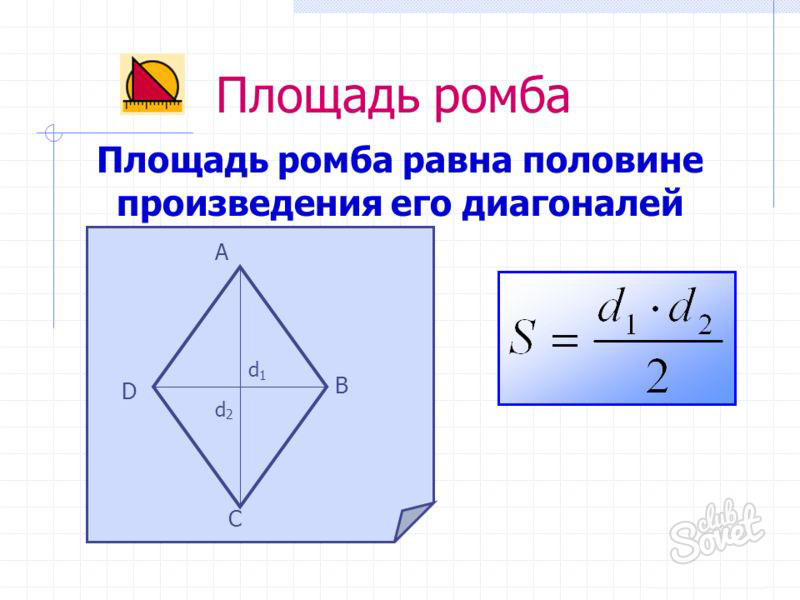
Ромб

Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда

S = k*h(k),
k – сторона фигуры, h(k) – высота к ней.
S = k²*sinϕ,
k – сторона четырехугольника, ϕ – угол между сторонами.
S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
d1, d2 – диагонали многоугольника.

Прямоугольник

Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:

S = k*l,
k, l – стороны фигуры.
S = d²*sinβ/2,
d – диагонали четырехугольника, β – угол – результат их пересечения.
S = 2R²*sinβ,
R – радиус в случае описанной окружности.

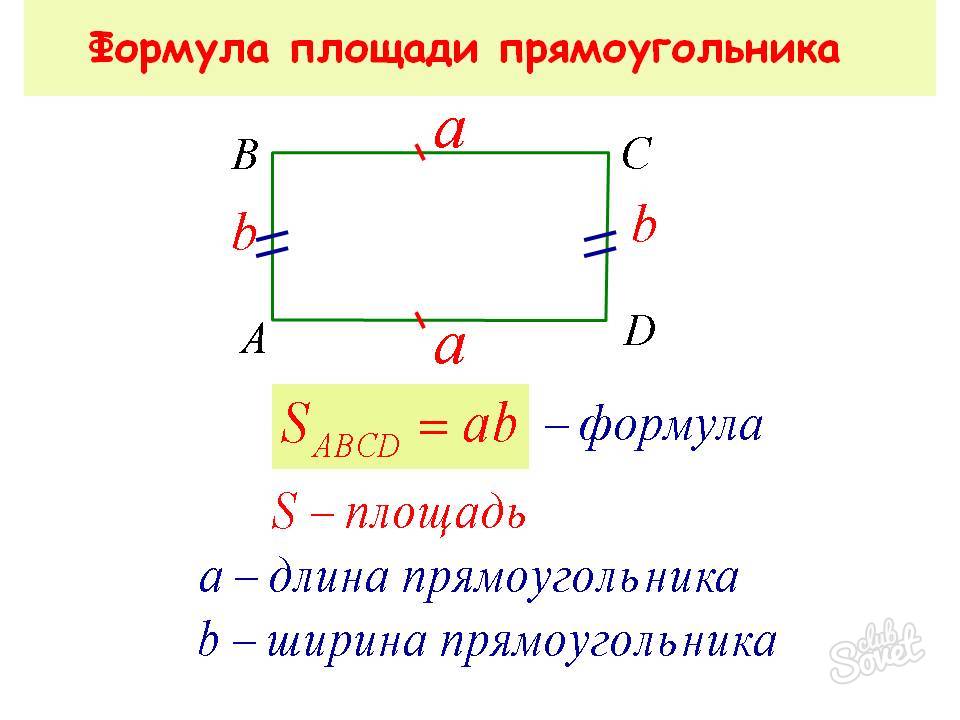
Квадрат

В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т.к. стороны такого вида прямоугольника равны):

S = k², k – сторона фигуры.

S = d²/2, d – диагональ квадрата.

S = 2R², R – радиус в случае описанной окружности.
S = 4r⁴, r – радиус в случае вписанной окружности.

Источник

Калькулятор расчета площади четырехугольника

Расчет площади

1. Через диагонали и угол между ними

2. По всем сторонам (формула Брахмагупты)

Формулы вычисления площади произвольного четырёхугольника

Определения и соглашения

Нахождение площади четырёхугольника различными способами и методами

Заключение

Видео

Площадь неправильного четырехугольника

Как найти площадь неправильного четырехугольника?

Советы

Об этой статье

Была ли эта статья полезной?

Условие

Рассуждение

Решение

Заключение

Применение