Как найти площадь четырехугольника если даны координаты

Формулы площади

Основные свойства и виды

К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:

Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:

Что такое четырех угольник

Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Площадь четырехугольника равна полупроизведению его диагоналей и угла между ними.

Четырехугольник – это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Четырехугольник – это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.

Формулы площади квадрата

где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.

Определения и соглашения

В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

1. Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
2. Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
3. Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
4. Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
5. Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
6. Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
7. Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
8. Угол между сторонами a и b будем обозначать следующей записью (a,b).

Площадь четырехугольника, заданного координатами

Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY .

Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле:
Найдем одну из сторон, к примеру, AB :
Подставим значения в формулу:
Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:

Формула вычисления площади

Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними:

S = 1/2 * d₁ * d₂ * sin α

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Особые виды четырехугольников

Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:

• Параллелограмм
• Ромб
• Прямоугольник
• Квадрат
• Трапеция
• Дельтоид
• Контрпараллелограмм

Квадрат, прямоугольник и другие параллелограммы

• Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
• Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
• Ромб — это параллелограмм, у которого все стороны равны.

• ‘Площадь = длина х высота, или S = a х h.
• Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров.
• Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).

• Площадь = сторона х сторона, или S = a 2.
• Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a 2 = 4 х 4 = 16 квадратных сантиметров.

• Площадь = (диагональ1 х диагональ2)/2, или S = (d₁ × d₂)/2
• Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.

• Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров.

• Площадь = сторона х высоту, или S = a × h
• Площадь = (диагональ1 × диагональ2)/2, или S = (d₁ × d₂)/2
• Пример: если сторона квадрата равна 4 см, то его площадь равна 4 х 4 = 16 квадратных сантиметров.
• Пример: диагонали квадрата равны по 10 см. Вы можете найти площадь этого квадрата по формуле: (10 х 10)/2 = 100/2 = 50 квадратных сантиметров.

Пример задачи

Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.

Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .

Свойство диагоналей выпуклого четырехугольника

Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:

На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.

Свойства длин сторон четырехугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.

Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.

В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.

Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство ( a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

Четырехугольник и окружность

Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).

Главное свойство описанного четырехугольника:

Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.

Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)

Главное свойство вписанного четырехугольника:

Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

где d₁ и d₂ – диагонали четырёхугольника , а φ – любой из четырёх углов между ними (рис. 1).

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

,

где r – радиус вписанной в ромб окружности , а φ – любой из четырёх углов ромба (рис.4).

Доказательство . Поскольку каждая из диагоналей ромба является биссектрисой угла , а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности . Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

,

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам) , то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора , составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

,

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида , дельтоида , можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Вычисление площади выпуклого многоугольника по координатам вершин на плоскости

Вычисление площади выпуклого многоугольника по координатам вершин. Выпуклый многоугольник строится по точкам с использованием алгоритма Джарвиса

Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.

Принцип работы остается таким же – многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон – Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку. Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже

При добавлении следующей точки, например, так, как на следующем рисунке

должен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.

Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.

Алгоритм работает за время , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.

Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника. Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.

Решение. Задание 3, Вариант 2

Найти площадь четырехугольника ABCD, если его вершины имеют координаты A(1;1),B(-3;2),C(3;1)и D(2;-2).

Проще всего найти площадь ABCD как сумму площадей треугольников ABC и ACD. Основание этих треугольников AC=2, а высоты соответственно 1 и 3. Площадь ABCD равна 1+3=4.

Проверьте, что вы соединили вершины четырехугольника по порядку: ABCD.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

• 
• 
• 
• 

Наш онлайн-курс по Физике

Все темы ЕГЭ с нуля

Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!

Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео

Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.

Мы обязательно ответим!

Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.

Результат будет выше, если готовиться по отработанной методике.

У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.

[spoiler title=”источники:”]

http://planetcalc.ru/7652/

http://ege-study.ru/ru/ege/podgotovka/matematika/probnyj-ege/2018-2/fevral/zadanie-3-reshenie/variant-2/

[/spoiler]

Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.

Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти площадь квадрата можно найти по сторонам, площадь ромба легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:

Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.

Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:

На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.

Площадь четырехугольника по сторонам

Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:

Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см. Для начала найдем полупериметр:

используем найденное значение для расчета площади:

Площадь четырехугольника, заданного координатами

Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.

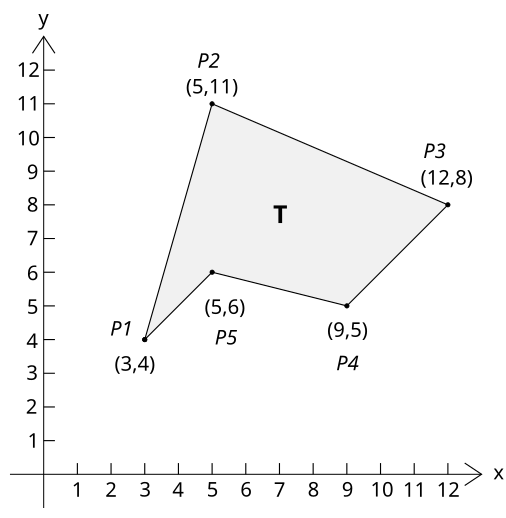
Площадь по заданным координатам. Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам? Какие есть формулы и методы, позволяющие находить площадь через координаты? бонус за лучший ответ (выдан): 5 кредитов Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая “формулой землемера”, “формулой геодезиста”, “формулой шнурования”, “алгоритмом шнурования”, а так же “методом треугольников”. Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи. Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки. Фигура многоугольника может иметь произвольную геометрию. Например: Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn). Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна: Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается. Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG. Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются: S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG) Площади трапеций рассчитываются по формуле; Sтрапеции = 1/2 *((a+b))*h, где a, b – основания трапеции, h – высота трапеции. Значения a, b и h вычисляются по координатам. В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле: автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Площадь фигуры по координатам вершин Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам. Эта формула выглядит следующим образом: Здесь: AB – отрезок, точка A имеет координаты (x1, y1), точка B имеет координаты (x2, y2). Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона: Здесь: S – площадь треугольника, a, b, c – стороны, p – полупериметр, который равен половине суммы сторон a, b и c. Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам: AB = √(4² + 4²) = √32 ≈ 5,66. AC = √(3² + (-3)²) = √18 ≈ 4,24. BC = √((-1)² + (-7)²) = √50 ≈ 7,07. Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49. Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04. 2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали: Здесь: S – площадь ромба, d1 и d2 – диагонали. Таким образом, нам нужно найти диагонали AC и BD. AC = √(4² + 0) = √16 = 4. BD = √(0 + (-4)²) = √16 = 4. Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8. 3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая: Здесь: S – площадь трапеции, a и b – основания, h – высота. Высота трапеции (пусть это будет BE) – это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD). Определим координаты её отрезка: координаты первой точки совпадают с точкой B, это (3,4). координаты 2 точки (точка E) будут (3,1) – так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D. Высота трапеции BE = √(0 + (-3)²) = √9 = 3. Теперь посчитаем длину оснований: BC = √(2² + 0) = √4 = 2. AD = √(5² + 0) = √25 = 5. Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5. Степа­н-16 [34.5K] 5 лет назад  Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам. Самый простой случай – для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат. Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем – площадь по формуле: половина произведения основания на высоту. И т.д. Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны. Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей. Элени­я [445K] 3 года назад  Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь. Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры – это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь. Пример 1. Ищем площадь треугольника. Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC. Даны значения: AC основание в промежутке от “-4” до “+4”, то есть длина основания равна восьми. Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой “0” на графике. Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 – 0 = 4 и y = 2 – 0 = 2 (BO). Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле: Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC. И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств: Пример 2. Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл. Бекки Шарп [71.2K] 3 года назад  Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса. У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту. S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ – 10. А теперь по теореме Гаусса. Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число. S= 0,5 х [3х6+6х6+9х2+5х2 – 2х6-6х9-6х5-2х3] = 10 Таким образом можно найти площадь любой сложной фигуры, зная ее координаты. dydyS­acha [10.8K] 5 лет назад  Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу. Алиса в Стран­е [363K] 3 года назад  Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит: Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n – количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать. Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник: Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6). Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится: Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной. dusel­ldorf [4.3K] 5 лет назад  Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании: где А – площадь многоугольника с заданными координатам его вершин, n – количество сторон многоугольника, (xi, yi) – координаты вершин многоугольника, i = 1, 2,…, n — номер вершины многоугольника. Барха­тные лапки [382K] 3 года назад  Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так: S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 – 3х9 – 4х10 – 7х7 – 6х6] = 8 (квадратных единиц) Как видим если применять при решении формулу Гаусса то решить такую задачку несложно. Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса – квадрат, треугольник и т.п. Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей. Знаете ответ?

Условие задачи

Найти площадь четырехугольника ABCD, если его вершины имеют координаты A(1;1), B(-3;2), C(3;1)и D(2;-2).

Решение

Проще всего найти площадь ABCD как сумму площадей треугольников ABC и ACD. Основание этих треугольников AC=2, а высоты соответственно 1 и 3. Площадь ABCD равна 1+3=4.

Проверьте, что вы соединили вершины четырехугольника по порядку: ABCD.

Ответ:

4.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 января 2022 года; проверки требуют 2 правки.

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии, лесном хозяйстве и других областях.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самопересекающегося многоугольника, который может быть выпуклым или вогнутым.

Определение[править | править код]

Формула может быть представлена следующим выражением:

где

S — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1][2]:

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Примеры[править | править код]

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

S для четырехугольника — переменные до x₄ и y₄:

Более сложный пример[править | править код]

Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

Объяснение названия[править | править код]

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.
Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.
В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Хорошее описание “Шнуровки Гаусса” представлено в видео на канале Wild Mathing [1]

См. также[править | править код]

• Планиметр
• Теорема Грина

Примечания[править | править код]