Нахождение площади прямоугольного параллелепипеда: формула и пример
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см 2 .
Полная площадь поверхности прямоугольного параллелепипеда
При изучении школьной математики часто встречаются задания, в которых требуется определить полную или боковую площадь поверхности прямоугольного или обычного параллелепипеда. Научимся это делать.
Для того, чтобы научиться вычислять площадь поверхности параллелепипеда необходимо представлять, что это такое.
Общие понятия
Изучим основные понятия. В дальнейших наших рассуждениях площадь будем обозначать латинской буквой S, угол между сторонами a и b будем обозначать как (ab).
Параллелепипедом в математике именуется четырехугольная призма, у которой все грани являются параллелограммами.
- Грань — одна из поверхностей пространственного тела.
- Параллелограмм — четырёхугольник с попарно параллельными противоположными сторонами.
- Поверхности параллелепипеда это сумма поверхностей всех его граней.
- Прямоугольный параллелепипед — пространственное тело у которого гранями являются прямоугольники.
- Прямоугольник — четырёхугольник у которого все углы прямые.
- Куб — пространственное тело у которого гранями являются квадраты.
- Квадрат — прямоугольник у которого все стороны равны между собой.
- Равными называются фигуры, совмещающиеся при наложении.

Нахождение площадей фигур
Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.
- Площадь квадрата равна произведению его стороны самой на себя. Формула площади квадрата имеет вид S = a*a = a^2.
- Прямоугольника – вычисляется с помощью умножения большей его стороны (длины) на меньшую его сторону (ширину). Формула площади прямоугольника имеет вид S = a*b.
- Параллелограмма – найти сложнее и имеется несколько различных способов. Наиболее часто в математике применяются формулы для нахождения с помощью стороны и опущенной на неё высоты или двух сторон и синуса угла между ними. Записываются они следующим образом: S = a*h, S = a*b*sin (ab).
Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур.
1. Длина стороны квадрата равна 1600 метров. Определим его площадь.
- S = a*a, отсюда в искомом случае S = 1600*1600 = 2 560 000 метров квадратных.
2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.
- S = a*b, следовательно в нашем варианте получится S = 90*200 = 18 000 метров квадратных.
3. С параллелограммом рассмотрим два случая нахождения.
Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:
- S = a*h = 300*250 = 75 000 метров квадратных.
Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:
- S = a*b*sin (ab) = 550*200*sin 30 = 110 000*0.5 = 55 000 квадратных метров.
Как видно из примеров, приведённых выше, никаких сложностей нет.

Площадь поверхности параллелепипеда
Так как наши тела имеют три принципиально различных варианта, то каждый из них мы рассмотрим в отдельности. Учтём, что полной поверхностью является сумма площадей всех граней тела, а боковой — только боковых граней.
Площадь поверхности куба
Здесь все крайне просто — грани этой фигуры равны между собой, так что S = a*a*6.
На примере это выглядит следующим образом:
Сторона равна 88 сантиметров. Площадь полной поверхности?
При данных условиях имеем:
S = a*a*6 = 88*88*6 = 46 464 сантиметра квадратного.
Площадь поверхности прямоугольного параллелепипеда
Здесь все так же довольно легко — нужно помнить, что противоположные грани равны. Таким образом, находим поверхность трёх различных граней, и каждую удваиваем. Формулы нахождения будут выглядеть следующим образом:
S = 2*(S1 + S2 + S3), где S1, S2, S3 площади всех граней соответственно.
Второй вариант S = 2*(a*b + a*c + b*c), где a, b, c соответствующие рёбра прямоугольного параллелепипеда.
Снова рассмотрим пример. Пусть рёбра прямоугольного параллелепипеда равняются 20, 30 и 40 метров. Площадь полной поверхности?
Имеем, S = 2*(a*b + a*c + b*c) = 2*(20*30 + 20*40 + 30*40) = 2*(600 + 800 + 1200) = 2*2600 = 5 200 квадратных метров.
Как видно, находить площадь прямоугольного параллелепипеда также совершенно несложно.
Поверхность параллелепипеда
Теперь рассмотрим случай когда заданное нам тело имеет вид простого параллелепипеда, его гранями являются обычные параллелограммы. Здесь, как и в предыдущем случае противоположные грани равны. Следовательно, определив поверхность трёх различных граней, мы сможем определить и полную поверхность. Значит, одна из формул опять-таки будет иметь вид:
- S = 2*(S1 + S2 + S3), где S1, S2, S3 площади трёх различных граней соответственно. Запишем исходя из наших рассуждений, ещё две формулы:
- S = 2*(a*h1 + b*h2 + c*h3), где a, b, c соответствующие рёбра параллелепипеда, а h1, h2, h3 опущенные на них высоты.
- S = 2*(a*b*sin (ab) + a*c*sin (ac) + b*c*sin (bc)), где a, b, c соответствующие рёбра, а (ab), (ac), (bc) углы между ними.
Снова приведём пример:
- a = 15, b = 25, c = 25, h1 = 10, h2 = 20, h3 = 15. Пл. полной поверхности? Согласно формуле получим:
- S = 2*(a*h1 + b*h2 + c*h3) = 2*(15*10 + 25*20 + 25*15) = 2*(150 + 500 + 375) = 2*1025 = 2 050 миллиметров квадратных.
В некоторых заданиях требуется определение только площади боковой поверхности параллелепипеда. В таком случае чётко указывается, что является основанием и находится только суммарная пл. четырёх боковых граней. Все приведённые выше рассуждения остаются верными.

Заключение
Тщательно изучив все сказанное выше, можно отметить, что никакой особой сложности задача по определению площади параллелепипеда не вызывает. Нужно всего-навсего чётко представлять все данные в материале математические понятия, абсолютно точно выучить формулы, ну и, разумеется, уметь хорошо проводить арифметические действия.
Видео
Из видео вы узнаете, как находить площать прямоугольного параллелепипеда.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$ – высота(она же боковое ребро);
$P_<осн>$ – периметр основания;
$S_<осн>$ – площадь основания;
$S_<бок>$ – площадь боковой поверхности;
$S_<п.п>$ – площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
Дополнительные сведения, которые пригодятся для решения задач:
$а$ – длина стороны.
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/<2>$, где $h_a$ – высота, проведенная к стороне $а$.
- $S=/<2>$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√$, где $р$ – это полупериметр $p=/<2>$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S=/<4R>$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S=/<4>$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S=/<2>$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S=<(a+b)·h>/<2>$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/polnaya-ploshhad-poverhnosti-pryamougolnogo-parallelepipeda
http://examer.ru/ege_po_matematike/teoriya/pryamiugolnyi_parallelepiped
[/spoiler]
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)

Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Площадь поверхности прямоугольного параллелепипеда


4.6
Средняя оценка: 4.6
Всего получено оценок: 490.
4.6
Средняя оценка: 4.6
Всего получено оценок: 490.
В 5 классе в курсе математики изучается тема прямоугольного параллелепипеда. Сегодня мы поговорим о формулах для нахождения площади боковой поверхности и площади полной поверхности этой фигуры, которые наиболее часто вызывают затруднения у учеников.

Материал подготовлен совместно с учителем первой категории Камушковой Натальей Владимировной.
Опыт работы учителем математики – 27 лет.
Определения
Параллелепипед – это фигура в пространстве, которая состоит из шести четырехугольников.
Каждый четырехугольник – это грань параллелепипеда. Среди граней различают четыре боковые и два основания. Если в основании фигуры находится прямоугольник, то многогранник называется прямоугольным параллелепипедом.
Стороны граней – это ребра. У параллелепипеда всего 12 ребер.
Параллелепипед имеет 8 вершин, для их обозначения используют заглавные латинские буквы.
Если две грани не имеют общего ребра, то они называются противоположными. Так как каждая грань прямоугольного параллелепипеда – это прямоугольник, у которого противоположные стороны равны, то и противоположные грани прямоугольного параллелепипеда также равны.
Длина ребер определяет основные характеристики прямоугольного параллелепипеда: площадь, периметр, объем.
Примеры таких фигур мы часто встречаем в нашей жизни: кирпич, коробка, системный блок компьютера.
Математическая фигура – прямоугольный параллелепипед активно используется в искусстве, архитектуре и прочих областях.
Различают несколько видов параллелепипедов, с основанием в виде квадрата, параллелограмма или прямоугольника.
Формула для нахождения площади
Для того, чтобы найти площадь боковой поверхности прямоугольного параллелепипеда, необходимо вычислить по отдельности площадь каждой боковой грани, а затем просуммировать получившиеся значения.
$S = ab$;
$S = ac$; где a, b, c – стороны фигуры.
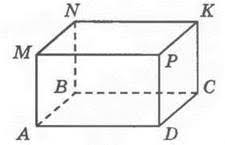
А так как противоположные грани равны, то есть $AMPD = BNKC$, $AMNB = DPKC$, их сумма и будет площадью боковой поверхности многоугольника.
$S= 2(ab + ac)$
Соответственно, чтобы вычислить площадь полной поверхности прямоугольного параллелепипеда необходимо сложить площадь боковой поверхности и две площади основания. В итоге получится формула площади прямоугольного параллелепипеда.
$S = 2(ab + ac) + 2 bc = 2(ab + ac + bc)$
Иногда для уточнения возле знака площади пишут краткое обозначение например, S п.п. – площадь полной поверхности, либо S б.п. – площадь боковой поверхности. Это помогает во время выполнения задания не перепутать нужные данные.
Пример задания
Найти площадь полной поверхности прямоугольного параллелепипеда, если длина и ширина основания 4 см и 3 см соответственно, а высота равна 2 см.
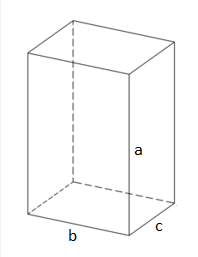
Решение:
S п.п. = 2(ab + ac + bc)
S п.п. = 2(4*3 + 4*2 + 3*2) = 52 см2
Таким образом, S п.п. = 52 см2.
Для площади поверхности прямоугольного параллелепипеда используют те же единицы измерения, в которых были приведены длины ребер. Если длины ребер прямоугольного параллелепипеда даны в разных единицах измерения, то их нужно перевести в одинаковые.

Что мы узнали?
Мы познакомились с элементами прямоугольного параллелепипеда: грани, ребра, основание. А также ознакомились с формулами для нахождения площади его боковой и полной поверхности, которые можно использовать для решения заданий.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Марина Яговцева
8/10
-

Розочка Ангелиночка
10/10
-

Слава Сироткин
10/10
-

Тома Зимина
7/10
-

Artem Sevastanov
10/10
-

Влад Чибиряев
10/10
-

Александр Селезнев
10/10
-

Акрам Сафарбеков
10/10
-

Вера Машковцева
10/10
-

Александр Семёнов
9/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 490.
А какая ваша оценка?

{S_{полн} = 2(ab+bc+ac)}
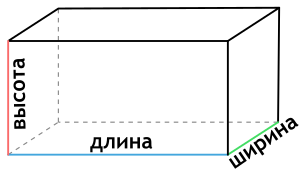
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер – это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота – это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}
a – длина прямоугольного параллелепипеда
b – ширина прямоугольного параллелепипеда
c – высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
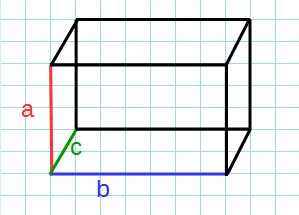
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
a, b, c – ребра параллелепипеда.
