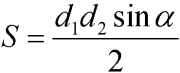Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
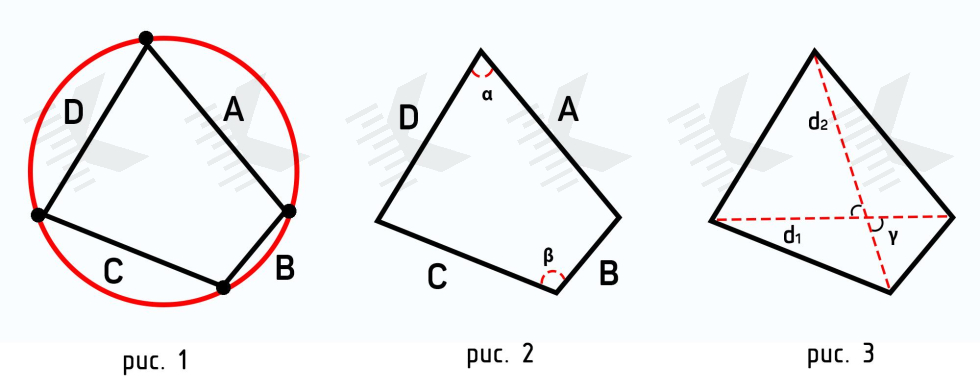
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
[spoiler title=”источники:”]
http://www.resolventa.ru/spr/planimetry/sqf.htm
[/spoiler]
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 – диагонали; α – угол между диагоналями.
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Площадь вписанного четырехугольника в окружность
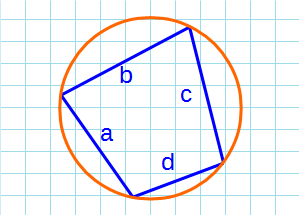
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
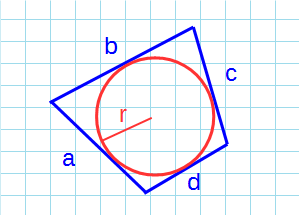
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
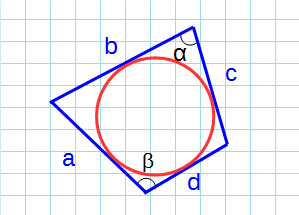
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Находить площадь фигуры можно не только по формулам, но чаще всего мы используем именно их. Первые формулы площади нам дают в 3 – 4 классах и это четырёхугольники – прямоугольник и квадрат. К сожалению, некоторые и эти формулы к экзамену не знают. Ну а мы рассмотрим задачу для решения которой будем использовать ещё более сложную формулу. Формулу площади произвольного (т.е. любого) четырёхугольника. Начнём?
Условие
Рассуждение
- В условии ни слова не сказано про диагонали;
- Точки M, F и K – середины сторон AB, AD и DC, а значит если их соединить, тополучатся отрезки соединяющие середины сторон (масло масляное);
- Отрезки FM и KF – известны, угол между ними ∠MFK – тоже, и это похоже на теорему косинусов, но MK – кажется бесполезным в решении отрезком.
Решение
Нарисуем произвольный четырёхугольник, то есть так, чтоб он не был похож ни на параллелограммы, ни на трапеции. И отметим середины сторон, известные отрезки и угол:
Отрезки MF и FK – соединяют середины сторон, что очень напоминает средние линии. Рассмотреть их помогут диагонали.
Теперь видно, что MF – средняя линия в ∆ABD, а FK – в ∆ACD.
Рассмотрим ∆ABD:
По свойству средне линии треугольника (равна половине параллельной ей стороны), можно найти диагональ BD, будет в 2 раза больше MF:
BD = 12√3 см.
Аналогично найдём диагональ AC через ∆ACD:
AC = 20 см.
Теперь нам известны обе диагонали найдём угол между ними. Для этого рассмотрим четырёхугольник NEHF:
Опять по свойству средней линий треугольника (только теперь параллельность стороне), определим тип четырёхугольника:
NEHF – параллелограмм ( противолежащие стороны параллельны).
Осталось найти площадь по формуле:
Подставим в формулу найденные диагонали и синус 120° (равен синусу 60°) и получим ответ.
Ответ: 180
Заключение
В этом решении мы применяли:
- Свойства средней линии треугольника.
- Формула площади произвольного четырёхугольника через диагонали и угол между ними.
Применение
Понять, что Вам нужна именно эта формула площади обычно проще, чем в рассмотренной задаче. Вам будут давать длины диагоналей или угол между ними, а найти нужно будет площадь. Могут наоборот дать площадь и попросить узнать диагональ или угол между ними. Формула встречается в первой части ОГЭ: ссылка на задания из открытого банка заданий ОГЭ.
Попробуйте решить и похожую на ту, что мы разобрали:
Пробуйте, решайте, изучайте, делитесь решениями в комментариях. Удачи!
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
-
Расчет площади
- 1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 3. Через полупериметр и радиус вписанной окружности
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
3. Через полупериметр и радиус вписанной окружности
Формула расчета
S = p ⋅ r
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
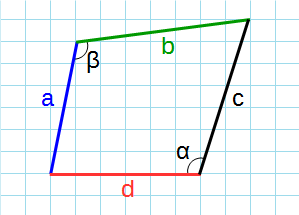
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
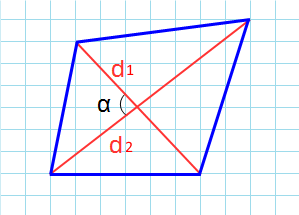
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
где d1, d2 — диагонали четырехугольника, α — острый угол между диагоналями.