Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
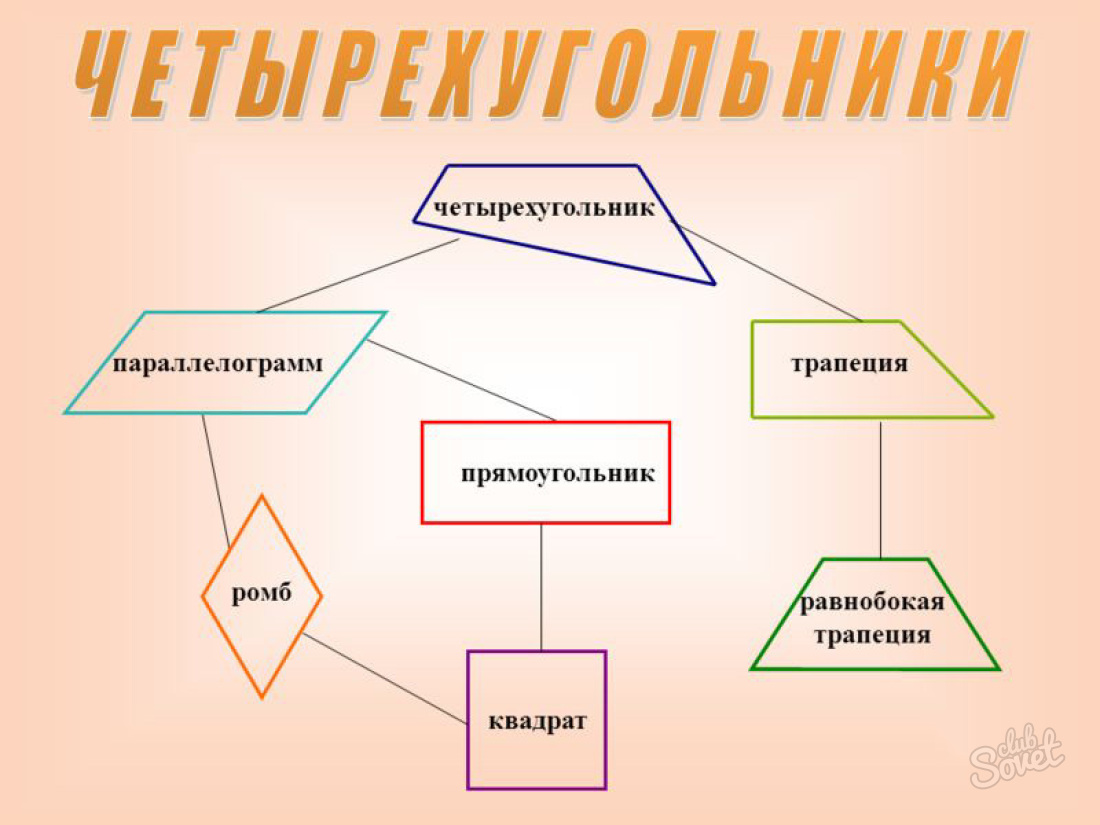
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
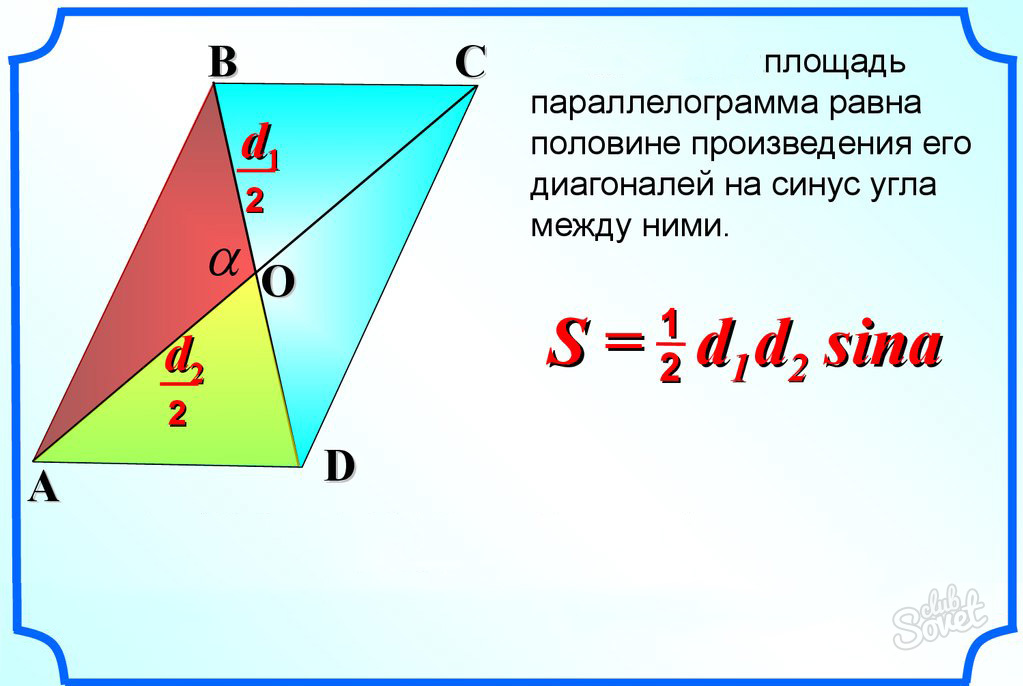
Через диагонали и угол между ними
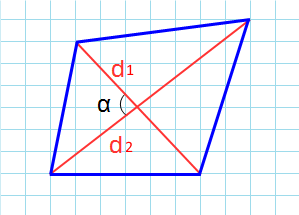
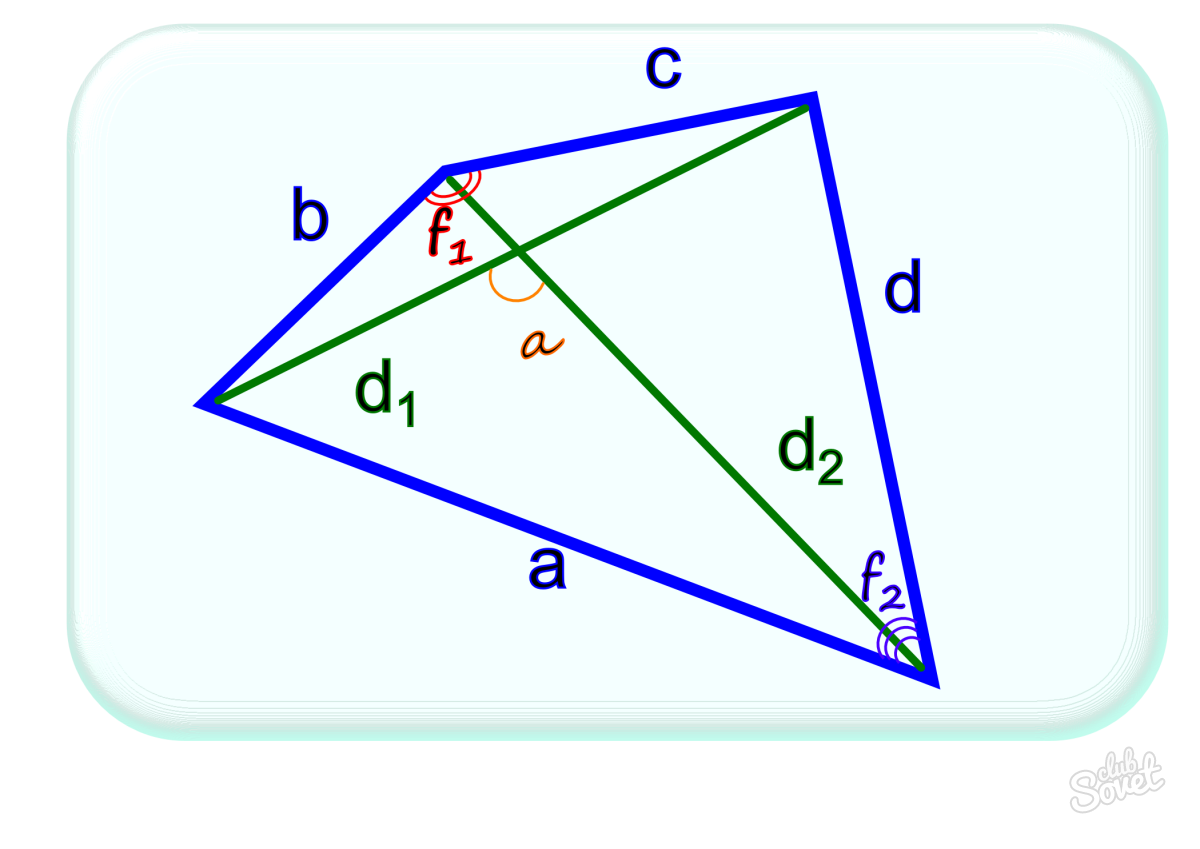
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 – диагонали; α – угол между диагоналями.
Через стороны и противолежащие углы
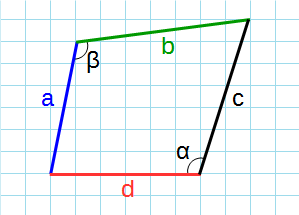
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
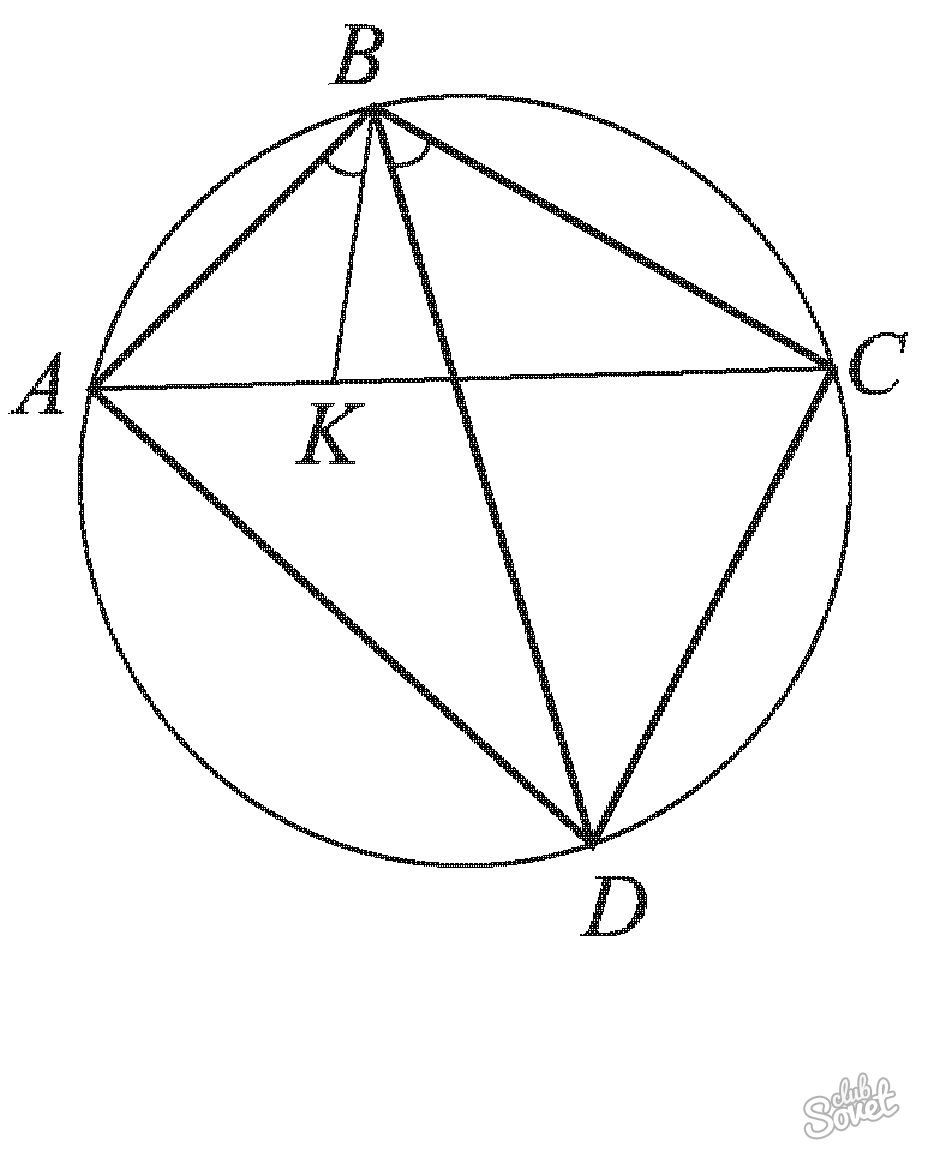
Площадь вписанного четырехугольника в окружность
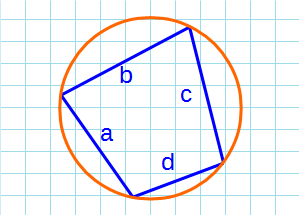
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
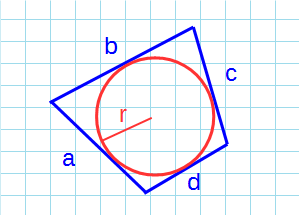
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p – полупериметр четырехугольника; r – радиус вписанной окружности; a, b, c, d – стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
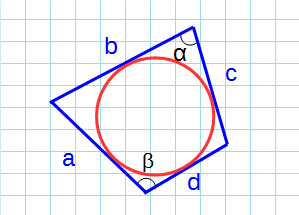
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p – полупериметр четырехугольника; a, b, c, d – стороны четырехугольника; α, β – противолежащие углы.
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | диагональ и угол между ними |  |
|
| 2 | стороны и углы между этими сторонами |  |
|
| 3 | стороны (по Формуле Брахмагупты) |
 |
|
| 4 | стороны и радиус вписанной окружности |  |
|
| 5 | стороны и углы между ними |  |
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
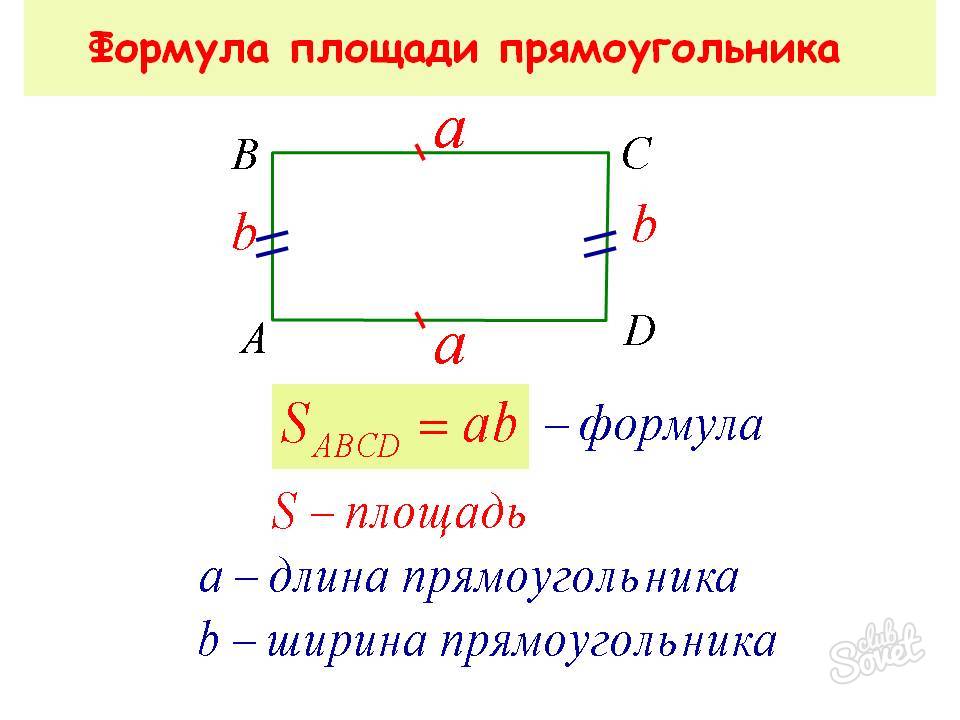
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
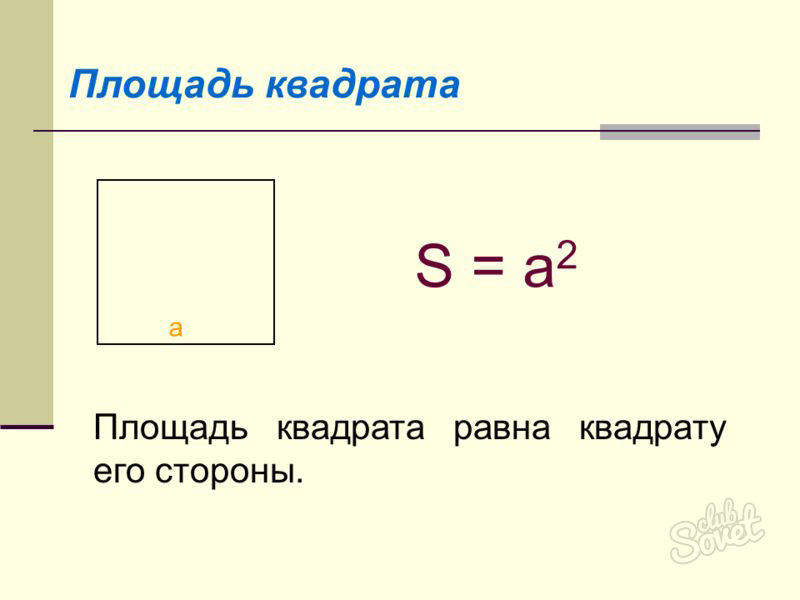
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
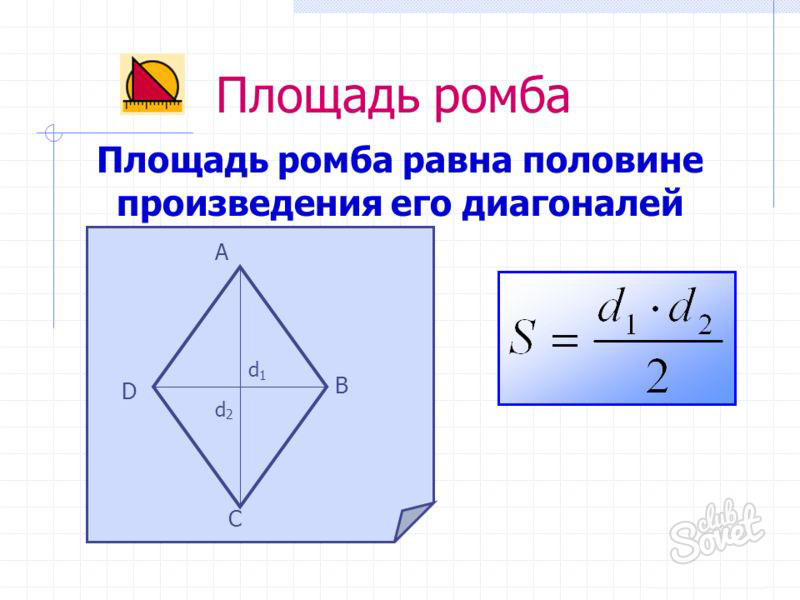
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
 |
|
 |
|
 |
|
| Параллелограмм | |
 |
|
 |
|
 |
|
| Квадрат | |
 |
S = a 2
где |
 |
S = 4r 2 |
 |
|
 |
|
| Ромб | |
 |
|
 |
|
 |
|
 |
|
 |
|
| Трапеция | |
 |
|
 |
|
 |
|
 |
|
| Дельтоид | |
 |
|
 |

где |
 |
|
 |
|
| Произвольный выпуклый четырёхугольник | |
 |
|
| Вписанный четырёхугольник | |
 |
| Прямоугольник |
 |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
[spoiler title=”источники:”]
http://doza.pro/art/math/geometry/area-tetragon
http://www.resolventa.ru/spr/planimetry/sqf.htm
[/spoiler]
Как найти площадь четырехугольника
При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.
1
Как найти площадь четырехугольника
Многоугольник произвольный
Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.
- S = (d1*d2*sinα)/2,
- d1, d2 – диагонали,
- α – угол, полученный путем их пересечения.
Многоугольник в окружности
Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:
S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
m, k, l, e – его стороны.
2
Как найти площадь четырехугольника – трапеции
Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:
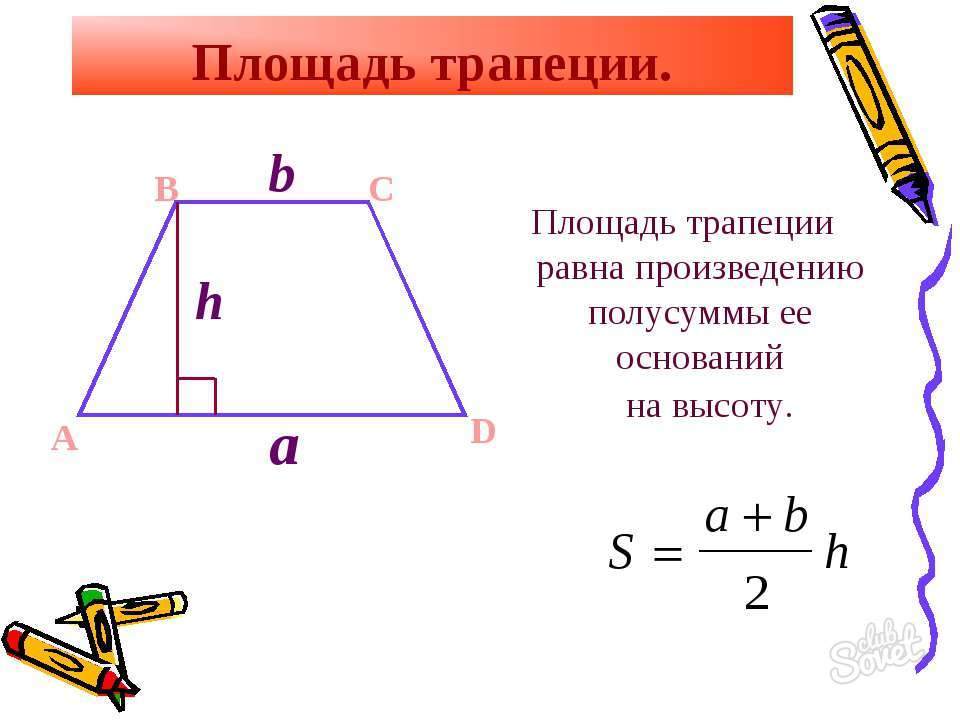
- Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
a и b – основания,
h – перпендикуляр-высота. - Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
k – линия средины.
Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
d1, d2 – диагонали,
β – угол, полученный путем их пересечения. - Заданы 4 стороны: S = ((m + l)√k2 – ((m – l)2 + k2– d2)2/(4(m – l)2))/2,
m, l – стороны параллельные,
k, d – стороны боковые.
3
Как найти площадь четырехугольника – дельтоида
Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:
- Известны стороны фигуры и угол, образованный сторонами разной длины:
S = m*l*sinϕ,
m, l – стороны дельтоида,
ϕ – угол между ними. - Известны стороны фигуры и углы, образованные сторонами равной длины:
S = m2*sinα/2 + l2*sinβ/2,
m, l – стороны дельтоида,
α, β – углы между равными сторонами. - Наличие известных диагоналей также позволяет определить площадь фигуры:
S = d1*d2/2,
d1, d2 – диагонали дельтоида. - Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
m, l – стороны дельтоида,
r – радиус в случае вписанной окружности.
4
Как найти площадь четырехугольника – параллелограмма
Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.
Общее выражение
Для определения площади данного вида фигуры потребуются:
- Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
k – сторона фигуры,
h(k) – высота к ней. - Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
S = l*k*sinϕ,
k, l – стороны многоугольника,
ϕ – угол между ними. - Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
d1, d2 – диагонали,
β – угол – результат их пересечения.
Ромб
Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда
- S = k*h(k),
k – сторона фигуры, h(k) – высота к ней. - S = k2*sinϕ,
k – сторона четырехугольника, ϕ – угол между сторонами. - S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
d1, d2 – диагонали многоугольника.
Прямоугольник
Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:
- S = k*l,
k, l – стороны фигуры. - S = d2*sinβ/2,
d – диагонали четырехугольника, β – угол – результат их пересечения. - S = 2R2*sinβ,
R – радиус в случае описанной окружности.
Квадрат
В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т.к. стороны такого вида прямоугольника равны):
- S = k2, k – сторона фигуры.
- S = d2/2, d – диагональ квадрата.
- S = 2R2, R – радиус в случае описанной окружности.
- S = 4r4, r – радиус в случае вписанной окружности.
Свойства вписанных и описанных четыехугольников
Содержание:
- Вписанный четырехугольник, особенности, основные свойства фигуры
- Описанный четырехугольник, особенности, основные свойства фигуры
- Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
- Чему равна сумма противоположных углов вписанного в окружность четырехугольника
- Как найти радиус вписанного в окружность четырехугольника, формула
Вписанный четырехугольник, особенности, основные свойства фигуры
Вписанный в окружность четырехугольник является таким четырехугольником, каждая из вершин которого принадлежит описанной около него окружности.
Вписанный в окружность четырехугольник изображен на рисунке:
Здесь около четырехугольника ABCD описана окружность, а сам этот четырехугольник можно назвать вписанным в данную окружность. Этот вывод можно сделать на основании определения, рассмотренного ранее, так как точки A, B, C, D являются одновременно и вершинами четырехугольника, и принадлежат описанной около него окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Какой-либо четырехугольник может быть вписан в некую окружность при условии, что его противолежащие углы в сумме дают 180°.
Теорема 2
В том случае, когда противолежащие углы некого четырехугольника в сумме составляют 180°, данный четырехугольник может быть вписан в окружность.
На примере рисунка запишем смысл изложенной теоремы:
(left. begin{array}{l} angle A + angle C = {180^o}\ angle B + angle D = {180^o} end{array} right} Leftrightarrow ABCD) треугольник вписан в окружность.
Следствие 1
Не каждый параллелограмм допустимо вписывать в окружность, лишь прямоугольники — в том числе квадраты.
Если какой-то четырехугольник вписан в окружность, то ее центральная точка совпадет с точкой, в которой пересекаются диагонали вписанного четырехугольника. При этом радиус описанной около четырехугольника окружности составит половину от длины его диагонали, то есть:
(R = frac{1}{2}BD)
Радиус, окружности, описанной около некого четырехугольника с прямыми углами, можно вычислить с помощью следующей формулы, содержащей стороны прямоугольника:
(R = frac{1}{2}sqrt {A{B^2} + A{D^2}}.)
Представим, что прямоугольник имеет стороны, которые равны a и b. Тогда справедливо следующее соотношение:
(R = frac{1}{2}sqrt {{a^2} + {b^2}})
Следствие 2
Допустимо вписать в окружность лишь такую трапецию, которая является равнобедренной.
Выведем формулу для вычисления радиуса окружности, которая описана около равнобедренной трапеции. Искомая величина равна радиусу окружности, описанной около одного из треугольников, имеющего те же вершины, что и рассматриваемая трапеция:
ABC, ABD, ACD или BCD.
Описанный четырехугольник, особенности, основные свойства фигуры
Описанным четырехугольником называют такую геометрическую фигуру с четырьмя углами, каждая из сторон которой является касательной к окружности. Данная окружность считается вписанной в рассматриваемый четырехугольник.
Теорема 3
В любой четырехугольник допустимо вписать какую-либо окружность при условии, что его противолежащие стороны в сумме равны.
Заметим, что в данном случае соблюдено условие:
AB+CD=BC+AD
На основе теоремы можно сформулировать обратное утверждение. В том случае, когда противоположные стороны четырехугольника в сумме равны, то есть AB+CD=BC+AD, в такой четырехугольник ABCD допустимо вписать какую-либо окружность.
Теорема 4
Центральная точка окружности, вписанной в четырехугольник, совпадает с точкой, в которой пересекаются биссектрисы данной геометрической фигуры.
Заметим, что на рисунке биссектрисами углов, которые имеет четырехугольник ABCD, являются следующие отрезки:
- AO;
- BO;
- CO;
- DO.
В результате:
(angle BAO = angle DAO)
(angle ABO = angle CBO) и так далее.
Теорема 5
Точки, в которых вписанная окружность касается описанного четырехугольника, расположены на сторонах с началом, совпадающим с одной вершиной, и находятся на одинаковом удалении от данной вершины.
Рассмотрим рисунок. Заметим, что:
BM=BK;
CK=CF;
DF=DN.
Записанные равенства вытекают из того факта, что это отрезки касательных, которые проведены из одной точки.
Запишем следующие соотношения:
(OM bot AB);
(OK bot BC);
(OF bot CD);
(ON bot AD).
Данные соотношения верны, так как включают в себя радиусы, которые проведены в точки касания окружности и описанного четырехугольника.
Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
В том случае, когда в четырехугольник вписана окружность, его площадь определяется по формуле:
(S = p cdot r)
Здесь p обозначает полупериметр четырехугольника.
Вспомним, что противолежащие стороны четырехугольника, в который вписана окружность, в сумме равны. Исходя из данного утверждения, можно сделать вывод: полупериметр такого четырехугольника равен какой-либо из пар сумм противолежащих сторон.
Если рассмотреть некий четырехугольник ABCD, то можно записать формулу для вычисления полупериметра этой геометрической фигуры:
p=AD+BC
p=AB+CD.
Тогда площадь четырехугольника, в который вписана окружность, будет вычислена таким образом:
({S_{ABCD}} = (AD + BC) cdot r;)
({S_{ABCD}} = (AB + CD) cdot r.)
В результате для определения радиуса окружности, которая вписана в некий четырехугольник, можно воспользоваться следующей формулой:
(r = frac{S}{p}.)
В том случае, если рассматривается описанная около четырехугольника ABCD окружность, то формула для вычисления ее радиуса примет вид:
(r = frac{{{S_{ABCD}}}}{{AD + BC}};)
(r = frac{{{S_{ABCD}}}}{{AB + CD}}.)
Чему равна сумма противоположных углов вписанного в окружность четырехугольника
Теорема 6
Если четырехугольник вписан в некую окружность, то его противолежащие углы в сумме дают .
Заметим, что на рисунке изображен четырехугольник ABCD, вписанный в окружность (O; R). Требуется доказать, что:
(angle A+angle C=180^o;)
(angle B+angle D=180^o.)
Представим доказательства. По условию:
(angle A) — угол вписанного четырехугольника, опирается на дугу BCD;
(angle C) — угол, который опирается на дугу DAB.
Зная, что вписанный угол составляет ½ часть дуги, которая является его опорой, запишем:
(angle A = frac{1}{2} cup BCD,)
(angle C = frac{1}{2} cup DAB.)
В результате:
(angle A + angle C = frac{1}{2} cup BCD + frac{1}{2} cup DAB = frac{1}{2}( cup BCD + cup DAB) = frac{1}{2} cdot 360^o = 180^o.)
Аналогичным образом запишем, что:
(angle B + angle D = frac{1}{2}( cup CDA + cup ABC) = frac{1}{2} cdot 360^o = 180^o.)
Теорема доказана.
Теорема 7
Если имеется такой четырехугольник, в котором противолежащие углы в сумме составляют (180^o), то около него можно описать окружность.
Представим, что имеется некий четырехугольник ABCD.
Сумма его противолежащих углов равна: (angle B+angle D=180^o).
Попробуем доказать, что около рассматриваемого четырехугольника можно описать окружность.
В первую очередь построим окружность около треугольника ABC таким образом, чтобы точка D принадлежала данной окружности. Построим доказательства, двигаясь «от обратного».
Допустим, что точка D не принадлежит окружности, которая описана около треугольника ABD. В таком случае точка D должна располагаться во внутренней области, ограниченной данной окружностью, или за пределами окружности.
В том случае, когда точка D расположена во внутреннем пространстве, ограниченном окружностью, какой-то луч AD имеет точку пересечения с окружностью. Обозначим ее, как Е. Заметим, что если вокруг четырехугольника ABCE описана окружность, то его противолежащие углы в сумме составляют (180^o):
(angle B+angle E = 180^o.)
Согласно данным из условия задачи:
(angle B+angle D=180^o.)
Таким образом:
(angle D=angle E.)
С другой стороны, угол D является внешним углом треугольника DCE при его вершине D. Исходя из этого, запишем:
(angle ADC=angle DEC+angle DCE.)
В результате получается, что угол D не равен углу E. Это утверждение противоречиво. Таким образом, точка D не расположена во внутреннем пространстве, ограниченном окружностью, описанной около треугольника ABC.
Луч AD имеет точку пересечения с окружностью, обозначенную буквой Е. В таком случае, ABCE представляет собой вписанный в окружность четырехугольник, а также:
(angle B+angle E=180^o)
Согласно условию задачи:
(angle B+angle D=180^o.)
Тогда:
(angle D=angle E.)
Однако угол Е является внешним углом треугольника ECD и расположен при вершине E.
Таким образом: (angle AEC=angle EDC+angle DCE.)
В результате недопустимо равенство углов D и E. В том случае, когда точка D расположена за пределами окружности, возникает противоречие. Таким образом, остается единственно верный вариант расположения этой точки, согласно которому она принадлежит окружности, описанной около четырехугольника. Теорема доказана.
Согласно свойству и признаку четырехугольника, вписанного в окружность, необходимым и достаточным условием вписанного четырехугольника является следующая теорема.
Теорема 7
Около четырехугольника допустимо описать окружность лишь в том случае, когда его противолежащие углы в сумме составляют 180 градусов.
Как найти радиус вписанного в окружность четырехугольника, формула
Допустим, что имеется некий четырехугольник, стороны которого обозначены, как a, b, c, d, а полупериметр равен p. В таком случае описанная около данного четырехугольника окружность имеет радиус, который можно рассчитать по формуле как отношение:
(R={frac {1}{4}}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}}.)
Примечание
Формулу радиуса окружности, которая описана около четырехугольника, ввел индийский математик Ватассери Парамешвара в XV веке.
Рассмотрим еще одну закономерность, которую называют формулой Брахмагупты. С ее помощью можно определить площадь S четырехугольника, который вписан в окружность и имеет стороны, равные a, b, c, d:
(S={sqrt {(p-a)(p-b)(p-c)(p-d)}}.)
В данном случае p является полупериметром, то есть в два раза меньше, чем периметр, и определяется как:
(p={tfrac {1}{2}}(a+b+c+d).)
С помощью формулы Брахмагупты представляется возможным изменить форму записи формулы Парамешвары:
(4SR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}.)
Здесь S определяется, как площадь четырехугольника, вписанного в окружность. Диаметр равен двум радиусам и проходит через центр окружности.
Вписанные и описанные четырехугольники
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
Рассмотрим теоремы о вписанных и описанных четырехугольниках и их свойствах.
Теорема 1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны
Теорема 2. Четырёхугольник можно описать вокруг окружности тогда и только тогда, когда суммы его противоположных сторон равны.
Теорема 3. Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.
Теорема 4. (Птолемея). Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Теорема 5. Площадь описанного четырехугольника равна произведению полупериметра четырёхугольника на радиус вписанной в него окружности.
Теорема 6. Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Теорема 7. Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Теорема 8. Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Теорема 9. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 10. В любой ромб можно вписать окружность.
Теорема 11. В любой квадрат можно вписать окружность.
Теорема 12. В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом.
Теорема 13. В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Теорема 14. В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований.
Посмотрим, как эти свойства применяются в решении задач ЕГЭ.
Задача 1. Два угла вписанного в окружность четырехугольника равны и
. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна . Пусть угол
равен
. Тогда напротив него лежит угол в
градусов. Если угол
равен
, то угол
равен
.
Ответ: 122.
Задача 2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен
.
Решение:
Пусть сторона равна
,
равна
, а
. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,
Получается, что равна
. Тогда периметр четырехугольника равен
. Мы получаем, что
, а большая сторона равна
.
Ответ: 12.
Задача 3. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.
Решение:
Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны и
, а боковые стороны —
и
. По свойству описанного четырехугольника,
, и значит, периметр равен
.
Получаем, что , а средняя линия равна
.
Ответ: 10.
Задача 4. Угол A четырехугольника , вписанного в окружность, равен
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Четырехугольник вписан в окружность. Значит, сумма его противоположных углов равна
Поэтому
Ответ: 148.
Задача 5. Углы четырехугольника
относятся как
. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Решение:
Пусть
Сумма всех углов четырехугольника равна
А сумма каждой пары противоположных углов равна (т.к. четырехугольник вписан в окружность).
Запишем эти два условия в виде двух уравнений с двумя неизвестными:
Подставляем второе уравнение в первое и получаем
Ответ: 90.
Задача 6. Стороны четырехугольника
и
стягивают дуги описанной окружности, градусные величины которых равны соответственно
и
. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна .
Поэтому
Угол А – вписанный, опирается на дугу , равную сумме дуг
и
, т.е.
Тогда вписанный угол А равен половине дуги , т.е.
Ответ: 107.
Задача 7. Точки расположенные на окружности, делят эту окружность на четыре дуги
и
градусные величины которых относятся соответственно как
Найдите угол A четырехугольника
Ответ дайте в градусах.
Решение:
Угол А – вписанный, опирается на дугу равную сумме дуг
и
Найдем дуги
и
Обозначим градусные величины дуг и
как
согласно заданному соотношению между дугами.
Тогда или
Сумма дуг и
составляет
Вписанный угол А равен половине дуги т.е.
Ответ: 15.
Задача 8. Радиус окружности, описанной около квадрата, равен Найдите длину стороны этого квадрата.
Решение:
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата. Тогда диагональ квадрата равна
Выразим сторону квадрата через его диагональ:
Ответ: 32.
Задача 9. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Решение:
Если правильный шестиугольник вписан в окружность, то радиус окружности равен стороне шестиугольника. Поэтому сторона равна 6.
Ответ: 6.
Задача 10. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Решение:
Поскольку трапеция вписана в окружность, она равнобедренная.
Рассмотрим равнобедренную трапецию с основаниями
Тогда боковые стороны
Проведем параллельно
Тогда треугольник
– равнобедренный, т.к.
и равносторонний, т.к.
Поэтому
– параллелограмм по построению, но
, поэтому
– ромб, и
Получаем, что О – центр описанной окружности с радиусом, равным меньшему основанию –
Ответ: 6.
Задача 11. Найти диагональ параллелограмма, вписанного в окружность радиусом 6 см.
Решение:
Согласно одной из теорем, окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру, см.
Ответ: 12.
Задача 12. Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Поэтому сумма оснований
Сумму боковых сторон найдем как разность между периметром и суммой оснований:
Трапеция вписана в окружность, следовательно, трапеция равнобедренная, боковые стороны равны:
Ответ: 5.
Задача 13. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и
Решение:
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру окружности.
В то же время по теореме Пифагора диагональ найдем как
Радиус окружности равен половине диаметра:
Ответ: 9.
Задача 14. Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение:
Радиус окружности, вписанной в квадрат, равен половине его стороны. Поэтому
Ответ: 8.
Задача 15. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна 11 (половине периметра).
Боковая сторона тогда боковая сторона
Радиус вписанной окружности равен половине т.е. 2.
Ответ: 2.
Задача 16. Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение:
Высота трапеции, в которую вписана окружность, равна диаметру этой окружности:
Ответ: 28.
Задача 17. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна
Средняя линия трапеции равна полусумме оснований
Ответ: 16.
Задача 18. Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 16. Найдите его площадь.
Решение:
Площадь описанного многоугольника можно найти как произведение полупериметра на радиус вписанной окружности:
Ответ: 16.
Задача 19. В равнобедренной трапеции, вписанной в окружность, диагонали взаимно перпендикулярны. Средняя линия трапеции равна 12. Найти радиус вписанной окружности.
Решение:
Радиус окружности, вписанной в трапецию, равен половине ее высоты.
Рассмотрим равнобедренную трапецию
Проведем Треугольник
– прямоугольный (с прямым углом С) и равнобедренный. Его гипотенуза
равна сумме оснований трапеции (т.к.
– параллелограмм, и
),
Высота трапеции является также высотой и медианой, проведенной из прямого угла равнобедренного прямоугольного треугольника
.
Радиус вписанной окружности
Ответ: 6.
Задача 20. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Решение:
Пусть О – центр описанной окружности. Проведем высоту проходящую через точку О. Тогда
(радиусы окружности),
Треугольники и
– прямоугольные. Применяя теорему Пифагора, найдем:
Ответ: 7.
Это были задачи по теме «Вписанные и описанные четырехугольники» из первой части ОГЭ и ЕГЭ. Покажем более сложную задачу, из второй части ОГЭ по математике.
Задача 21. В четырёхугольник можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника перпендикулярны. Найдите его площадь, если радиус описанной окружности равен 5, а
Решение:
Обозначим Тогда
Обозначим также
Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны.
Значит, Отсюда
Пусть О – точка пересечения диагоналей четырёхугольника
При пересечении и
образуется четыре прямоугольных треугольника. Это
Пусть
Запишем для каждого из этих треугольников теорему Пифагора:
Из
Из
Из
Из
Мы получили систему уравнений.
Сложив первое и третье из них и выразив как
получим:
Кроме того, Это мы нашли в самом начале.
Из системы уравнений
находим:
Значит,
Перестроим чертеж. Это надо сделать обязательно. Появились новые данные – рисуем новый чертеж. По условию, четырехугольник вписан в окружность.
Треугольники и
равны по трем сторонам. Значит, углы
и
равны.
Четырехугольник вписан в окружность, поэтому сумма углов
и
равна 180 градусов. Мы получили, что углы
и
– прямые. Тогда
– диаметр окружности.
По условию, , тогда
опирается на диаметр.
– прямоугольный,
– его гипотенуза.
По теореме Пифагора для :
Отсюда
Ответ: 40.
Если вы хотите разобрать большее количество примеров – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вписанные и описанные четырехугольники» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023