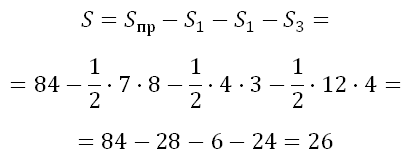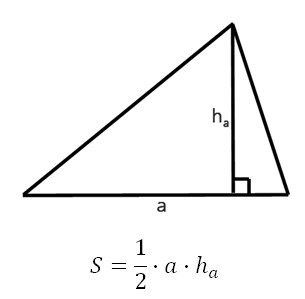Как найти площадь данного на рисунке треугольника - Сайт, где вы сможете решить свои вопросы

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Сторона треугольника равна 10, а проведённая к этой стороне высота равна 5. Найдите площадь треугольника.

В треугольнике одна из сторон равна 10, другая равна а угол между ними равен 60°. Найдите площадь треугольника.

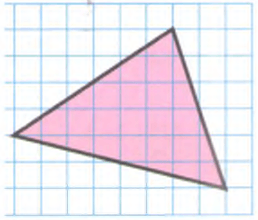
Найдите площадь треугольника, изображённого на рисунке.

В треугольнике ABC отрезок DE  — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.

На стороне AC треугольника ABC отмечена точка D так, что AD  =  3, DC  =  7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.

Источник: Банк заданий ФИПИ

Пройти тестирование по этим заданиям

Источник

Найдите площадь треугольника, изображённого на рисунке.

Оценив обстановку, я обратил внимание на то, что в задании ни слова не сказано ни о высоте треугольника, ни о том, является ли отрезок длиной 24 перпендикуляром. Стало быть, он может быть проведён под любым углом. Тут, как говорится, не верь глазам своим. Или о собственных глазах можно сказать иначе – доверяй, но проверяй. А как проверить?

Выдам вам один секретный способ. В интернете теперь много таких сайтов, которые решают задачи за нас. Они ещё называются «онлайн-калькуляторами». Заходишь на ресурс – открывается форма для ввода данных.

Стоит только ввести известные значения и нажать кнопку «рассчитать», через секунду получите ответ.

Опс! А ведь угол между катетами 24 и 32 действительно прямой. Только убедиться в этом можно было быстрее и проще. Как? Давайте попробуем для чисел 40, 32 и 24 подыскать общие делители. Во-первых, все числа чётные – делятся на 2 (20, 16 и 12). Кстати, и на 4 они тоже легко делятся без остатка (10, 8 и 6). Мало того, точно также и на 8 (5, 4 и 3). А это, обратите внимание, классический вариант Пифагоровой тройки. Соглашаемся – отрезок длиной 24 является перпендикуляром и одновременно высотой треугольника. В таком случае у нас два варианта решения задачи:

можно отдельно вычислить площадь левого прямоугольного треугольника, умножив основание на высоту и разделив на два (площадь равна половине произведения основания на высоту): 32 * 24 / 2 = 384
таким же образом узнать площадь второго: 10 * 24 / 2 = 120
просуммировать полученные значения: 384 + 120 = 504.

Другой способ:

сначала вычисляем длину основания треугольника: 32 + 10 = 42, а потом
по той же формуле находим площадь: S = (42 * 24) / 2 = 1008 / 2 = 504
S = 504

Кстати, проверить окончательный ответ можно с помощью всё того же онлайн-калькулятора:

Как видите, всё сходится. Простите за тавтологию, но за свой ответ отвечаю! Удачи на дорогах!

MTetyana
[172K]

3 дня назад

Из школьной программы, хорошо помню, что площадь треугольника можно найти по формуле: произведение основания и высоты, делённое на два

S=(a•h):2

И что интересно, все данные для решения есть на рисунке.

Поэтому ответ на этот вопрос будет таким:

а=32+10=42

S=(42•24):2=504

Тут не написано, в каких единицах даны измерения. Предположим что в сантиметрах. Тогда площадь этого треугольника будет равна 504 см2

Задачку легко решит любой школьник, кто проходил эту тему по математике.

Правда ещё можно найти площадь треугольника другим, не таким коротким способом, сложив площади друх прямоугольных треугольников, из которых этот треугольник состоит.

S1=(24•32):2=384

S2=(24•10):2=120

S= 384+120=504см2

Единственное, что меня удивляет – зачем на чертеже даны длины боковых сторон треугольника?

Наверное, прикол в том чтобы сбить с толку, чтобы мозги поломали над решением этой простейшей задачки)

Молодец автор этого вопроса!)

Vladimir 1215
[180K]

3 дня назад

Площадь данного треугольника можно определить по известным двум величинам-стороне и его высоте.

Причём, необходимо знать величину стороны этого треугольника и высоты, которая проведена к этой стороне. Формула площади треугольника а*h/2(a – сторона треугольника, h – его высота).

Исходя из этого, сначала определим величину основания треугольника:

32+10=42

Теперь величину основания надо умножить на величину высоты и результат разделить на 2. В результате вычислений получаем площадь треугольника:

(42*24)/2=1008/2=504.

Ответ – площадь треугольника составляет 504.

Kjdm Rfghfkjdf
[2.2K]

4 дня назад

Судя по рисунку, сторона, равная 24, является высотой, тогда: Треугольник 24-26-10-прямоугольный, и соответственно треугольник 40-24-32 тоже прямоугольный.

Можно достроить до прямоугольника и треугольник 24-26-10 и другой треугольник 40-24-32,найти площади этих прямоугольников, суммировать и разделить на два.

Можно воспользоваться формулой нахождения площади треугольника.:

Тогда S=1/2*(32+10)*24=504

Ответ:504

Натусииииии2023
[1.8K]

4 дня назад

Площадь треугольника равняется половине его основания умноженного на высоту. S=1/2A *h

Основание треугольника=32+10=42

S = 42/2*24=504 м2

Знаете ответ?

Источник

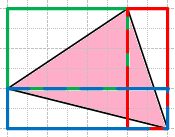
Найди площадь треугольника, изображенного на рисунке.

reshalka.com

ГДЗ учебник по математике 4 класс Дорофеев. Часть 2 страница 7. Номер №10

Решение

1) (6 * 4) : 2 = 24 : 12 = 12 (кв.ед) − площадь треугольника в зеленом прямоугольнике;
2) (8 * 2) : 2 = 16 : 2 = 8 (кв.ед) − площадь треугольника в синем прямоугольника;
3) (6 * 2) : 2 = 12 : 2 = 6 (кв.ед) − площадь треугольника в красном прямоугольнике;
4) 8 * 6 = 48 (кв.ед) − площадь всего прямоугольника;
5) 48 − (12 + 8 + 6) = 48 − 26 = 22 (кв.ед) − площадь закрашенного треугольника.
Ответ: 22 кв.ед.

Источник

Здравствуйте! В этой статье мы разберём задачи на нахождение площади треугольника построенного на листке в клетку (масштаб клетки 1×1). Фигуры на листе в клетку с вычислением их площади — это целая группа типов задач входящая в экзамен по математике. Кроме треугольника рассматриваются следующие фигуры — трапеция, параллелограмм, ромб, квадрат.

Решение заданий с треугольником труда не представляет, относятся они к простейшим. Для решения необходимо знать формулу площади треугольника и знать один приём, о котором я вам расскажу ниже.

Вообще, способов нахождения площади любой фигуры, построенной на листе в клетку существует более пяти. Все здесь рассматривать не будем, в интернете вы без труда найдёте их описание. Уверен, что тех рекомендаций, которые представлены будет вполне достаточно для решения.

Итак! Вам необходимо знать и понимать одну из основных формул площади треугольника, она наиболее часто используется при решении:

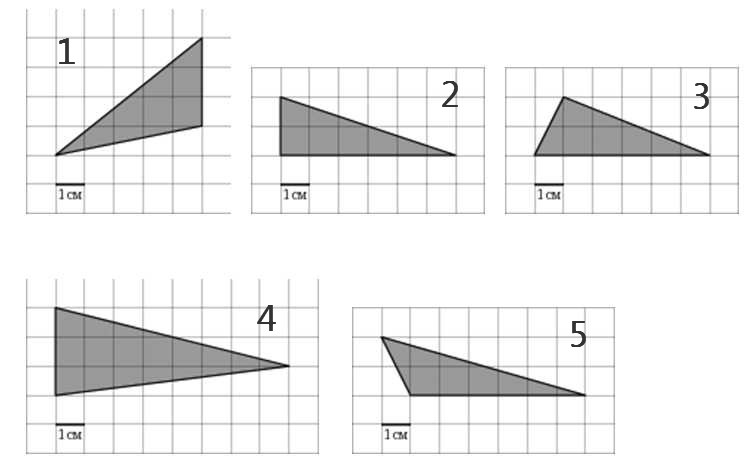
Длину основания и высоту считаем по клеткам. В задаче 27545 это наглядно показано. То есть, если перед вами задача, где треугольник построен именно таким образом, то считаем оговоренным способом. Например, рассмотрим треугольники:

У всех этих треугольников можно по клеткам установить длину основания и высоту. У первого основание равно 3, высота 5; у второго основание 6, высота 2; у третьего основание 6, высота 2; у четвертого основание равно 3, высота 8; у пятого основание равно 6, высота 2. Подставив их в формулу, остаётся только вычислить площадь (без ошибки).

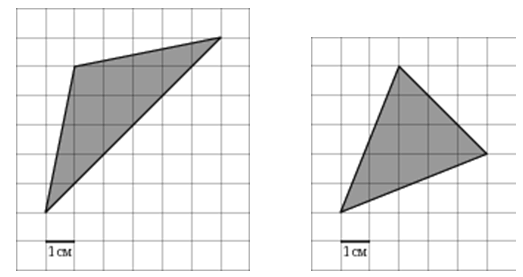
Есть задачи, в которых треугольники расположены так, что по клеткам длину основания и высоту посчитать неудобно (но можно), вот примеры:

В задачах, где будут даны подобные треугольники, используйте способ, который по моему мнению универсален, его достоинство объясню в одной из следующих статей: «заключите» такой треугольник в прямоугольник, вычислите площадь прямоугольника, затем из его площади вычтите площади треугольников. Пример:

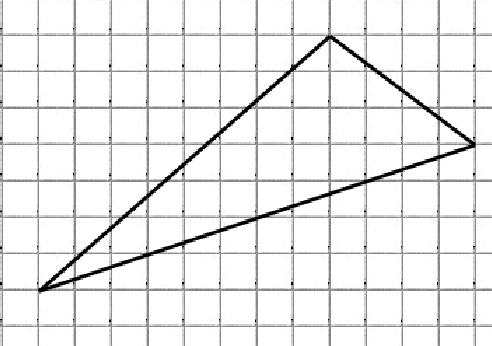
Найти площадь треугольника, изображённого на рисунке:

Заключим данный треугольник в прямоугольник:

Теперь вычислим площадь прямоугольника. Уверен, всем известно, что она равна произведению его соседних сторон:

Далее из его площади вычитаем площади трёх треугольников:

Ответ: 26

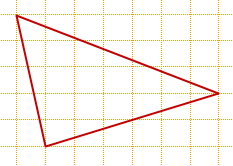
Есть ещё подобные задачи, но в них иначе представлено условие. Также нужно найти площадь треугольника, он построен на координатной плоскости, например:

Решения аналогичны: если можем установить длину основания и высоту треугольника по координатам, то далее площадь вычисляем просто по формуле:

В треугольнике на рисунке 1 этого сделать нельзя, поэтому советую построить данный треугольник по координатам на листе в клетку, и использовать уже рассмотренный нами метод, а именно описать около треугольника прямоугольник.

В будущем мы рассмотрим нахождения площадей параллелограммов, трапеций, четырёхугольников, элементов круга, а так же «сложных» фигур, не пропустите!

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

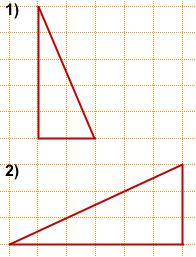
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

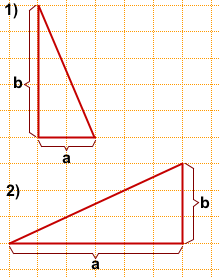
2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

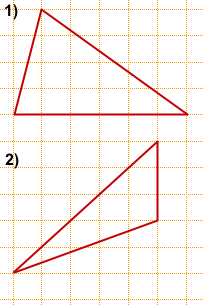
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

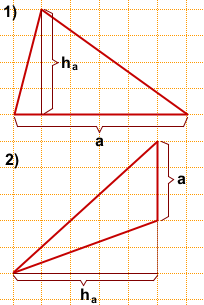
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

Задача 3

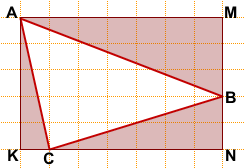
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

ГДЗ учебник по математике 4 класс Дорофеев. Часть 2 страница 7. Номер №10

Решение

Вам также может понравиться

Как найти егрн по адресу бесплатно

Как на светодиоде найти полярность

Как составить цели для подразделения

Добавить комментарий Отменить ответ