Площадь диагонального сечения параллелепипеда
У прямоугольного параллелепипеда диагональное сечение представляет собой прямоугольник.

Значит, для нахождения его площади нужно воспользоваться формулой площади прямоугольника:
S = a * b.
Сторона a совпадает с диагональю основания параллелепипеда.
Длину диагонали основания можно найти по теореме Пифагора, поскольку данная диагональ разбивает прямоугольник на 2 прямоугольных треугольника и является в каждом из них гипотенузой.
BD² = AB² + AD². => BD = √(AB² + AD²).
Сторона b равна высоте параллелепипеда (боковому ребру).
Высоту параллелепипеда можно, например, найти по его объёму и площади основания.
У прямоугольного параллелепипеда основание – это прямоугольник, поэтому площадь основания равна произведению его длины и ширины (на рисунке это AB и AD).
BB1 = V / (AB * AD).
Далее рассмотрим несколько примеров.
**
Пример 1
Стороны основания прямоугольного параллелепипеда равны 12 см и 4 см, а высота равна 5 см.
Нужно найти площадь диагонального сечения.
S (сеч) = √(12² + 4²) * 5 = √140 * 5 = 2√35 * 5 = 10√35 см.
**
Пример 2
Стороны основания и высота прямоугольного параллелепипеда относятся как 1:2:3, а его объём равен 48 см².
Нужно найти площадь диагонального сечения.
1) Сначала найдём, чему равны стороны основания и высота.
V = abc = 48.
Пусть a = x, b = 2x, c = 3x.
x * 2x * 3x = 48.
6x³ = 48.
x³ = 8.
x = 2.
Таким образом, стороны основания равны 2 и 4 см соответственно, а высота равна 6 см.
2) Теперь всё решается так же, как и в 1 примере.
S (сеч) = √(2² + 4²) * 6 = √20 * 6 = 2√5 * 6 = 12√5 см.
Как найти площадь диагонального сечения призмы
Призма — это многогранник с двумя параллельными основаниями и боковыми гранями в форме параллелограмма и в количестве, равном числу сторон многоугольника основания.

Инструкция
В произвольной призме боковые ребра расположены под углом к плоскости основания. Частным случаем является прямая призма. В ней боковые стороны лежат в плоскостях, перпендикулярных основаниям. В прямой призме боковые грани — прямоугольники, а боковые ребра равны высоте призмы.
Диагональное сечение призмы — часть плоскости, полностью заключенная во внутреннем пространстве многогранника. Диагональное сечение может быть ограничено двумя боковыми ребрами геометрического тела и диагоналями оснований. Очевидно, что число возможных диагональных сечений при этом определяется количеством диагоналей в многоугольнике основания.
Или границами диагонального сечения могут служить диагонали боковых граней и противоположные стороны оснований призмы. Диагональное сечение прямоугольной призмы имеет форму прямоугольника. В общем случае произвольной призмы форма диагонального сечения – параллелограмм.
В прямоугольной призме площадь диагонального сечения S определяется по формулам:
S=d*H
где d — диагональ основания,
H — высота призмы.
Или S=a*D
где а — сторона основания, принадлежащая одновременно плоскости сечения,
D — диагональ боковой грани.
В произвольной непрямой призме диагональное сечение — параллелограмм, одна сторона которого равна боковому ребру призмы, другая – диагонали основания. Или сторонами диагонального сечения могут быть диагонали боковых граней и стороны оснований между вершинами призмы, откуда проведены диагонали боковых поверхностей. Площадь параллелограмма S определяется формулой:
S=d*h
где d — диагональ основания призмы,
h — высота параллелограмма — диагонального сечения призмы.
Или S=a*h
где а — сторона основания призмы, являющаяся и границей диагонального сечения,
h — высота параллелограмма.
Для определения высоты диагонального сечения недостаточно знать линейные размеры призмы. Необходимы данные о наклоне призмы к плоскости основания. Дальнейшая задача сводится к последовательному решению нескольких треугольников в зависимости от исходных данных об углах между элементами призмы.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
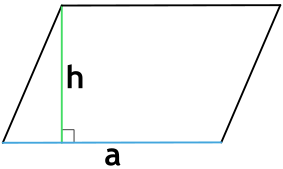
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
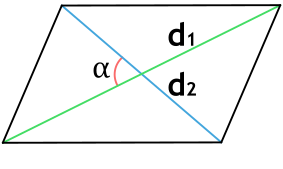
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
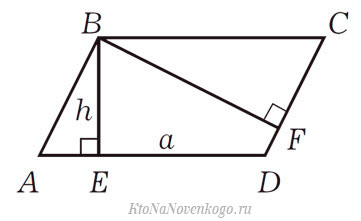
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
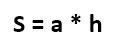
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
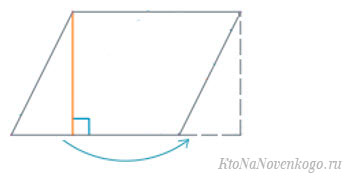
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
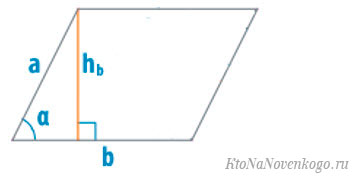
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
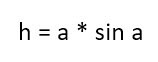
И наша конечная формула для расчета площади будет выглядеть следующим образом:
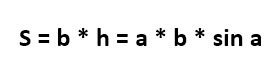
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
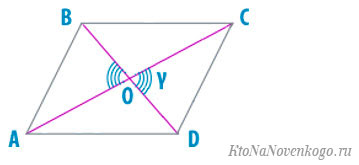
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
В этой статье будет раскрыта одна из математических тематик. Вы узнаете, как найти площадь параллелограмма. Данную тематику преподают в восьмом классе. Тем, кто не разобрался с ней, будет полезна эта статья.
Содержание
- Как найти площадь параллелограмма – свойства фигуры
- Расчет площади параллелограмма, если известны стороны, высота
- Расчет площади параллелограмма по диагоналям
- Расчет площади параллелограмма, если известны стороны, угол
- Видео: Площадь параллелограмма
В школе бывает так, что учитель объясняет урок, а дети не понимают. Потому дальше выходит, что ребенок не усваивает не только одну тему, а и те, что идут дальше. Особенно в геометрии. Ведь многие доказательства выводятся на основании правил и предыдущих теорем. Дальше узнаем, как найти площадь параллелограмма. Но изначально для того, чтобы узнать площадь, следует знать определение, что такое параллелограмм. Эта фигура представляет собой четырехугольник с параллельными сторонами и равными противоположными углами. Теперь давайте найдем площадь фигуры разными методами.
Как найти площадь параллелограмма – свойства фигуры
Итак, параллелограмм выглядит следующим образом:

Еще древнегреческий ученый математики Евклид описал несколько свойств данной фигуры в книге «Начала». А точнее две характеристики параллелограмма:
- фигуру можно сравнить и с прямоугольником, ведь все напротив лежащие стороны ее параллельны, равны, еще и пересекаются под углами 90°.
- также правило применимо и к квадрату, ромбу, отличие лишь в углах.
ВАЖНО: Прежде, чем приступить к доказательству, определимся с термином – площадь. Площадью называется размер самой фигуры, точнее плоскость занятая ею, что ограничивается самими сторонами данной фигуры.
Эти свойства недаром описаны выше, благодаря им будет легче узнать, как рассчитывать S – площадь фигуры.
Имеется несколько базовых формул, чтобы вычислить S – площадь параллелограмма:
- Когда даны: высота и длина параллелограмма
- Когда даны: длина одной и другой стороны фигуры, углы фигуры
- Когда даны: размеры обеих диагоналей, один из углов их пересечения.
Теперь о каждом из этих способов подробнее.
Расчет площади параллелограмма, если известны стороны, высота
Чтобы рассчитать величину S фигуры (площадь параллелограмма), следует знать все ее свойства. Выше уже были рассмотрены эти правила. Итак, первая формула – это нахождение площади фигуры по стороне и высоте. Пусть ВН – высота, а АВ – сторона. Высоту проводят на основание под углом 90º.

Выше предоставлено доказательство данной аксиомы. Из него видно, что S = a • h. Кстати, площадь измеряют в квадратных единицах.
S = АВ • ВН, для начала вывода теоремы следует рассмотреть треугольники, образовавшиеся в результате проведения высот к одному и тому же основанию. Они между собой будут равны. Ну и тогда площадь прямоугольника образовавшегося будет равна площади параллелограмма. А ранее было доказано, что в S прямоугольника = a • h. Именно поэтому и параллелограмм будет иметь такую же формулу для вычисления площади.
Расчет площади параллелограмма по диагоналям
Найти площадь параллелограмма можно различными методами. И этот вариант является распространенным. Для того, чтобы рассчитать S следует знать величину угла и длины диагоналей параллелограмма. Эта аксиома тоже важна в геометрии, зная ее вы с легкостью сможете решить задачи на контрольных и самостоятельных работах.

Для доказательства следует рассмотреть два равных треугольника, что получились при разделении параллелограмма на две части.

По трем сторонам. Значит и углы в этих треугольниках равны, смотрите рисунок выше. А площадь треугольника равняется половине произведения стороны a на высоту h. А высота в данных треугольниках – это и есть диагональ параллелограмма. Отсюда и выходит, что S параллелограмма равняется площади этих двух треугольников или 1/2 sin α на произведение диагоналей.
- S = 1/2 • sin α • d1 • d2
Что и требовалось найти.
Расчет площади параллелограмма, если известны стороны, угол
Если вы знаете чему равны длины обеих сторон, угол, то сможете найти и S параллелограмма. Площадь параллелограмма в этом случае равна:
- S = b • a • sin∠α.
Для того, чтобы доказать данную аксиому, достаточно по формулам найти высоту фигуры и подставить найденные данные в известную формулу параллелограмма.

По правилам геометрии, если рассматривать треугольники, то sin угла будет равен отношению противолежащего h – катета к гипотенузе. А вот катет, это и есть высота фигуры. Вот и выходит:
- sin β = h/a
Из этого равенства можно высчитать, чему равняется высота:
- h = sin β • a
Теперь остается подставить все элементы в формулу и выйдет следующее:
- S параллелограмма = h • b • sin β
