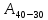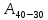Как найти площадь дсо

Вычисление площади для углов крена от 0 до 30°

Для вычисления пользуются формулой:

где,

S — Площадь под кривой плеч статической остойчивости.
h — Интервал между ординатами.
a, b, c, d — Ординаты плеч статической остойчивости соответственно для углов крена 0, 10°, 20° и 30°.

Пример: Вычислить площадь под кривой плеч статической остойчивости до угла крена 30°, если значения плеч статической остойчивости следующие:

1. Для удобства вычислений составляют таблицу, где в графе ордината подставляют значения плеч статической остойчивости для углов крена соответственно 0, 10°, 20°, 30°:

Затем находят интервал между ординатами

2. После этого рассчитывают площадь под кривой плеч статической остойчивости:

Вычисление площади для углов крена от 0 до 40°

Для вычисления площади пользуются формулой:

где,

S — Площадь под кривой плеч статической остойчивости.
h — Интервал между ординатами.
a, b, c, d, e — Ординаты плеч статической остойчивости соответственно для углов крена 0, 10°, 20°, 30° и 40°.

Пример: Вычислить площадь под кривой плеч статической остойчивости до угла крена 40°. Значения плеч статической остойчивости приведены в таблице.

1. Для вычисления суммы, заносят значения плеч в таблицу:

2. Вычисляют интервал между ординатами

3. Вычисляют площадь под кривой плеч статической остойчивости:

Для более точного вычисления площади можно взять плечи статической остойчивости с интервалом в 5°. Тогда для вычисления площади до 30° пользуются формулой:

где,

a, b, c, d, e, f, g — плечи статической остойчивости соответственно для углов крена 0, 5°, 10°, 15°, 20°, 25° и 30°.

Для вычисления площади до 40° пользуются формулой:

где,

a, b, c, d, e, f, g, j, k — плечи статической остойчивости соответственно для углов крена 0, 5°, 10°, 15°, 20°, 25°, 30°, 35°, 40°.

В обоих случаях интервал между ординатами будет .
Если необходимо найти динамическую остойчивость судна до определенного угла крена, то сначала вычисляют площадь под кривой плеч статической остойчивости от 0 до определенного угла крена, а затем полученное значение умножают на водоизмещение судна.
Динамическая остойчивость судна измеряется в тонна-метро-радианах.

Пример: В приведенном выше примере требуется вычислить динамическую остойчивость судна водоизмещением 7550 тонн до угла крена 40°.
Динамическая остойчивость = 0,241 х 7550 = 1819,55 тонна-метро-радиан.

Вычисление площади под кривой плеч статической остойчивости требуется также при оценке запаса динамической остойчивости при перевозке зерна насыпью и при оценке динамической остойчивости судна по критерию погоды. Соответствующие алгоритмы рассмотрены в разделах «Вычисление площади на ДСО при оценке остойчивости по критерию погоды» и «Вычисление площадей на ДСО в зерновой остойчивости».

Больше информации по вопросам остойчивости судна можно найти в книге «Остойчивость грузовых судов».

---

Автор капитан В.Н. Филимонов

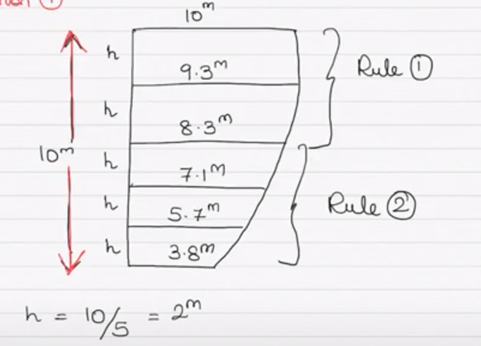
Правил Симпсона как и других расчета кривых площадей много, но из всех выделю три самые подходящие для расчетов остойчивости

Правила

Правило 1 – 141 – может быть расширено 14241 или 1424241 и так далее

Правило 2 – 1331 – может быть расширено 1332331 или 1332332331 и так далее

Правило 3 – 58

Также можно комбинировать правила, но об этом позже.

Каждое из них имеет формулы:

Правило 1 – Area = (1y1 +4y2 + 1y3)

Правило 2 – Area = (1y1 +3y2 + 3y3 + 1y4)

Правило 3 – Area = (5a +8b – c)

Правило 3 может иметь вид – Area = (-с + 5a +8b)

Где h – шаг. В случае с ДСО это шаг по оси X. При расчетах площадей под ДСО загвоздка заключается в том что нам нужны значения по оси y значений по оси X.

Так как значения по оси Y это плечи ДСО статической остойчивости рассчитанные ранее с шагом в 10 градусов то и при расчетах площадей шаг берем 10 градусов.

К примеру при расчете дсо мы обычно имеем деление диаграммы 0 10, 20, 30, 40, 50, 60 и тд, так вот шаг между ними 10.  Почему? Визуально мы видим что значения между собой равны. И достаточно одно вычесть из другого, 20-10 = 10.

Более правильно расчитать шаг можно следующим образом

Когда отсчет от 0 до определенного числа то как в нашем случае 60, а шагов от 0 6 то 60/6 = 10

Все сводится к тому что шаги должны быть одинаковые.

Не может быть 0 10 20 30 37, потому что шаги разные. В начале 10 а в конце 7.

Как быть?

Имеем мы крайнее значение 37 нужно высчитать шаги равные друг другу.

Для этого 0 не считаем, остается 4 шага.

37/4 = 9.25 – это и будет шаг диаграммы.

Получается

0 9,25 9,25 9,25 9,25

Доказательство – 9,25 9,25 9,25 9,25 = 37.

Так как шаги ДСО обычно рассчитывают шагом в 10 а иногда в 15, то значения по оси Y будут с таким шагом. А нам нужны значения для 9,25. Можно заново рассчитать, что долго, проинтерполировать( это не точно) и самый верный способ – снять эти значения с ДСО.

Назначение расчетов

Данные правила применяются для нахождения площади под кривой или любой площади, к примеру площади действующей ватерлинии (WPA). Но можно также найти и площадь по параболе и точкам соприкосновения с кривой (ддо).

Для расчетов остойчивости, а именно при расчетах площади под ДСО используется в случаях:

Правило 1 – 141, которое примет вид 14241 – для расчета площади от 0 до 40

Правило 2 – 1331 – для расчета площади от 0 до 30

Правило 3 – 58 – в комбинации с правилом 2 – для расчета площади от 0 до 50

Так как график ДСО имеет значения в МЕТРАХ и ГРАДУСАХ а площадь под ДСО нам нужно в метр/радиан то шаг диаграммы h делим на 57,3 тем самым переводя градусы в радианы и результат (значение площади) получится в метр/радиан

Как расширять формулы Симпсона на примере Правила 1 – 141

Расчеты по правилам Симпсона

Рассмотрены следующие расчеты:

1.Правило 1 – 141, которое примет вид 14241 – для расчета площади от 0 до 40

2.Правило 2 – 1331 – для расчета площади от 0 до 30

3.Правило 3 – 58 – в комбинации с Правилом 2 – для расчета площади от 0 до 50

4.Правило 1 в комбинации с Правилом 2 – для расчета площади от 0 до 50

Пункты 1, 2, 3 рассмотрены в видео – Using_Simpson’s_Rules_to_Calculate_Dynamical_Stability (папки смартфона)

Пункт 4 рассмотрен в видео – Ship Stability – Combining Simpson’s First and Second Rule to calculate area (Steering Mariners в папке смартфона)

1. Методы расчета критериев остойчивости судна

По
требованиям ИМО остойчивость
судна по критерию погоды «К» считается
достаточной, если площадьсектора«а»
(DGH)
меньше или равна площади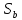сектора«b»
(DEF),
т.е.

Смысл
критерия погоды К
прост:
он позволяет убедиться, что запас энергии
восстанавливающего момента
в
данном случае загрузки судна при крене
до 50° не менее затрат энергии кренящего
моментапри
совместном действии на судно постоянного
ветра, шквала и бортовой качки.

Очевидно,
что ИМО
не требует вычислять величину критерия
погоды «К», а для проверки его соответствия
достаточно провести простое сравнение
площадей “a
“ и ”b”
секторови.

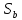
Поэтому
остойчивость судна по критерию погоды
«К»

может быть проверена графически,
аналитически или приближенным
интегрированием по правилам Симпсона
или трапеций.

Рассмотрим
и сравним методы, для чего используем
рис 6.5.

Рис.6.5.
Определение площадей секторов «а»
и
«в»
и
критерия «К»

1.Наиболее
простым и наглядным является графический
метод наложения
площадей;
для чего на фигуре DEF(площадь
сектора «b»)
методом подбора проводится вертикальная
прямая H₁G₁,
отсекающая фигуру DH₁G₁,
по площади равновеликая фигуре DGH(площадь
сектора «а»).
Становится очевидно , что площадь
«b»больше
площади «а»,
т.е. критерий погоды K=
b/a
>
1выполнен и остойчивость судна обеспечена
(рис.6.5.)

2.
Для получения точного значения критерия
«К»
можно использовать графическую
аппроксимацию площадей
секторов площадями равновеликих
прямоугольных треугольников.

Для
этого, как показано на рис.6.5 кривую
линию DF
заменим
прямой
,
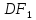
соблюдая равенство площади «b»
сектора DEF
и площади прямоугольного треугольника. При необходимости также можно
преобразовать площадь «а»
сектора DGH
в
площадь прямоугольного треугольника
путем замены кривойDH
прямой. Тогда площади «а»
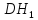
и «b»
можно достаточно точно вычислить, как
площади прямоугольных треугольников
ипо
формулам:

Критерий
погоды будет равен:

(6.6)

Очевидно,
что с помощью линейки легко измерить
длины отрезков
,и по формуле (6.7) рассчитать точное
значение «К».

3.
Рассмотрим аналитический
метод
расчета критерия погоды «К»,
дающий его точное значение.

В
этом случае площади «а»
и «b»
находят по формулам с помощью ДСО
и ДДО:

,
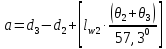
м

,
м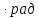(6.7)

где– угол крена от постоянного ветра, град.,

–
угол крена от шквального ветра, град.,

–
угол крена навстречу ветру, град.,

–
угол крена при бортовой качке, град.,

–
плечо ДСО от постоянного ветра, м,

–
плечо ДСО от шквального ветра, м,

–
плечо ДДО при

–
плечо ДДО при

–
плечо ДДО при

В
этом случае величины плеч и площадей и
,
и,«а»
и «в»
определяют
по ДСО
и
ДДО,
как показано на рис 6.6.

Рис.6.6.
Определение площади секторов «а»
и «в»
и
,и

В
основу этого метода положено вычисление
площадей секторов «а»
и «b»
путем нахождения полной площади под
ДСО
и вычитания из нее не входящих в «b»
площадей треугольника
и
прямоугольника со сторонамиии площади «а»,
состоящей из площадей по ДСО
и прямоугольника со сторонамииза вычетом площади треугольника.

Метод
3 дает точное значение критерия погоды
«К»,
но требует построения ДДО
и
сложных вычислений с использованием
многочисленных плеч и углов, поэтому
его целесообразно использовать при
расчетах на компьютере.

4.
Расчет критерия погоды «К»
и
критериев
иможно
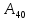
выполнить иметодами
приближенного интегрирования по правилам
трапеций, Симпсона и других.

Расчеты
по этим правилам требуют деления каждой
площади на ряд участков по углу крена,
загромождая диаграммы линиями деления,
а затем величину каждой линии надо
определить и вписать в таблицу. После
этого с учетом специальных коэффициентов
и длины участков деления надо произвести
расчет в табличной форме. Такие расчеты
по точности эквивалентны аналитическому
(3) и графическому (2) методу, но по
трудоемкости и сложности значительно
их превосходят. Этот метод целесообразен
при расчетах на компьютере.

Вывод

Очевидно,
что при оценке остойчивости судна в
учебном процессе наиболее
просты
и наглядны графические способы (1-й
приближенный и 2-й точный).
Менее нагляден и более
трудоемок аналитический метод 3- й
(точный). Наиболее трудоемкими и
громоздкими являются методы приближенного
интегрирования по
правилам
Симпсона и трапеций,
и их применение в курсовых и дипломных
работах нецелесообразно без помощи
компьютера.

Для
вычисления критериев
,
и
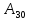
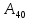
наиболее целесообразно при расчете
ординат
ДСО
вычислить эти площади под диаграммой
ДСО,
как ординаты ДДО,
что показано в таблице 6.4

Соседние файлы в предмете Теория и устройство судна

• #
• #
• #
• #
• #
• #

УДК
629.5.012.014

Даник А. В.

ОПРЕДЕЛЕНИЕ ЗАПАСА ПОПЕРЕЧНОЙ

ДИНАМИЧЕСКОЙ ОСТОЙЧИВОТИ СУДНА ПРИ
ПЕРЕВОЗКЕ ЗЕРНА С ПОМОЩЬЮ ДИАГРАММЫ
СТАТИЧЕСКОЙ ОСТОЙЧИВОСТИ РАЗЛИЧНЫМИ
МЕТОДАМИ

Остойчивость судна при перевозке
зерна регламентируется Международным
кодексом по безопасной перевозке зерна
насыпью, являющейся Главой VI
часть «С» конвенции СОЛАС 1974. Суда,
перевозящие зерновые грузы насыпью
должны быть снабжены информацией об
остойчивости судна при перевозки зерна.
Суда, не имеющие такой информации, должны
грузится по требованиям Международным
кодексом по безопасной перевозке зерна
насыпью или правилам страны погрузки.

Ключевые слова: запас
остойчивости, статический угол крена
от смещения, динамическая поперечная
остойчивость, диаграмма, поперечное
смещение зерна.

Основные требования кодекса по безопасной
перевозке зерна навалом к судам
перевозящие зерно насыпью:

– метацентрическая высота на весь
период рейса с поправками на влияние
свободной поверхности жидкости в танках
должна быть не менее чем 0,3 м;

– угол крена от смещения зерна не должен
превышать 12^о;

– на диаграмме статической остойчивости
(далее ДСО) чистая (остаточная площадь)
между кривой кренящего и восстанавливающего
моментов от 12^о до угла крена 40^о,
или угла заливания если он меньше 40^о,
при всех условиях загрузки, должна быть
не менее 0,075 м.рад.

Запас поперечной динамической
остойчивости. Чем является остаточная
площадь статической остойчивости при
смещении зерна? Она является запасом
поперечной динамической остойчивости
судна под действием кренящего момента,
обозначенный на диаграмме U_θ(θ₃)
(рис.1).

Запас поперечной динамической измеряется
величинами

.

На ДСО изображается площадью, ограниченной
графиками m_θ(θ)
и l_θ(θ₃)
и осью углов крена между θ = 0 и θ₃.
если судно находится по действием
кренящего момента, имея статический
угол крена θ_ст, его запас динамической
остойчивости изображается площадью
между графиками m_θ(θ)
и m_кр(θ)[1].
Определение запаса динамической
остойчивости, т.е. остаточной площади
ДСО будет рассмотрено ниже.

Определение остаточной площади ДСО
при помощи вспомогательной линии. Данный
метод предложенный Аксютиным Л. Р.
(ОВИМУ им. Ленинского комсомола ныне
ОНМА) производят так, как показано на
рис. 1.

Рис.1.
Запас
динамической остойчивости судна,
находящегося под действием кренящего
момента

Для приближенного вычисления расчетной
площади диаграммы S_gs
в м рад. используют следующий прием. На
рис. 2 визуально
проводят вспомогательную линию КМ,
исходя из равенства заштрихованных
помещений, определенного глазомерным
путем. После этого вычисление расчетной
площади производят по формуле

,

где KL и MN – отрезки, измеренные
в мм;

m – масштаб по оси абсцисс, 1
рад.;

n – масштаб по оси ординат, 1
рад.

Рис.
2. Метод
определения остаточной площади ДСО с
помощью построения вспомогательной
линии

Определение остаточной площади ДСО
при помощи палетки. На
ДСО (см. рис.3), построенный в масштабе
плеч, по оси абсцисс откладываем угол
статического крена 12^о, получаемый
от пересыпания зерна, и из точки Г
восстанавливаем перпендикуляр до
пересечения с кривой ДСО – точка Б.
Из точки Б проводим горизонтальную
прямую на ось ординат, точка А.
Отрезок 0А соответствует величине
приведенного плеча кренящего момента
ℓ_кр от пересыпания зерна до угла
12^о, т.е. 0А = ℓ_кр.

Рис.
3. Метод
определения остаточной площади ДСО при
помощи палетки

Из точки С, соответствующей углу
крена 40^о, восстанавливаем
перпендикуляр и откладываем на нем
отрезок СВ, равный 0,8 · ℓ_кр
(СВ = 0,8 · ℓ_кр = cos40^о
· ℓ_кр).

Соединяем прямой линией точки А и
В. Площадь ДСО, заключенная между
ЕДВ и есть нормируемая остаточная
площадь ДСО.

Величину остаточной площади ДСО
рассчитывают с помощью палетки, разграфив
ее прямоугольниками выбранного масштаба,
и подсчитав площадь одного из
прямоугольников.

Например, в нашем случае, в правом верхнем
углу показан прямоугольник, высота
которого равна с учетом масштаба ДСО,
а = 0,05 м, его длина в = 5^о =
0,087 рад. Вся площадь этого прямоугольника
в принятом масштабе равна

Зная площадь одного такого прямоугольника,
с помощью палетки, определим остаточную
заштрихованною площадь ДСО
[3].

Определение остаточной площади ДСО
при помощи приближенной (упрощенной)
формулы. Приближенная
формула по определению остаточной
площади ДСО выглядит следующим образом

,

где ℓ_кр – кренящее плече от
статического смещения зерна;

ℓ_ст – ордината ВС (рис.
4) ВС = ℓ_ст – ℓ_кр∙0,8 (м);

θ_ст – статический угол крена от
смещения зерна в нашем случае этот угол
для примера равен 12^о (в точке
пересечения АВ с ДСО) (град.);

BD – разница между ординатой
40^о и ординатой в точке пересечения
прямой АВ с ДСО в точке D
(град.) [3].

Рис.
4. Метод
определения остаточной площади ДСО

Определение остаточной площади ДСО
по методу Симсона. Наиболее точным
методом по определению площади диаграммы
является метод Симсона или так называемые
«Правила Симсона» [4],
которые упрощают метод определения
остаточной площади ДСО.

Например: Расчет остаточной площади
ДСО под кривой от угла крена 6^о до
угла 40^о. Для данного примера надо
использовать коэффициенты 14241 согласно
метода Симсона. Для чего сначала
определяем интервал между ординатами
для снятия значений ℓ_ст для этих
ординат по формуле

,

для нашего примера

.

Площадь под кривой определяется по
следующей формуле

,

для нашего примера

м.рад.

После чего через найденный интервал
снимаем значения ℓ_ст ДСО (рис.5),
и заносим в табл.1.

Рис.5.
Метод определения остаточной площади
ДСО по методу Симсона

Таблица 1

Расчет площади под
кривой ДСО

Угол крена θо	Плечи ДСО ℓст	Множитель	Результат
6	0,12	1	0,12
14,5	0,32	4	1,28
23	0,55	2	1,10
31,5	0,75	4	3,00
40	0,86	1	0,86
		Σ	6,36

Далее определяем площадь под трапецией

Рис.6.
Метод определения площади трапеции

а ­– ордината соответствующая углу
θ_ст, для нашего примера 6^о
(ордината равна 0,102 м.);

b – ордината соответствующая
углу θ_f, для нашего
примера 40^о (ордината равна 0,102 м).

Площадь трапеции определяется по формуле

,

для нашего примера

м.
рад.

Остаточная площадь равна

м.рад.,

что больше чем 0,075 м.рад [4].

В данной статье были рассмотрены наиболее
известные и простые (не требующие
большого количества времени и «громоздких»
расчетов) методы по определению запаса
динамической поперечной остойчивости,
т.е. остаточной площади под кривой ДСО.

Вывод: при любом варианте загрузки
зерном неповрежденное судно должно
соответствовать вышеперечисленным
критериям остойчивости коим является
расчет запаса остойчивости, т.е. остаточной
площади ДСО.

ЛИТЕРАТУРА

1. Справочник по
   теории корабля. Под редакцией В.
   Ф. Дробленков, А. И. Ермолаев, Н. П. Муру,
   С. И. Крылов, Ю. И. Кузнецов.
   М.: Воениздат, 1984. – 589
   с.

2. Аксютин Л.Р.
   Грузовой план морского судна. Одесса:
   Латстар, 1999. – 139
   с.

3. Мельник В.Н.
   Эксплуатационные расчеты мореходных
   характеристик судна/ М.: Транспорт,
   1990. –144
   с.

4. Captain
   D.R. Derret, Dr. C. B. Barras.
   Ship stability for Master and Mates. Fifth
   edition
   Oxford.:
   Publishing
   house “Butterworth
   Heinimann”,
   2001.

В процессе плавания судна часто возникает необходимость в дополнительном контроле остойчивости вследствие расхода запасов, топлива, проведении балластных операций. Для этого существуют практические методы расчёта мореходных качеств судна. Основная величина, с помощью которой проверяется остойчивость – метацентрическая высота. Наиболее удобно определить метацентрическую высоту можно по периоду бортовой качки по формуле:

GM = ;

где с – коэффициент, зависящий от типа судна и его загрузки, обычное значение для

грузового судна равняется 0,78;

В – ширина судна, (м);

Т0 – период бортовых колебаний, (сек). Для получения значения Т0 измеряют не менее 10 колебаний судна и рассчитывают среднее значение.

Если на судне имеются большие свободные поверхности жидких грузов или значение GM менее 0,2 метров, тогда результаты расчёта, полученные с помощью указанной формулы, оказываются ненадёжными.

Расчет и построение диаграмм остойчивости ДСО и ДДО

Диаграмма статической остойчивости называется кривая зависимости восстанавливающего момента от угла крена. Согласно Правилам Регистра ДСО строят для каждого из расчётных случаев нагрузки судна. ДСО позволяет решить следующие задачи:

1) найти величину кренящего момента от смещения груза и опрокидывающего момента;

2) создание необходимого обнажения борта, необходимого для осуществления ремонта корпуса, забортной арматуры;

3) определение наибольшей величины статически приложенного кренящего момента, который может выдержать судно не опрокидываясь, и крена, который она при этом получит;

4) определение угла крена судна от мгновенно приложенного кренящего момента при отсутствии начального крена;

5) определение угла крена судна от мгновенно приложенного кренящего момента при наличии начального крена по направлению действия кренящего момента;

6) определение угла крена судна от мгновенно приложенного кренящего момента при наличии начального крена в противоположном направлении действию кренящего момента;

7) определение угла крена при перемещении груза по палубе;

8) определение статического опрокидывающего момента и угла статического опрокидывания;

9) определение динамического опрокидывающего момента и угла динамического опрокидывания;

10) определение необходимого кренящего момента для спрямления судна;

11) определение веса груза, при перемещении которого судно потеряет остойчивость;

дальнейшие необходимые операции по улучшению остойчивости судна. Диаграмма строится для полного суждения об остойчивости. В «Информации об остойчивости» даются конкретные указания, как это лучше всего сделать, например, используя следующую формулу:

GZ= KN- ZG(суд.кор)•sin(Fi) (м);

где GZ – плечё статической остойчивости;

ZG(суд.кор) – вертикальная составляющая ЦТ судна, исправленная поправкой на влияние свободной поверхности;

KN – интерполяционные кривые остойчивости, пантокарены;

Fi – угол крена судна.

Для произведения подсчётов в соответствии с приведённой формулой в «Информации об остойчивости» в таблице – 4.10 представлены численные значения KN (м) для различных углов крена в зависимости от водоизмещения судна. Необходимо отметить что «Информация об остойчивости» обозначено замечание, что при подсчёте остойчивости судна для всех случаев загрузки судна судно не имеет начального наклонения, т.е. судно «сидит» на ровном киле (trim = 0 m).

Таблица 4.10 – Пантокарены

V (m3)	KN (m)
100	200	300	400	500	600	700	800	900
340	1,256	2,568	3,800	4,867	5,679	6,110	6,236	6,110	5,749

GZ(100) = KN(100)- ZG(суд.кор)•sin(100) = 1,256 – 6,688• sin(100) = 0,0946 (м);

GZ(200) = KN(200)- ZG(суд.кор)•sin(200) = 2,568 – 6,688• sin(200) = 0,2806 (м);

GZ(300) = KN(300)- ZG(суд.кор)•sin(300) = 3,800 – 6,688• sin(300) = 0,456 (м);

GZ(400) = KN(400)- ZG(суд.кор)•sin(400) = 4,867 – 6,688• sin(400) = 0,5680 (м);

GZ(500) = KN(500)- ZG(суд.кор)•sin(500) = 5,679 – 6,688• sin(500) = 0,5557 (м);

GZ(600) = KN(600)- ZG(суд.кор)•sin(600) = 6,110 – 6,688• sin(600) = 0,3180 (м);

GZ(700) = KN(700)- ZG(суд.кор)•sin(700) = 6,236 – 6,688• sin(700) = -0,0486 (м);

GZ(800) = KN(800)- ZG(суд.кор)•sin(800) = 6,110- 6,688•sin(800) = -0,4763 (м);

GZ(900) = KN(900)- ZG(суд.кор)•sin(900) = 5,749- 6,688• sin(900) = -0,9390 (м).

Построенную диаграмму статической остойчивости можно найти в приложении Б. Одним из наиболее важным критериев достаточной остойчивости судна, который может быть найден с помощью ДСО, является плечо кренящего момента, из-за воздействия бокового ветрового давления при соответствующем угле крена. Данное значение находится по формуле с дальнейшим откладыванием его на оси GZ диаграммы статической остойчивости и нахождением угла крена.

hkw= (м) ;

где hkw – плечо кренящего момента из-за давления ветра при угле крена Fi; pw – боковое ветровое давление = 1,0 (кН/м2); А – боковая площадь парусности судна выше ватерлинии, найденная по диаграмме «Сумм ветрового действия» по значению средней осадки dm и равное 930 (м2); lw – дистанция от ватерлинии до центра парусности судна. Находится из той же таблицы по тем же значениям, и равна 7,4 (м); D – весовое водоизмещение судна, равное 5501,58 (т); dm – средняя осадка, равная 4,95 (м); Fi – данный угол крена.

Для построения дополнительной диаграммы hkw=f(Fi) и нахождения статического угла крена вычислим значение hkw для следующих углов: 00, 50, 100, 150.

Тогда:

hkw(00)==0,017•9,875•1=0,168(м);

hkw(50)==0,017•9,875•0,991=0,166 (м);

hkw(100)==0,017•9,87•0,97=0,162(м);

hkw(150)==0,017•9,88•0,93=0,155(м).

Т.о. в результате пересечения графиков hkw = f(Fi) и GZ = f(Fi) получаем значение статического угла крена равное Fi =13,5 . В соответствии с требованием Регистра судоходства Fi< = 180, именно этому требованию удовлетворяют наши расчёты (график смотри в приложении А). Далее с помощью ДСО подсчитаем значение начальной метацентрической высоты:

GM=KM- ZG ;

где GM – начальная метацентрическая высота;

KM – отстояние метацентра от киля. Находится из числовых таблиц, приведённых в «Информации» и выбирается в соответствии со значением D и dm. КМ = 7,137 (м); ZG – координаты вертикальные центра тяжести, равная

Тогда:

GM= 7,137 – 6,674 = 0,463 (м);

GMk= GM – dGM;

где GMk – начальная метацентрическая высота исправленная поправкой на влияние свободной поверхности, (м);

dGM – коэффициент коррекции для свободной поверхности, (т•м); Тогда:

GMk = 0,463 – 0,0144 = 0,4486 (м) .

Необходимо отметить, что характеристика бортовой качки судна зависит напрямую от метацентрической высоты. Чем больше это значение, тем качка наблюдается более резкая, интенсивная, что отрицательно влияет на крепление груза и его целостность, а в целом и на безопасность всего судна.

Кривая зависимости работы восстанавливающего момента от угла крена называется диаграмма динамической остойчивости. Диаграмма можно и не строить, если начальная остойчивость судна удовлетворяет предъявляемым требованиям, но для определения некоторых параметров остойчивости судна удобно пользоваться именно этой диаграммой. Построим ДДО по следующему способу.

В таблице 4.11 указываю плечи динамической остойчивости GZd и построить график заполняется нижеследующая таблица:

Таблица 4.11 – Плечи динамической остойчивости

Плечо	Fi
00	100	200	300	400	500	600	700	800	900
GZ	0	0,0946	0,2806	0,456	0,5680	0,5557	0,3180	-0,0486	-0,4763	-0,9390
?	0	0,0946	0,4698	1,2064	2,2304	3,3541	4,2278	4,4972	3,9723	2,557
GZd	0	0,008	0,04	0,105	0,195	0,292	0,368	0,392	0,346	0,223

Построенную диаграмму динамической остойчивости можно найти в приложении Б. С помощью ДСО согласно правилам Регистра Судоходства Украины судно признаётся достаточно остойчивым, если выполняется следующее требование по критерий погоды:

;

где К – критерий погоды;

Мопр – минимальный опрокидывающий момент, т•м;

Мкр – кренящий момент от действия ветра, т•м. Кренящий момент от действия ветра находим по формуле:

;

где ?w???условное расчётное давление ветра, равное 1.0 кН/м2;

А – площадь парусности судна соответствующая данной загрузке судна, равная 930 м2;

lw – расстояние от ватерлинии до центра парусности судна.

Тогда: т•м. Опрокидывающий момент находится с помощью плеча кренящего момента, из-за воздействия бокового ветрового давления при максимальном статическом угле крена в 13,50, по формуле:

Мопр=hkw(13,5)•D=(pw•A/10)•(lw+dm/2)•(0,25+0,75•cos3Fi) (4.2.3.7);

Мопр =(1•930/10•5501,58)•(7,4+4,95/2)•(0,25+0,75• cos3(13,5))= 0,017•9,875•0,939= 863,74(м);

Тогда:

– удовлетворительный критерий погоды.

Проверка остойчивости по требованиям Регистра Судоходств Украины

Регистр Судоходства Украины устанавливает следующие нормы остойчивости, предъявляемые к судну:

максимальное плечо статической остойчивости ДСО должно быть: – GZ =>0,25 м. при максимальной длине судна 80 м; – GZ =>0,20 м. при длине судна более 100 м;

1) угол максимума диаграммы должен быть более или равен 300;

2) угол заката ДСО должен быть более или равен 600 и 550 с учётом обледенения.

3) критерий погоды К должен быть более или равен 1, а при плавании в северной Атлантике должен быть более или равен 1,5;

4) исправленная поперечная метацентрическая высота GMk для всех вариантов загрузки должна быть всегда положительной. Ориентировочное значение оптимальной метацентрической высоты для сухогрузных судов лежит в пределах от 0,3 до 1,0 м.

Проверка остойчивости по требованиям ИМО в соответствии с резолюцией А.167 (ES.IV)

Международная Морская Организация устанавливает следующие нормы остойчивости, предъявляемые к судну:

1) минимальная поперечная метацентрическая высота GMk, откорректированная коэффициентом влияния свободной поверхности не должна быть менее чем 0,15 м.;

2) плечо статической остойчивости не должно быть менее 0,20 м. при угле крена равному или большему чем 300;

3) максимальное значение плеча статической остойчивости на ДСО не должен быть менее 250;

4) площадь, находящаяся под ДСО до 300 крена не должна быть менее 0,055 m•rad;

5) площадь, находящаяся под ДСО до 400 крена не должна быть менее 0,09 m•rad;

6) разность площадей, находящихся между 300 и 400 крена не должна быть менее чем 0,03 m•rad;

7) критерий погоды должен быть более или равен 1;

дополнительный угол крена от действия ветра должен быть не более 180 или должен быть равен 80% от угла, при котором кромка палубы входит в воду, в зависимости от того, какой угол минимальный. Для того, чтобы сравнить полученные значения с требуемыми составляется таблица-4.13 отображающая значения расчётных величин:

Таблица 4.13 – Суммарная таблица полученных данных

GZ max (м)	Fi max	Fi зак.	К	GMk (м)	Fi(300) (м)	S(300) (m•rad)	S(400) (m•rad)	?S	Крен от ветра
0,568	450	660	1,25	0,45	0,456	0,055	0,09	0,03	13,50

В соответствии с выше перечисленными условиями данный вариант загрузки придаёт судну оптимальную остойчивость, и она соответствует требованиям, как Регистра Судоходства Украины, так и требованиям Международной Морской Организации.