1.3. Как найти площадь плоской фигуры
с помощью двойного интеграла?
Двойной интеграл ![]() численно
численно
равен площади плоской фигуры ![]() (области интегрирования). Сначала рассмотрим задачу в общем
(области интегрирования). Сначала рассмотрим задачу в общем
виде.
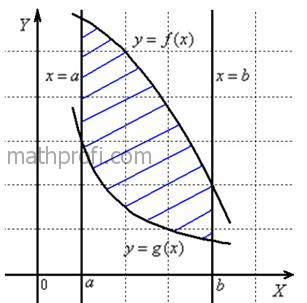
А именно вычислим площадь фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() . Для определённости считаем, что
. Для определённости считаем, что ![]() на отрезке
на отрезке ![]() .
.
Площадь заштрихованной фигуры численно равна ![]() , и сейчас мы «раскрутим» тему.
, и сейчас мы «раскрутим» тему.
Выберем первый способ обхода области:
![]()
Таким образом: 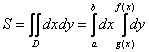
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний
интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую «чайникам», да и не только им. Потому что это
удобно.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
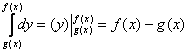
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь
разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную
функцию) верхний предел, затем – нижний предел
2) Результат первого пункта нужно подставить во внешний интеграл:
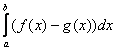
Более компактная запись всего решения выглядит так:
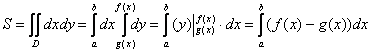
Полученная формула 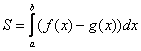 – это в
– это в
точности рабочая формула для вычисления площади плоской
фигуры с помощью обычного определённого интеграла!
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с
помощью определённого интеграла!
Пример 9
С помощью двойного интеграла, вычислить площадь фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: изобразим область ![]() на чертеже:
на чертеже:
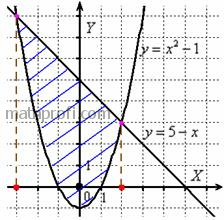
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Выберем следующий порядок обхода области (1-й способ):
![]()
Здесь и далее я не буду останавливаться на том, как выполнять обход, т.к. выше были приведены очень подробные
разъяснения.
Таким образом:
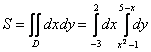
Как уже отмечалось, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду
придерживаться и я:
1) Сначала разбираемся с внутренним интегралом:
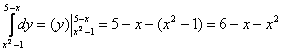
Здесь мы ВМЕСТО «игрек» сначала подставили верхний предел интегрирования ![]() , а затем – нижний:
, а затем – нижний: ![]() . Если вы запамятовали формулу Ньютона-Лейбница, обязательно
. Если вы запамятовали формулу Ньютона-Лейбница, обязательно
найдите её в приложениях! На всякий случай я приложил к данному курсу Справку по интегралам и
Справку по производным.
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
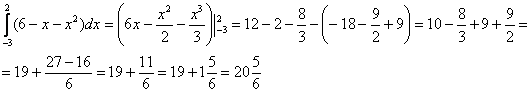
Пункт 2 – это фактически нахождение площади плоской фигуры с
помощью определённого интеграла. Обо всех тонкостях решения этой задачи (а их немало) можно ознакомиться по ссылке
выше либо в курсе Определённые и несобственные интегралы.
Это китайское напоминание.
Ответ: ![]()
Несмотря на то, что эту задачу мы неоднократно решали ранее, здесь ещё есть о чём поговорить.
Любопытное задание для самостоятельного решения:
Пример 10
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]()
Примерный образец чистового оформления задачи в конце книги.
В двух предыдущих примерах значительно выгоднее использовать первый способ
обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если
не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в
заключение курса молодого «ботана» рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: нас с нетерпением ждут две параболы, которые «лежат на боку». Улыбаться не нужно, похожие вещи в
кратных интегралах встречаются частенько.
Представим параболу ![]() в
в
виде двух функций:
![]() – верхняя ветвь и
– верхняя ветвь и ![]() – нижняя ветвь.
– нижняя ветвь.
Аналогично, представим параболу ![]() в виде верхней
в виде верхней ![]() и нижней
и нижней ![]() ветвей.
ветвей.
Графики строим поточечно, причём, по причине симметрии, вычислений у нас в два раза меньше. В результате получается вот
такая причудливая фигура:
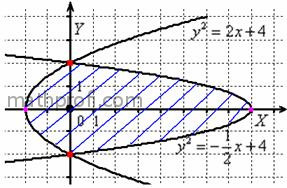
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Что будет, если мы выберем первый способ обхода области? Во-первых,
данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 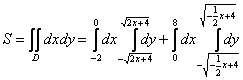 (следим по чертежу!!!). Интегралы, конечно,
(следим по чертежу!!!). Интегралы, конечно,
не «убийственные», но… есть старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
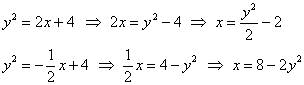
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без
всяких там веток, корней и прочего дерева.
И, согласно второму способу, обход области будет следующим:
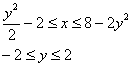
Таким образом:
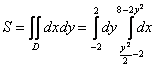
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
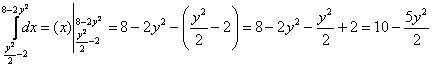
Результат подставляем во внешний интеграл:
2) 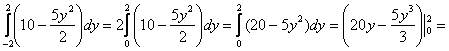
![]()
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней.
Также обратите внимание на первый шаг: подынтегральная функция ![]() является чётной, а отрезок интегрирования симметричен относительно
является чётной, а отрезок интегрирования симметричен относительно
нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Что добавить…. Всё!
Ответ: ![]()
Для проверки своей техники интегрирования можете попробовать вычислить 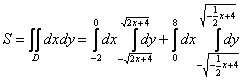 . Ответ должен получиться точно таким же.
. Ответ должен получиться точно таким же.
Пример 12
С помощью двойного интеграла, вычислить площадь плоской фигуры, ограниченной линиями ![]()
Это пример для самостоятельного решения. Интересно отметить, что если вы попробуете использовать первый способ обхода
области, то фигуру придётся разделить уже не на две, а на три части! И, соответственно, получится три пары повторных
интегралов. Бывает и такое.
Итак, начальный мастер-класс подошёл к завершению, и пора переходить на гроссмейстерский уровень. Обязательно с хорошим
настроением! – оранжевым настроением – прямо как сейчас у меня, а почему оно такое, я объясню чуть позже:
 1.4. Как вычислить произвольный двойной интеграл?
1.4. Как вычислить произвольный двойной интеграл?
 1.2.1. Как изменить порядок обхода области?
1.2.1. Как изменить порядок обхода области?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Разберем готовые ответы к примерам на нахождение площади плоской фигуры, которая ограничена кривыми через двойные интегралы.
Задание не сложные, а вся схема нахождения площади требует всего трех вещей:
знание элементарных функций и умение искать точки их пересечения;
понимание как через криволинейные интегралы искать площадь, умение правильно расставлять пределы;
хорошых знаний теории вычисления интегралов, поскольку к этому все сводится.
ЗАДАНИЕ 4.1 Найти площадь плоской фигуры, которая образована линиями:
x=4-y2, x+2y=4.
Решение: Фигура ограничена x=4-y2 – параболой с вершиной в точке O(4;0) и ветками влево;
но x+2y=4 – прямой, которая отрезается на осях в точках (4;0) и (0;2).
Найдем точки пересечения графиков функций из системы уравнений:
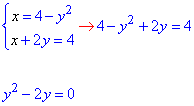
При ее решении получим две точки
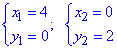
График параболы и прямой приведен на рисунку
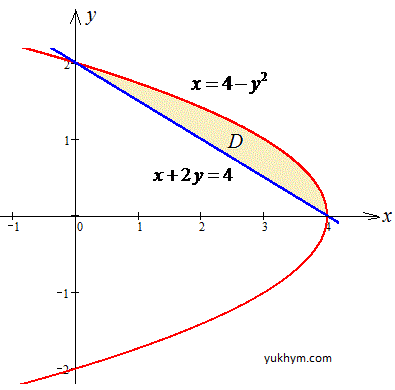
Запишем пределы интегрирования:
D: 0≤x≤4, 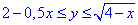
Здесь имеем y=√(4-x) – уравнение верхней части параболы x=4-y^2;
Вычислим площадь фигуры нахождением двойного интеграла:
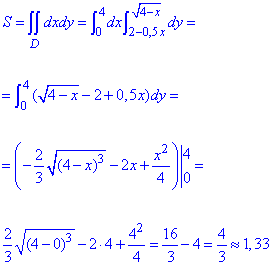
Площадь равна 1,33 единиц квадратных.
ЗАДАНИЕ 4.2 Найти площадь плоской фигуры, которая образована кривыми:
y=2-x, y2=4x+4.
Решение: y^2=4x+4 – парабола с вершиной в точке O (-1;0) и ветками вправо;
y=2-x, x+y=2 – прямая, которая отрезается на осях в точках (2;0) и (0;2).
Складываем систему уравнений для нахождения точек пересечения графиков заданных кривых:
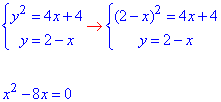
При решении получим две точки
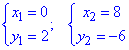
График области интегрирования имеет вид
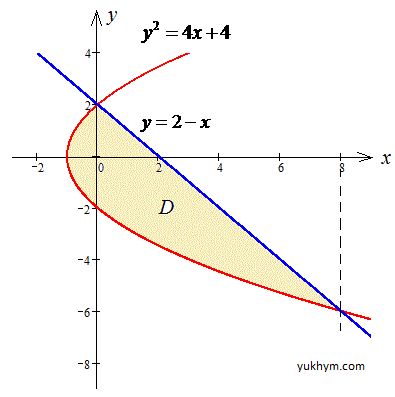
Пределы в области D:
-6≤x≤2, 0,25y2-1≤y≤2-y.
Находим площадь фигуры через криволинейный интеграл:
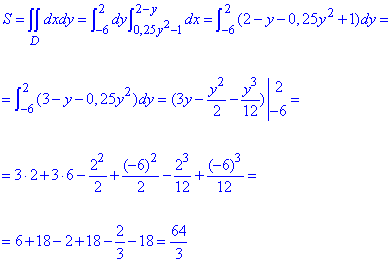
Кратный интеграл не трудно интегрировать.
ЗАДАНИЕ 4.3 Найти площадь плоской фигуры, которая образована линиями:
x2+y2=4, x2+y2=4x.
Решение: Область интегрирования ограничена x2+y2=4 – кругом с центром в точке O1(0;0) и радиусом R=2;
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 – круг с центром в точке O1(2;0) и радиусом R=2.
Найдем точки пересечения графиков заданных функций из системы уравнений:
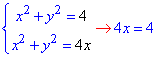
отсюда
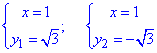
График фигуры, площадь которой ищем приведен на рисунку
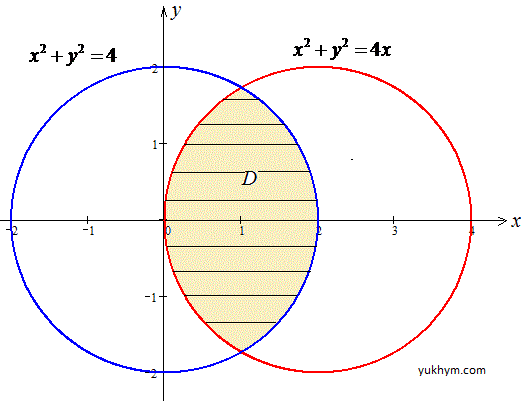
Расставим пределы в области D
(поскольку область симметрична относительно прямой y=0, то будем рассматривать ее половину, а результат умножим на 2):
D: 0≤y≤√3, 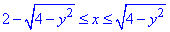
Здесь записали:
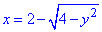 – уравнение левого полукруга (x-2)2+y2=4;
– уравнение левого полукруга (x-2)2+y2=4;
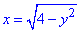 – уравнение правого полукруга x2+y2=4.
– уравнение правого полукруга x2+y2=4.
Вычислим площадь фигуры через двойной интеграл:
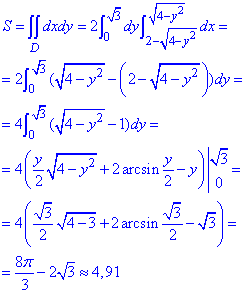
При интегрировании получили арксинусы, дальше подставили пределы интегрирования и округлили конечные значения.
ЗАДАНИЕ 4.4 Найти площадь плоской фигуры, которая образована кривыми:
x2+y2=2x, x2+y2=4x, y=x, y=0.
Решение: Начнем вычисление с анализа того, что собой представляет фигура, площадь которой нужно найти.
Сведем уравнения к простому виду
x2+y2=2x, x2-2x+1 +y2=1, (x-1)2+y2=12 – круг с центром в точке O1(1;0) и радиусом R=1.
x2+y2=4x, x2-4x+4+y2=4, (x-2)2+y2=22 – круг с центром в точке O1(2;0) и радиусом R=2.
y=x – прямая, которая является биссектрисой первой и третьей четверти.
Рисунок к задаче илюстрирует площадь которой фигуры нужно найти
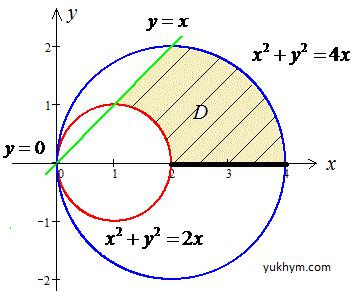
Поскольку поверхность ограничена кругами, то целесообразно перейти к полярным координатам.
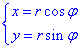
Найдем якобиан перехода:
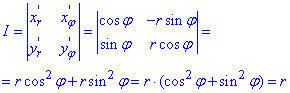
Запишем заданные функции в полярной системе координат:
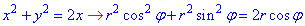
отсюда 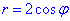
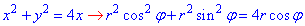
отсюда 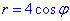
y=0, тогда 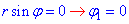
y=x, тогда 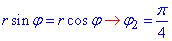
Это нам нужно, чтобы знать пределы в новой системе координат.
Пределы интегрирования в полярной системе координат:
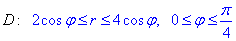
Вычислением кратного интеграла находим площадь фигуры, ограниченной заданными кривыми:
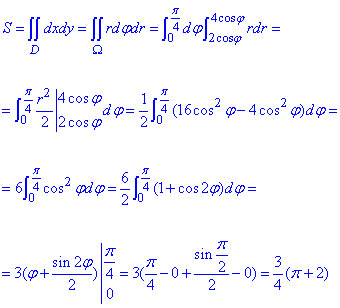
Конечное значение площади можно еще округлить.
Из этого примера Вы ознакомились как искать площадь в полярной системе координат.
В следующей статье разберем еще несколько примеров на нахождение площади фигур интегрированием.
Вычисление площади поверхности с помощью двойного интеграла
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные формулы
Если везде в области $D$ на координатной плоскости $xOy$ для формулы $I=iint limits _{D}fleft(x,yright)cdot dxcdot dy $ положить $fleft(x,yright)equiv 1$, то, в соответствии со своим геометрическим смыслом, двойной интеграл будет численно равен площади $S$ области интегрирования $D$, то есть $S=iint limits _{D}dxcdot dy $. В полярной системе координат эта же самая формула приобретает вид $S=iint limits _{D^{*} }rho cdot drho cdot dphi $.
Пусть некоторая поверхность $Q$ задана уравнениям $z=f_{1} left(x,yright)$. Вычислим площадь той части поверхности $Q$, которая проецируется на координатную плоскость $xOy$ в область $D_{1} $, где функция $f_{1} left(x,yright)$ непрерывна и имеет непрерывные частные производные. Тогда искомую площадь можно вычислить по формуле $S=iint limits _{D_{1} }sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dxcdot dy $.
Если уравнение поверхности $Q$ задано в виде $x=f_{2} left(y,zright)$ или $y=f_{3} left(x,zright)$, то соответствующие формулы для вычисления площади поверхности имеют следующий вид:
Здесь $D_{2} $ и $D_{3} $ — области, в которые проецируется поверхность $Q$ на координатные плоскости $yOz$ и $xOz$ соответственно.
Применение формул на практике
Задача 1
Замкнутая область $D$ на плоскости определяется пересечением параболы $y=2cdot x^{2} -16cdot x+31$ с двумя прямыми в точках $A$ и $B$ при $x_{A} =3$ и $x_{B} =6$ соответственно. Эти прямые, в свою очередь, пересекаются в заданной точхе $Cleft(5,9right)$. С помощью двойного интеграла вычислить площадь области $D$, рассматривая её как правильную в направлении оси $Oy$.
- Находим координаты точки $Aleft(x_{A} ,y_{A} right)$:
- Находим координаты точки $Bleft(x_{B} ,y_{B} right)$:
- Находим уравнение прямой $AC$. Она проходит через точки $Aleft(3,1right)$ и $Cleft(5,9right)$. Её уравнение имеет вид $y=a_{1} cdot x+b_{1} $. Угловой коэффициент: $a_{1} =frac{9-1}{5-3} =4$, смещение $b_{1} =1-4cdot 3=-11$. Окончательно $y=4cdot x-11$.
- Находим уравнение прямой $CB$. Она проходит через точки $Cleft(5,9right)$ и $Bleft(6,7right)$. Её уравнение имеет вид $y=a_{2} cdot x+b_{2} $. Угловой коэффициент: $a_{2} =frac{7-9}{6-5} =-2$, смещение $b_{2} =9-left(-2right)cdot 5=19$. Окончательно $y=-2cdot x+19$.
- Заданная область $D$ является правильной в направлении оси $Oy$. Нижняя граница области образована параболой. Верхняя граница области состоит из двух участков: прямой $AC$ и прямой $CB$. Поэтому область $D$ разбиваем на две подобласти (левую $D_{1} $ и правую $D_{2} $) вертикальной прямой, проходящей через точку $C$.
- Площади подобластей определяем с помощью двойного интеграла $S=iint limits _{D}dxcdot dy $. При этом двойной интеграл для каждой подобласти будем вычислять с помощью двукратного интеграла $S=iint limits _{D}dxcdot dy =int limits _{a}^{b}dxcdot int limits _{phi _{1} left(xright)}^{phi _{2} left(xright)}dy $.
- Находим площадь $S_{1} $ левой подобласти $D_{1} $, которая слева ограничена прямой $x=3$, справа — прямой $x=5$, снизу — параболой $y=2cdot x^{2} -16cdot x+31$, сверху — прямой $AC$, уравнение которой $y=4cdot x-11$. Таким образом, $a=3$, $b=5$, $phi _{1} left(xright)=2cdot x^{2} -16cdot x+31$, $phi _{2} left(xright)=4cdot x-11$. Для вычисления площади $S_{1} $ левой подобласти $D_{1} $ окончательно получаем интеграл $S_{1} =int limits _{3}^{5}dxcdot int limits _{2cdot x^{2} -16cdot x+31}^{4cdot x-11}dy $.
- Сначала вычисляем внутренний интеграл $I_{1} $, в котором интегрирование выполняется по $y$, а $x$ считается постоянной:
- Теперь полученную функцию от $x$ следует проинтегрировать по $x$:
- Находим площадь $S_{2} $ правой подобласти $D_{2} $, которая слева ограничена прямой $x=5$, справа — прямой $x=6$, снизу — параболой $y=2cdot x^{2} -16cdot x+31$, сверху — прямой $CB$, уравнение которой $y=-2cdot x+19$. Таким образом, $a=5$, $b=6$, $phi _{1} left(xright)=2cdot x^{2} -16cdot x+31$, $phi _{2} left(xright)=-2cdot x+19$. Для вычисления площади $S_{2} $ правой подобласти $D_{2} $ окончательно получаем интеграл $S_{2} =int limits _{5}^{6}dxcdot int limits _{2cdot x^{2} -16cdot x+31}^{-2cdot x+19}dy $.
- Сначала вычисляем внутренний интеграл $I_{2} $, в котором интегрирование выполняется по $y$, а $x$ считается постоянной:
- Теперь интегрируем по $x$ полученную функцию от $x$:
- Площадь области $D$ равна $S=S_{1} +S_{2} =10,667+4,333=15$ кв.ед.
$y_{A} =2cdot x_{A}^{2} -16cdot x_{A} +31=2cdot 3^{2} -16cdot 3+31=1$. Получаем $Aleft(3,1right)$.
$y_{B} =2cdot x_{B}^{2} -16cdot x_{B} +31=2cdot 6^{2} -16cdot 6+31=7$. Получаем $Bleft(6,7right)$.
[I_{1} =int limits _{2cdot x^{2} -16cdot x+31}^{4cdot x-11}dy =left[yright]_{2cdot x^{2} -16cdot x+31}^{4cdot x-11} =]
[=left(4cdot x-11right)-left(2cdot x^{2} -16cdot x+31right)=-2cdot x^{2} +20cdot x-42.]
[S_{1} =int limits _{3}^{5}I_{1} cdot dx =int limits _{3}^{5}left(-2cdot x^{2} +20cdot x-42right)cdot dx =]
[=-2cdot int limits _{3}^{5}x^{2} cdot dx +20cdot int limits _{3}^{5}xcdot dx -42cdot int limits _{3}^{5}dx =-2cdot left[frac{x^{3} }{3} right]_{3}^{5} +20cdot left[frac{x^{2} }{2} right]_{3}^{5} -42cdot left[xright]_{3}^{5} =]
[=-2cdot frac{1}{3} cdot left[5^{3} -3^{3} right]+20cdot frac{1}{2} cdot left[5^{2} -3^{2} right]-42cdot left[5-3right]=]
[=-frac{2}{3} cdot 98+10cdot 16-42cdot 2approx 10,667.]
[I_{2} =int limits _{2cdot x^{2} -16cdot x+31}^{-2cdot x+19}dy =left[yright]_{2cdot x^{2} -16cdot x+31}^{-2cdot x+19} =]
[=left(-2cdot x+19right)-left(2cdot x^{2} -16cdot x+31right)=-2cdot x^{2} +14cdot x-12.]
[S_{2} =int limits _{5}^{6}I_{2} cdot dx =int limits _{5}^{6}left(-2cdot x^{2} +14cdot x-12right)cdot dx =]
[=-2cdot frac{1}{3} cdot left[6^{3} -5^{3} right]+14cdot frac{1}{2} cdot left[6^{2} -5^{2} right]-12cdot left[6-5right]=]
[=-frac{2}{3} cdot 91+7cdot 11-12cdot 1approx 4,333.]
«Вычисление площади поверхности с помощью двойного интеграла» 👇
Задача 2
На горизонтальной плоскости $xOy$ находится вертикальное цилиндрическое сооружение. Пол сооружения (область $D$) имеет вид прямоугольника с вершинами $Oleft(0,0right)$, $Mleft(5,0right)$, $Kleft(5,7right)$ и $Nleft(0,7right)$. Крыша сооружения имеет вид купола и описывается уравнением $z=sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } $. Требуется с помощью двойного интеграла вычислить площадь крыши этого сооружения.
- Площадь крыши сооружения вычисляем по формуле $S=int limits _{a}^{b}dxcdot int limits _{phi _{1} left(xright)}^{phi _{2} left(xright)}sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dy $. Здесь $z=sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } $.
- Находим частную производную $frac{partial z}{partial x} $:
- Находим частную производную $frac{partial z}{partial y} $:
- Находим подкоренное выражение интеграла:
- Находим внутренний интеграл:
- Находим площадь крыши:
Его прямоугольный пол является правильным в направлении оси $Oy$. Прямые $x=a$ и $x=b$ ограничивают пол в направлении оси $Ox$ сзади и спереди, следовательно, $a=0$, $b=5$. Линии $phi _{1} left(xright)$ и $phi _{2} left(xright)$ ограничивают пол в направлении оси $Oy$ слева и справа, следовательно, $phi _{1} left(xright)=0$, $phi _{2} left(xright)=7$. Окончательно $S=int limits _{0}^{5}dxcdot int limits _{0}^{7}sqrt{1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} } cdot dy $.
[frac{partial z}{partial x} =frac{partial left(sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } right)}{partial x} =frac{partial sqrt{left(4cdot x+5right)^{3} } }{partial x} =6cdot sqrt{4cdot x+5} .]
[frac{partial z}{partial y} =frac{partial left(sqrt{left(4cdot x+5right)^{3} } +sqrt{left(2cdot y+6right)^{3} } right)}{partial y} =frac{partial sqrt{left(2cdot y+6right)^{3} } }{partial y} =3cdot sqrt{2cdot y+6} .]
[W=1+left(frac{partial z}{partial x} right)^{2} +left(frac{partial z}{partial y} right)^{2} =144cdot x+18cdot y+235.]
Таким образом, для нахождения площади нужно вычислить интеграл
[S=int limits _{0}^{5}dx int limits _{0}^{7}sqrt{W} cdot dy =int limits _{0}^{5}dx int limits _{0}^{7}sqrt{144cdot x+18cdot y+235} cdot dy .]
[I=int limits _{0}^{7}sqrt{144cdot x+18cdot y+235} cdot dy =frac{1}{27} cdot left(144cdot x+361right)^{frac{3}{2} } -frac{1}{27} cdot left(144cdot x+235right)^{frac{3}{2} } .]
[S=int limits _{0}^{5}Icdot dx =frac{1}{27} cdot int limits _{0}^{5}left(144cdot x+361right)^{frac{3}{2} } cdot dx -frac{1}{27} cdot int limits _{0}^{5}left(144cdot x+235right)^{frac{3}{2} } cdot dx ;]
[I_{1} =int limits _{0}^{5}left(144cdot x+361right)^{frac{3}{2} } cdot dx =left[frac{1}{144} cdot frac{left(144cdot x+361right)^{frac{5}{2} } }{frac{5}{2} } right]_{0}^{5} approx 99845,86;]
[I_{2} =int limits _{0}^{5}left(144cdot x+235right)^{frac{3}{2} } cdot dx =left[frac{1}{144} cdot frac{left(144cdot x+235right)^{frac{5}{2} } }{frac{5}{2} } right]_{0}^{5} approx 75938,31;]
окончательно $S=frac{1}{27} cdot left(99845,86-75938,31right)approx 885,46$ кв.ед.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 19.01.2023
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой облас ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»
ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей» 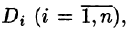 площади которых обозначим через
площади которых обозначим через  а диаметры (наибольшее расстояние между точками области) — через
а диаметры (наибольшее расстояние между точками области) — через 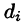 (см. рис. 214).
(см. рис. 214).
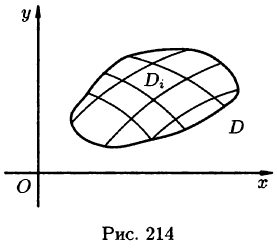
В каждой области  выберем произвольную точку
выберем произвольную точку 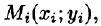 умножим значение
умножим значение 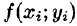 функции в этой точке на
функции в этой точке на  и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
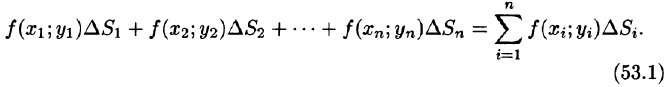
Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 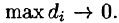 Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
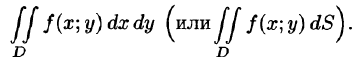
Таким образом, двойной интеграл определяется равенством
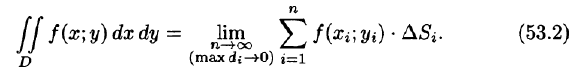
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
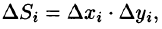 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде
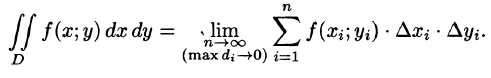
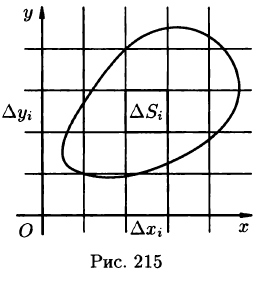

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
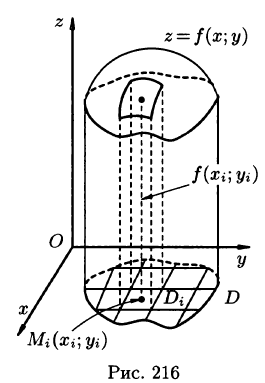
Рассмотрим тело, ограниченное сверху поверхностью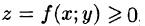 , снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей
, снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей  , площади которых равны A
, площади которых равны A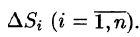 Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием
Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием  через
через 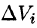 , получим
, получим
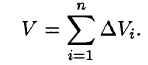
Возьмем на каждой площадке Di произвольную точку 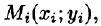 и заменим каждый столбик прямым цилиндром с тем же основанием
и заменим каждый столбик прямым цилиндром с тем же основанием  и высотой
и высотой 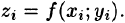 Объем этого цилиндра приближенно равен объему
Объем этого цилиндра приближенно равен объему 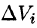 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 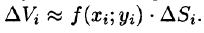 Тогда получаем:
Тогда получаем:
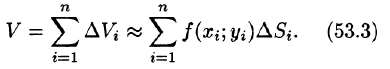
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей»  ,. Естественно принять предел суммы (53.3) при условии, что число площадок
,. Естественно принять предел суммы (53.3) при условии, что число площадок  неограниченно увеличивается
неограниченно увеличивается 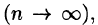 а каждая площадка стягивается в точку
а каждая площадка стягивается в точку 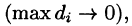 за объем V цилиндрического тела, т. е.
за объем V цилиндрического тела, т. е.
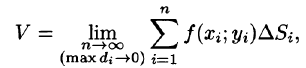
или, согласно равенству (53.2),
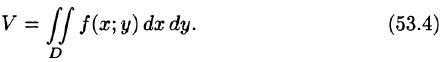
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 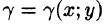 есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей
есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей 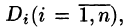 площади которых обозначим через
площади которых обозначим через  . В каждой области
. В каждой области  возьмем произвольную точку
возьмем произвольную точку 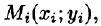 и вычислим плотность в ней:
и вычислим плотность в ней: 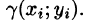
Если области D, достаточно малы, то плотность в каждой точке 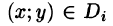 мало отличается от значения
мало отличается от значения 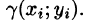 Считая приближенно плотность в каждой точке области
Считая приближенно плотность в каждой точке области  постоянной, равной
постоянной, равной 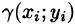 , можно найти ее массу
, можно найти ее массу 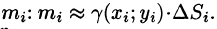 Так как масса m всей пластинки D равна
Так как масса m всей пластинки D равна 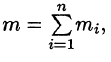 Для ее вычисления имеем приближенное равенство
Для ее вычисления имеем приближенное равенство
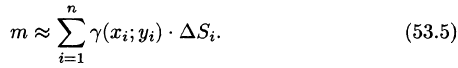
Точное значение массы получим как предел суммы (53.5) при условии 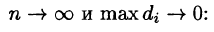
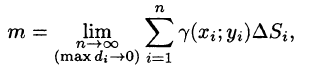
или, согласно равенству (53.2),
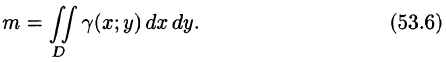
Итак, двойной интеграл от функции 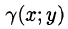 численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию 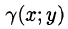 считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
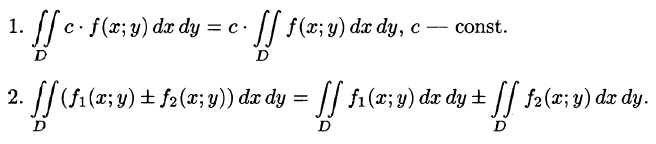
3.Если область D разбить линией на две области 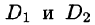 такие, что
такие, что 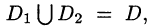 а пересечение
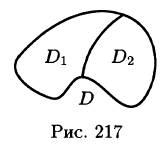
а пересечение 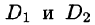 состоит лишь из линии, их разделяющей (см. рис. 217), то
состоит лишь из линии, их разделяющей (см. рис. 217), то
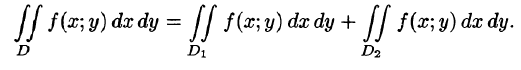
4.Если в области D имеет место неравенство 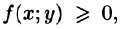 то и
то и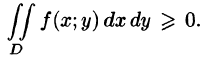 Если в области D функции f(x;y) и
Если в области D функции f(x;y) и 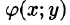 удовлетворяют неравенству
удовлетворяют неравенству 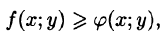 то и
то и
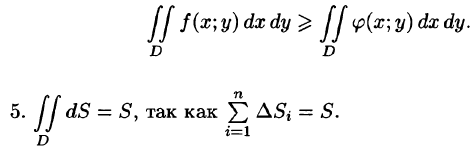
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 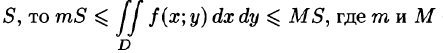 — соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
— соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка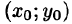 , что
, что 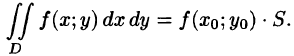 Величину
Величину
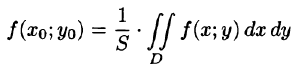
называют средним значением функции f(x; у) в области D.
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 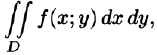 где функция
где функция 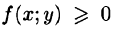 непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
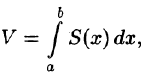
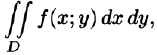
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми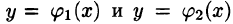 , причем функции
, причем функции 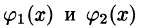 непрерывны и таковы, что
непрерывны и таковы, что 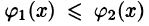 для всех
для всех 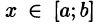 (см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
(см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси 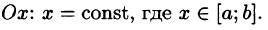
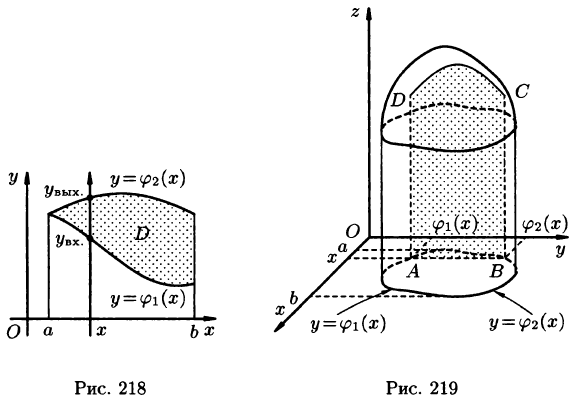
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
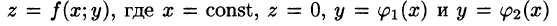
(см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
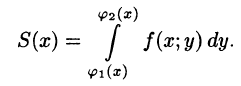
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
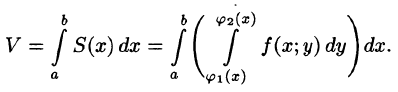
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 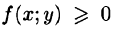 по области D. Следовательно,
по области D. Следовательно,
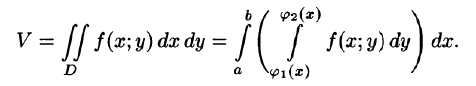
Это равенство обычно записывается в виде
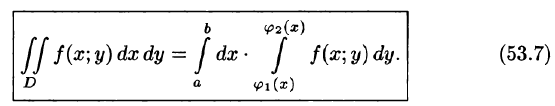
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 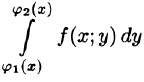 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 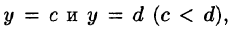 кривыми
кривыми
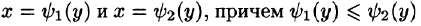
для всех 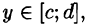 т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
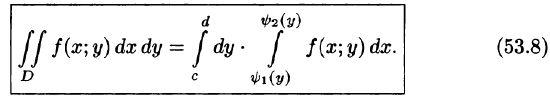
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
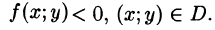
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 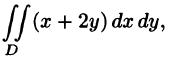 где область D ограничена линиями у
где область D ограничена линиями у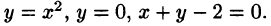
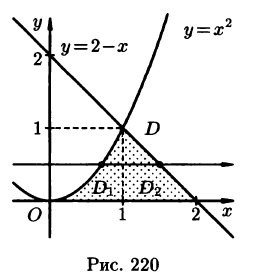
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
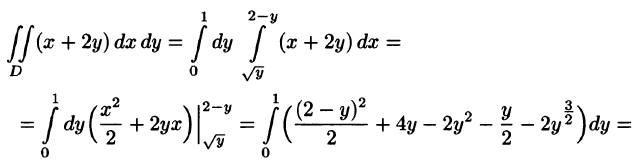
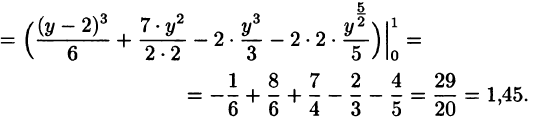
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 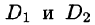 . Получаем:
. Получаем:
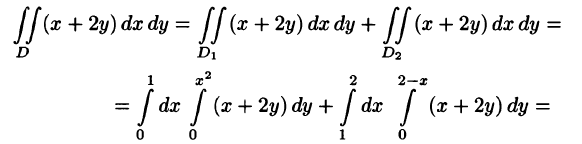
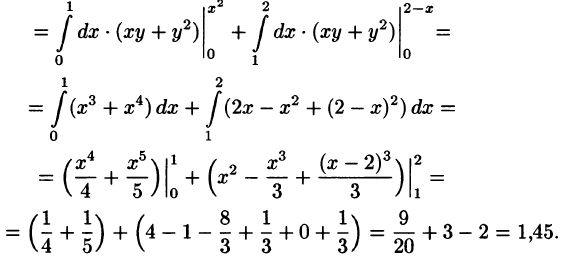
Ответ, разумеется, один и тот же.
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
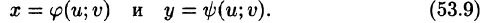
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
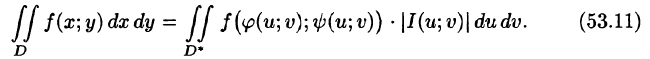
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами 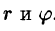
В качестве инь возьмем полярные координаты 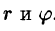 Они связаны с декартовыми координатами формулами
Они связаны с декартовыми координатами формулами 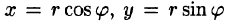 (см. п. 9.1).
(см. п. 9.1).
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
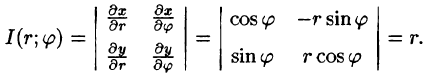
Формула замены переменных (53.11) принимает вид:
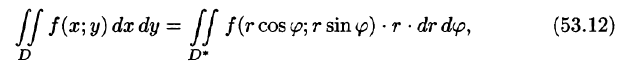
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
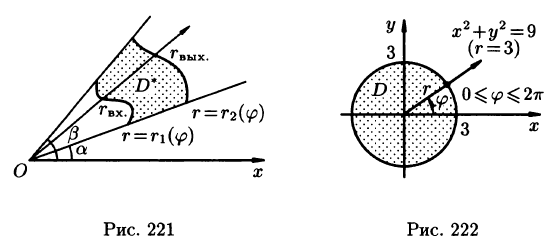
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами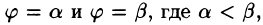 и кривыми
и кривыми 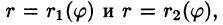 где
где 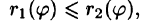 т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
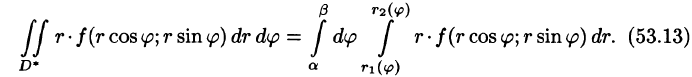
Внутренний интеграл берется при постоянном 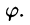
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
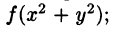 область D есть круг, кольцо или часть таковых.
область D есть круг, кольцо или часть таковых. - На практике переход к полярным координатам осуществляется путем замены
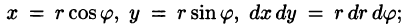 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 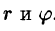 (исследуя закон изменения
(исследуя закон изменения 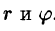 точки
точки 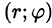 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 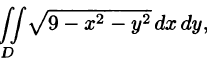 где область D — круг
где область D — круг 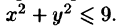
Решение: Применив формулу (53.12), перейдем к полярным координатам:
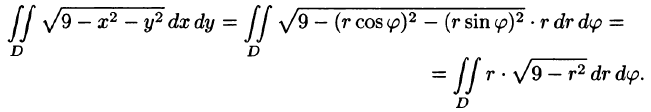
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 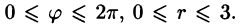 Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
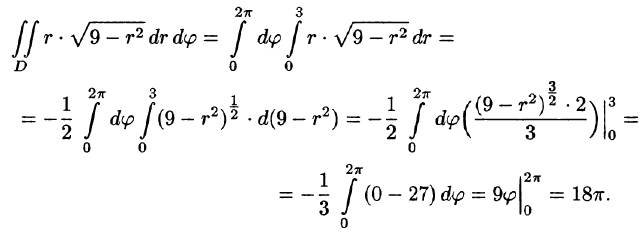
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
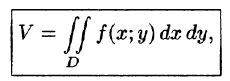
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
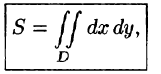
или, в полярных координатах,
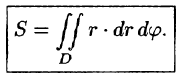
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 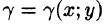 находится по формуле
находится по формуле
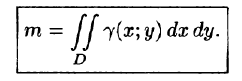
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
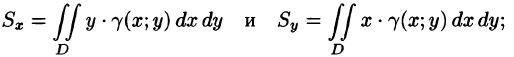
а координаты центра масс фигуры по формулам
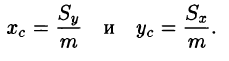
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 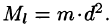 Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
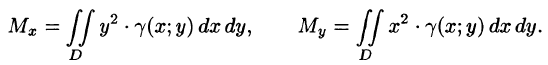
Момент инерции фигуры относительно начала координат — по формуле 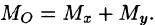
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
Найти объем тела, ограниченного поверхностями
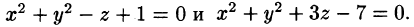
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
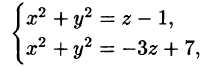
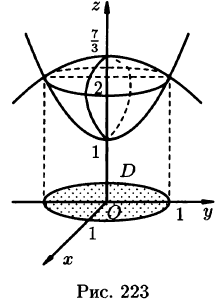
находим уравнение линии их пересечения:
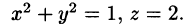
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 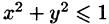 ) и ограниченных сверху соответственно поверхностями
) и ограниченных сверху соответственно поверхностями 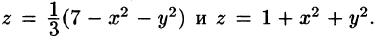 Используя формулу (53.4), имеем
Используя формулу (53.4), имеем
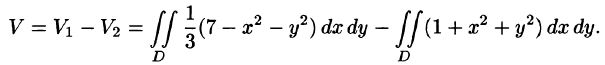
Переходя к полярным координатам, находим:
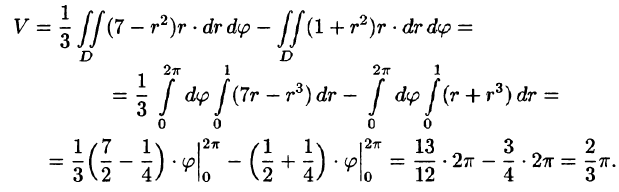
Пример:
Найти массу, статические моменты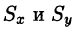 и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом
и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 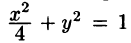 и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
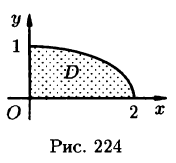
Решение: По формуле (53.6) находим массу пластинки. По условию, 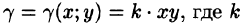 — коэффициент пропорциональности.
— коэффициент пропорциональности.
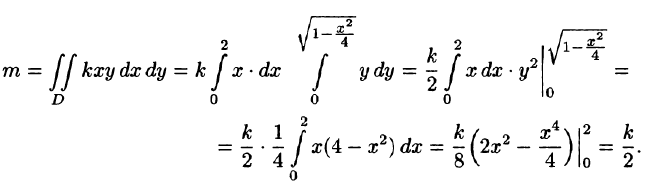
Находим статические моменты пластинки:
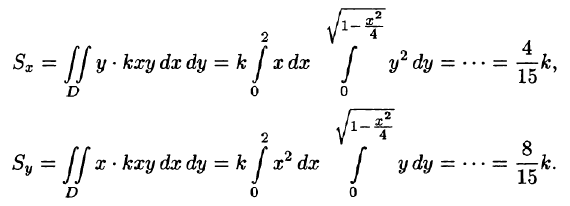
Находим координаты центра тяжести пластинки, используя формулы
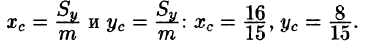
Двойной интеграл












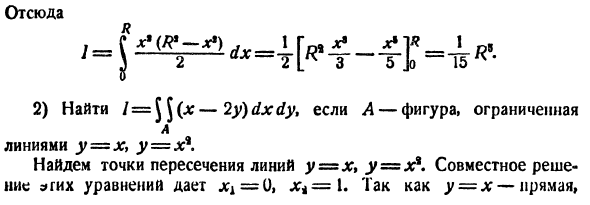


















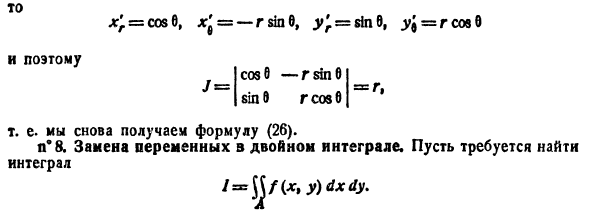

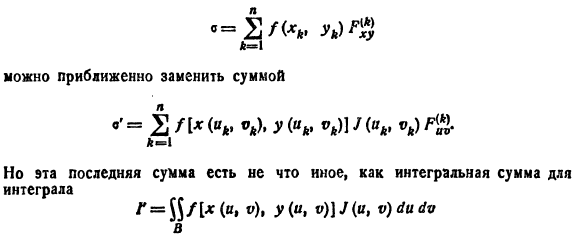



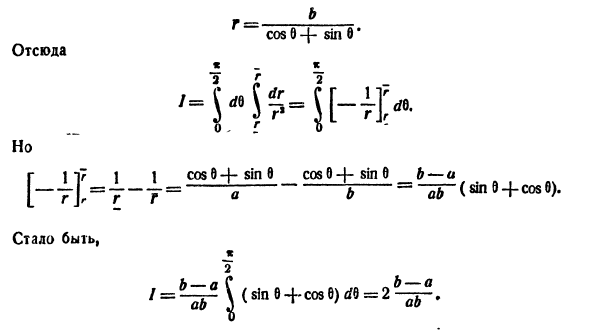

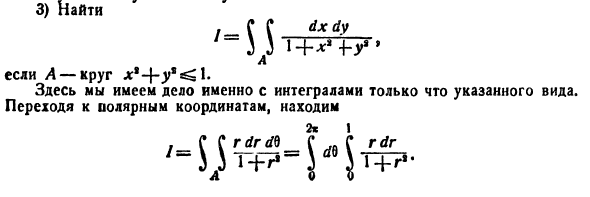





Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Если ![]() –
–
ограниченная область плоскости ![]() ,
,
то ее площадь ![]() вычисляется
вычисляется
по формуле
![]() т.е. если в области
т.е. если в области ![]() подинтегральная
подинтегральная
функция ![]() ,
,
то значение интеграла (1) численно равно
площади области ![]() .
.
Пусть ![]() -неотрицательная,
-неотрицательная,
непрерывная функция в замкнутой
области ![]() .
.
Если ![]() –
–
тело, ограниченное сверху поверхностью ![]() ,
,
снизу – областью ![]() ,
,
а сбоку – соответствующей цилиндрической
поверхностью с образующей параллельной
оси OZ и направляющей, совпадающей с
границей области ![]() ,
,
то объем этого тела равен![]() .
.
Пусть ![]() –
–
тело, ограниченное сверху поверхностью ![]() ,
,
снизу – поверхностью ![]() ,
,
причем проекцией обеих поверхностей
на плоскость ![]() служит
служит
область ![]() ,
,
в которой функции ![]() и
и ![]() непрерывны
непрерывны
(и ![]() ),
),
то объем этого тела равен![]() .
.
12) Вычисление площади поверхности с помощью двойного интеграла
Площадь
поверхности Ω , заданной уравнением z
= f ( x , y )
вычисляется
по формуле: ![]() где
где
D − ортогональная проекция области Ω
на плоскость OXY.
13) Криволинейный интеграл 1-го рода.
Криволинейным
интегралом первого типа от
функции f(х, у, z) по кривой L называется
предел интегральной суммы 2 при ![]() и
и
max ![]() :
:
![]()
![]()
![]() 2
2
14) Вычисление криволинейного интеграла 1-го рода с помощью определённого.
Предположим,
что кривая L
определяется параметрическими
уравнениями x=фи(t),
y=Ψ(t),
(аьфа<=t<=бета).
Кривая L
называется гладкой , если функции φ(t)
и Ψ(t)
обладают непрерывными производными
φ’(t)
и Ψ’(t)
на отрезке [a,b].
Кривую L
будем называть кусочно-гладкой, если
она непрерывна и распадается на конечное
число не имеющих общих внутренних точек
кусков, каждый из которых представляет
собой гладкую кривую. Если кривая L
является кусочно-гладкой кривой, а
функция f(x,y)
непрерывна на кривой L,
то существует криволинейный интеграл
первого рода и справедливо равенство:
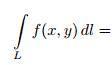
 *
*![]()
15)Криволинейный интеграл 2-го рода. Физический смысл. Свойства.
Сумму
![]()

![]()
записывают
в виде
![]()
![]()
![]()
и
называют
криволинейным
интегралом
II
рода
(по
координатам).
Свойства:
1.
Если меняется направление обхода кривой
АВ, то интеграл меняет знак.
![]()
![]()
2.Если
кривая АВ состоит из частей, то полный
интеграл равен сумме интегралов каждой
части.
![]()
![]()
![]()
Физический
смысл криволинейного интеграла 2-го
рода
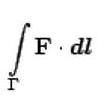 –
–
работа силы ![]() при
при
перемещении вдоль пути ![]() .
.
Интеграл по замкнутой кривой обозначают
через
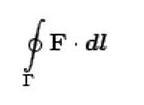 .
.
16) Вычисление криволинейного интеграла 2-го рода с помощью определённого. Связь между интегралами 1-го и 2-го рода.
Вычисление
Пусть ![]() —
—
гладкая, спрямляемая кривая, заданная
параметрически (как в определении).
Пусть функция![]() определена
определена
и интегрируема вдоль кривой![]() в
в
смысле криволинейного интеграла второго
рода. Тогда
![]()
![]() ,
,
![]() ,
,![]()
![]() .
.![]()
Если
обозначить за ![]() единичный
единичный
вектор касательной к кривой![]() ,
,
то нетрудно показать, что
![]()
![]()
![]()
Связь
между криволинейными интегралами 1-го
и 2-го рода.
Криволинейные
интегралы I и II рода связаны
отношением:
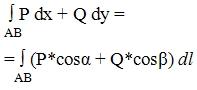
“Альфа”
и “бета” – углы между касательной
кривой с осями Ox и Oy.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
