- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе – это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь – это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
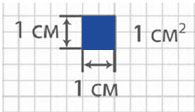
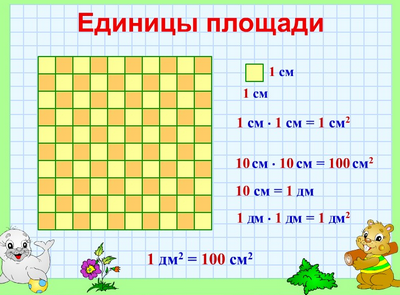
Квадратный сантиметр
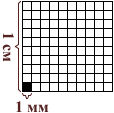
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
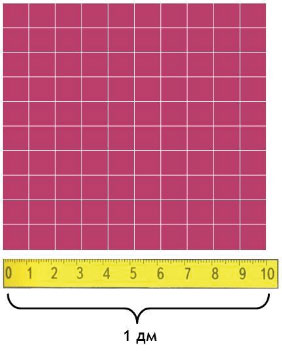
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
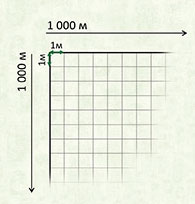
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
Квадратный миллиметр
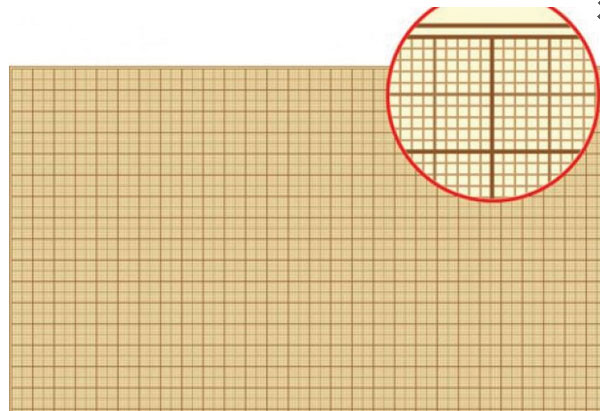
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
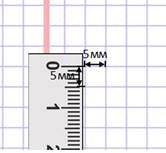
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар – это площадь квадрата со стороной 10 м.
Слово “ар” при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар – это площадь квадрата со стороной 100 м.
Слово “гектар” при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 47. Урок 18,
Петерсон, Учебник, часть 2
Страница 61. Урок 24,
Петерсон, Учебник, часть 2
Страница 68. Урок 27,
Петерсон, Учебник, часть 2
Страница 81. Урок 33,
Петерсон, Учебник, часть 2
Страница 85. Урок 35,
Петерсон, Учебник, часть 2
Страница 91. Урок 38,
Петерсон, Учебник, часть 2
Страница 100. Урок 41,
Петерсон, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 3
Страница 49. Урок 17,
Петерсон, Учебник, часть 3
Страница 56. Урок 20,
Петерсон, Учебник, часть 3
3 класс
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 79,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 111,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 88. Урок 38,
Петерсон, Учебник, часть 2
Страница 75. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 55,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 29. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Рабочая тетрадь, часть 2
- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №8
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 2
- Урок 42. Комментирование решения уравнения
ГДЗ учебник по математике 2 класс Петерсон. Урок 42. Комментирование решения уравнения. Номер №8
- Предыдущее
- Следующее
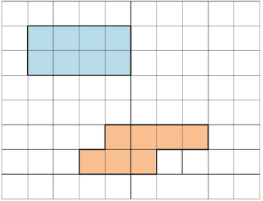
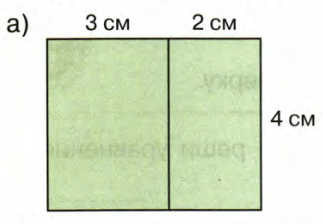
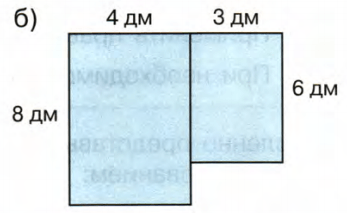
Найди площадь фигур:
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 42. Комментирование решения уравнения. Номер №8
Решение а
1) 3 + 2 = 5 (см) − длина фигуры;
2) 5 * 4 = 20
(
с
м
2
)
− площадь фигуры.
Ответ: 20
с
м
2
Решение б
1) 4 * 8 = 32
(
д
м
2
)
− площадь большого прямоугольника;
2) 3 * 6 = 18
(
д
м
2
)
− площадь маленького прямоугольника;
3) 32 + 18 = 50
(
д
м
2
)
− площадь фигуры.
Ответ: 50
д
м
2
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Ход урока.
1.
Оргмомент. Положительный настрой.
Что такое? Что
случилось?
Почему звенит звонок?
Дети:
Мы готовы. Стол в
порядке.
Начинается урок.
2.
Устный счет.
Отдохнуть
вы все успели?
А
теперь вперед – за дело.
Математика
нас ждет,
Начинаем
устный счет.
|
|
|
1) – 2) Минутка |
– Угадайте, о какой цифре пойдет речь.
Смотрит мама с нетерпеньем
На страницы дневника.
Ждет заветную оценку
У сынка-озорника.
Но опять одни четверки.
Нет красавицы…
– Сегодня на минутке чистописания мы будем
работать с цифрой 5.
– Запишите все двузначные числа, в которых 5
десятков.
51 52 53 54 55 56 57 58 59
3) Арифметический диктант.
1. 4 увеличить на 20 24
2. 4 увеличить на 5. 20
3. 40 уменьшить на 20 20
4. 40 разделить на 5. 8
5. Умножте5 на 5 25
6. При умножении этого числа на само себя получается 36. О каком числе
идет речь? 6
Проверка.
2) Задание на карточках «Расшифруй слово».
30 + 25 = П 4 · 6 = Ь 10 : 5 =
О 100 – 1 = Д
40 – 11 = Щ 5 · 3 = Л 15 : 3 =
А
– Какое слово вы расшифровали? (Площадь) (Слайд №1)
3.
Изучение нового материала.
1. Подготовка.
– Что вы представляете себе, когда слышите слово площадь?
– Названия каких площадей вы знаете?
– Как выглядит Красная площадь? (Слайд №2)
– Красная площадь – это центральная площадь
Москвы .Возникновение Красной площади относится к концу 15 века, когда по
приказу царя Ивана III были снесены деревянные постройки вокруг Кремля,
угрожавшие царской резиденции постоянными пожарами. На их месте была
организована площадь для мелкой торговли. Первоначально она так и называлась
– Торговая. Красной площадь стали называть только в 17 веке.
Так выглядела Красная площадь до Великой Отечественной войны (1926
год). (Слайд №3)
– Кто знает, откуда произошло слово «площадь?»
– Слово «площадь» произошло от слова «плоский» (Слайд №4)
– Давайте прочитаем первое значение этого слова.
– А если площадь маленькая, как ее называют? (Площадка)
– Прочитаем второе значение. Площадка бывает детская, строительная,
спортивная и т.д.
2. Изучение нового материала.
– Сегодня мы с вами познакомимся с еще одним значением слова
«площадь». Это слово часто будет звучать сегодня на уроке.
– Кто уже догадался, какова тема нашего урока? (Слайд №5)
– Как вы думаете, что мы сегодня должны узнать, чему научиться?
– А для того, чтобы лучше понять новую тему, нам понадобятся старые
знания.
Блиц-опрос. Слайд №6 – 7.
– У какого четырёхугольника противоположные стороны
равны?
– У какого четырёхугольника все углы прямые?
– Какая фигура имеет 4 стороны?
– Какая фигура имеет 3 стороны?
– Про какую фигуру можно сказать, что у нее нет
углов?
– У какого четырехугольника все стороны равны?
-У какой фигуры нет начала и конца?
Сторона квадрата равна 3
см. Чему равен периметр квадрата?
– Молодцы.
Физминутка
Слайд №8.
– Чем похожи эти фигуры? (Квадраты)
– Чем отличаются? (Цветом,
размером)
– Какая фигура занимает меньше
места на плоскости? (Красный квадрат)
– Как вы это установили? («На глаз»)
– Подумайте, как еще можно узнать, какая фигура
занимает меньше места на плоскости?
–
Меньше места на
плоскости занимает красный квадрат, так как он полностью помещается внутри
синего квадрата. В математике говорят так: «Площадь красного квадрата
меньше, чем площадь синего квадрата, или площадь синего квадрата больше, чем
площадь красного квадрата».
– Какими же способами можно
измерить площади фигур?
– Давайте выясним, какое же еще
значение имеет слово «площадь»? Для этого обратимся к толковому словарю
Владимира Даля (Слайд №9 – читает 1 ученик, затем хором читаем
определение)
3.
Практическая работа.
– У вас на партах лежат
разноцветные геометрические фигуры. Положите перед собой синий круг, желтый
треугольник, красный квадрат и зеленый треугольник.
– Фигуры с одинаковой площадью
положите справа от себя, а фигуру с наименьшей площадью – слева от себя.
– А теперь проверяем (Слайд №10)
– У кого получилось так же,
поднимите руки.
– Какими способами вы пользовались?
– А теперь скажите, что больше –
площадь стены или классной доски, площадь тетрадного листа или площадь
учебника? Что можно сказать о площади окон в нашем классе? (Одинаковая
площадь)
4. Проблемная ситуация.
Слайд №11.
– Золушка и Незнайка – соседи. У
Золушки – участок розового цвета, у Незнайки – синего. Ваша задача –
определить, у кого из них участок больше.
– У вас на партах есть еще 2 фигуры
– это модели участков наших героев. Попробуйте сравнить площади этих фигур.
– Можно ли определить «на глаз» –
площадь какой фигуры больше?
– Давайте попробуем наложить одну
фигуру на другую. Получается?
– С какой проблемой мы столкнулись?
– Для этого существует еще один
способ. Нужна единица измерения. Пусть это будет вот такой квадрат.
– Разобьем наши участки на
одинаковые квадраты.
Как измерить площадь?
Нет задачи проще!
Поглядите-ка сюда –
Встали мерки в три ряда.
Будто бы солдатики –
Ровные квадратики!
Чтобы площадь нам узнать,
Надо их пересчитать!
Сколько квадратов вмещает участок
Золушки? (9) Участок Незнайки? (9)
– К какому выводу мы пришли? (Площади
этих фигур одинаковые)
– Посмотрите, что получается.
Площадь фигуры – это величина,
значит ее можно измерить.
Одинаковые квадраты – это единицы
измерения (мерки).
Полученные числа – меры величины.
Их можно сравнивать.
4.
Закрепление.
С.29 № 6 –
коллективно.Один ученик у доски, остальные работают в тетрадях.
5.
Итог урока.
–
С каким новым понятием мы сегодня познакомились?
–
Как можно разными способами измерить площади фигур?
–
Что вам особенно понравилось на уроке?
6.
Рефлексия.
–
У вас на партах лежат маленькие листочки. Кто считает, что он сегодня очень
хорошо потрудился, пусть нарисует красный круг.
–
Кто считает, что он сегодня на уроке хорошо работал, но где-то что-то не
получилось – пусть нарисует зеленый квадрат.
–
Если вы думаете, что на уроке вы работали плохо – нарисуйте синий
треугольник.
–
А теперь покажите мне свои фигуры.
(Слайд
№12)
–
Вы сегодня все были… молодцы!
Как найти площадь четырехугольника для 2 класса?
Что такое площадь для 2 класса?
Площадь – свойство фигуры, занимать место на плоскости. Площадь – это внутренняя часть фигуры. . – Наложить мы не сможем эти фигуры, но можем разделить на квадраты и узнать, сколько квадратов занимают фигуры. Площадь фигуры можно измерять и другими мерками.
Что такое площадь 2 класс математика?
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой. Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится.
Как найти площадь треугольника если известны две стороны?
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
Как объяснить ребенку что такое площадь?
Для начала попроще и поменьше. Предложите ребенку пальцем сосчитать все кубики, которые составляют фигуру. Скажите, что общее их количество называется площадью фигуры. Сколько места занимает фигура в некоторых единицах измерения, так в числовом виде выражается ее площадь.
Как найти периметр и площадь 2 класс?
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.
Как найти площадь Как найти площадь квадрата?
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат. S = a * a = a 2 , где где S — площадь, a — сторона.
Что такое площадь Как найти площадь квадрата?
Теория.Площадь квадрата
- Площадь квадрата равна квадрату длины его стороны. S = a 2
- Площадь квадрата равна половине квадрата длины его диагонали. S = d 2
Как найти площадь прямоугольника в 3 классе?
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину. Площадь прямоугольника вычисляется умножением длины АК на ширину КМ.
Что такое площадь простыми словами?
Площадь – это размер двухмерной фигуры (плоской или неровно-поверхностной, искривленной), что принято называть квадратурой. . Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры.
Что такое площадь 3 класс математика?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. Прямоугольник – это четырёхугольник, у которого все углы прямые.
Что обозначает площадь в математике?
Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма).
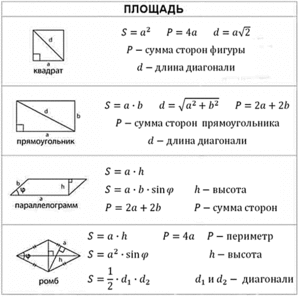
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
Тема урока “Площадь фигуры. Единицы площади”. 2-й класс
Класс: 2
Презентация к уроку
Загрузить презентацию (573 кБ)
Цель: познакомиться с понятием площадь фигуры.
Задачи:
- учить находить площадь фигуры с помощью мерки – квадратного сантиметра. Начать систематизировать представления о способах сравнения и измерения площадей; закреплять навыки счёта в пределах 100;
- развивать внимание, логическое мышление, интеллектуальные и коммуникативные общеучебные умения; организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять ошибки;
- воспитывать интерес к изучению математики.
Оборудование: презентация, модели: квадратные сантиметры, квадратные дециметры, квадратные метры.
| Этапы урока | Деятельность учителя | Деятельность учащихся |
| I. Мотивирование к учебной деятельности. |
1. Организационный момент.
Здравствуй, мой любимый класс,
Очень рада видеть вас!
Ты готов начать урок?
Всё ль на месте?
Всё ль в порядке?
Ручки, книжки и тетрадки?
Приветствуют учителя.
Проверяют свою готовность к уроку.
II. Актуализация знаний.
Устный счёт.
1)Вставьте пропущенные числа.
2) Решите задачу.
В аллее 28 каштанов, а ясеней в 4 раза меньше. Сколько ясеней растёт в аллее?
Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения.
III. Определение темы урока.
2. Постановка проблемы.
– Как называются данные на доске фигуры?
– Что их объединяет? (Это многоугольники, стороны которых равны 2 см.)
– Как найти периметр каждого многоугольника?
2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см).
2 + 2 + 2 + 2 + 2 = 10 (см).
– Как найти площадь этих фигур?
– Какие трудности у вас возникли?
– Сегодня на уроке мы узнаем, что называют площадью фигуры.
Фиксируют затруднение.
IV. Открытие нового знания.
Какая фигура меньше занимает места на плоскости?
Говорят, что треугольник имеет меньшую площадь, четырёхугольник.
– Площадь какой фигуры больше?
Площадь – свойство фигуры, занимать место на плоскости.
Площадь – это внутренняя часть фигуры.
– Площадь квадрата больше, чем площадь круга?
– Площадь какой фигуры больше красной или жёлтой?
– Сможем ли мы сравнить площади фигур наложением?
– Наложить мы не сможем эти фигуры, но можем разделить на квадраты и узнать, сколько квадратов занимают фигуры.
Площадь фигуры можно измерять и другими мерками.
Сравните жёлтый и красный прямоугольники по количеству квадратов.
– Сколько квадратов в первом прямоугольнике, во втором?
– Почему так получилось?
Чтобы этого не было вводятся специальные размеры квадратов. Длина стороны квадрата 1 см.
Работают с презентацией.
Треугольник занимает меньше места.
Площадь четырёхугольника больше, чем площадь треугольника. Это видно на глаз.
Площадь квадрата больше, чем площадь круга. Проверим способом наложения.
Площадь двух кругов одинаковая.
Сравнивают прямоугольники по количеству квадратов.
Т.к. фигуры разбиты на квадраты разных размеров.
V. Первичное закрепление.
Работа в парах.
– Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь.
Фигуры у всех разные, но что у них одинаковое?
-Образуйте фигуры, площадь которой 5 кв. см. (4 кв.см) Назовите площадь.
Чтение правила по учебнику стр. 27.
(Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.)
– Сформулируйте определение квадратного метра.
– Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади.
Их обозначают так: см 2 , дм 2 , м 2 .
– Рассмотрите вырезанные из бумаги квадраты площадью 1 дм 2 , 1 см 2 и 1 м 2 .
– Сравните попарно площади этих квадратов.
– В квадрате площадью 1 дм 2 может уместиться ровно 100 квадратов площадью 1 см 2 , а в квадрате площадью 1 м 2 – ровно 100 квадратов площадью 1 дм 2 .
Работают в парах. У учащихся модели 1кв. см.
У наших фигур одинаковые площади.
Читают определение квадратного дециметра, формулируют определение квадратного сантиметра, метра.
Сравнивают попарно площади этих квадратов, накладывая меньший квадрат на больший.
Физминутка.
Определите площади фигур на экране.
1) Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см 2 .
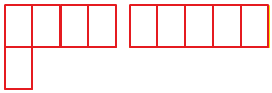
2) Прямоугольник на рисунке состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см.
1) Фигура состоит из 8 квадратов со стороной 1 см каждый. Значит, площадь всей фигуры равна 8 см 2 .
2) Весь прямоугольник состоит из 5 * 3 = 15 таких квадратов, и его площадь равна 15 см 2 .
VI. Самостоятель ная работа. Работа в группах.
Дополни высказывание.
- 1 группа. Квадратной единицей называют не квадрат, а его (площадь).
- 2 группа. Квадратным сантиметром называют площадь квадрата с длиной стороны (1 см).
- 3 группа. Квадратным дециметром называют площадь квадрата с длиной стороны (1 дм).
- 4 группа. Квадратным метром называют площадь квадрата с длиной стороны (1 м).
Работают в группах. Дополняют высказывание.
VIII. Систематизация и повторение.
Задание № 3 (с. 28).
Работа в печатной тетради № 2.
Напиши площадь данных фигур.
Читают величины, записанные единицами площади.
Устанавливают взаимосвязь между изученными единицами площади: 1 дм 2 = 100см 2 .
Записывают площадь фигур.
VII. Итог урока.
Выбери правильное утверждение:
1. Единицы измерения площади:
а) см
б) кв.см
в) кг
2. Площадь – это .
а) сумма длин всех сторон
б) внутренняя часть фигуры
в) всё, что находится вокруг фигуры Что нового узнали на уроке?
– Назовите единицы измерения площади фигуры.
Пригодится ли вам в жизни умение находить площадь фигур?
– Где и зачем?
Выбирают правильное утверждение.
Рефлексия деятельности.
Покажите своё настроение в конце урока смайликом.
– Что не получилось? Почему?
Литература.
- В.Н. Рудницкая. Математика: Учебник для 2 класса, рабочая тетрадь № 2 для 2 класса.- М.: Вентана-Граф.
- Костицын В.Н. Моделирование на уроках геометрии: теория и методические рекомендации. – М.: Владос, 2000.
- Развитие критического мышления на уроке. Пособие для учителей общеобразовательных учреждений . С. И. Заир-Бек, И. В. Муштавинская. — 2-е изд., М. : Просвещение, 2011.
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
http://urok.1sept.ru/articles/640759
[/spoiler]


















 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.