Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
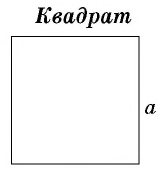
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
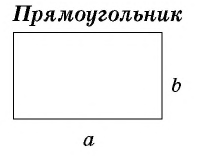
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
A combined figure is a geometrical shape that is the combination of many simple geometrical shapes.
To find the area of combined figures we will follow the steps:
Step I: First we divide the combined figure into its simple geometrical shapes.
Step II: Then calculate the area of these simple geometrical shapes separately,
Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.
Solved Examples on Area of combined figures:
1. Find the area of the shaded region of the adjoining figure. (Use π = (frac{22}{7}))
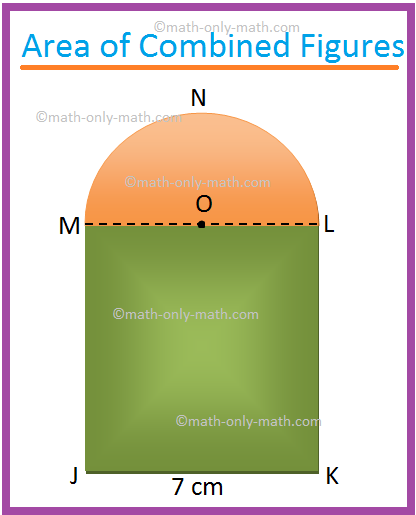
JKLM is a square of side 7 cm. O is the centre of the
semicircle MNL.
Solution:
Step I: First we divide the combined figure into
its simple geometrical shapes.
The given combined shape is combination of a
square and a semicircle.
Step II: Then calculate the area of
these simple geometrical shapes separately.
Area of the square JKLM = 72 cm2
=
49 cm2
Area of the semicircle LNM = (frac{1}{2}) π ∙ ((frac{7}{2})^{2}) cm2 , [Since,
diameter LM = 7 cm]
=
(frac{1}{2}) ∙ (frac{22}{7}) ∙ (frac{49}{4}) cm2
=
(frac{77}{4}) cm2
=
19.25 cm2
Step III: Finally, add these areas up to get
the total area of the combined figure.
Therefore, the required area = 49 cm2 + 19.25 cm2
=
68.25 cm2.
2. In the adjoining figure, PQRS is a square of side 14 cm
and O is the centre of the circle touching all sides of the square.
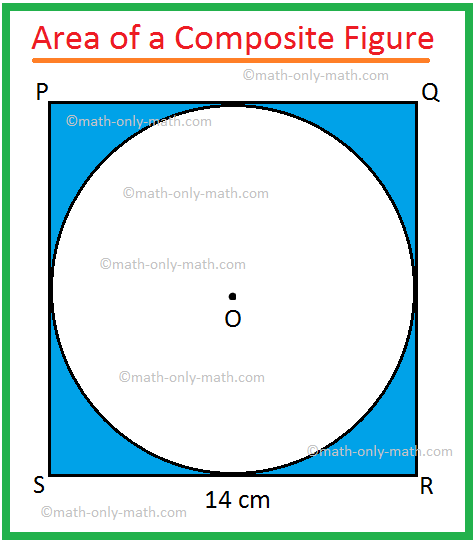
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and a circle.
Step II: Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 142 cm2
= 196 cm2
Area of the circle with centre O = π ∙ 72 cm2, [Since, diameter SR = 14 cm]
= (frac{22}{7}) ∙ 49 cm2
= 22 × 7 cm2
= 154 cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.
Therefore, the required area = 196 cm2 – 154 cm2
= 42 cm2
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S.
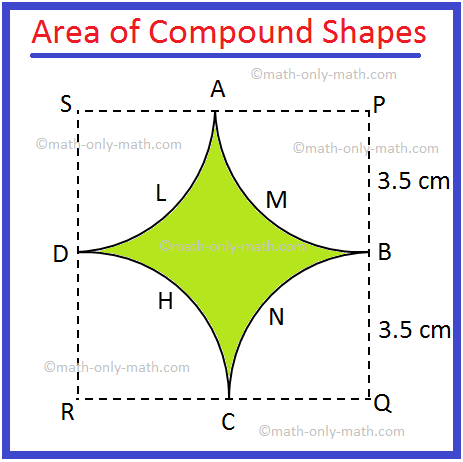
Find the area of the shaded region.
Solution:
Step I: First we divide the combined figure into its simple geometrical shapes.
The given combined shape is combination of a square and four quadrants.
Step II:Then calculate the area of these simple geometrical shapes separately.
Area of the square PQRS = 72 cm2, [Since, side of the square = 7 cm]
= 49 cm2
Area of the quadrant APB = (frac{1}{4}) π ∙ r2 cm2
= (frac{1}{4}) ∙ (frac{22}{7}) ∙ ((frac{7}{2})^{2}) cm2, [Since, side of the square = 7 cm and radius of the quadrant = (frac{7}{2}) cm]
= (frac{77}{8}) cm2
There are four quadrants and they have the same area.
So, total area of the four quadrants = 4 × (frac{77}{8}) cm2
= (frac{77}{2}) cm2
= (frac{77}{2}) cm2
Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.
Therefore, the required area = 49 cm2 – (frac{77}{2}) cm2
= (frac{21}{2}) cm2
= 10.5 cm2
10th Grade Math
From Areas of Combined Figures to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
План урока:
Площадь прямоугольного треугольника
Площадь произвольного треугольника
Площадь параллелограмма
Площадь ромба
Площадь трапеции
Площадь прямоугольного треугольника
Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?
Прямоугольный треугольник можно достроить до прямоугольника:

Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что

Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.
Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:

Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.
Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:

Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:
x = 10
Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.
Ответ: 10; 20.
Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:

Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:

Подсчитаем площадь каждой из трех фигур по отдельности:

Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:

Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):

Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:

Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S1, S2 и S3:

Площадь произвольного треугольника
Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:

В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:

Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:

В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:

Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):

На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:

Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:

Итак, можно сформулировать следующее правило:

Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.
Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.

Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:

Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.
Решение.
Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что

Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:

Получили одно и то же значение, то есть площади треуг-ков равны.
В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.
Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:

Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:

Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:

Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:

Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:

Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.
Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.
Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.

Решение.
Зная ТН и РЕ, мы сможем найти площадь треуг-ка:

Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ

Величину SРЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:

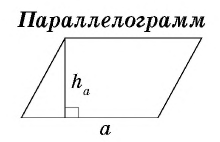
Площадь параллелограмма
Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:

На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.
Опустим в параллелограмме АВСD высоты ВН и СК:

В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).
Раз они равны, то одинаковы и их площади:

Но величину S3 можно заменить на S2. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:

Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:

Задание. Найдите площадь параллелограмма, изображенного на рисунке:

Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:

Далее надо просто перемножить эти длины:

Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:

Дальше можно просто посчитать по отдельности S1, S2и S3, после чего сложить их. Попробуйте сделать это самостоятельно.
Задание. Площадь параллелограмма равна 162 см2, а одна из его высот вдвое короче основания, к которому она проведена. Найдите эту высоту и основание.
Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:

Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.
Ответ: 9 и 18.
Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.
Решение. Опустим на сторону длиной 14 см высоту:

Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:

Площадь ромба
Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.
Построим ромб и проведем в нем диагонали:

Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:

Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, SAOB:

В результате мы доказали следующее утверждение:

Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.
Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:

Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.
Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:

Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30
Ответ: 10 и 30 см.
Площадь трапеции
Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.
В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:

Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:

Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:

В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:

Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.

Решение. Это простая задача на использование формулы площади трапеции:

Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):

Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:

Считаем площадь:

Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?
Решение. Выполним построение:

Найдем острый угол трапеции. Так как CD||АВ, то

Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:

ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:

Из равенства треуг-ков следует, что

Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.
Давайте вспомним, как найти площадь прямоугольника. Чтобы найти
площадь прямоугольника, надо длину умножить на ширину.
Вот формула для нахождения площади прямоугольника:
S = a · b
В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.
Выполним задание, в котором надо найти площадь
прямоугольника со сторонами 5 см и 3 см.
Решение. Итак, чтобы найти площадь
прямоугольника, надо его длину умножить на ширину.
Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в
квадратных единицах. В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
3 · 5 =
15 (см2)
Ответ: площадь прямоугольника равна 15 см2.
Теперь давайте найдём площадь квадрата со стороной 4 см.
Решение. У этого квадрата каждая
сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата
равна 16 квадратным сантиметрам.
4 · 4 =
16 (см2)
Ответ: площадь квадрата равна 16 см2.
Ну а сейчас перейдём к решению задач, в которых нам надо будет
найти площадь сложных фигур.
Найдите площадь фигуры, изображённой на рисунке.
Эта фигура не является ни прямоугольником, ни квадратом. Но мы
можем разделить эту фигуру на два прямоугольника, например, вот таким образом.
А площади прямоугольников мы легко можем найти с помощью
известной формулы.
Напомним, что противоположные стороны прямоугольника равны.
Итак, стороны первого прямоугольника равны 5 см и 4 см.
5 · 4 =
20 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
Ширина этого прямоугольника равна 2 см.
7 – 4 = 3 (см) – длина второго прямоугольника
3 · 2 = 6
(см2) – площадь второго прямоугольника
Мы нашли площади прямоугольников, из которых состоит сложная
фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.
20 + 6 = 26
(см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Площадь этой сложной фигуры найти другим способом. Можно разделить
её на два прямоугольника вот таким образом.
Найдём площадь первого прямоугольника.
Одна его сторона равна 4 см.
5 – 2 = 3 (см) – длина стороны первого прямоугольника
4 · 3 =
12 (см2) – площадь первого прямоугольника
Теперь найдём площадь второго прямоугольника.
7 · 2 =
14 (см2) – площадь второго прямоугольника
12 + 14 =
26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Решим следующую задачу.
Найдём площадь ещё одной фигуры, изображённой на рисунке.
Чтобы найти площадь этой фигуры, тоже разделим её на простые
фигуры. Сделаем это вот таким образом.
Получилось 3 прямоугольника.
Найдём площадь первого прямоугольника.
7 · 2 =
14 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
7 – 4 = 3 (см) – длина одной стороны второго прямоугольника
8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника
Получается, что это квадрат, так как длина всех его сторон равна 3
см.
3 · 3 = 9
(см2) – площадь квадрата
И найдём площадь последнего прямоугольника.
Его ширина равна 3 см. Длина равна 7 см.
3 · 7 =
21 (см2) – площадь третьего прямоугольника
Таким образом, мы нашли площади всех трёх фигур, на которые
разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму
площадей трёх фигур.
14 + 9 + 21 =
44 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 44 см2
Отметим, что площадь этой фигуры можно было бы найти, разделив её
на простые фигуры и вот таким образом:
И решим ещё одну задачу.
Найдите площадь незаштрихованной фигуры.
На рисунке изображён прямоугольник со сторонами 9 см и 5 см.
Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см
и 3 см. Давайте найдём площадь каждого из них.
9 · 5 =
45 (см2) – площадь большего прямоугольника
5 · 3 =
15 (см2) – площадь меньшего прямоугольника
А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.
45 – 15 =
30 (см2) – площадь незаштрихованной фигуры
Ответ: площадь незаштрихованной фигуры равна 30 см2.
Решение задач на вычисление площадей многоугольников чаще всего сводится к поиску величин отдельных элементов рассматриваемых фигур и дальнейшему применению соответствующих формул площадей.
Во многих задачах наряду с сугубо геометрическими приемами решения (дополнительные построения, применение равенства фигур и т. п.) используются и методы алгебры (составление уравнений или систем уравнений на основе метрических соотношений между элементами фигуры).
В ходе решения особое внимание следует уделить тому, однозначно ли данные задачи определяют взаимное расположение элементов фигуры.
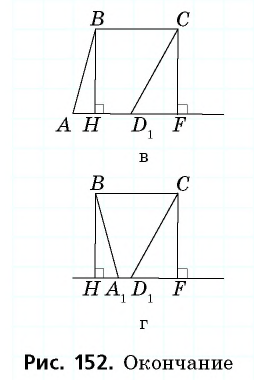
Пример:
Найдите площадь трапеции, в которой одно из оснований равно 24 см, высота 12 см, а боковые стороны — 13 см и 20 см.
Решение:
Пусть 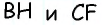
1) Для трапеции 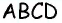 (рис. 152, а): из треугольника
(рис. 152, а): из треугольника 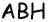 по теореме Пифагора имеем
по теореме Пифагора имеем 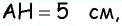 аналогично из треугольника
аналогично из треугольника  имеем
имеем 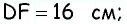 тогда
тогда 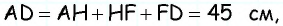
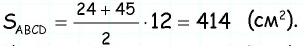
2) Для трапеции  (рис. 152, б): из треугольника
(рис. 152, б): из треугольника 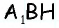 по теореме Пифагора имеем
по теореме Пифагора имеем 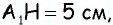 аналогично из треугольника
аналогично из треугольника 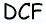 имеем
имеем 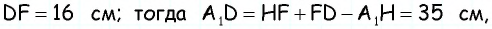
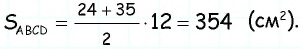
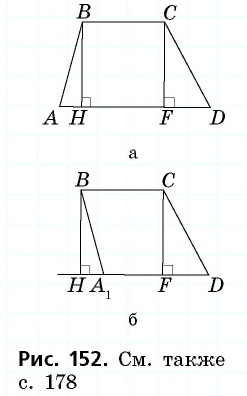
3) Для трапеции  (рис. 152, в): из треугольника
(рис. 152, в): из треугольника  по теореме Пифагора имеем
по теореме Пифагора имеем 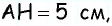 аналогично из треугольника
аналогично из треугольника 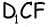 имеем
имеем 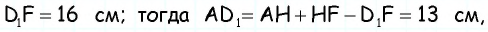
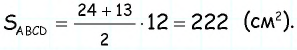
4) Для трапеции 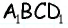 (рис. 152, г): из треугольника
(рис. 152, г): из треугольника 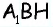 по теореме Пифагора имеем
по теореме Пифагора имеем 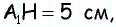 аналогично из треугольника
аналогично из треугольника 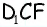 имеем
имеем 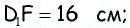 тогда
тогда 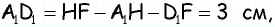 т.е. точки
т.е. точки 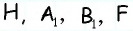 расположены на прямой в указанном порядке.
расположены на прямой в указанном порядке.
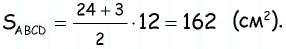
Ответ: 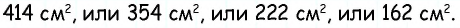
Рассмотренная задача наглядно демонстрирует одну из причин, по которым в процессе решения геометрической задачи может возникать многовариантность. Но даже если такая ситуация не возникает, взаимное расположение элементов фигур нуждается в обосновании.
Пример:
Основания трапеции равны 10 см и 35 см, а боковые стороны — 15 см и 20 см. Найдите площадь трапеции.
Прежде всего заметим, что решение данной задачи фактически сводится к нахождению высоты трапеции. Итак, пусть дана трапеция 
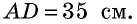
Естественно было бы провести, как в предыдущей задаче, высоты 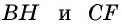 (рис. 153) и составить уравнение на основании теоремы Пифагора, примененной к треугольникам
(рис. 153) и составить уравнение на основании теоремы Пифагора, примененной к треугольникам 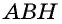 и
и 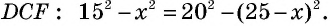
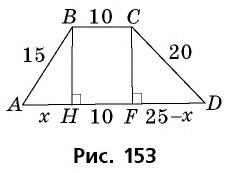
Такое решение позволит получить правильный ответ, но не будет полным, ведь принадлежность точек  отрезку
отрезку  нужно обосновать. Попробуем избежать необходимости такого обоснования, применив для решения другое дополнительное построение.
нужно обосновать. Попробуем избежать необходимости такого обоснования, применив для решения другое дополнительное построение.
Решение:
Проведем через вершину  прямую
прямую 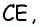 параллельную
параллельную  (рис. 154).
(рис. 154).
Поскольку по построению  — параллелограмм, то
— параллелограмм, то  следовательно,
следовательно, 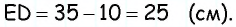 Стороны треугольника
Стороны треугольника 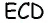 пропорциональны числам 3, 4, 5, следовательно, по теореме, обратной теореме Пифагора, он является прямоугольным с гипотенузой
пропорциональны числам 3, 4, 5, следовательно, по теореме, обратной теореме Пифагора, он является прямоугольным с гипотенузой 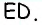
По формуле 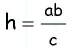 находим высоту этого треугольника, которая одновременно является и высотой трапеции:
находим высоту этого треугольника, которая одновременно является и высотой трапеции: 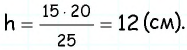 Следовательно,
Следовательно, 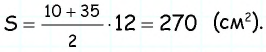
Ответ: 270 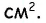
Как видим, этот способ намного более рационален, в частности, с точки зрения вычислений. Рассмотрим еще одну задачу, для решения которой используется дополнительное построение.
Пример:
Диагонали трапеции равны 30 см и 40 см и пересекаются под прямым углом. Найдите площадь трапеции.
Попробуем решить эту задачу чисто геометрическими методами. Основная сложность заключается в том, что данные отрезки не являются сторонами одного треугольника. Попробуем «исправить» эту ситуацию.
Решение:
Пусть дана трапеция  в которой
в которой 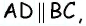
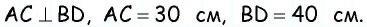 Проведем через вершину
Проведем через вершину 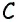 прямую
прямую 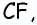 параллельную диагонали
параллельную диагонали 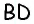 (рис. 155).
(рис. 155).
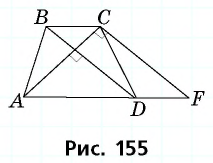
Очевидно, что по построению угол 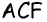 будет прямым, т.е. треугольник
будет прямым, т.е. треугольник 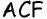 прямоугольный с гипотенузой
прямоугольный с гипотенузой 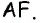 С другой стороны,
С другой стороны, 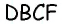 — параллелограмм, тогда
— параллелограмм, тогда 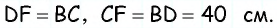
Обратим внимание на то, что треугольники 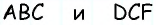 равновеликие, поскольку
равновеликие, поскольку 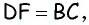 а высоты, проведенные к этим сторонам, являются высотами трапеции. Таким образом,
а высоты, проведенные к этим сторонам, являются высотами трапеции. Таким образом, 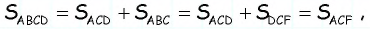 т.е. искомая площадь трапеции равна площади треугольника
т.е. искомая площадь трапеции равна площади треугольника  которая, в свою очередь, равна полупроизведению его катетов:
которая, в свою очередь, равна полупроизведению его катетов:
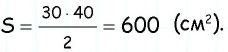
Ответ: 600 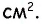
Применение площадей
Теорема (об отношении площадей подобных треугольников)
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство:
Пусть 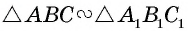 с коэффициентом
с коэффициентом 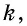 т.е.
т.е. 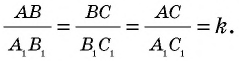 Докажем, что
Докажем, что
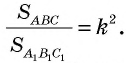
Проведем в данных треугольниках высоты 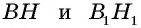 (рис. 161).
(рис. 161).
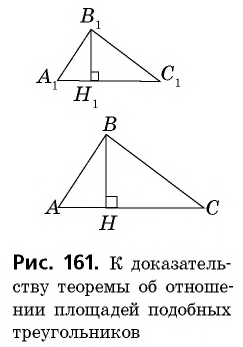
Прямоугольные треугольники 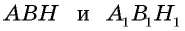 подобны, поскольку
подобны, поскольку 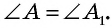 Это означает, что
Это означает, что 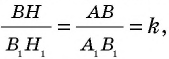 т.е.
т.е. 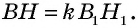 Учитывая, что
Учитывая, что 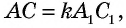 имеем:
имеем:
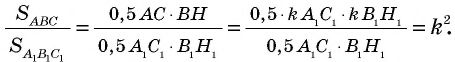
Пример:
Средняя линия отсекает от данного треугольника треугольник с площадью 8 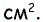 Найдите площадь данного треугольника.
Найдите площадь данного треугольника.
Решение:
Пусть 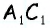 — средняя линия треугольника
— средняя линия треугольника 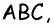 параллельная стороне
параллельная стороне  (рис. 162),
(рис. 162), 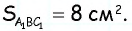
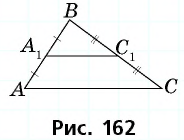
Треугольники 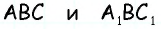 подобны по двум сторонам и углу между ними, причем
подобны по двум сторонам и углу между ними, причем 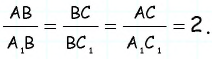 Тогда по доказанной теореме
Тогда по доказанной теореме 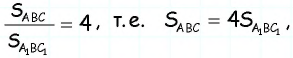 откуда
откуда 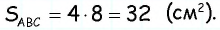
Ответ: 
Метод площадей
Понятия площади и формулы ее вычисления могут применяться даже в тех задачах, в условиях которых площадь не упоминается. Рассмотрим такой пример.
Пример:
Стороны параллелограмма равны 16 см и 12 см. Высота параллелограмма, проведенная к большей стороне, равна 3 см. Найдите высоту, проведенную к меньшей стороне.
Решение:
Пусть дан параллелограмм со сторонами 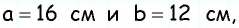 к которым проведены высоты
к которым проведены высоты  длину которой необходимо найти (рис. 163).
длину которой необходимо найти (рис. 163).
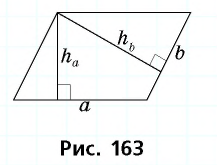
По формуле площади параллелограмма 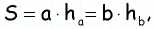 откуда
откуда 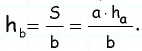
Таким образом, 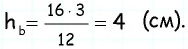
Ответ: 4 см.
При решении этой задачи площадь параллелограмма вычислялась двумя разными способами. Поскольку площадь многоугольника независимо от способа ее вычисления определяется однозначно, то полученные выражения приравнивались, благодаря чему удалось связать известные величины с искомой. Такой метод, основанный на использовании площади как вспомогательной величины, называется методом вспомогательной площади или просто методом площадей.
Заметим, что из формул площади параллелограмма 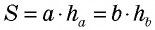 и площади треугольника
и площади треугольника 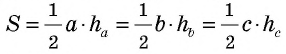 следует важное утверждение: в параллелограмме (треугольнике) большей является высота, проведенная к меньшей стороне, меньшей — высота, проведенная к большей стороне.
следует важное утверждение: в параллелограмме (треугольнике) большей является высота, проведенная к меньшей стороне, меньшей — высота, проведенная к большей стороне.
Метод площадей используется как в задачах на вычисление, так и для доказательства утверждений.
Пример:
Сумма расстояний от точки, взятой внутри равностороннего треугольника, до его сторон не зависит от выбора точки и равна высоте треугольника. Докажите.
Решение:
Пусть точка 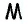 лежит внутри равностороннего треугольника
лежит внутри равностороннего треугольника 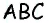 со стороной
со стороной 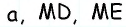 и
и 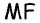 — расстояния от данной точки до сторон треугольника (рис. 164).
— расстояния от данной точки до сторон треугольника (рис. 164).
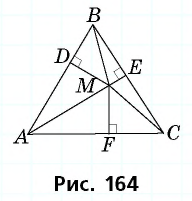
Соединим точку  с вершинами треугольника. Площадь треугольника
с вершинами треугольника. Площадь треугольника  равна сумме площадей треугольников
равна сумме площадей треугольников  и
и 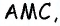 в которых отрезки
в которых отрезки 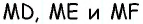 являются высотами. Имеем:
являются высотами. Имеем:
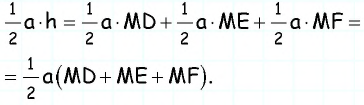
Отсюда 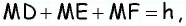 т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки
т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки 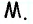
Другие доказательства теоремы Пифагора
Исторически появление и доказательство теоремы Пифагора связаны с вычислением площадей. Поэтому в классической формулировке этой теоремы речь идет не о квадратах сторон прямоугольного треугольника, а о площадях соответствующих фигур:
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, который наглядно воплощает эту формулировку, стал своеобразным символом геометрии и среди гимназистов позапрошлого столетия получил название «пифагоровы штаны».
Шутливый стишок про «пифагоровы штаны» школьники запоминали на всю жизнь.
Докажем теорему Пифагора с помощью площадей.
Доказательство:
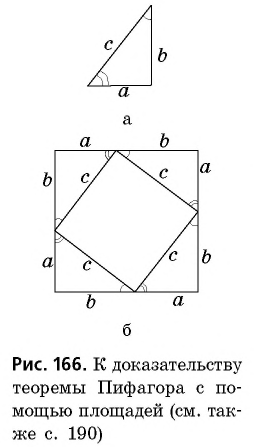
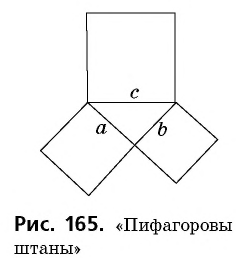
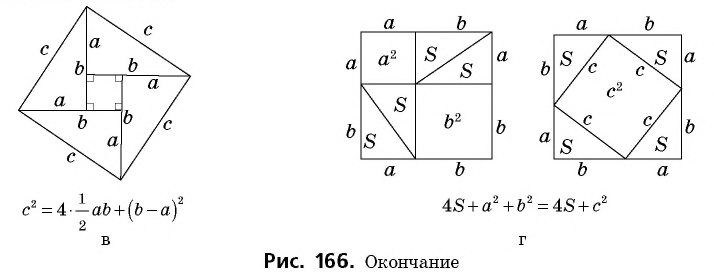
Пусть дан прямоугольный треугольник с катетами 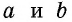 и гипотенузой
и гипотенузой 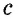 (рис. 166, а). Достроим его до квадрата со стороной
(рис. 166, а). Достроим его до квадрата со стороной 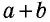 так, как показано на рисунке 166, б. Площадь этого квадрата равна
так, как показано на рисунке 166, б. Площадь этого квадрата равна 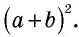 Построенный квадрат состоит из четырех равных прямоугольных треугольников площадью
Построенный квадрат состоит из четырех равных прямоугольных треугольников площадью 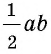 и четырехугольника со сторонами длиной
и четырехугольника со сторонами длиной 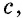 который является квадратом (докажите это самостоятельно). Итак, имеем: ^
который является квадратом (докажите это самостоятельно). Итак, имеем: ^
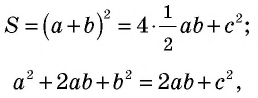
т.е. 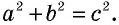
Теорема доказана.
На рисунках 166, в, г показаны другие способы доказательства теоремы Пифагора с помощью площадей. В трактатах индийского математика XII ст. Бхаскари один из них сопровождался только одним словом: «Смотри!». В целом сегодня известно более 150 разных способов доказательства этой знаменитой теоремы. Но каждый из вас может изобрести и свой собственный способ.
Итоги главы 3.
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону
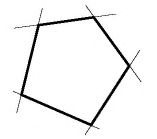
Сумма углов многоугольника
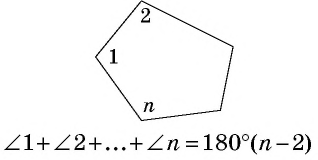
Сумма углов выпуклого 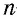 -угольника равна
-угольника равна 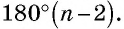
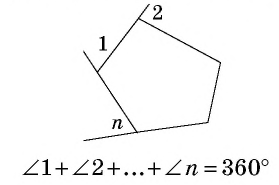
Сумма внешних углов выпуклого 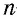 -угольника, взятых по одному при каждой вершине, равна
-угольника, взятых по одному при каждой вершине, равна 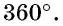
Описанный многоугольник
Многоугольник называется вписанным в окружность, если все его вершины лежат в этой окружности.
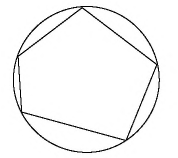
Описанный многоугольник.
Многоугольником называют описанным около окружностей, если все его стороны касаются этой окружности.
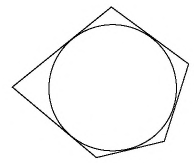
Аксиомы площадей
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади
Две фигуры называются равновеликими, если они имеют равные площади
 где
где  – стороны прямоугольника.
– стороны прямоугольника.
 где
где  — сторона квадрата
— сторона квадрата
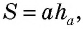 где
где  — сторона параллелограмма,
— сторона параллелограмма,
 — проведенная к ней высота
— проведенная к ней высота
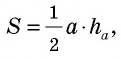 где
где 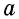 – сторона треугольника,
– сторона треугольника, 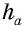 – проведенная к ней высота.
– проведенная к ней высота.
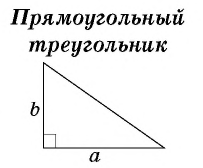
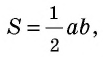
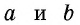 – катеты прямоугольного треугольника.
– катеты прямоугольного треугольника.
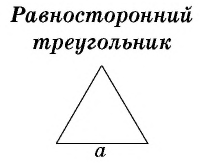
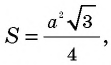 где
где 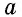 – сторона треугольника.
– сторона треугольника.
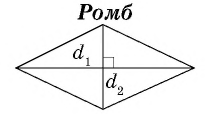
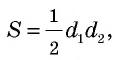 где
где 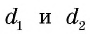 – диагонали ромба.
– диагонали ромба.
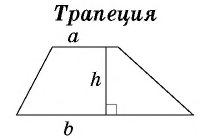
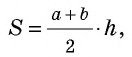 где
где 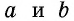 основание трапеции,
основание трапеции, 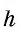 – высота трапеции.
– высота трапеции.
Теорема об отношении площадей подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Историческая справка:
Вычисление площадей многоугольников — первая среди тех практических задач, благодаря которым появилась геометрия как наука. Но не всегда представление об измерении площадей было таким, как сегодня.
Например, древние египтяне при вычислении площади любого треугольника брали половину произведения двух его сторон. Так же пять столетий назад измеряли площадь треугольника и в Древней Руси. Чтобы найти площадь четырехугольника, который не является квадратом, в Вавилоне использовали формулу произведения полусумм его противолежащих сторон.
В Средние века для вычисления площади треугольника со стороной и проведенной к ней высотой, которые выражаются целым числом 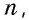 брали сумму членов натурального ряда от 1 до
брали сумму членов натурального ряда от 1 до 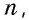 т.е. число
т.е. число 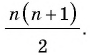
Кстати, в то время знали и правильную формулу площади этого треугольника 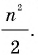 Ее обосновал средневековый математик Герберт, который в X ст. даже занимал какое-то время престол Римского Папы под именем Сильвестра II.
Ее обосновал средневековый математик Герберт, который в X ст. даже занимал какое-то время престол Римского Папы под именем Сильвестра II.
Древние вавилоняне еще четыре тысячи лет назад умели правильно вычислять площадь квадрата, прямоугольника, трапеции. Немало формул площадей и объемов, с которыми вы познакомитесь в старших классах, открыл знаменитый греческий ученый Архимед (ок. 287-212 гг. до н. э.). И это все при том, что в те древние времена не было даже алгебраической символики!
Сегодня, благодаря значительно более широкому применению алгебры в геометрии, мы имеем возможность дать куда более простые и понятные решения многих задач, чем это было возможно в те далекие времена.
- Тела вращения: цилиндр, конус, шар
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Эллипс
- Гипербола
- Парабола
- Многогранник
