Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
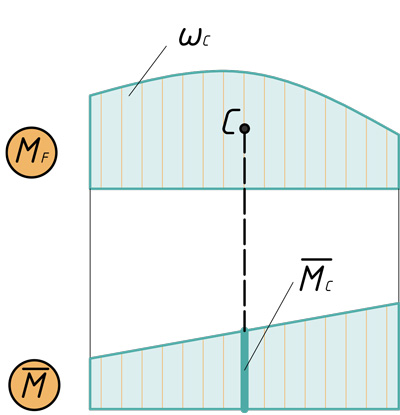
({ V={ M }_{ F } }cdot overline { M } ={ omega }_{ C }cdot { overline { M } }_{ C } )
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
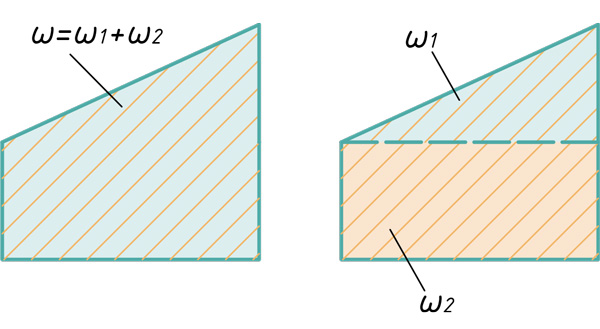
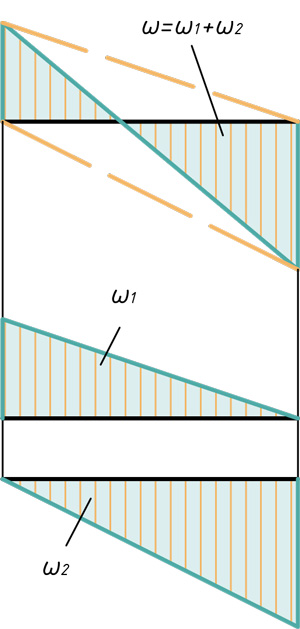
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
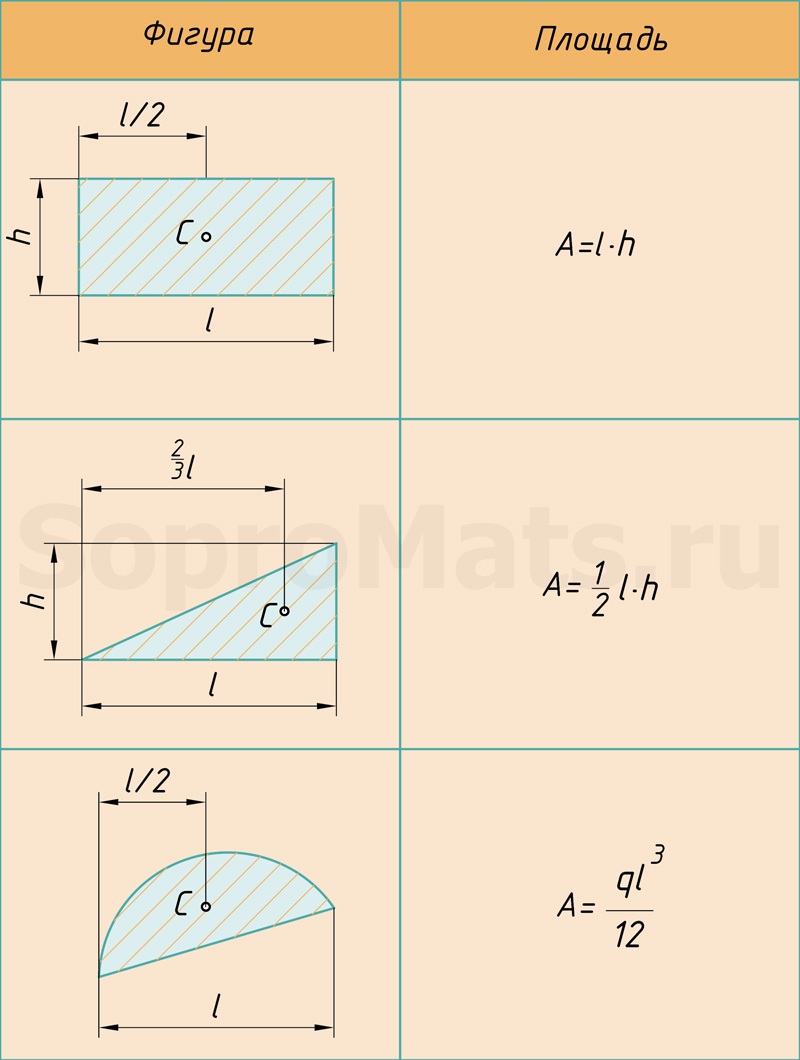
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
Прямоугольник на прямоугольник
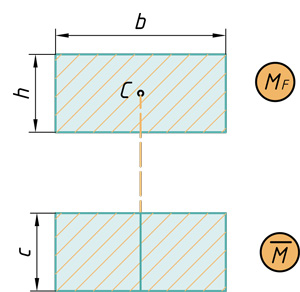
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot c } )
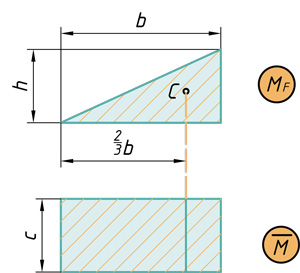
Прямоугольник на треугольник
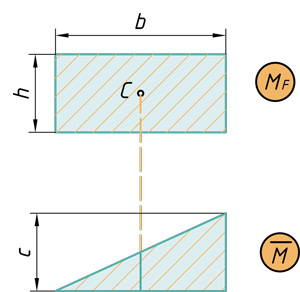
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot frac { 1 }{ 2 } cdot c } )
Треугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { 1 }{ 2 } cdot bcdot hcdot c } )
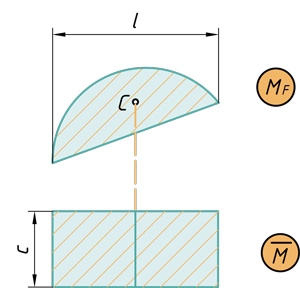
Параболический сегмент на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot c } )
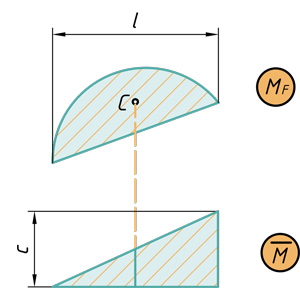
Параболический сегмент на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot c } )
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
Прямоугольник и треугольник
Два треугольника
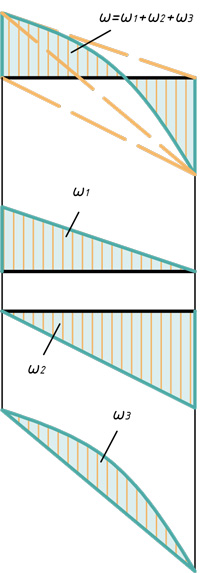
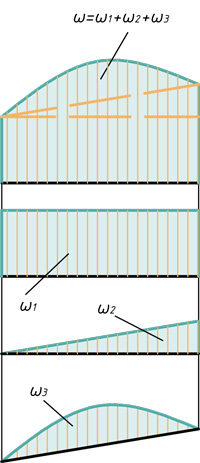
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
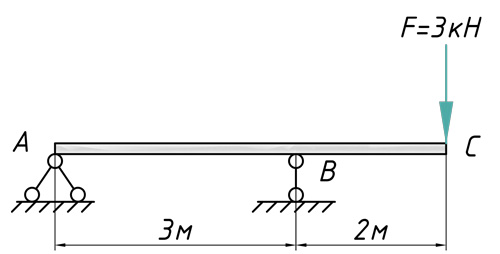
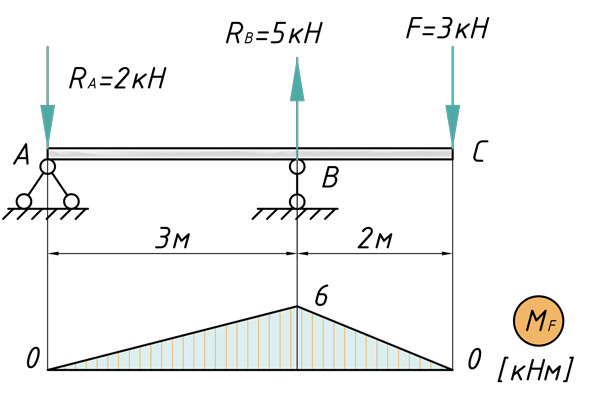
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 2 }{ 3 } cdot 2+frac { 1 }{ 2 } cdot 6cdot 2cdot frac { 2 }{ 3 } cdot 2)=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } ]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
[ { V }_{ C }=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =frac { 20cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =0.289см ]
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
[ { theta }_{ C }=frac { 1 }{ E{ I }_{ x } } (-frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 1 }{ 3 } cdot 1)=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } ]
[ { { theta } }_{ C }=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-frac { 3cdot { 10 }^{ 7 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =-0.0004рад ]
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
Содержание
- Перемножение эпюр по правилу, методу или способу Верещагина
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение простейших эпюр по Верещагину
- Прямоугольник на прямоугольник
- Прямоугольник на треугольник
- Треугольник на прямоугольник
- Параболический сегмент на прямоугольник
- Параболический сегмент на треугольник
- Расслоение эпюр на простые фигуры
- Прямоугольник и треугольник
- Два треугольника
- Два треугольника и параболический сегмент
- Треугольник, прямоугольник и параболический сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- Построение эпюры перемещений
Перемножение эпюр по правилу, методу или способу Верещагина
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
Прямоугольник на прямоугольник
Прямоугольник на треугольник
Треугольник на прямоугольник
Параболический сегмент на прямоугольник
Параболический сегмент на треугольник
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ < V >_< C >=frac < 1 >< E< I >_ < x >> (frac < 1 > < 2 >cdot 6cdot 3cdot frac < 2 > < 3 >cdot 2+frac < 1 > < 2 >cdot 6cdot 2cdot frac < 2 > < 3 >cdot 2)=frac < 20кН< м >^ < 3 >>< E< I >_ < x >> ]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Источник
Построение эпюры перемещений



Построение эпюры нормальных напряжений
Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:
То бишь, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.
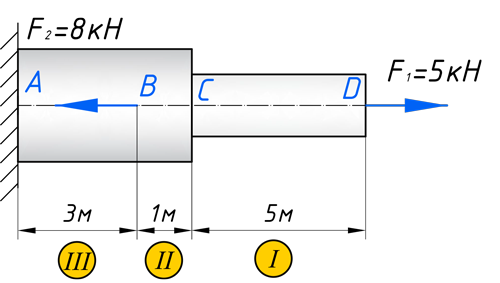
Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:
Зададим брусу на первом участке (I) площадь поперечного сечения A1=2 см 2 , а вторая ступень бруса, допустим, будет иметь площадь A2=4 см 2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию.
Вычисляем напряжения на каждом участке:
По полученным значениям строим эпюру нормальных напряжений:
Построение эпюры перемещений
Самое время перейти к последней эпюре, которая называется эпюрой осевых перемещений поперечных сечений. Для краткости, ее еще называют просто эпюрой перемещений. Для расчета данного графика, пользуются следующей формулой:
Эта формула, является следствием закона Гука. Также ее можно записать как:
Сейчас покажу как ею пользоваться. Все характерные сечения бруса назовем буквами английского алфавита, чтобы потом в решении, было удобно ссылаться на них:
Традиционно расчет перемещений начинают с жестко защемленного торца. Так как сечение в заделке, не имеет возможности перемещаться, то и в решение записываем, что перемещение этого сечения равно нулю:
Далее, для построения эпюры нужно вычислить перемещения в характерных сечениях, которые находятся на границах участков (B, C и D). Этого будет достаточно, так как в пределах участков, эпюра будет меняться по линейному закону. Исключениями могут быть участки, на которых действует распределенная нагрузка, но это тема отдельной статьи.
Приступаем к расчету перемещения сечения B. По формуле, оно будет равно площади эпюры σ, на третьем участке, деленной на модуль упругости — E. При этом, обязательно, учитываем знак эпюры:
Для других сечений, перемещения будут вычисляться аналогичным образом:
ВАЖНО! Вы, наверное, заметили, что для каждого последующего сечения, в расчетах учитывается перемещение предыдущего. Это обязательно необходимо делать.
По полученным значениям, откладываем эпюру перемещений
Вот так, достаточно просто можно построить эпюры для бруса, работающего на растяжение (сжатие).
Эпюры построения смотри ниже.
Решить задачу(домашняя работа)
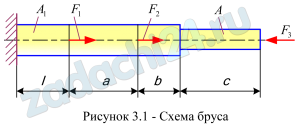
Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений, а также максимальное удлинение.
Принять А=200 мм², А1=400мм 2 ,l=2м, а=4м,в=3м,с=2м,Е=2 ·10 5 МПа.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Прямо сейчас студенты читают про:
ВЫПИСКА, ХРАНЕНИЕ И ПРИМЕНЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ План: 1. Выписка и получение лекарственных средств в ЛПУ. 2. Характеристика лекарственных средств. 3. Требования к хранению.
Соотношение понятий «источник права» и «форма права» Понятия «форма права» и «источник права» тесно взаимосвязаны, но не совпадают.
Основные составляющие (компоненты) физической культуры В настоящее время различают следующие типологические составляющие физической культуры.
Основные положения «Русской правды» П.И. Пестеля Годами трудился Павел Пестель над проектом своей конституции. Он был сторонником диктатуры временного верховного правления во время.
ПОДГОТОВКА ПАЦИЕНТА К ОБЩЕМУ АНАЛИЗУ МОЧИ Цель: · обеспечить качественную подготовку к исследованию и своевременное получение результата.
Источник

б) единичная система
M z1 =1.
Подставим эти усилия в интеграл Максвелла-Мора и возьмем его
|
l |
q x |
2 |
1 |
q l |
3 |
. |
|||||
|
− |
ϕA = − |
||||||||||
|
ϕA = ∫ |
2 E |
dx |
6 |
E J z |
|||||||
|
0 |
J z |
Здесь знак «минус» показывает, что найденное перемещение ϕA и единичный момент направлены в разные стороны.
17.6. Способ Верещагина
При исследовании изгиба стержневых систем оказывается удобным для определения перемещений использовать графо-аналитический метод, предложенный А. Н. Верещаги-
ным (1924).
Так как при определении линейных или угловых перемещений единичная нагрузка будет представлять собой либо силу, либо момент, то эпюра внутреннего изгибающего момента для единичной системы всегда будет ограничена прямыми линиями. В этом случае интеграл Мора можно вычислить следующим образом.
Пусть «грузовая» эпюра MP имеет криволинейное очертание, а «единичная» эпюра M1 представляет собой наклонную прямую (с углом наклона α). На «грузовой» эпюре MP на расстоянии x от начала координат выделим элемент шириной dx. Площадь этого элемента, очевидно, равна dA=MP·dx. «Единичный» момент M1, соответствующий координате x, можно найти через тангенс угла α:
M1 = x tg α.
Запишем теперь интеграл Мора и подставим в него найденные соотношения:
|
∫M P M1 dx = ∫dA x tg α=tg α∫x dA . |
(17.9) |
Выражение под знаком последнего интеграла есть ничто иное, как статический момент «грузовой» эпюры относительно оси Oy
Sy = ∫x dA.
С другой стороны, статический момент можно найти как произведение площади на координату центра тяжести «грузовой» эпюры
Sy = xC A .
В этом случае интеграл (17.9) можно переписать так:
∫M P M1 dx = A xC tg α.
Произведение xC tg α представляет собой величину единичного момента в точке с координатой xC:
26

M1C = xC tg α.
Таким образом, выражение для определения перемещения балки при изгибе по методу Верещагина запишем в следующем виде:
|
∆ = ∑ |
A M1C |
, |
(17.10) |
|
n E Jос |
где А – площадь «грузовой» эпюры MP на данном участке; M1C – величина
«единичного» момента под центром тяжести «грузовой» эпюры на данном участке.
Для удобства использования выражения (17.10) запишем формулы для определения площади и координаты центра тяжести для некоторых характерных эпюр:
а) прямоугольник – А=h·l, xC=l/2; б) треугольник – А=h·l/2, xC=l/3;
в) вогнутая парабола – А=h·l/3, xC=l/4;
г) выпуклая парабола – А=2·h·l/3, xC=3·l/8; д) полная парабола – А=2·h·l/3, xC=l/2.
В качестве примера рассмотрим консольную балку длиной l, нагруженную на конце силой F. Определим прогиб свободного края балки.
Проанализируем две системы грузовую, – нагруженную только силой F, и единичную, – нагруженную единичной силой в направлении искомого перемещения.
Построим для каждой из систем эпюру внутреннего изгибающего момента
(MP и M1).
Площадь «грузовой» эпюры найдем как
A=F·l·l/2.
Значение «единичного» момента под центром тяжести «грузовой» эпюры определим из пропорции
M1C = 2 l
Тогда искомое перемещение |
||||||||||
|
A M1 |
F l3 |
F l3 |
||||||||
|
∆ = |
C |
= |
yA = |
. |
||||||
|
E J z |
3 |
E J z |
3 |
|||||||
|
E J z |
Знак «плюс» показывает, что направление перемещения совпадает с направлением единичной силы.
27
Соседние файлы в папке Лекции по сопромату
- #
- #
- #
- #
- #
- #
Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Площадь – эпюр
Cтраница 1
Площадь эпюра е равняется зазору между двумя любыми сечениями стержня.
[1]
Площадь эпюра Е, построенного для стержня, заделанного своими концами, не имеющего зазоров, должна равняться нулю.
[2]
Следовательно, площадь эпюра Qy равняется алгебраической сумме моментов сосредоточенных пар, приложенных к балке с обратным знаком.
[3]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору.
[4]
Так как в сечении С единичного эпюра – излом, площадь эпюра моментов от заданных сил в этом сечении разбиваем на две части.
[5]
Вектор суммарной силы направлен перпендикулярно оси проводника и проходит через центр тяжести площади эпюра.
[7]
Как следует из вывода правила, в том сечении, в котором имеется излом или скачок в единичном эпюре, площадь эпюра моментов от заданных сил должна разбиваться на две части. Подчеркиваем, что пренебрежение этим приведет к совершенно неверному решению задачи.
[8]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору.
[9]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору.
[10]
Эпюры аксиальной Fz и полной Fs сил представлены на рис. 5.21. В качестве положительного направления Fz принято направление от левого торца индуктора к правому. Площадь эпюра Рг не равна нулю, вследствие чего существует суммарная аксиальная сила, стремящаяся сдвинуть обмотку вправо. Эта сила равна сумме аксиальных сил, действующих на заготовки. На характер распределения полной силы влияют также радиальные силы FR. Эти силы максимальны в зоне немагнитной заготовки, где напряженность Яг примерно в два раза выше, чем в зоне магнитной заготовки.
[11]
Знак момента пары совпадает со знаком скачка от нее на эпюре Мг. Таким образом, изгибающий момент в сечении равняется части площади эпюра Qy, сложенной с алгебраической суммой моментов сосредоточенных пар по одну сторону от сечения.
[12]
Страницы:
1