|
В таком виде вопроса , ответа на задание не существует. Представьте треугольник который нарисован на листе бумаги или , треугольник образованный тремя городами на карте. Площадь таких фигур будет отличатся в десятки тысяч раз. Необходимо знать размеры сторон фигуры. В этом случае площадь высчитывается по математической формуле Герона. автор вопроса выбрал этот ответ лучшим Владислав Ч 8 лет назад Нельзя найти площадь треугольника только через периметр. Формула Герона требует знания ещё и каждой из 3-хсторон. Саму формулу см. в ответе Rafail [20.9K] на Ваш вопрос.
Oleg74 8 лет назад Чтобы найти площадь треугольника, если известен только периметр, то такую площадь найти будет очень сложно, если невозможно. Если треугольник равносторонний, то стороны треугольника по известному периметру можно будет найти , если периметр разделить на 3, а если треугольник – не равносторонний, то тогда тупик, так как в нахождении площади треугольника применяется формула Герона, в которой нужно знать длины всех трех сторон. Формула Герона :
Ksyusha26 8 лет назад Это вполне возможно. Только для этого нужно знать три стороны треугольника. Если известны все три стороны (a,b,c), то тогда используем формулу Герона. Сначала только найдем периметр (p). Извлекаем корень квадратный из числа, которое мы получим следующим выражением: p (p-a)(p-b)(p-c). Вот и все Знаете ответ? |
Площадь треугольника

Определение площади треугольника
Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.
Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.
Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.
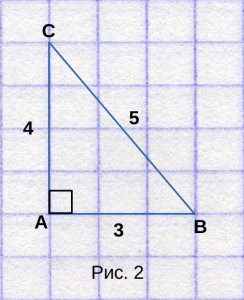
Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.
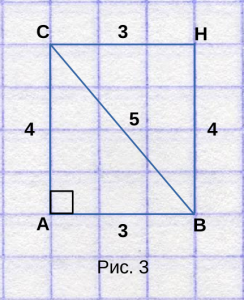
Как видим, весь прямоугольник занимает 12 полных клеток.
Формула площади прямоугольника равна произведению
одной стороны на другую — ( S = ab ) ,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.
Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ( S = frac<1>2 ab ) .
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.
Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.
Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.
Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.
Формулы площади треугольника
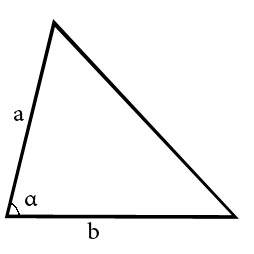
Ⅰ. Через высоту и основание
a — сторона, на которую падает высота,
b — высота.
Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.
Ⅱ. Через все стороны и периметр
p — полупериметр, вычисляется по формуле: ( p = frac <2>) ,
a, b, c — стороны треугольника.
Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.
Эту формулу площади также называют формулой Герона.
Ⅲ. Через две стороны и угол между ними
[ S = frac<1> <2>a cdot b cdot sin β ]
a, b — стороны между которыми расположен угол β,
sin β — синус угла β.
Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.
Ⅳ. Через периметр и радиус вписанной окружности
[ S = r cdot frac
2 ]
r — радиус вписанной окружности,
P — периметр треугольника.
Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.
Ⅴ. Через все стороны и радиус описанной окружности
abc — произведение всех сторон треугольника,
R — радиус описанной окружности.
Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.
Ⅵ. Через сторону и два прилежащих к ней угла
a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.
Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
- Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
- Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
- Поделите все на 4.

Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника

О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://vsvoemdome.ru/obrazovanie/kak-nayti-ploschad-treugolnika
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
[/spoiler]

Формула:
S
=
1
2
ab
·
sin(α)
Где: a, b – катеты, c – гипотенуза.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
4R
Где: a, b, c – стороны разностороннего треугольника, R – радиус описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
abc
2D
Где: a, b, c – стороны разностороннего треугольника, D – диаметр описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Формула:
S
=
a
b
c
4
S
π
Где: a, b, c – стороны разностороннего треугольника, S – площадь описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
π
a
b
c
2P
Где: a, b, c – стороны разностороннего треугольника, P – длина описанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
R
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, R – радиус вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
D
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, D – диаметр вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
SO
π
·
a
+
b
+
c
2
Где: a, b, c – стороны разностороннего треугольника, SO – площадь вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
P
π
·
a
+
b
+
c
4
Где: a, b, c – стороны разностороннего треугольника, P – длина вписанной окружности.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
a2
2
·
sin(α)
·
sin(β)
sin(180-(α+β))
Где: a – сторона, α, β – прилегающие углы.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано

Формула:
S
=
p(p-a)(p-b)(p-c)
p
=
a
+
b
+
c
2
Где: a, b, c – стороны, p – половина периметра.
цифр после запятой
5
-
0
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
обновите расчет!!!
укажите правильное значение!!!
скопировано
Площадь треугольника равна произведению длины вписанной окружности поделенной на пи и четверти периметра треугольника.
Предлагаем простой и удобный калькулятор для расчета площади треугольника в режиме онлайн. Он может оказаться полезным не только для школьников, изучающих базовый курс геометрии, но и для строителей, дизайнеров, архитекторов и многих других специалистов, чья работа так или иначе связана с проектированием и изготовлением различных инженерных конструкций. Вы можете посчитать площадь произвольного треугольника, зная основные размеры, однозначно определяющие его конфигурацию.
Формула расчета площади треугольника по стороне и высоте, проведенной из противолежащей вершины
Зная длину одной из сторон треугольника (основания) и высоту, проведенную к этой стороне, его площадь можно посчитать, перемножив эти величины друг на друга и разделив результат на 2. То есть площадь треугольника — это полупроизведение основания на высоту. Это наиболее известная формула, она применима к любым треугольникам.
Площадь треугольника по трем сторонам, формула Герона
Одна из самых полезных на практике формул, незаслуженно обойденная вниманием во многих популярных источниках. Она позволяет рассчитать площадь треугольника, зная длины трех его сторон. В реальных условиях очень часто трудно провести измерения углов или каких-то линейных размеров конструкций, требующие дополнительных геометрических построений. Что же касается сторон, то они, как правило, или известны, или относительно легко поддаются измерению, поэтому площадь треугольника во многих случаях рассчитывают именно этим способом.
Для определения площади необходимо рассчитать полупериметр треугольника — сумму его сторон, деленную на 2. Далее из него поочередно вычитают длину каждой стороны, а результаты перемножают. Затем полученное значение умножают на полупериметр и из итогового числа извлекают квадратный корень. Это довольно сложный расчет, но с помощью нашего калькулятора вы проделаете его всего за несколько мгновений, введя длины сторон треугольника в предназначенные для этого поля.
Как рассчитать площадь треугольника, если известны две стороны и угол между ними
Эта формула также имеет широкое практическое применение. Например, с ее помощью можно посчитать площадь треугольного фронтона в доме с двускатной крышей. Угол наклона скатов и их длины обычно известны, их достаточно подставить в формулу и получить результат. Наш онлайн-калькулятор сделает это для вас моментально. Алгоритм расчета следующий: площадь треугольника вычисляется как половина произведения длин известных сторон на синус угла, который находится между ними.
Формула площади треугольника по его известной стороне и двум прилежащим углам
Наш калькулятор посчитает площадь треугольника и по этим параметрам. В расчете применяется довольно громоздкая формула, использовать которую при ручном подсчете довольно затруднительно. Поэтому, если вы знаете только эти характеристики треугольника, открывайте нужную вкладку и вводите значения в соответствующие поля калькулятора. Это поможет вам сэкономить время и избежать ошибок, исправлять которые будет сложно и дорого.
Как найти площадь треугольника по его периметру и радиусу вписанной окружности
Если вы знаете длины всех сторон треугольника, лучше использовать приведенную выше формулу Герона. Но если известен только полный периметр (сумма сторон, а не длины каждой из них по отдельности), площадь можно рассчитать как произведение радиуса вписанной окружности на половину периметра. Дизайнеры и проектировщики довольно часто помещают в треугольные фигуры круглые детали, при этом радиусы окружностей обычно бывают известны.
Формула площади произвольного треугольника по трем сторонам и радиусу описанной окружности
Радиус описанной окружности — избыточный параметр. Если длины всех трех сторон треугольника известны, его площадь определяется по формуле Герона. Тем не менее есть возможность несколько упростить расчет: нужно перемножить длины сторон друг на друга и разделить результат на учетверенный радиус описанной окружности. Наш онлайн-калькулятор при необходимости вычисляет площадь фигуры и по этой формуле.
Расчет площади прямоугольного треугольника
Прямоугольный треугольник — это частный случай произвольной треугольной фигуры, один из его углов равен 90°. Для вычисления его площади можно применять любую из приведенных выше формул, при этом многие из них заметно упрощаются. Например, синус прямого угла равен единице, поэтому площадь такого треугольника будет равна полупроизведению прилежащих сторон, которые называются катетами. Радиус описанной окружности для любого прямоугольного треугольника равен половине длины третьей стороны — гипотенузы, так что соответствующая формула также сводится к полупроизведению катетов. Если известен другой параметр — радиус вписанной окружности r, то площадь равна r · (r + c), где c — длина гипотенузы.
Площадь равнобедренного треугольника
В математике треугольник, две стороны которого равны, называется равнобедренным. Третья сторона при этом называется основанием, кроме того, известно, что углы при этом основании равны. Если боковые стороны обозначить буквой b, а находящийся между ними угол — α, то площадь будет равна ½ · b² · sin (α). Это частный случай формулы расчета площади произвольного треугольника по двум известным сторонам и углу между ними. Наш калькулятор использует именно ее.
Формулы для равностороннего треугольника
Если у треугольника все стороны равны, вычисление его площади еще больше упрощается. Достаточно знать длину стороны a или измерить радиус вписанной окружности r. Калькулятор использует одну из следующих формул:
S = √3 / 4 · a²;S = 3√3 · r².
В основе расчета площади треугольника во всех случаях лежит довольно простая математика. Но при этом часто требуется вычислять тригонометрические функции, радикалы и произведения больших чисел. Поэтому самое простое решение — снять все необходимые размеры и воспользоваться нашим калькулятором. Это быстро, точно и бесплатно. Никаких ограничений на количество расчетов и требований по авторизации у нас нет. Если у вас появятся вопросы, вы можете задать их в комментариях.
Онлайн калькулятор площади треугольника. Как узнать площадь треугольника.
При помощи нашего калькулятора вы легко сможете узнать площадь треугольника.
|
|
|
| Вычислить площадъ треугольника через: | |
| Высота треугольника h: | |
| Длина стороны b: |
Существует несколько формул при помощи которых можно вычислить площадь треугольника.
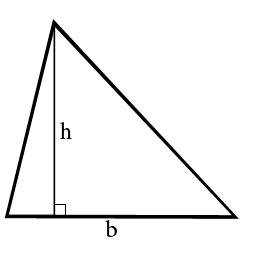
- Мы можем вычислить площадь треугольника зная его высоту и длину основания по следующей формуле:
S=1/2bh
- Так же площадь треугольника можно узнать используя формулу Герона, по которой можно вычислить площадь зная периметр или длину всех сторон треугольника:
S= √p(p-a)(p-b)(p-c)
где p – это полупериметр треугольника
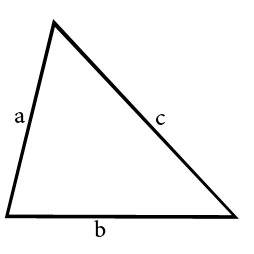
- Еще мы можем узнать площадь треугольника зная длину двух сторон и угол между ними
S=1/2ab sin(α)