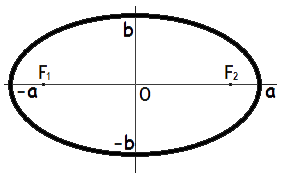Как найти площадь если известна длина формула - Сайт, где вы сможете решить свои вопросы

Как найти площадь прямоугольника?

Анонимный вопрос

18 августа 2019 · 203,8 K

Редактор, автор и переводчик книг по математике · 18 авг 2019 ·

Чтобы найти площадь прямоугольника, надо его длину умножить на ширину

Обрати внимание, что длина и ширина должны быть выражены в одних единицах. Если длина и ширина в сантиметрах, то площадь получится в сантиметрах квадратных; если длина и ширина в километрах, то площадь получится в квадратных километрах. Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.

Очень полезно познакомиться с площадями прямоугольников на практике. Давай я попробую угадать: площадь твоего стола меньше одного квадратного метра. Площадь твоей кровати больше одного квадратного метра, но меньше двух. Площадь твоей комнаты больше 10 квадратных метров и меньше 20 квадратных метров. Мне не видно, и я могла ошибиться. Так что измерь, посчитай и проверь, правильно ли я угадала.

120,8 K

площадь- это длина умноженая на ширину

Комментировать ответ…Комментировать…

7,1 K

Комментировать ответ…Комментировать…

Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
S=a*b
2) через диагонали и угол
S=1/2*d(в квадрате)*sin(α)… Читать далее

7,6 K

Комментировать ответ…Комментировать…

Надо длину умножить на ширину
Пример : 3*2 = 6 квадратных сантиметров ( квадратные сантиметры пишутся так : см и мелкая 2 на верху) так же есть и другие квадратные

5,6 K

Комментировать ответ…Комментировать…

Пример:

У прямоугольника есть 4 стороны. Первые 2 стороны равны друг другу, как и вторые 2 стороны.

Значит, прямоугольник делится на a и b. Представим, что сторона a – 3 сантиметра, а b – 2 сантиметра. Площадь будет буквой S. Чтобы вычислить площадь прямоугольника, нужно сторону a умножить на b. S=a*b. S=3*2. 3*2 это шесть. Площадь обозначается квадратными сантиметрами. S=6 см2

5,1 K

-Как найти площадь Ленина?

-Надо длину Ленина, умножить на ширину Ленина!

Комментировать ответ…Комментировать…

Геймер, програмер, учу английский, чуть-чуть ютубер · 4 мая 2021

У прямоугольника есть длина и ширина.
Длину и ширину надо перемножить.
Ответ надо записывать в квадратной величине (результат и маленькая двойка сверху)
Пример:
Ширина = 3 см
Длина = 7 см
7*3 = 21(см2)
Ответ: 21 см2. Читать далее

2,5 K

Возьмите 2 игральных кубика. Бросьте оба. Первый показывает вам ширину прямоугольника, второй – длину. А площадь -… Читать дальше

Комментировать ответ…Комментировать…

Чтобы найти площадь прямоугольника, нужно умножить две его неравные стороны друг на друга. Также это выражается формулой S = a * b, где S – площадь, a и b – две неравные стороны прямоугольника.
В общей сложности, площадь прямоугольника, можно найти с помощью пяти разных формул.
1. Через две смежные стороны
2. Через любую сторону и периметр
3. Через любую сторону и… Читать далее

9,4 K

Комментировать ответ…Комментировать…

Что бы найти площадь треугольника, нужно воспольщоваться формулой:
S= a•b
Например:
Длина прямоугольника равна 8 см
Ширина прямоугольника равна 4см
Площадь прямоугольника равна 8•4=32 Читать далее

1,5 K

Комментировать ответ…Комментировать…

Чтобы найти площадь прямоугольника надо умножить длину на ширину пример:
a-9 см
b-3 см
s-? см
s=a*b
9*3=27(см)
Ответ:27 сантиметров площадь прямоугольника. Читать далее

2,5 K

Комментировать ответ…Комментировать…

Я работаю сама на себя – плету из бисера украшения и продаю. · 25 окт 2022

Для того чтобы найти площадь прямоугольника надо одну сторону прямоугольника (ширину) умножить на вторую сторону (длина).

Ширина – а

Длина – б

площадь – S

S = а умножить на б

358

Комментировать ответ…Комментировать…

Источник

Содержание

– Как найти площадь прямоугольника если известна высота?
– Как найти площадь прямоугольника если известны стороны?
– Как найти площадь прямоугольника если известна площадь?
– Что нужно сделать чтобы найти площадь?
– Что такое площадь для 3 класса?
– Что такое площадь в математике 4 класс?
– Что значит найти площадь фигуры?

Как найти площадь прямоугольника если известна высота?

Значит для того, чтобы найти площадь прямоугольника нужно его ширину умножить на длину. В виде формулы это можно представить как S = h*b, где S-площадь, h-высота, b-ширина. Или так: площадь прямоугольника = ширина х длину.

Как найти площадь прямоугольника если известны стороны?

Площадь прямоугольника равна произведению его длины на ширину.

Как найти площадь прямоугольника если известна площадь?

Когда известно значение длины и ширины фигуры

Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина. Проверить полученный результат поможет онлайн-калькулятор площади прямоугольника.

Что нужно сделать чтобы найти площадь?

Для вычисления площади прямоугольника нужно умножить его длину на ширину. Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Что такое площадь для 3 класса?

Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. … Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Что такое площадь в математике 4 класс?

Площадь-это свойство фигур занимать место на плоскости. … Квадратный миллиметр- единица измерения площади, равная площади квадрата со стороной 1мм. Основная и дополнительная литература по теме урока: Математика: 4 класс: учебник в 2 ч.

Что значит найти площадь фигуры?

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. … В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Интересные материалы:

Сколько кирпича в1м2?
Сколько кирпичей на поддоне?
Сколько кирпичей в кладке в один кирпич?
Сколько кирпичей в одной упаковке?
Сколько кирпичей в поддоне облицовочного?
Сколько комбикорма съедает курица в день?
Сколько кондиционеров нужно в однокомнатную квартиру?
Сколько корма нужно давать кролику в день?
Сколько корма нужно в день для гусей?
Сколько корма съедает биг 6?

Источник

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

S — искомая площадь прямоугольника;
a и b — соседние стороны.

2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

S — искомая площадь прямоугольника;
a — известная сторона;
D — диаметр описанной окружности.

4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

S — искомая площадь прямоугольника;
a — известная сторона;
R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

S — искомая площадь прямоугольника;
a — известная сторона;
P — периметр прямоугольника (равен сумме всех сторон).

6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

S — искомая площадь прямоугольника;
d — любая диагональ прямоугольника;
α — любой угол между диагоналями прямоугольника.

7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

S — искомая площадь прямоугольника;
R — радиус описанной окружности;
α — любой угол между диагоналями прямоугольника.

Формулы площади геометрических фигур

Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p – a)(p – b)(p – c)
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,

p = a + b + c – полупериметр треугольника.

2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d₁, d₂ – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d₁, d₂ – длины диагоналей.

Формулы площади трапеции

Формула Герона для трапеции

S = a + b √(p-a)(p-b)(p-a-c)(p-a-d)

|a – b|
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,

p = a + b + c + d – полупериметр трапеции.

2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними

Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S – площадь четырехугольника,
d₁, d₂ – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r
Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p – a)(p – b)(p – c)(p – d) – abcd cos²θ

где S – площадь четырехугольника,

a, b, c, d – длины сторон четырехугольника,

p = a + b + c + d2 – полупериметр четырехугольника,

θ = α + β2 – полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность

S = √(p – a)(p – b)(p – c)(p – d)

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

S = π r²
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.

Формулы площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S – Площадь эллипса,

a – длина большей полуоси эллипса,

b – длина меньшей полуоси эллипса.

Источник

Загрузить PDF

Иногда вычисление площади сводится к простому перемножению двух чисел, но зачастую это вычисление более сложное. Прочтите эту статью для краткого обзора по вычислению площади (или площади поверхности) следующих фигур: четырехугольник, квадрат, параллелограмм, трапеция, треугольник, многоугольник, круг, пирамида, цилиндр, кривая линия.

1

Найдите длину двух смежных сторон прямоугольника. Поскольку противоположные стороны прямоугольника равны, нужно найти длины смежных сторон. Обозначьте одну сторону как (b), а другую — как (h).^[1]
2
Перемножьте значения двух смежных сторон, чтобы найти площадь. Обозначим площадь прямоугольника как (k). Тогда: k = b*h.
- Для более детальных инструкций прочтите статью «Как найти площадь четырехугольника».
Реклама

1

Найдите длину стороны квадрата. Поскольку квадраты имеют четыре равные стороны, нужно найти длину всего одной стороны.^[2]
2
Возведите в квадрат длину стороны. Это и есть площадь квадрата.
- Это верно, потому что квадрат — это прямоугольник, у которого все стороны равны. Так как для прямоугольника k = b*h, а в квадрате b=h, для вычисления площади квадрата просто умножаем его сторону на саму себя.
Реклама

1

Выберите одну сторону, на которую будет опущен перпендикуляр. Найдите длину этой стороны.
2
Опустите перпендикуляр (высоту) на выбранную ранее сторону и найдите его длину.^[3]
- Если нужно, продлите сторону, на которую опускается перпендикуляр, до ее пересечения с перпендикуляром.
3

Реклама

1

Найдите длины двух параллельных сторон. Обозначьте их как (а) и (b).
2

Найдите высоту. Опустите перпендикуляр (высоту (h)) к основанию трапеции.^[5]
3

Реклама

1

Найдите длину одной стороны треугольника (b), на которую будет опущен перпендикуляр (высота) и длину высоты (h).
2
Чтобы найти площадь треугольника, подставьте длину соответствующей стороны и длину высоты в формулу: A=0.5b*h
- Для более детальных инструкций прочтите статью «Как найти площадь треугольника».
Реклама

1

Найдите длину стороны и длину апофемы (а) (отрезок, соединяющий центр многоугольника и середину любой из его сторон).
2

Умножьте длину стороны на количество сторон, чтобы найти периметр многоугольника (р).
3

Реклама

1

Найдите радиус окружности (r). Это отрезок, соединяющий центр окружности и любую точку на окружности.
2

Реклама

1

Найдите площадь прямоугольного основания пирамиды с помощью приведенной выше формулы для нахождения площади прямоугольника: k=b*h.
2

Найдите площадь каждой треугольной грани пирамиды с помощью приведенной выше формулы для нахождения площади треугольника: A=0.5b*h.
3

Сложите все полученные площади для вычисления площади поверхности пирамиды.

Реклама

1

Найдите радиус круга в основании цилиндра.
2

Найдите высоту цилиндра.
3

Найдите площадь круга в основании, используя формулу для вычисления площади круга: А=πr^2.
4

Найдите площадь боковой поверхности, умножив высоту цилиндра на периметр основания. Периметр основания равен длине окружности: P = 2πr, поэтому площадь боковой поверхности А= 2πhr.
5
Сложите все полученные площади: две площади круговых оснований и площадь боковой поверхности. Таким образом, площадь поверхности цилиндра: SA = 2πr^2 + 2πhr.
- Для более детальных инструкций прочтите статью «Как найти площадь поверхности цилиндра».
Реклама

Допустим, вы хотите найти площадь фигуры, ограниченной кривой линией (описывается функцией f(x)), осью x и значениями функции при x=а и при x=b (то есть область определения [a,b]). Этот метод потребует знаний интегрального исчисления. Если вы не знаете его, этот метод не имеет для вас никакого смысла.

1

Определите f(x) через x.
2

Возьмите интеграл функции f(x) в интервале [а,b]. По формуле Ньютона-Лейбница: F(x)=∫f(x), ∫abf(x) = F(b) – F(a).
3

Подставьте значения а и b в интегральное выражение. Искомая площадь определяется как ∫abf(x). Поэтому, A=F(b)) – F(a).

Реклама

Об этой статье

Эту страницу просматривали 25 272 раза.

Была ли эта статья полезной?

Источник

p =	a + b + c	– полупериметр треугольника.
2

S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
\|a – b\|

p =	a + b + c + d	– полупериметр трапеции.
2

Как найти площадь прямоугольника?

Как найти площадь прямоугольника если известна высота?

Как найти площадь прямоугольника если известны стороны?

Как найти площадь прямоугольника если известна площадь?

Что нужно сделать чтобы найти площадь?

Что такое площадь для 3 класса?

Что такое площадь в математике 4 класс?

Что значит найти площадь фигуры?

1. Если известны две соседние стороны

2. Если известны любая сторона и диагональ

3. Если известны любая сторона и диаметр описанной окружности

4. Если известны любая сторона и радиус описанной окружности

5. Если известны любая сторона и периметр

6. Если известны диагональ и угол между диагоналями

7. Если известны радиус описанной окружности и угол между диагоналями

Формулы площади геометрических фигур

Формулы площади треугольника

Формула Герона

Формулы площади квадрата

Формула площади прямоугольника

Формулы площади параллелограмма

Формулы площади ромба

Формулы площади трапеции

Формулы площади выпуклого четырехугольника

Формулы площади круга

Формулы площади эллипса

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как составить автобиографию бесплатно

Как найти интернет агент

Как исправить ошибку protect

Добавить комментарий Отменить ответ