Как найти площадь любого треугольника
Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.
- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.
Читайте также 🧠👨🏻🎓✍🏻
- 7 причин полюбить математику
- ТЕСТ: Помните ли вы геометрию?
- 10 хитрых головоломок со спичками для тренировки воображения
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- ТЕСТ: Сможете ли вы решить простые математические примеры?
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона

Формула Герона для нахождения площади треугольника:
– полупериметр треугольника; a,b,c – стороны треугольника.
Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:
a – основание треугольника; h – высота треугольника.
Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:
a,b – стороны треугольника; α – угол между сторонами.
Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
<
a– сторона треугольника; α и β – прилежащие углы.
Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
a, b – катеты треугольника.
Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
a, b – стороны треугольника.
Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:
a – основание равнобедренного треугольника; α – угол между сторонами.
Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
a – сторона равностороннего треугольника.
Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:
h – высота равностороннего треугольника.
Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
r – радиус вписанной окружности равностороннего треугольника.
Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
r – радиус описанной окружности равностороннего треугольника.
Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
a, b, c – стороны треугольника; r – радиус описанной окружности треугольника.
Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
p – полупериметр треугольника;a, b, c – стороны треугольника; r – радиус вписанной окружности треугольника.
Треугольник — это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.
Онлайн-калькулятор площади треугольника
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по основанию и высоте
S=12⋅a⋅hS= frac{1}{2}cdot acdot h,
aa — основание треугольника;
hh — высота треугольника, проведенная к данному основанию a.
Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в формулу для площади и получаем:
S=12⋅10⋅5=25S=frac{1}{2}cdot10cdot 5=25 (см. кв.)
Ответ: 25 (см. кв.)
Формула площади треугольника по длинам всех сторон
S=p⋅(p−a)⋅(p−b)⋅(p−c)S= sqrt{pcdot(p-a)cdot (p-b)cdot (p-c)},
a,b,ca, b, c — длины сторон треугольника;
pp — половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
p=12(a+b+c)p=frac{1}{2}(a+b+c)
Эта формула называется формулой Герона.
Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
Найдем половину периметра pp:
p=12(3+4+5)=12⋅12=6p=frac{1}{2}(3+4+5)=frac{1}{2}cdot 12=6
Тогда, по формуле Герона, площадь треугольника:
S=6⋅(6−3)⋅(6−4)⋅(6−5)=36=6S=sqrt{6cdot(6-3)cdot(6-4)cdot(6-5)}=sqrt{36}=6 (см. кв.)
Ответ: 6 (см. кв.)
Формула площади треугольника по одной стороне и двум углам
S=a22⋅sinβsinγsin(β+γ)S=frac{a^2}{2}cdot frac{sin{beta}sin{gamma}}{sin(beta+gamma)},
aa — длина стороны треугольника;
β,γbeta, gamma — углы, прилежащие к стороне aa.
Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.
Решение
a=10a=10
β=30∘beta=30^{circ}
γ=30∘gamma=30^{circ}
По формуле:
S=1022⋅sin30∘sin30∘sin(30∘+30∘)=50⋅123≈14.4S=frac{10^2}{2}cdot frac{sin{30^{circ}}sin{30^{circ}}}{sin(30^{circ}+30^{circ})}=50cdotfrac{1}{2sqrt{3}}approx14.4 (см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a⋅b⋅c4RS=frac{acdot bcdot c}{4R},
a,b,ca, b, c — стороны треугольника;
RR — радиус описанной окружности вокруг треугольника.
Числа возьмем из второй нашей задачи и добавим к ним радиус RR окружности. Пусть он будет равен 10 (см.).
Решение
a=3a=3
b=4b=4
c=5c=5
R=10R=10
S=3⋅4⋅54⋅10=6040=1.5S=frac{3cdot 4cdot 5}{4cdot 10}=frac{60}{40}=1.5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S=p⋅rS=pcdot r,
pp — половина периметра треугольника:
p=a+b+c2p=frac{a+b+c}{2},
a,b,ca, b, c — стороны треугольника;
rr — радиус вписанной в треугольник окружности.
Пусть радиус вписанной окружности равен 2 (см.). Длины сторон возьмем из предыдущей задачи.
Решение
a=3a=3
b=4b=4
c=5c=5
r=2r=2
p=3+4+52=6p=frac{3+4+5}{2}=6
S=6⋅2=12S=6cdot 2=12 (см. кв.)
Ответ: 12 (см. кв.)
Формула площади треугольника по двум сторонам и углу между ними
S=12⋅b⋅c⋅sin(α)S=frac{1}{2}cdot bcdot ccdotsin(alpha),
b,cb, c — стороны треугольника;
αalpha — угол между сторонами bb и cc.
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b=5b=5
c=6c=6
α=30∘alpha=30^{circ}
S=12⋅5⋅6⋅sin(30∘)=7.5S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!
Тест на тему “Плошадь треугольника”
 Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.
Найти площадь треугольника можно различными способами. Конечно же, в зависимости от данных переменных и подбирается необходимая формула. В основном, для нахождения площади треугольника применяется формула Герона.
Если известны все три стороны треугольника ABC, то формула площади треугольника по трем сторонам легко применится на практике:

где:
- p – полупериметр треугольника,
- a, b, c – длины сторон треугольника.
Периметр – это сумма длин всех сторон треугольника. Соответственно полупериметр – это сумма длин всех сторон разделенная на 2.

![]() Рассмотрим пример расчета площади треугольника по трем сторонам:
Рассмотрим пример расчета площади треугольника по трем сторонам:
Дан треугольник. Стороны a = 3 см., b = 4 см., c = 5 см. Для начала найдем полупериметр
 =6 см.
=6 см.
Далее рассчитаем площадь

Площадь треугольника равна 6 кв. см
Также можно найти площадь треугольника и по другим формулам – через синус и косинус.
| Сторона a= | Сторона b= | Сторона c= | |
| Ответ: Площадь треугольника = 6.000 |

{S = dfrac{1}{2} cdot a cdot h}
Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника – равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.
- Калькулятор площади треугольника
- Площадь треугольника
- через основание и высоту
- через две стороны и угол между ними
- через сторону и два прилежащих угла
- через радиус описанной окружности и 3 стороны
- через радиус вписанной окружности и 3 стороны
- по формуле Герона
- Площадь прямоугольного треугольника
- через катеты
- через гипотенузу и прилежащий угол
- через катет и прилежащий угол
- через радиус вписанной окружности и гипотенузу
- через вписанную окружность
- по формуле Герона
- через катет и гипотенузу
- Площадь равнобедренного треугольника
- через основание и сторону
- через основание, боковую сторону и угол
- через основание и высоту
- через боковые стороны и угол между ними
- через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника
- через сторону
- через высоту
- через радиус описанной окружности
- через радиус вписанной окружности
- Примеры задач
Площадь треугольника
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Площадь треугольника через основание и высоту
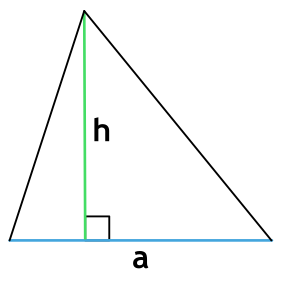
{S = dfrac{1}{2} cdot a cdot h}
a – длина основания
h – высота, проведенная к основанию
Площадь треугольника через две стороны и угол между ними
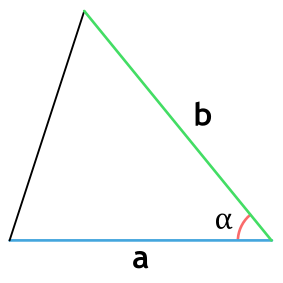
{S = dfrac{1}{2} cdot a cdot b cdot sin(alpha)}
a и b – стороны треугольника
α – угол между сторонами a и b
Площадь треугольника через сторону и два прилежащих угла
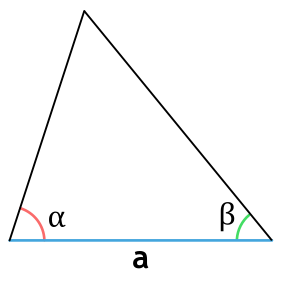
{S = dfrac{a^2}{2} cdot dfrac{sin{(alpha)} cdot sin{(beta)}}{sin{(gamma)}}}
{gamma = 180 – (alpha + beta)}
a – сторона треугольника
α и β – прилежащие к стороне a углы
Площадь треугольника через радиус описанной окружности и 3 стороны
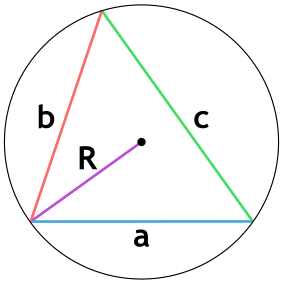
{S = dfrac{a cdot b cdot c}{4 cdot R}}
a, b и c – стороны треугольника
R – радиус описанной окружности
Площадь треугольника через радиус вписанной окружности и 3 стороны
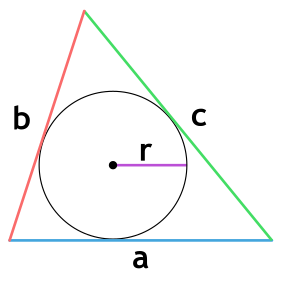
{S = r cdot dfrac{a + b + c}{2}}
a, b и c – стороны треугольника
r – радиус вписанной окружности
Площадь треугольника по формуле Герона
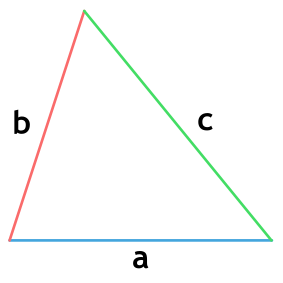
{S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника
Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).
Площадь прямоугольного треугольника через катеты

{S = dfrac{1}{2} cdot a cdot b}
a и b – стороны треугольника
Площадь прямоугольного треугольника через гипотенузу и прилежащий угол
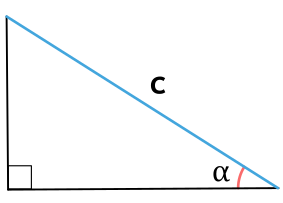
{S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)}}
c – гипотенуза прямоугольного треугольника
α – прилежащий к гипотенузе c угол
Площадь прямоугольного треугольника через катет и прилежащий угол
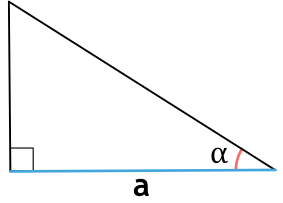
{S = dfrac{1}{2} cdot a^2 cdot tg{(alpha)}}
a – катет прямоугольного треугольника
α – прилежащий к катету a угол
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
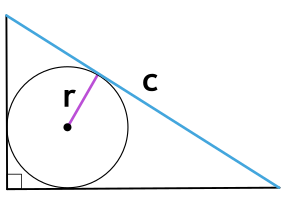
{S = r cdot (r+c)}
r – радиус вписанной окружности
c – гипотенуза прямоугольного треугольника
Площадь прямоугольного треугольника через вписанную окружность

{S = c_1 cdot c_2}
с1 и с2 – отрезки, полученные делением гипотенузы точкой касания окружности
Площадь прямоугольного треугольника по формуле Герона
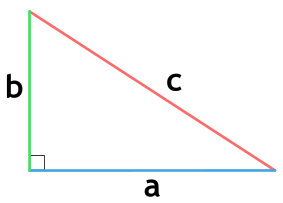
{S = (p-a) cdot (p-b)}
{p= dfrac{a+b+c}{2}}
a, b и c – стороны треугольника
p – полупериметр треугольника
Площадь прямоугольного треугольника через катет и гипотенузу
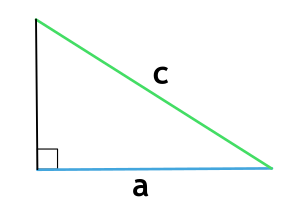
{S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2}}
a – катет прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
Площадь равнобедренного треугольника
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине.
Площадь равнобедренного треугольника через основание и сторону
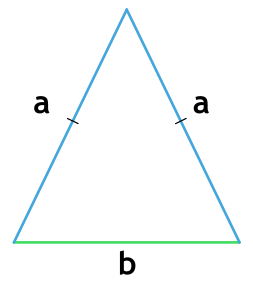
{S = dfrac{b}{4} sqrt{4a^2 – b^2}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
Площадь равнобедренного треугольника через основание, сторону и угол
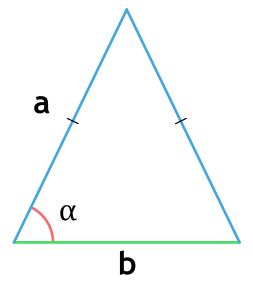
{S = dfrac{1}{2} cdot a cdot b cdot sin{(alpha)}}
a – боковая сторона равнобедренного треугольника
b – основание равнобедренного треугольника
α – угол между основанием и боковой стороной
Площадь равнобедренного треугольника через основание и высоту
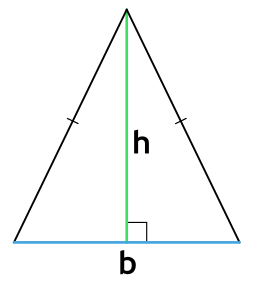
{S = dfrac{1}{2} cdot b cdot h}
b – основание равнобедренного треугольника
h – высота, проведенная к основанию равнобедренного треугольника
Площадь равнобедренного треугольника через боковые стороны и угол между ними
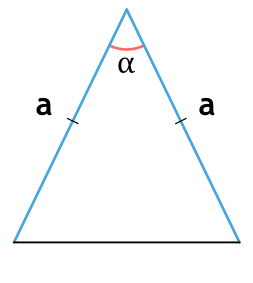
{S = dfrac{1}{2} cdot a^2 cdot sin(alpha)}
a – боковые стороны равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами

{S = dfrac{b^2}{4 cdot tg {( dfrac{alpha}{2} )}}}
b – основание равнобедренного треугольника
α – угол между боковыми сторонами
Площадь равностороннего треугольника
Равносторонний треугольник – треугольник, у которого все стороны равны.
Площадь равностороннего треугольника через сторону

{S = dfrac{sqrt{3} cdot a^2}{4}}
a – сторона равностороннего треугольника
Площадь равностороннего треугольника через высоту
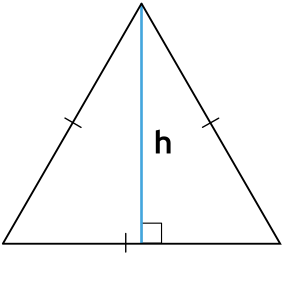
{S = dfrac{h^2}{sqrt{3}}}
h – высота равностороннего треугольника
Площадь равностороннего треугольника через радиус описанной окружности

{S = dfrac{3 sqrt{3} cdot R^2}{4}}
R – радиус описанной окружности
Площадь равностороннего треугольника через радиус вписанной окружности

{S = 3 sqrt{3} cdot r^2}
r – радиус описанной окружности
Примеры задач на нахождение площади треугольника
Задача 1
Найдите площадь треугольника со сторонами 13 14 15.
Решение
Для решения задачи воспользуемся формулой Герона.
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}
Для начала нам необходимо найти полупериметр p:
p= dfrac{a+b+c}{2}p= dfrac{13+14+15}{2}= dfrac{42}{2} = 21
Теперь можем подставить его в формулу Герона и найти ответ:
S = sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)} = sqrt{21 cdot (21-13) cdot (21-14) cdot (21-15)} = sqrt{21 cdot (8) cdot (7) cdot (6)} = sqrt{21 cdot 336} = sqrt{7056} = 84 : см^2
Ответ: 84 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 100.
Решение
Воспользуемся формулой.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 28 cdot sqrt{100^2 – 28^2} = dfrac{1}{2} cdot 28 cdot sqrt{10000 – 784} = dfrac{1}{2} cdot 28 cdot sqrt{9216} = dfrac{1}{2} cdot 28 cdot 96 = 14 cdot 96 = 1344 : см^2
Ответ: 1344 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь прямоугольного треугольника если его катет и гипотенуза равны соответственно 15 и 17.
Решение
Задача аналогична предыдущей, поэтому решение очень похоже.
S = dfrac{1}{2} cdot a cdot sqrt{c^2 – a^2} = dfrac{1}{2} cdot 15 cdot sqrt{17^2 – 15^2} = dfrac{1}{2} cdot 15 cdot sqrt{289 – 225} = dfrac{1}{2} cdot 15 cdot sqrt{64} = dfrac{1}{2} cdot 15 cdot 8 = 15 cdot 4 = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 4
Найдите площадь прямоугольного треугольника, если гипотенуза его равна 40 см а острый угол равен 60°.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{1}{4} cdot c^2 cdot sin{(2 alpha)} = dfrac{1}{4} cdot 40^2 cdot sin{(2 cdot 60°)} = dfrac{1}{4} cdot 1600 cdot sin{(120°)} = 400 cdot dfrac{sqrt{3}}{2} = 200 sqrt{3} : см^2 approx 346.41016 : см^2
Ответ: 200 sqrt{3} : см^2 approx 346.41016 : см^2
Проверка .
Задача 5
Найдите площадь равнобедренного треугольника, если боковая сторона равна 7 см а основание 4 см.
Решение
В этой задаче используем формулу для нахождения площади равнобедренного треугольника через основание и боковую сторону.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{4}{4} sqrt{4 cdot 7^2 – 4^2} = sqrt{4 cdot 49 – 16} = sqrt{196 – 16} = sqrt{180} = sqrt{36 cdot 5} = 6sqrt{5} : см^2 approx 13.41641 : см^2
Ответ: 6sqrt{5} : см^2 approx 13.41641
Проверка .
Задача 6
Найдите площадь равнобедренного треугольника, если его основание равно 30, боковая сторона равна 17.
Решение
Решим эту задачу по анологии с предыдущей.
S = dfrac{b}{4} sqrt{4a^2 – b^2} = dfrac{30}{4} sqrt{4 cdot 17^2 – 30^2} = dfrac{30}{4} sqrt{4 cdot 289 – 900} = dfrac{30}{4} sqrt{1156 – 900} = dfrac{30}{4} sqrt{256} = dfrac{30}{4} cdot 16= 30 cdot 4 = 120 : см^2
Ответ: 120 см²
Проверка .
Задача 7
Найдите площадь равностороннего треугольника со стороной 12 см.
Решение
Используем для решения задачи формулу.
S = dfrac{sqrt{3} cdot a^2}{4} = dfrac{sqrt{3} cdot 12^2}{4} = dfrac{sqrt{3} cdot 144}{4} = 36 sqrt{3} : см^2 approx 62.35383 : см^2
Ответ: 36 sqrt{3} : см^2 approx 62.35383 : см^2
Проверка .
