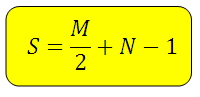Как найти площадь фигур по клеточной бумаге

Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам). Какие есть формулы? Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см). Формула, о которой идет речь, называется формула Пика. Выглядит она вот так: И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N – количество внутренних узлов. Приведем пример, возьмем геометрическую фигуру параллелограмм: Внутренние узлы – синие – N – их у нас 20. Внешние узлы – красные – М – их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов. Складываем 9 + 20 и вычитаем единицу: 20 + 9 – 1 = 28 см². Еще один пример: S = 14/2 + 43 – 1 = 49 см². система выбрала этот ответ лучшим Ксарф­акс [156K] 6 лет назад  Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь. Площадь фигуры по клеточкам Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика. Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе. Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных. Площадь фигуры по клеточкам находится по формуле: N – количество узлов, которые находятся внутри фигуры. M – количество узлов, которые находятся на границах (на вершинах и сторонах). Примеры нахождения площади по клеточкам 1) Найдём площадь треугольника. Будем считать, что одна клетка – это 1 см. Отметим внутренние узлы и узлы, которые находятся на границах. N = 7 (внутренние). M = 8 (узлы на границах). Площадь треугольника S = 7 + 8/2 – 1 = 10 см². 2) Найдём площадь трапеции по клеточкам, одна клетка – это 1 см. Отметим все узлы и подсчитаем их количество. N = 11 (внутренние). M = 12 (узлы на границах). Площадь трапеции S = 11 + 12/2 – 1 = 16 см². 3) Найдём площадь произвольного многоугольника. Одна клетка – это 1 см. Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество. N = 6 (внутренние узлы). M = 8 (узлы на границах). Площадь многоугольника S = 6 + 10/2 – 1 = 10 см². Марин­а Волог­да [294K] 3 года назад  Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура. Вот пример таких задач: Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек. Возьмем простой пример, необходимо вычислить площадь вот такого треугольника: Вспоминаем правило: Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину. Подставляем к формуле: S = 1/2 х 2 х 6 = 6 см2. Считаем по клеточкам, подставляя формулу Пика: Целых клеточек у нас 3. Теперь считаем, сколько не целых: 6. Делим их на 2. S = 3 + 6:2 = 6 см2. А теперь высчитываем по формуле Пика: количество узлов сетки внутри – 2, количество узлов сетки, лежащих на границах – 10. Подставляем к формуле и получаем – 2 + 10:2 – 1 = 6 см2. Теперь давайте рассмотрим вот такой треугольник: Чтобы найти площадь, вспоминаем правило: Считаем клеточки и подставляем в формулу: S = 1/2 х 2 х 6 = 6 см2. А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2. Пробуем сделать по формуле Пика: количество узлов сетки внутри – 3, количество узлов сетки, лежащих на границах – 8. Подставляем к формуле и получаем – 3 + 8:2 – 1 = 6 см2. Enot-Nina [110K] 3 года назад  Найти площадь геометрической фигуры можно самыми разными способами: Самый простой вариант – это вручную посчитать клеточки – целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые. Есть еще один способ – это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов – точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов – по контуру фигуры. Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам: Барха­тные лапки [382K] 3 года назад  Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В – количество узловых клеточек внутри фигуры, Г – количество узлов на границе . Узлы – пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 – 1 Считаем точки на рисунке и подставляем в формулу. – 10 + 7/2 -1 = 12,5. Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах. Ann Luka [2.8K] 6 лет назад  Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек – это и будет правильный ответ. Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток. Outli­ne [18.3K] 3 года назад  Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика: S=В + Г / 2 − 1 В этой формуле буквенные обозначения означают следующее: В — количество целочисленных точек внутри многоугольника; Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника; S – площадь фигуры. Здесь используется понятие “целочисленные” – это те, точки, которые расположены на пересечениях сетки (в ее узлах). Для примера, найдем площадь треугольника: Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки: В=12, Г=4. Исходя из подсчетов определяем площадь треугольника по формуле: S=В+Г/2-1=12+2-1=13. Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников: S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15. Исходя из полученных данных, S белого треугольника равна 13: S=36-6-15-2=13. Kriti­kSPb [93.6K] 3 года назад  Подсчет клеточек – дело полезное. С их помощью можно найти площадь геометрической фигуры. Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году. Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х. На теорему Пика есть задания в ЕГЭ. 12777­1 [272K] 3 года назад  Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом: Площадь = В + Г/2 – 1, где: В – количество целочисленных точек внутри многоугольника. Г – количество целочисленных точек на границе многоугольника. Теперь разберемся на примере, у нас есть такой пример: Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой: 11+12/2-1=16 кв.см. Бекки Шарп [71.2K] 3 года назад  Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где В – количество внутренних узловых точек, Г – количество граничных узловых точек, Вот такая фигура у нас – Считаем точки и подставляем в формулу: S = 17 + 14/2 – 1 = 23 Ответ мы получаем в квадратных единицах, то есть клеточках. Знаете ответ?

Почему бы просто не считать клеточки?

Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.

Вот, например, трапеция:

Посчитаем клеточки: их всего 46, верно?

Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)

Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…

Как всё это учитывать?

Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.

А жёлтые сколько занимают? Постарайтесь ответить сами.

Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.

Итак, 2 жёлтых куска = 1 клетка.

Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки. 

Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.

Итого клеток: ( 1 + 2 + 39 = 42).

Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.

Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).

Вычислите площадь простых фигур тремя способами

Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.

Вычислите площадь произвольных фигур по формуле Пика

Вычислите самостоятельно площади фигур с помощью формулы Пика:

Посчитайте площадь корабля и котика по формуле Пика

Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!

Фигуры с отверстиями — посчитайте площади двумя способами

Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?

Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?

Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).

А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика

Сосчитай сам и проверь.

Что получилось?

У меня снова на 1 меньше.

Так может быть просто формулу немного «подкрутить»? Нет!

Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.

Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).

И тогда

( displaystyle {{S}_{осн}}) — это площадь правильного треугольника ( displaystyle ABC).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» — это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle {{S}_{Delta ASB}}).

Пользуясь основной формулой площади и теоремой Пифагора, находим

( displaystyle S={{a}^{2}}sqrt{3}).

ФЕСТИВАЛЬ ТВОРЧЕСКИХ ОТКРЫТИЙ И ИНИЦИАТИВ «ЛЕОНАРДО»

Секция «Математика»

Способы нахождения площадей фигур или задачи на клетчатой бумаге

Выполнила: Кебина Диана Сергеевна, 6 Г класс, МБОУ «Гимназия № 9 «Гармония» г. Горно-Алтайска» Научный руководитель: Боделукова Ольга Петровна учитель математики, первой квалификационной категории, МБОУ «Гимназия № 9 «Гармония» г. Горно-Алтайска»

г. Горно-Алтайск,

2021 г.

ОГЛАВЛЕНИЕ

Введение..…………………………………………………………..… 3

1. Основная часть:

   1. Площадь фигуры как сумма площадей её частей……………. 4

   2. Площадь фигуры как часть площади прямоугольника……… 5

   3. Формула Пика…………………………………………………. 6-7

   4. Задачи с практическим содержанием………………………… 8

   5. Задачи из государственной итоговой аттестации……………. 8

Заключение………………………………………………………….. .. 9

Список литературы и источников………………………………. …. 10

Приложение……………………………………………………… …. 11

1. Введение

Ещё в начальной школе мы изучали формулы нахождения площадей прямоугольника S = a ∙ b, квадрата S = a ∙ a и прямоугольного треугольника S = (a ∙ b) / 2.

При изучении математики в 5 классе мы тоже использовали эти формулы для вычисления площадей фигур. А также изучили основные свойства площадей: равные фигуры имеют равные площади; площадь фигуры равна сумме площадей её частей. В нашем учебнике встречаются задачи на клетчатой бумаге на нахождение площадей фигур. [1]

Мне стало очень интересно, какие способы решения таких задач существуют. При изучении литературы я обнаружила, что их достаточное количество. Я решила изучить их и проверить какой из них самый результативный, т.е. малозатратный по времени и дает безошибочный результат.

Проблема: Вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части?

Цель работы: Исследование рациональности использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.

Задачи:

1. Изучить способы решения задач на клетчатой бумаге.

2. Выбрать наиболее оптимальный способ.

Объект исследования: Задачи на вычисление площади различных фигур на клетчатой бумаге.

Предмет исследования: Способы вычисления площади фигур на клетчатой бумаге.

Методы исследования: 1) теоретический: изучение литературы;

2) эмпирический: анализ, сравнение; 3) математический: построение фигур, вычисления.

Актуальность: при решении задач по математике и геометрии часто встречаются задачи, где нужно вычислить площадь фигур.
Задания на нахождение площади фигур на клетчатой бумаге встречаются в КИМах ОГЭ и ЕГЭ. А на экзамене очень важно решить задание правильно и при решении затратить как можно меньше времени.

Рассмотрим основные способы решения таких задач.

1. Основная часть

   1. Площадь фигуры как сумма площадей её частей

Задача 1. Найдём площадь фигуры АВСD (рисунок 1). Если клетки размером 1х1см.

Р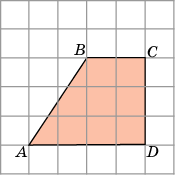 азобьем фигуру АВСD на части (1 и 2).

По свойству площадей:

2

S = S1 + S2 = (2∙3):2 + 3∙2 = 3 + 6 = 9 см.²

1

Ответ: 9 см.²

Рисунок 1.

Задача 2. Найдём площадь фигуры АВСD (рисунок 2). Если клетки размером 1х1см.

Р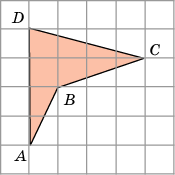 азобьем фигуру АВСD на части (1, 2, 3 и 4).

П

1

о свойству площадей:

2

3

4

S = S1 + S2 + S3 + S4 = (1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 = 2 + 1,5 + 1 + 1 = 5,5 см.²

Ответ: 5,5 см.²

Рисунок 2.

З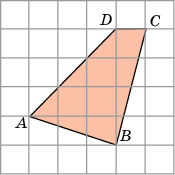 адача 3. Найдём площадь фигуры АВСD (см.рис.3). Если клетки размером 1х1см.

1

Разобьем фигуру АВСD на части (1, 2 и 3).

П

2

о свойству площадей:

S = S1 + S2 + S3 =

=

3

(1∙4):2 + (3∙3):2 + (1∙3):2 =

= 2 + 4,5 + 1,5 = 8 см²

Ответ: 8 см²

Рисунок 3.

1. Площадь фигуры как часть площади прямоугольника

Задача 4. Найдём площадь фигуры АВСD (рисунок 4). Если клетки размером 1х1см.

О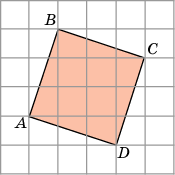 пишем около фигуры АВСD прямоугольник.

И

1

4

з площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):

S

2

3

= Sпр – S1 – S2 – S3 – S4 =

= 4∙4 – (3∙1):2 – (3∙1):2 – (3∙1):2 – (3∙1):2 = 16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см.²

Рисунок 4. Ответ: 10 см.²

Задача 5. Найдём площадь фигуры АВСD (рисунок 5). Если клетки размером 1х1см.

О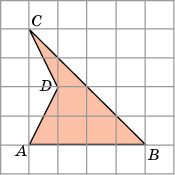 пишем около фигуры АВСD прямоугольник.

И

1

2

3

з площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):

S = Sпр – S1 – S2 – S3 =

= 4∙4 – (4∙4):2 – (2∙1):2 – (2∙1):2 = 16 – 8 – 1 – 1 =

= 6 см.²

Рисунок 5 Ответ: 6 см.²

Задача 6. Найдём площадь фигуры АВСD (рисунок 6). Если клетки размером 1х1см.

О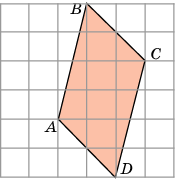

4

пишем около фигуры АВСD прямоугольник.

И

1

з площади прямоугольника вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = Sпр – S1 – S2 – S3 – S4 =

=

3

3∙6 – (4∙1):2 – (2∙2):2 – (4∙1):2 – (2∙2):2 =

=

2

18 – 2 – 2 – 2 – 2 = 10 см.²

Рисунок 6 Ответ: 10 см.²

1. Формула Пика

Л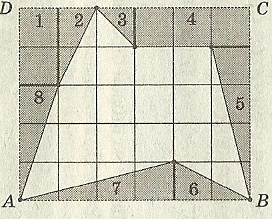 инии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.

Нарисуем на листе многоугольник с вершинами в узлах (рисунок 7) и найдем его площадь. [2] Оказывается площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.

Рисунок 7.

Пусть АВСD – прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки (рисунок 8). Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки, а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника

Рисунок 8. S = В + + 4 · = В + – 1.

Для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, установлена формула S = В + – 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [4]

Она секретной не является. Информация о ней в интернете имеется. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим. Автор этой формулы австрийский математик Георг Пик (приложение 1). [8]

Можно убедиться в том, что формула Пика верна для всех рассмотренных выше примеров.

Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Рассмотрим применение формулы Пика на примерах:

Задача 7. Найдем площадь треугольника (рисунок 9).

Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника: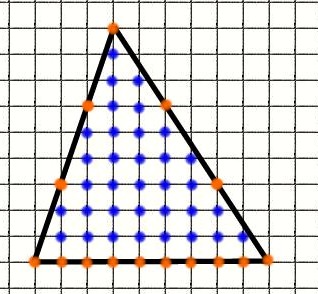

В = 34 (обозначены синим),

Г = 15 (обозначены оранжевым).

S= 34 + 15/2 – 1 = 40,5 кв.ед.

Ответ: 40,5 кв.ед

Рисунок 9.

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [9]

Задача 8. Найдем площадь пятиугольника (рисунок 10).

О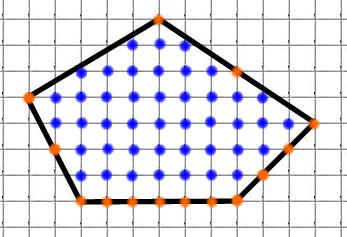 тметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:

В = 43 (обозначены синим),

Г = 14 (обозначены оранжевым).

S= 43 + 14/2 – 1 = 49 кв.ед.

Ответ: 49 кв.ед.

Рисунок 10.

Конечно, есть ещё способы нахождения фигур на клетчатой бумаге. Например, можно просто сосчитать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.

Можно находить площади фигур на клетчатой бумаге, используя формулы площади произвольного треугольника, трапеции, ромба, параллелограмма. Но для этого нужно знать эти формулы и уметь ими пользоваться.

И есть такие фигуры на клетчатой бумаге, для которых эти формулы применить очень трудно, да и затратно по времени.

1. Задачи с практическим содержанием

Поможет нам формула Пика и для решения геометрических задач с практическим содержанием, когда объект изображен на клетчатой бумаге в масштабе. [4]

Задача 9. Найдите площадь лесного массива (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 200 м (рисунок 11).

Н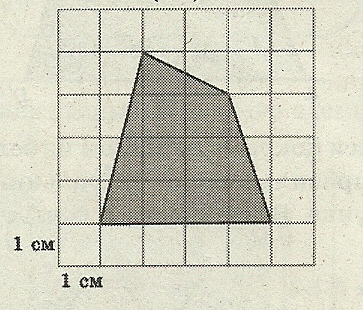 айдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S= В + – 1

В = 8, Г = 7. S = 8 + 7/2 – 1 = 10,5 см.²

Т.к. 1 см² – 200² м.², то

Sмассива = 40000 · 10,5 = 420 000 м.²

Рисунок 11. Ответ: 420 000 м.²

Задача 10. Найдите площадь поля (в м²), изображённого на плане с квадратной сеткой 1 × 1см в масштабе 1 см – 100 м (рисунок 12).

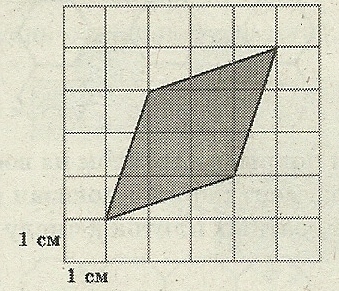
Найдём S площадь четырёхугольника, изображённого на клетчатой бумаге по формуле Пика: S = В + – 1. В = 7, Г = 4.

S = 7 + 4/2 – 1 = 8 см.², т.к. 1 см² – 100² м.², то

Sполя = 10000 · 8 = 80 000 м.²

Рисунок 12. Ответ: 80 000 м.²

1. Задачи из государственной итоговой аттестации.

Задача 11. Найти площадь фигуры (рисунок 13):

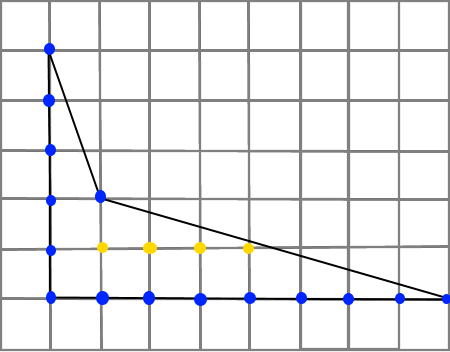
Желтые точки – точки внутри фигуры: В = 4. Синие точки – точки на границах: Г=15. S = В + – 1 S = 4 + 15/2 – 1 = 4 + 7,5 – 1 = 10,5 кв.ед. Ответ: 10,5 кв.ед.

Рисунок 13.

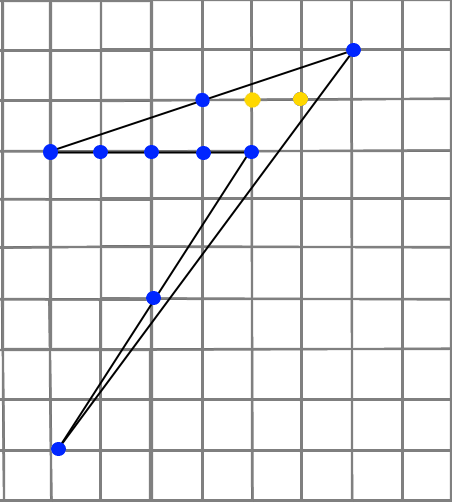
Задача 12. Найти площадь фигуры (рисунок 14):

Рисунок 14.

Желтые точки – точки внутри фигуры: В=2. Синие точки – точки на границах: Г=9. S = В + – 1 S = 2+ 9/2 – 1 = 2 + 4,5 – 1 = 5,5 кв.ед. Ответ: 5,5 кв.ед.

1. Заключение

Вернемся к задаче 2.

Задача 2. Найдём площадь фигуры АВСD. Если клетки размером 1х1см.

Р азобьем фигуру АВСD на части (1, 2, 3 и 4).

П

1

о свойству площадей:

2

3

S = S1 + S2 + S3 + S4 =

=

4

(1∙4):2 + (1∙3):2 + 1∙1 + (1∙2):2 =

= 2 + 1,5 + 1 + 1 = 5,5 см.²

Ответ: 5,5 см.²

Найдем площадь по формуле Пика: В= 3; Г=7. S = В +Г/2 – 1.

S = 3+7/2 -1= 5,5 см²

Вывод: Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге. Я рассмотрела некоторые из них. Задачи, поставленные в самом начале моей работы, выполнены. Все способы нахождения площадей фигур на клетчатой бумаге хороши, но самым результативным оказался способ решения по формуле Пика!

Формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге: 

1. Для вычисления площади многоугольника, нужно знать всего одну формулу:

2. Формула Пика очень проста для запоминания.

3. Формула Пика очень удобна и проста в применении.

4. Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.

1. Список литературы и источников

1. Мерзляк А.Г. Математика 5 класс. Учебник для общеобразовательных школ. – М., «Вентана-Граф», 2016.

2. Жарковская Н. М., Рисс Е. А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс] – URL: http://mat.1september.ru/2009/23/gazeta_23_09.pdf (дата обращения 18.11.2020г.)

3. ФИПИ. Открытый банк заданий ЕГЭ 2020 по математике. – [Электронный ресурс] – URL: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege (дата обращения 18.11.2020г.)

4. Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2013.

5. Смирнова И. М., Смирнов В. А. Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2015.

6. Сдам ГИА. [Электронный ресурс]- URL: https://ege.sdamgia.ru/

7. Википедия. Формула Пика. – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/%D4%EE%F0%EC%F3%EB%E0_%CF%E8%EA%E0 (дата обращения 18.11.2020г.)

8. Википедия. Пик. Георг. – [Электронный ресурс] – URL: https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D0%B3 (дата обращения 18.11.2020г.)

9. Математика? Легко!!! Площади фигур. – [Электронный ресурс] – URL: http://matematikalegko.ru/category/plocshadi-figur (дата обращения 18.11.2020г.)

1. Приложение

Приложение 1

Г еорг Алекса́ндр Пик  (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. 16 апреля 1880 года под руководством Лео Кёнигсбергера  Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти  хабилитацию. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик  Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа  и  дифферен-циальной геометрии, эллиптических и абелевых функций, теории  дифференциальных уравнений  и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика – Неванлинны,  лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [8]

14

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри  треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно  это делать и таким образом. 

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см.  Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Вычисление площадей фигур на клетчатой бумаге разными способами

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Ещё  в начальной  школе мы освоили формулы нахождения площадей прямоугольника S = a • b, квадрата S = a2 и прямоугольного треугольника 

S = (a • b) : 2.

При  изучении  математики  в 5 классе  мы  тоже  применяли  эти формулы  для  вычисления  площадей  фигур. А  также  освоили  основные  свойства  площадей:  равные  фигуры  имеют  равные  площади;  площадь  фигуры  равна  сумме  площадей  её  частей.  В  учебнике  по  математике  для      5 класса  есть  задачи  на  клетчатой  бумаге  на  нахождение  площадей  фигур. [1]

Мне  стало  очень  интересно,  какие  способы  решения  таких  задач существуют. При  изучении  литературы  выявилось,  что  их  достаточное количество. Я  решила  изучить  их  и  проверить  какой  из  них  самый  результативный, т.е. малозатратный  по  времени  и  дает  безошибочный  результат.

Проблема: Существует ли самый результативный способ нахождения площади фигуры на клетчатой бумаге?

Гипотеза: Самым эффективным способом вычисления площадей на клетчатой бумаге будет способ по формуле Пика.

Цель работы: Изучить способы решения задач на клетчатой бумаге и выбрать самый наилучший.

Задачи:

1. Изучить литературу по теме исследования.
2. Выбрать  и изучить способы нахождения площадей фигур на клетчатой бумаге.
3. Подобрать задачи.
4. Провести эксперимент.
5. Сделать выводы.

Объект исследования: фигуры на клетчатой бумаге.

Предмет исследования: площадь фигур.

Методы исследования:

1) теоретический – изучение литературы;

2) эмпирический – эксперимент, анализ, сравнение;

3) математический – построение таблиц, вычисления.

Актуальность данной темы выбрана желанием показать разнообразие способов решения одной задачи. При решении олимпиадных задач я часто находилась в затруднении при встрече с задачами на клетчатой бумаге. А увидев такие задачи в КИМах ЕГЭ, ОГЭ приняла решение исследовать задачи на клетчатой бумаге и помочь выпускникам освоить их, чтобы как можно меньше времени тратить на выполнение таких заданий.

Рассмотрим основные способы решения таких задач в исследовательской  работе.

Основная часть

2.1  Площадь фигуры как сумма площадей её частей

Задача 1. Найдём площадь фигуры АВСD (см.рис.1). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1 и 2).

По свойству площадей:

 S = S1  + S2  = (2•3):2 + 3•2  = 3 + 6 = 9 см²

Ответ: 9 см²

Рис.1

Задача 2. Найдём площадь фигуры АВСD (см.рис.2). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1, 2, 3 и 4).

По свойству площадей:

S = S1  + S2  + S3 + S4 =

= (1•4):2 + (1•3):2 + 1•1 + (1•2):2  =

= 2 + 1,5 + 1 + 1 = 5,5 см²

Ответ: 5,5 см²

Рис.2

Задача 3. Найдём площадь фигуры АВСD (см. рис.3). Если клетки размером 1х1см.

Разобьем фигуру АВСD на части (1, 2 и 3).

По свойству площадей:

S = S1  + S2  + S3 = (1•4):2 + (3•3):2 + (1•3):2  = 2 + 4,5 + 1,5 = 8 см²

Ответ: 8 см²

Рис.3

2.1  Площадь фигуры как часть площади прямоугольника

Задача 4. Найдём площадь фигуры АВСD (см. рис.4). Если клетки размером 1х1см.

Опишем около фигуры АВСD прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = Sпр  – S1 – S2 – S3 – S4  =

= 4•4 – (3•1):2 – (3•1):2 – (3•1):2 – (3•1):2 =

=16 – 1,5 – 1,5 – 1,5 – 1,5 = 10 см2.  Ответ: 10 см²  

Рис.4    

Задача 5. Найдём площадь фигуры АВСD (см. рис.5). Если клетки размером 1х1см.

Опишем около фигуры АВСD прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур (1, 2 и 3):

S = Sпр  – S1 – S2 – S3 = 

= 4•4 – (4•4):2 – (2•1):2 – (2•1):2  = 16 – 8 – 1 – 1 =

= 6 см².  Ответ: 6 см²

Рис. 5

Задача 6. Найдём площадь фигуры АВСD (см.рис.6). Если клетки размером 1х1см.

Опишем около фигуры АВСD  прямоугольник.
Из площади прямоугольника вычтем площади полученных простых фигур (1, 2, 3 и 4):

S = Sпр  – S1 – S2 – S3 – S4  =

= 3•6 – (4•1):2 – (2•2):2 – (4•1):2  – (2•2):2 =

= 18 – 2 – 2 – 2 – 2 = 10 см².  Ответ: 10 см²

2.3  Формула Пика

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток – узлы этой сетки.

Нарисуем на листе многоугольник с вершинами в узлах (рис. 7) и найдем его площадь. [2]

Оказывается площади многоугольников, вершины которых  расположены в узлах сетки, можно  проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника.

Рис. 7

Рис. 8   

Пусть АВСD – прямоугольник с вершинами  в узлах и сторонами, идущими по линиям сетки (рис.8). Обозначим через В – количество узлов, лежащих внутри прямоугольника, а через Г – количество узлов на его границе. Сместим сетку на полклетки вправо и полклетки вниз. Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещённой сетки,  а каждый из Г узлов – 4 граничных не угловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника вычисляется по формуле:

S = В +  4 ·  = В +  – 1.

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, освоили формулу  S = В +  – 1. Оказывается, эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки! Это и есть формула Пика. [5]

Она секретной не является. Информация о ней в интернете имеется. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим. Автор этой формулы австрийский математик Георг Пик (приложение 1). [2]  

Можно убедиться в том, что формула Пика верна для всех рассмотренных выше примеров. Оказывается, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

Рассмотрим применение формулы Пика на примерах:

Задача 7.  Найдем площадь треугольника (см. рис.9). Отметим узлы (пересечение линий) на границе треугольника и внутри треугольника:

В = 34 (обозначены черным), Г = 15 (обозначены серым).

S= 34 + 15/2 – 1 = 40,5 ед²   Ответ: 40,5

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. [7]

Рис.9

Задача 8. Вычислим площадь пятиугольника (см.рис.10).

Отметим узлы (пересечение линий) на границе пятиугольника и внутри пятиугольника:

В = 43 (обозначены черным),

Г = 14 (обозначены серым).

S= 43 + 14/2 – 1 = 49 ед²   Ответ: 49.

Рис.10

Конечно, есть ещё способы нахождения фигур на клеточной бумаге. Например, можно просто считать количество целых клеток внутри фигуры, а из оставшихся кусочков «складывать» целые клетки, но это довольно долго и трудно, особенно если фигура сложной формы.

Можно находить площади фигур на клеточной бумаге, используя формулы площади произвольного треугольника, трапеции, ромба, параллелограмма. Но для этого нужно знать эти формулы и уметь ими пользоваться.

И есть такие фигуры на клеточной бумаге, для которых эти формулы применить очень трудно, да и затратно по времени. А на экзамене по математике в 9-м и в 11-м классе каждая минута дорога!

2.4  Эксперимент и исследование

Мы решили провести эксперимент для того, чтобы выяснить какой из рассмотренных способов является самым эффективным, т.е. результативным (решение без ошибок) и малозатратным по времени.

Обучающимся 9-го и 11-го классов (13 и 8 человек соответственно) мы показали и объяснили способы нахождения площадей фигур на клетчатой бумаге. Ученики решали задачи с помощью способов описанных в п.2.1, 2.2 (приложение 2) [3], [6], [7].  Каждому нужно было решить по четыре задачи и засечь время их выполнения.

Затем рассказали им о формуле Пика, показали на примерах её применение и предложили решить другие задачи на клетчатой бумаге, но по формуле Пика (снова засекали время).

Результаты эксперимента представлены в таблицах (приложение 3).

Общие результаты эксперимента:

	Затраченное время – среднее значение (мин)	Количество уч-ся, допустивших ошибки	Безошибочных работ
T1	T2	Т3		О1	О2	О3		Б1	Б2	Б3
11 класс (13 учеников)	2,9	2,8	2,0		9	10	9		4	3	4
9 класс (8 учеников)	2,4	2,3	1,4		8	6	3		–	2	5
Всего (21 ученик)	2,7	2,6	1,7		17	16	12		4	5	9

Заключение

Выполненный эксперимент показал, что:

1. Из двух классов почти никто не знал формулу Пика.
2. 17 из 21 учащихся допустили ошибки при вычислении площадей фигур, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей;
3. 16 из 21 учащихся допустили ошибки при вычислении площадей фигур на клетчатой бумаге, используя правило площади фигуры, как части площади прямоугольника;
4. 12 из 21  учащихся допустили ошибки при решении задач, используя формулу Пика;
5. количество ошибок, допущенных при решении задач по формуле Пика, сократилось;
6. количество безошибочных работ увеличилось;
7. время, затраченное на решение по формуле Пика, сократилось.

Существует достаточное количество способов нахождения площадей фигур на клетчатой бумаге. Мы рассмотрели основные из них. Задачи, поставленные в самом начале нашей работой, выполнили. Все способы нахождения площадей фигур на клетчатой бумаге хороши, но самым результативным оказался способ решения по формуле Пика!

Наша гипотеза подтвердилась. А тем выпускникам, которые недостаточно знают формулы площадей фигур или имеют проблемы с геометрией, эта работа – неоспоримая помощь в подготовке к выполнению таких заданий.

Список использованных источников и литературы

1. Виленкин В.Я. Математика 5 класс: учебник для учащихся общеобразовательных школ / В.Я. Виленкин. – М. : Мнемозина, 2016. – 280 с.
2. Смирнова И.М. Геометрия на клетчатой бумаге: учебно-методическое пособие / И.М. Смирнова, В.А. Смирнов – М: Чистые пруды, 2009. – 32 с.
3. Смирнова И.М. Геометрические задачи с практическим содержанием: пособие для учащихся / И.М. Смирнова, В.А. Смирнов – М.: Чистые пруды, 2010. – 136 с.
4. Википедия. Пик. Георг. [Электронный ресурс]. – Режим доступа: https://ru.wikipedia, свободный. – Загл. с экрана.
5. Жарковская Н.М., Рисс Е.А. Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17. – [Электронный ресурс]. – Режим доступа:  http://mat.1september.ru/2009/23/gazeta_23_09.pdf, свободный. – Загл. с экрана.
6. ФИПИ. Открытый банк заданий ЕГЭ 2017-2018 по математике. – [Электронный ресурс]. – Режим доступа: http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege, свобоный. – Загл. с экрана.
7. Математика? Легко!!! Площади фигур. – [Электронный ресурс]. – Режим доступа: https://matematikalegko.ru/category/plocshadi-figur, свободный. – Загл. с экрана.
8.  Фигуры на квадратной решётке – «РЕШУ ОГЭ»: математика. ОГЭ – [Электронный ресурс]. – Режим доступа: https://oge.sdamgia.ru/test?theme=14, свободный. Загл. с экрана.

Приложение 1

Георг Алекса?ндр Пик  (нем. Georg Alexander Pick; 10 августа 1859 г. – 13 июля 1942 г.) – австрийский математик.  В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику.  16 апреля 1880 года под руководством Лео Кёнигсбергера  Пик защитил докторскую диссертацию «О классе абелевых интегралов». В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете. Чтобы получить право чтения лекций, Георгу необходимо было пройти  хабилитацию.  Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете. В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 г., он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры. Преподавательская деятельность в Немецком университете в Праге в 1888 г. Пик получил место экстраординарного профессора математики, затем в 1892г. стал ординарным профессором. В 1910 г. Георг Пик был в комитете, созданном Немецким университетом Праги для рассмотрения вопроса о принятии Альберта Эйнштейна профессором в университет. Пик и физик  Антон Лампа были главными инициаторами этого назначения, и благодаря их усилиям Эйнштейн, с которым Пик впоследствии сдружился, в 1911г. возглавил кафедру теоретической физики в Немецком университете в Праге. Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа  и  дифферен-циальной геометрии, эллиптических и абелевых функций, теории  дифференциальных уравнений  и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика – Неванлинны,  лемма Шварца-Пика. Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. [4]

Приложение 2

Вычислить площадь фигуры, используя одно из свойств площадей – площадь фигуры равна сумме площадей ее частей.

1. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

1. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

1. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

1. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1. 

Вычислить площадь фигуры, используя правило пощади фигуры как части площади прямоугольника.

1. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.

1. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.

1. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.

1. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

Вычислить площадь фигуры, используя формулу Пика.

1. Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
2. Найдите площадь треугольника ABC, считая стороны квадратных клеток равными 1.
3. Найдите площадь трапеции ABCD, считая стороны квадратных клеток равными 1.
4. Найдите площадь четырехугольника ABCD, считая стороны квадратных клеток равными 1.

Приложение 3

Результаты эксперимента в 9-м классе:

	Затраченное время	Количество ошибок
T1	T2	T3		О1	О2	О3
1/9	2,1	2,57	2,0		3	2	4
2/9	1,09	2,36	1,28		3	3	4
3/9	1,38	2,15	1,20		3	1	2
4/9	0,51	1,10	0,50		1	1	0
5/9	6,10	3,50	2,01		2	1	0
6/9	1,10	–	1,03		2	4	0
7/9	1,13	1,52	0,55		2	0	0
8/9	5,35	1,45	2,20		2	0	0
Всего (8 учеников)	2,4	2,3	1,4		8	6	3

Индекс 1 – решение задач, используя одно из свойств вычисления площадей – площадь фигуры равна сумме площадей ее частей.

Индекс 2 – решение задач, используя правило площади фигуры, как части площади прямоугольника.

Индекс 3 – решение задач по формуле Пика.

Результаты эксперимента в 11-м классе:

	Затраченное время		Количество ошибок
T1	T2	T3		О1	О2	О3
1/11	1,00	1,30	1,00		0	0	0
2/11	4,55	3,15	2,10		4	1	0
3/11	3,10	4,00	2,08		4	3	0
4/11	2,55	3,33	2,12		1	1	0
5/11	2,39	2,20	2,03		1	0	1
6/11	2,58	1,44	1,10		2	0	3
7/11	1,59	2,28	3,03		2	2	1
8/11	3,30	3,45	2,50		1	3	4
9/11	3,50	2,44	2,05		3	2	1
10/11	3,50	4,00	1,10		4	2	4
11/11	2,07	3,21	1,30		0	2	3
12/11	3,58	2,06	3,08		0	2	1
13/11	4,15	3,20	3,28		0	3	1
Всего (13 учеников)	2,9	2,8	2,0		17	16	12

Индекс 1 – решение задач, используя одно из свойств вычисления площадей – площадь фигуры равна сумме площадей ее частей.

Индекс 2 – решение задач, используя правило площади фигуры, как части площади прямоугольника.

Индекс 3 – решение задач по формуле Пика.

Просмотров работы: 2110