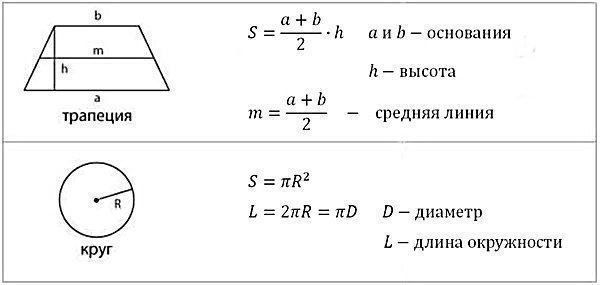Как найти площадь фигуры егэ по математике

Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.

Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.

В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом. 

Всего: 115    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 115    1–20 | 21–40 | 41–60 | 61–80 …

Содержание:

1.      Модуль
1: Основные формулы площадей.

2.      Модуль
2: Методы нахождения площадей.

3.      Модуль
3: Задачи с решением.

4.      Модуль
4: Задачи для закрепления.

5.      Модуль
5: Задачи для самостоятельной работы и зачета.

Модуль
1. Теоретическая часть

1.1.Основные
определения и формулы для площадей фигур.

 Прямоугольник.

Прямоугольником
называется четырехугольник, у которого все углы равны. Все углы в
прямоугольнике прямые, т.е. составляют 90°.Площадь прямоугольника равна
произведению его сторон .

Квадрат.

Квадратом
называется параллелограмм с
прямыми углами и равными сторонами. Квадрат есть частный вид прямоугольника, а
также частный вид ромба. См. также площадь ромба.
Площадь квадрата равна квадрату длины его стороны. Или половине квадрата
диагонали.

;     

Трапеция.

Трапецией называется
четырехугольник, у которого две стороны параллельны, а две другие не
параллельны. Площадь трапеции равна произведению полусуммы ее
оснований на высоту.

 Площадь трапеции равна произведению её средней
линии на высоту. 

Параллелограмм.

Параллелограммом называется
четырехугольник, у которого противоположные стороны попарно
параллельны. Площадь параллелограмма равна произведению его
основания  на высоту.

Площадь параллелограмма равна произведению двух соседних его
сторон на синус угла между ними.  

Правильный многоугольник.

Для
того чтобы вычислить площадь правильного многоугольника его разбивают
на равные треугольники с общей вершиной в центре вписанной окружности. А
площадь правильного многоугольника равна произведению его полупериметра
на радиус вписанной окружности правильного
многоугольника.

Выпуклый четырёхугольник.

 Площадь выпуклого четырёхугольника равна половине произведения
его диагоналей на синус угла между ними.  

 Площадь четырёхугольника, вписанного в окружность, равна корню
квадратному из произведения разностей полупериметра этого четырёхугольника и
всех его сторон

Ромб.

Ромбом называется параллелограмм с
равными сторонами. Квадрат есть частный вид ромба. У квадрата диагонали равны.
См. также площадь квадрата. Площадь
ромба равна половине произведения его диагоналей.

 Площадь ромба равна произведению
квадрата его стороны на синус одного из его углов.  

Сектор.

Сектор
круга, окружности — это часть круга, окружности ограниченная
дугой и двумя радиусами, проведенными к концам дуги. Площадь сектора
круга равна произведению половины длины дуги
сектора  на радиус круга.

 Площадь кругового сектора равна произведению площади единичного
сектора (сектор, соответствующий центральному углу с мерой равной единице) на
меру центрального угла, соответствующего данному сектору ( формулы для случаев градусной и радианной мер центральных
углов).

Окружность.

Окружность есть
геометрическое место точек плоскости, равноудаленных от одной ее точки. Равные
отрезки, соединяющие центр с точками окружности, называются радиусами. Круг
есть часть плоскости, лежащая внутри окружности. Площадь круга равна
произведению полуокружности на радиус.

Площадь
сегмента круга, окружности.

Сегмент круга, окружности — это
часть круга, окружности,
ограниченная дугой и стягивающей ее хордой.

Площадь сегмента круга, окружности
находится, как разность площади сектора и площади равнобедренного треугольника выраженную через угол.

Площадь кольца.

Площадь
кольца через радиусы находится как произведение числаπ на разность
квадратов внешнего и внутреннего радиусов кольца.

Площадь кольца через
диаметры находится как произведение одной четвертой числа π на
разность квадратов внешнего и внутреннего диаметров кольца.

 Площадь кругового кольца равна удвоенному произведению числа
“пи”, среднего радиуса кольца и его ширины. 

Площадь сектора кольца.

Сектор
кольца — это часть круга, окружности ограниченная дугами разных радиусов и
двумя линиями радиусами, проведенными к концам дуги большего радиуса.

Площадь сектора кольца вычисляется
как разность площадей большего и меньшего секторов круга.

Площадь сектора кольца если угол в
градусах, вычисляется как произведение числа π на отношение угла
сектора к углу полной окружности 360° и на разность квадратов большего и
меньшего радиусов.

Площадь треугольника.

Треугольник образуется
соединением отрезками трех точек, не лежащих на одной прямой. При этом точки
называются вершинами треугольника, а отрезки – его сторонами. Площадь
треугольника равна произведению половины основания треугольника на его
высоту.

Площадь треугольника по формуле
Герона равна корню из произведения разностей полупериметра треугольника
(p) и каждой из его сторон.

Если
известно две стороны треугольника и угол
между ними, то площадь данного треугольника вычисляется, как половина
произведения этих сторон умноженная на синус угла между ними.

Если
один из углов прямой, то треугольник – прямоугольный. Площадь прямоугольного
треугольника равна половине произведения катетов треугольника.

Площадь равнобедренного треугольника
вычисляется по классической формуле площади
треугольника — произведение половины
основания треугольника на его высоту. Высоту мы подставим в эту формулу
из формулы высоты равнобедренного
треугольника.

 Площадь
равностороннего треугольника вычисляется по классической формуле площади
треугольника — произведение половины
основания треугольника на его высоту. Высоту мы подставим в эту формулу
из формулы высоты равностороннего
треугольника

Площадь треугольника равна отношению произведения
квадрата его стороны на синусы прилежащих углов к удвоенному синусу
противолежащего угла. 

Площадь треугольника равна отношению произведения
квадрата его высоты на синус угла, из вершины которого проведена эта высота, к
удвоенному произведению синусов двух других углов.

 Площадь треугольника равна произведению квадрата
его полупериметра на тангенсы половин всех углов треугольника. 

 Площадь
треугольника равна отношению произведения всех его сторон к четырём радиусам,
описанной около него окружности. 

 Площадь треугольника равна удвоенному
произведению квадрата радиуса, описанной около него окружности, и синусов всех
его углов.

 Площадь треугольника (многоугольника) равна
произведению его полупериметра и радиуса окружности, вписанной в этот
треугольник (многоугольник). 

 Площадь треугольника равна произведению квадрата
радиуса вписанной окружности на котангенсы половин всех углов треугольника.

Шар и сфера.

 Шаровой,
или сферической поверхностью (иногда просто сферой) называется геометрическое
место точек пространства, равноудаленных от одной точки – центра шара. Площадь
поверхности сферы равна учетверенной площади большого круга:

Куб.

Прямоугольный параллелепипед,
все грани которого – квадраты, называется кубом. Все ребра куба равны,
а площадь поверхности куба равна сумме площадей шести его граней, т.е.площади квадрата со
стороной H умноженной на шесть. Площадь поверхности куба равна.

Конус.

Круглый конус может
быть получен вращением прямоугольного треугольника вокруг
одного из его катетов, поэтому круглый конус называют также конусом вращения.

Боковая площадь поверхности круглого
конуса равна произведению половины окружности основания на образующую.

Цилиндр.

Цилиндрической
поверхностью называется поверхность, образуемая прямой, сохраняющей одно и тоже
направление и пересекающей направляющую линию. Цилиндр —
круговой если в основании его лежит круг. Площадь боковой поверхности круглого
цилиндра равна произведению длины окружности основания
на высоту.

Прямоугольный параллелепипед.

Параллелепипедом
называется призма, основание которой параллелограмм. Параллелепипед
имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые
грани которого — прямоугольники, называется прямым. Прямой параллелепипед у
которого все шесть граней прямоугольники, называется
прямоугольным. Площадь поверхности прямоугольного
параллелепипеда равна удвоенной сумме площадей трех граней этого
параллелепипеда.

Усеченный конус.

Усеченный
конус получится, если в конусе провести сечение, параллельное основанию.
Тело ограниченное этим сечением, основанием и боковой поверхностью конуса
называется усеченным конусом. Боковая площадь поверхности усеченного
конуса вычисляется по формуле.

Шаровой сегмент.

Часть
шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или
сферическим сегментом. Основанием шарового сегмента называется круг ABCD.
Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра,
восстановленного из центра N основания до пересечения с поверхностью
шара. Точка M называется вершиной шарового сегмента. Площадь
поверхности шарового сегмента равняется произведению его высоты на
окружность большого круга шара.

Шаровой
слой.

 Шаровой слой — это часть шара,
заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая
зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания
шарового пояса. Расстояние между основаниями это высота шарового слоя. Кривая
поверхность шарового слоя равна произведению его высоты на окружность
большого круга шара.

Шаровой сектор.

Шаровой
сектор — это часть шара, ограниченная кривой поверхностью шарового
сегмента и конической поверхностью основанием которой служит основание
сегмента, а вершиной — центр шара. Поверхность шарового сектора складывается из
кривых поверхностей шарового сегмента и конуса. Зная радиус основания сегмента
и конуса r при помощи теоремы Пифагора и прямоугольного треугольника
получим высоты сегмента и конуса:

1.2.Справочные
таблицы «Площади плоских фигур, площади поверхности и объема тел вращения»

Модуль
2.  Методы нахождения площади плоских фигур.

Рассмотрим несколько способов нахождения
площади плоских фигур:

·        
формула Пика,

·        
метод обводки.

1.1 
Формула Пика.

Формула, при помощи которой можно находить площадь фигуры
построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник,
многоугольник). Об этой формуле обычно рассказывается применительно к
нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и
вершинах)

N – количество узлов внутри  треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём
площадь треугольника:                     Отметим узлы:

                      

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Пример 1. Найдём площадь параллелограмма:            
Отметим узлы:

               

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Пример 2. Найдём площадь трапеции:                      Отметим
узлы:

                      

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Пример 3. Найдём площадь многоугольника:                     
Отметим узлы:

          

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма,
треугольника проще и быстрее по соответствующим формулам площадей этих фигур.
Но знайте, что можно  это делать и таким образом.  А вот когда дан многоугольник, у которого пять и более углов эта
формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их
площади. При помощи формулы Пика такие задачи решаются за минуту. Например,
найдём площадь фигуры:

                               

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

1.2 Метод обводки.

1. Достроить
   искомую фигуру до прямоугольника.
2. Найти
   площадь всех получившихся дополнительных фигур и площадь самого
   прямоугольника.
3. Из
   площади прямоугольника вычесть сумму площадей всех лишних фигур.

Бывает,
что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:

Вроде бы даже прямоугольный и S=12⋅abS=​2​​1​​⋅ab, но чему
тут равно aa, и чему
равно bb? Как узнать?
Применим для полной ясности оба способа

I способ.

Найдем  по
теореме Пифагора из ΔADC а  по
теореме Пифагора из ΔBCE.
На  листе в клетку легко посчитать длину катетов.

Итак:

Значит, 

Теперь 

 Значит, 

Подставляем в формулу:

Значит, 

II способ 

Нужно окружить нашу фигуру прямоугольником. Вот
так:

Получился
один (нужный) треугольник внутри и три ненужных треугольника снаружи. Но
площади этих ненужных треугольников легко считаются на листе в клетку. Посчитаем
их, а потом просто вычтем из целого прямоугольника.

Итак,                             

Почему же этот способ лучше? Потому что он работает
и для любых фигур. К примеру, нужно посчитать площадь такой фигуры:

Окружаем
ее прямоугольником и снова получаем одну нужную, но сложную площадь и много
ненужных, но простых.

А теперь чтобы найти
площадь  просто находим площадь прямоугольника и вычитаем из него оставшуюся
площадь фигур на клетчатой бумаге.

 

Значит, 

Вот и ответ: 

Модуль
3: Задачи с решением.

1.      Найдите площадь четырёхугольника, изображённого
на клетчатой бумаге 
с размером клетки 1 см * 1 см. Ответ
дайте в квадратных сантиметрах.

Решение:
Разобьём четырёхугольник
диагональю РС на два треугольника. Диагональ эта хороша тем, что идёт под
углом 45° к горизонту. Проведём через точки А и В прямые, параллельные диагонали.

Если на верхней прямой взять любую точку Т, то площадь треугольника РТС окажется равной площади треугольника РАС, т.к. основание РС у них общее,
а высоты, проведённые к РС, равны. Такие же рассуждения
о точке К.

Таким образом, если удачно разместить точки Т и К, как на рисунке
выше, то 

S_ACBP = S_PAC + S_PBC = S_PTC + S_PKC = S_TKP = 0,5·6·3 = 9

Ответ: 9

Возможны и другие варианты
расположения точек Т и
К:

2.      Найдите
площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток
равными единице.

Решение:

Отрежем у данной фигуры все полукруглые части (выпуклости),
которые выходят за рамки квадрата 4·4, и аккуратно упакуем их
на свободные в квадрате места.
Площадь данной причудливой фигуры просто равна площади квадрата 4·4 =
16.
Ответ: 16

3.     
Найдите площадь четырехугольника, изображенного на клетчатой
бумаге с размером клетки 1 см * 1 см. Ответ дайте в квадратных сантиметрах.

Решение:

Опишем около неё прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем
площади полученных простых фигур:

Ответ: 4,5

4.      Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

5.      Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

6.      На
клетчатой бумаге нарисован круг площадью 93. Найдите площадь заштрихованного
сектора.

7.      На
клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 9.
Найдите площадь заштрихованной фигуры.

8.      Найдите
(в см²) площадь S
фигуры, изображенной на клетчатой бумаге с размером
клетки 1см×1см. В ответе запишите S/π.

9.      Найдите
площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

Модуль
4. Задачи для закрепления.

1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными 1.

2.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными 1.

3.
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток равными 1.

4.
Найдите площадь ромба ABCD,
считая стороны квадратных клеток равными 1.

5.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток равными 1.

6.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток равными 1.

7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными 1.

8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными 1.

9.
Найдите площадь S сектора,
считая стороны квадратных клеток равными 1. В ответе укажите .

10.
Найдите площадь S кольца,
считая стороны квадратных клеток равными 1. В ответе укажите .

11.  Найдите площадь треугольника, вершины которого имеют
координаты (1, 1), (4,4), (5, 1).

12.
Найдите площадь четырехугольника, вершины которого имеют координаты (1, 0), (0,
2), (4, 4), (5, 2).

13. Найдите площадь S круга,
изображенного на рисунке. В ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

14. Найдите площадь S круга,
описанного около прямоугольника ABCD. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите   (в кв. см).

15. В ромб ABCD, площадь которого
равна  , вписан круг. Найдите
площадь круга, если размер каждой клетки на чертеже равен 1см *1см.

16.Найдите площадь S круга,
описанного около прямоугольника ABCD. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите  (в кв. см).

17. Найдите площадь круга, описанного
около прямоугольного треугольника АВС. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите  ( в кв. см).

18. Найдите площадь круга, описанного
около прямоугольного треугольника АВС. Размер каждой клетки на чертеже
равен 1см*1см. В ответе укажите  (в кв. см).

19. Найдите площадь S круга,
описанного около четырехугольника, изображенного на рисунке. В ответе укажите  . Размер каждой клетки 1
см × 1 см. Ответ дайте в сантиметрах.

20. Найдите площадь S круга,
описанного около четырехугольника, изображенного на рисунке. В ответе укажите  .  Размер каждой клетки 1
см × 1 см. Ответ дайте в сантиметрах.

21. Найдите площадь S круга,
изображенного на рисунке. В ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

22. Найдите площадь S сектора. В
ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

23. Найдите площадь S заштрихованной
части кругового сектора АОВ. Размер каждой клетки на чертеже равен 1см *1см.
В ответе укажите  (в кв. см).

24.Найдите площадь круга, описанного около
прямоугольника АВСD. Размер каждой клетки на чертеже равен 1см 1см.
В ответе укажите  (в кв. см).

25. Два одинаковых круга касаются друг
друга и сторон прямоугольника ABCD. Найдите площадь одного круга, если площадь
прямоугольника равна  .

26. Две одинаковых окружности касаются
друг друга и сторон прямоугольника ABCD. Найдите периметр прямоугольника, если
длина каждой окружности равна 3,6

27. Диаметр полукруга совпадает со
стороной прямоугольника ABCD, а 3 другие стороны прямоугольника касаются
полукруга. Найдите длину полуокружности, если периметр прямоугольника равен .

 

Модуль
5. Задачи для самостоятельных и зачетных работ.

1.       На клет­ча­той
бу­ма­ге с клет­ка­ми раз­ме­ром 1 см  1 см
изоб­ра­же­на фи­гу­ра (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных
сан­ти­мет­рах.

2.      Най­ди­те пло­щадь квад­ра­та ABCD, счи­тая сто­ро­ны квад­рат­ных
кле­ток рав­ны­ми 1.

3.      Най­ди­те пло­щадь квад­ра­та, вер­ши­ны ко­то­ро­го
имеют ко­ор­ди­на­ты (4;3), (10;3), (10;9), (4;9).

4.      Во сколь­ко раз пло­щадь квад­ра­та, опи­сан­но­го
около окруж­но­сти, боль­ше пло­ща­ди квад­ра­та, впи­сан­но­го в эту окруж­ность?

5.      В пря­мо­уголь­ни­ке рас­сто­я­ние от точки пе­ре­се­че­ния
диа­го­на­лей до мень­шей сто­ро­ны на 1 боль­ше, чем рас­сто­я­ние от нее до
боль­шей сто­ро­ны. Пе­ри­метр пря­мо­уголь­ни­ка равен 28. Най­ди­те мень­шую
сто­ро­ну пря­мо­уголь­ни­ка.

6.      На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­жен па­рал­ле­ло­грамм (см. ри­су­нок).
Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

7.      Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

8.      Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

9.      Най­ди­те пе­ри­метр че­ты­рех­уголь­ни­ка , если сто­ро­ны квад­рат­ных кле­ток равны .

10.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

11.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

12.  Най­ди­те пло­щадь тра­пе­ции, вер­ши­ны ко­то­рой
имеют ко­ор­ди­на­ты (1;1), (10;1), (8;6), (5;6).

13.  Най­ди­те вы­со­ту тра­пе­ции , опу­щен­ную из вер­ши­ны , если сто­ро­ны квад­рат­ных кле­ток равны .

14.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром
1 см  1 см изоб­ра­же­на фи­гу­ра (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

15. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка,
вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (8;0), (10;8), (2;10), (0;2).

16.    Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

17.  Най­ди­те
пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром
клет­ки 1 см  1
см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

18.   Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

19. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на
клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1
см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

20.   Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах

21.   На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 изоб­ражён
тре­уголь­ник. Най­ди­те ра­ди­ус опи­са­ной около него окруж­но­сти.

22.   На клет­ча­той бу­ма­ге на­ри­со­ва­ны два круга. Пло­щадь
внут­рен­не­го круга равна 11. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

23. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, вер­ши­ны
ко­то­ро­го имеют ко­ор­ди­на­ты (1;7), (8;2), (8;4), (1;9).

24.   Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры на ко­ор­ди­нат­ной
плос­ко­сти.

25.  Точки O(0;
0), A(10; 0), B(8; 6), C(2; 6) яв­ля­ют­ся вер­ши­на­ми
тра­пе­ции. Най­ди­те длину ее сред­ней линии DE.

26.  Най­ди­те (в см²) пло­щадь S за­кра­шен­ной фи­гу­ры,
изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). В от­ве­те за­пи­ши­те .

27.   Най­ди­те пло­щадь сек­то­ра круга ра­ди­у­са , цен­траль­ный угол ко­то­ро­го равен 90°

28.  .  Най­ди­те
цен­траль­ный угол сек­то­ра круга ра­ди­у­са , пло­щадь ко­то­ро­го равна . Ответ дайте в гра­ду­сах.

29.  На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь
внут­рен­не­го круга равна 1. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

30.  На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь
внут­рен­не­го круга равна 9. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

Зачет

№1

Найдите площадь окрашенной фигуры,
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

№2

Найдите площадь окрашенной фигуры,
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

№3

В детском саду дети делали аппликации
родителям в подарок. Найдите площадь аппликации (окрашенной фигуры),
изображенной на чертеже. Размер каждой клетки равен 1см*1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

№4  В детском саду дети делали фото- рамки
родителям в подарок. Найдите площадь фото-рамки (окрашенной фигуры),
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

6.

7.

8.

9.

10

А древние египтяне пользовались методами вычисления площадей различных фигур, похожими на наши методы.

В своих книгах «Начала»
известный древнегреческий математик Евклид описывал достаточно большое число способов вычисления площадей многих геометрических фигур. Первые рукописи на Руси, в которых содержатся геометрические сведения, были написаны в $XVI$ веке. В них описаны правила нахождения площадей фигур различных форм.

Сегодня с помощью современных методов можно найти площадь любой фигуры с большой точностью.

Рассмотрим одну из простейших фигур — прямоугольник — и формулу нахождения его площади.

Формула площади прямоугольника

Рассмотрим фигуру (рис. 1), которая состоит из $8$ квадратов со сторонами по $1$ см. Площадь одного квадрата со стороной $1$ см называют сантиметром квадратным и записывают $1 см^2$.

Площадь данной фигуры (рис. 1) будет равна $8 см^2$.

Площадь фигуры, которую можно разбить на несколько квадратов со стороной $1 см$ (например, $p$), будет равна $p см^2$.

Другими словами, площадь фигуры будет равна стольким $см^2$, на сколько квадратов со стороной $1 см$ можно разбить эту фигуру.

Рассмотрим прямоугольник (рис. 2), который состоит из $3$ полос, каждая из которых разбита на $5$ квадратов со стороной $1 см$. весь прямоугольник состоит из $5cdot 3=15$ таких квадратов, и его площадь равна $15 см^2$.

Рисунок 1.

Рисунок 2.

Площадь фигур принято обозначать буквой $S$.

Для нахождения площади прямоугольника нужно его длину умножить на ширину.

Если обозначить буквой $a$ его длину, а буквой $b$ — ширину, то формула площади прямоугольника будет иметь вид:

Определение 1

Фигуры называют равными,
если при наложении их одна на другую фигуры совпадут. Равные фигуры имеют равные площади и равные периметры.

Площадь фигуры можно найти как сумму площадей ее частей.

Пример 1

Например, на рисунке $3$ прямоугольник $ABCD$ разбит на две части линией $KLMN$. Площадь одной части равна $12 см^2$, а другой — $9 см^2$. Тогда площадь прямоугольника $ABCD$ будет равна $12 см^2+9 см^2=21 см^2$. Найдем площадь прямоугольника по формуле:

Как видим, площади, найденные обоими способами, равны.

Рисунок 3.

Рисунок 4.

Отрезок $AC$ делит прямоугольник на два равных треугольника: $ABC$ и $ADC$. Значит площадь каждого из треугольников равна половине площади всего прямоугольника.

Определение 2

Прямоугольник с равными сторонами называется квадратом
.

Если обозначить сторону квадрата буквой $a$, то площадь квадрата будет находится по формуле:

Отсюда и название квадрат числа $a$.

Пример 2

Например, если сторона квадрата равна $5$ см, то его площадь:

Объемы

С развитием торговли и строительства еще во времена древних цивилизаций появилась необходимость в нахождении объемов. В математике существует раздел геометрии, который занимается изучением пространственных фигур, называемый стереометрией. Упоминания об этом отдельном направлении математики встречались уже в $IV$ веке до н.э.

Древними математиками был выведен способ вычисления объема несложных фигур — куба и параллелепипеда. Все сооружения тех времен были именно такой формы. Но в дальнейшем были найдены способы вычисления объема фигур более сложных форм.

Объем прямоугольного параллелепипеда

Если наполнить формочку влажным песком и потом перевернуть, то получим объемную фигуру, которая характеризуется объемом. Если сделать таких фигур несколько с помощью одной и той же формочки, то получатся фигуры, которые имеют одинаковый объем. Если наполнить формочку водой, то объем воды и объем фигуры из песка также будут равными.

Рисунок 5.

Сравнить объемы двух сосудов можно, наполнив один водой и перелив ее во второй сосуд. Если второй сосуд окажется полностью заполненным, то сосуды имеют равные объемы. Если при этом в первой вода останется, то объем первого сосуда больше объема второго. Если при переливании воды из первого сосуда не удается полностью заполнить второй сосуд, значит объем первого сосуда меньше объема второго.

Объем измеряется с помощью следующих единиц:

$мм^3$ — миллиметр кубический,

$см^3$ — сантиметр кубический,

$дм^3$ — дециметр кубический,

$м^3$ — метр кубический,

$км^3$ — километр кубический.

Общий обзор. Формулы стереометрии!

Здравствуйте, Дорогие друзья! В этой статье решил сделать общий обзор задач по стереометрии, которые будут на ЕГЭ по математик
е. Нужно сказать, что задачи из этой группы довольно разнообразны, но не сложны. Это задачи на нахождение геометрических величин: длин, углов, площадей, объёмов.

Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 50% из них решаются элементарно, практически устно.

Остальные требуют небольших усилий, знаний и специальных приёмов. В будущих статьях мы с вами будем рассмотривать эти задачи, не пропустите, подпишитесь на обновление блога.

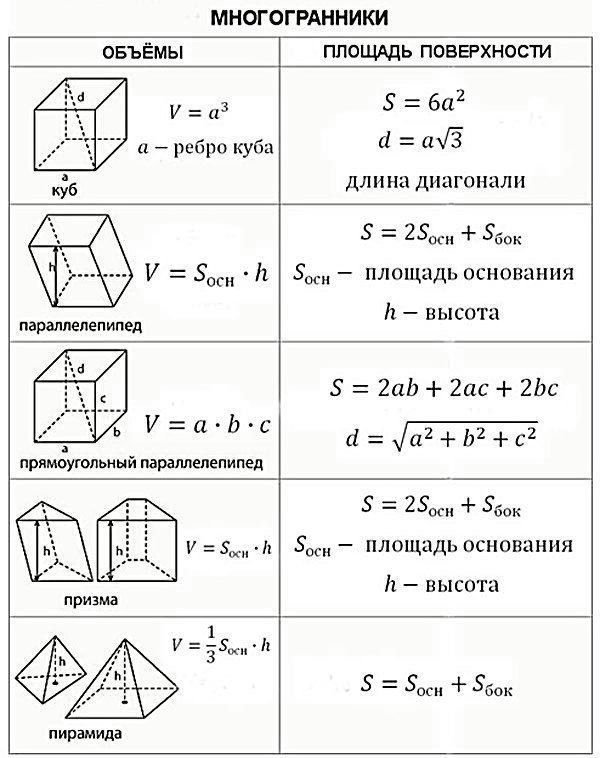
Для решения необходимо знать формулы площадей поверхности и объёмов
параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Сложных задач нет, все они решаются в 2-3 действия, важно «увидеть» какую формулу необходимо применить.

Все нужные формулы представлены ниже:

Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара.

Объем шара
равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Круглый конус может быть получен вращениемпрямоугольного треугольника вокруг одного из его катетов, поэтому круглый конус называт также конусом вращения. См. также Площадь поверхности круглого конуса

Объем круглого конуса
равен трети произведения площади основания S на высоту H:

(H — высота ребра куба)

Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипедимеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.

Объем прямоугольного параллелепипеда
равен произведению площади основания на высоту:

(S — площадь основания пирамиды, h — высота пирамиды)

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.

Объем усеченной пирамиды
равен одной трети произведения высоты h (OS)
на сумму площадей верхнего основания S1 (abcde)
, нижнего основания усеченной пирамиды S2 (ABCDE)
и средней пропорциональной между ними.

n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника — основания правильной пирамиды
h — высота правильной пирамиды

Правильная треугольная пирамида — этомногогранник, у которого одна грань — основание пирамиды — правильныйтреугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.

Объем правильной треугольной пирамиды
равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC)
на высоту h (OS)

a — сторона правильного треугольника — основания правильной треугольной пирамиды
h — высота правильной треугольной пирамиды

Вывод формулы объема тетраэдра

Объем тетраэдра расчитывается по классической формуле объема пирамиды. В нее необходимо подставитьвысоту тетраэдра и площадь правильного (равностороннего) треугольника.

Объем тетраэдра
— равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра

(h — длина стороны ромба)

Длина окружности
p
составляет примерно три целых и одну седьмую длины диаметра круга. Точное отношение длины окружности к ее диаметру обозначается греческой буквой π

В итоге периметр круга или длина окружности вычисляется по формуле

(r — радиус дуги, n — центральный угол дуги в градусах.)

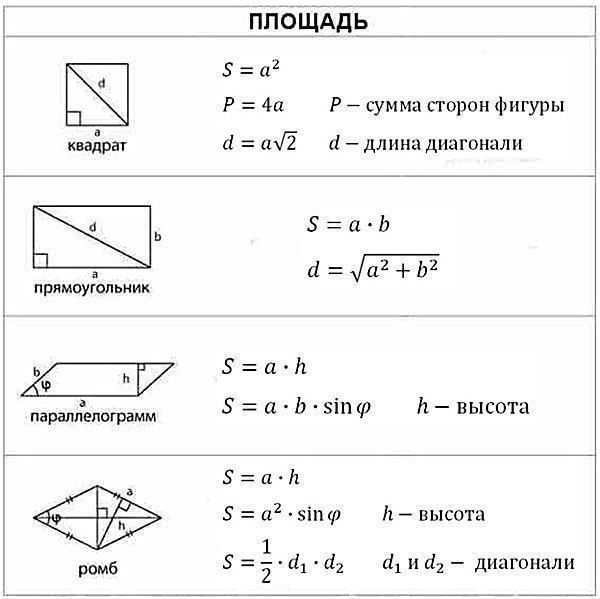
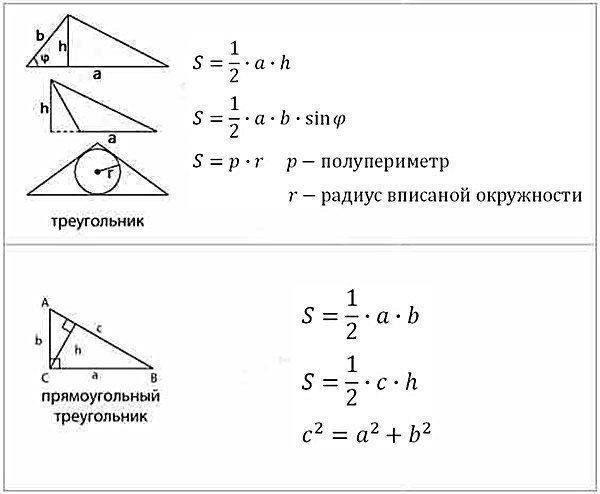
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задание
1

#3043

Уровень задания: Равен ЕГЭ

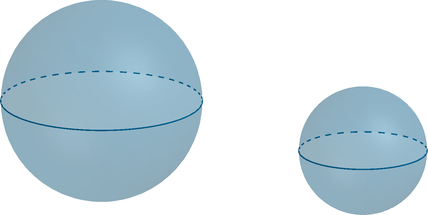
Радиус первого шара в (5) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса (R) ищется по формуле (S=4pi R^2). Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как [dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2}] Так как радиус первого шара больше радиуса второго шара в 5 раз, то (R_1=5R_2). Следовательно, [dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25.] Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Ответ: 25

Задание
2

#3046

Уровень задания: Равен ЕГЭ

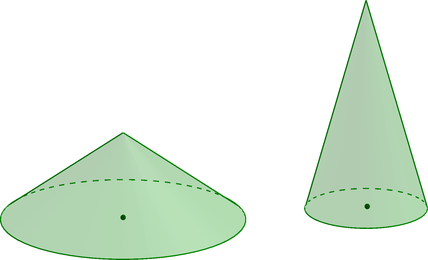
Даны два конуса. Радиус второго конуса в (3) раза больше радиуса первого конуса, а высота второго конуса в (6) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен (18).

Объем конуса с высотой (h) и радиусом основания (R) вычисляется по формуле (V=frac13pi R^2h). Следовательно, объем первого конуса относится к объему второго конуса как [dfrac{V_1}{18}=dfrac{V_1}{V_2}=
dfrac{frac13pi ,R_1^2,h_1}{frac13 pi
,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot
dfrac{h_1}{h_2}] Так как радиус второго в 3 раза больше радиуса первого, то (R_2=3R_1). Так как высота второго в 6 раз меньше высоты первого, то (h_1=6h_2). Следовательно, [dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}=
dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot
18=12.]

Ответ: 12

Задание
3

#3048

Уровень задания: Равен ЕГЭ

Даны два конуса: (K_1) и (K_2). Площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как (4:1). Известно, что радиус (K_1) в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2). Найдите отношение образующей (K_2) к образующей (K_1).

Площадь полной поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi R (R+l)). Тогда площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как [dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)}] Из условия следует, что (R_1=4l_1), (R_2=frac12R_1=2l_1), следовательно, [dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)}
quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5]

Ответ: 0,5

Задание
4

#3044

Уровень задания: Равен ЕГЭ

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в (343) раза больше объема второго шара?

Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}=
left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad
dfrac{R_1}{R_2}=sqrt[3]{343}=7.] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Ответ: 7

Задание
5

#3051

Уровень задания: Равен ЕГЭ

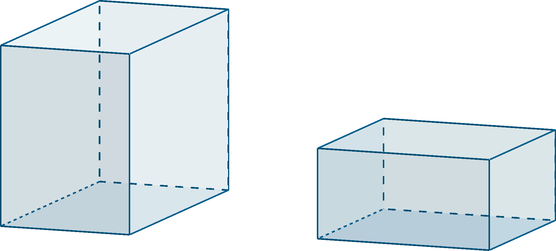
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы (a), (b) и (c) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле (V=abc). Следовательно, объем первого параллелепипеда относится к объему второго как [dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2}] Из условия следует, что (a_1=7a_2), (b_2=2b_1), (c_1=3c_2). Тогда [dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}=
dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot
2}{21}=10.]

Ответ: 10

Задание
6

#3049

Уровень задания: Равен ЕГЭ

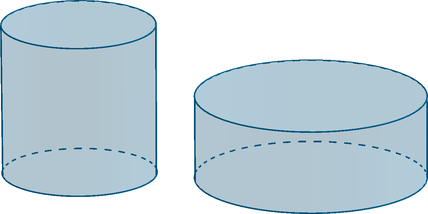
Площадь боковой поверхности первого цилиндра равна (16). Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (S=2pi RH). Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как [dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}=
dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2}] Из условия следует, что (R_2=4R_1), (H_1=5H_2), значит, [dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}=
dfrac14cdot 5=dfrac54] Следовательно, [S_2=dfrac{16cdot 4}5=12,8.]

Ответ: 12,8

Задание
7

#3047

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как (3:7). Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как (15:7).

Площадь боковой поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi Rl). Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как [dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2}] Так как радиус первого конуса относится к радиусу второго как (15:7), то есть (frac{R_1}{R_2}=frac{15}7), то [dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad
dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2.]

Ответ: 0,2

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Базовая информация

Объем геометрической фигуры — это количественная характеристика пространства, которое занимает тело. Она определяется его формой и размерами.
Чтобы задачи на вычисление объемов геометрических фигур не вызывали затруднений, рекомендуем освежить в памяти основные формулы.

• Объем куба равняется кубу длины его грани.

Для его расчета используется формула: V = a³, где V — объем куба,
a — длина его грани.

• Объем призмы равняется произведению площади основания фигуры на высоту.
  Чтобы его рассчитать, воспользуйтесь следующий формулой: V = S_o h, где V — объем призмы, So — площадь ее основания, h — ее высота.
• Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты.
  Формула для его расчета: V = a · b · h, где a — длина,
  b — ширина, h — высота.
• Объем пирамиды равняется трети от произведения площади ее основания на высоту.

Рассчитать его можно по формуле:

V =
1/3
S_o· h ,

где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.

• Объем цилиндра равняется произведению площади его основания на высоту.
  Формулы для его расчета:

V =

π R² h

V =

S_o h

Где V — объем цилиндра, So — площадь основания цилиндра, R — радиус цилиндра, h — высота цилиндра, π = 3.141592.

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Кайф или жесть? Новая шкала перевода баллов ЕГЭ 2022 по математике

11 августа 2022

В закладки

Обсудить

Жалоба

Разбор основных прототипов задач на нахождение площадей фигур: треугольник, параллелограмм, трапеция, ромб.

planimetria_ploschad_figur.pdf

Автор: Марсель Нуртдинов.

Источник: vk.com/marsel_tutor