Как найти площадь фигуры если она неровная

Как рассчитать площадь комнаты?

Простая комната прямоугольной или квадратной формы В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.

Видео

Площадь поверхности правильной шестиугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро ( displaystyle b).

( displaystyle {{S}_{полн. пов. }}=4{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})Как найти ( displaystyle {{S}_{OCH}})?

Шестиугольник ( displaystyle ABCDEF) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете площади поверхности правильной треугольной пирамиды, здесь используем найденную формулу.

( displaystyle {{S}_{ABCDEF}}=6cdot {{S}_{AOF}}=6cdot frac{{{a}^{2}}sqrt{3}}{4}=frac{3sqrt{3}{{a}^{2}}}{2})Ну, и площадь боковой грани мы уже искали аж два раза

Формула Пика

Существует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.

Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.

Сколько насчитали?

У меня получилось ( Г = 22) на границе и ( В = 32) внутри.

Ну а теперь сама формула:

Делим границу пополам, прибавляем внутренности и вычитаем 1:

( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.)

Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂

Площадь прямоугольника

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

S_ABCD = AB · BC S_ABCD = 3 · 7 = 21 см² Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны и две не параллельны.

S = 0,5 × (a + b) × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны под прямым углом.

Круг

Круг — это множество точек на плоскости, ограниченных окружностью, удаленных от центра на равном радиусу расстоянии. Радиусом принято называть отрезок, соединяющий центр с любой точкой окружности.

1. S = π × r², где r — это радиус, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

   

2. S = &pi × d² : 4;, где d — это диаметр.

   

3. S = L²​ : (4 × π), где L — это длина окружности.

   

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Навигация по записям

Предыдущая статьяЕсли диагонали то этот параллелограмм является прямоугольником – Признаки прямоугольника и квадрата — урок. Геометрия, 8 класс.

Следующая статья Площадь прямоугольника равняется произведению половины квадрата – Площадь прямоугольника равняется произведению половины квадрата

Теги

Как найти площадь геометрической фигуры по клеточкам?

Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.

---

Площадь фигуры по клеточкам

Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел — это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

N — количество узлов, которые находятся внутри фигуры.

M — количество узлов, которые находятся на границах (на вершинах и сторонах).

---

Примеры нахождения площади по клеточкам

1) Найдём площадь треугольника. Будем считать, что одна клетка — это 1 см.

Отметим внутренние узлы и узлы, которые находятся на границах.

N = 7 (внутренние).

M = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 — 1 = 10 см².

2) Найдём площадь трапеции по клеточкам, одна клетка — это 1 см. Отметим все узлы и подсчитаем их количество.

N = 11 (внутренние).

M = 12 (узлы на границах).

Площадь трапеции S = 11 + 12/2 — 1 = 16 см².

3) Найдём площадь произвольного многоугольника. Одна клетка — это 1 см.

Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.

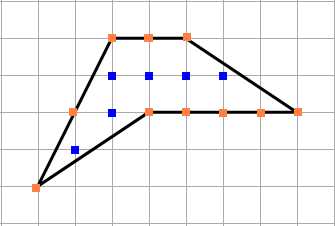
N = 6 (внутренние узлы).

M = 8 (узлы на границах).

Площадь многоугольника S = 6 + 10/2 — 1 = 10 см².

www.bolshoyvopros.ru

Вычисление площадей фигур, изображенных на клетчатой бумаге



При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?

Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.

Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.

Возможны следующие случаи.

1. Фигура представляет собой треугольник, параллелограмм, трапецию:

1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;

2) подставить найденные величины в формулу площади.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.

Рис. 1. Треугольник

Решение. Подсчитываем клеточки и находим: . По формуле получаем: .

2 Фигура представляет собой многоугольник

Если фигура представляет собой многоугольник то возможно использовать следующие методы.

Метод разбиения:

1) разбить многоугольник на треугольники, прямоугольники;

2) вычислить площади полученных фигур;

3) найти сумму всех площадей полученных фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.

Рис. 2. Многоугольник

Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.

Рис. 3. Многоугольник. Метод разбиения

Площади треугольников равны: , , , площадь прямоугольника — . Складывая площади всех фигур получим:

Метод дополнительного построения

1) достроить фигуру до прямоугольника

2) найти площади полученных дополнительных фигур и площадь самого прямоугольника

3) из площади прямоугольника вычесть площади всех «лишних» фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.

Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.

Рис. 4. Многоугольник. Метод дополнения

Площадь большого прямоугольника равна , прямоугольника, расположенного внутри — , площади «лишних» треугольников — , , тогда площадь искомой фигуры .

При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.

Формула Пика

Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.

Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

Например, для многоугольника, изображенного на рисунке 5.

Рис. 5. Узлы в формуле Пика

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.

Рис. 6. Многоугольник. Формула Пика

Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:

Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.

1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.

Рис. 7. Условие задачи 1

2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).

Рис. 8. Условие задачи 2

3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.

Рис. 9. Условие задачи 3

4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.

Рис. 10. Условие задачи 4

5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.

Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.

Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.

Литература:

1. Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
2. Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
3. Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.

yun.moluch.ru

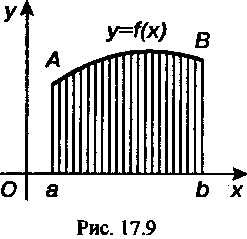
Площадь криволинейной трапеции, ограниченной сверху графиком функции, слева и справа — прямымиСоответственно,

Снизу — осью(рис. 17.9), вычисляется по формуле

(17.26)

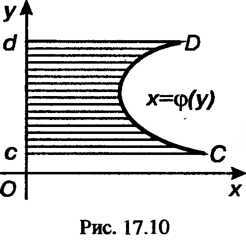
Площадь криволинейно трапеции(рис. 17.10), ограниченной справа

Графиком функции, сверху и снизу — соответственно прямыми

, слева — осью, определяется формулой

(17.27)

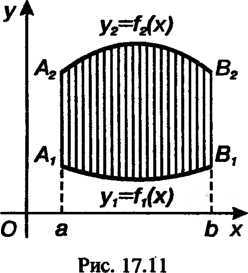
Площадь криволинейной фигуры, ограниченной сверху графиком

Функции, снизу — графиком функции, слева и справа —

Прямыми(рис. 17.11), вычисляется по формуле

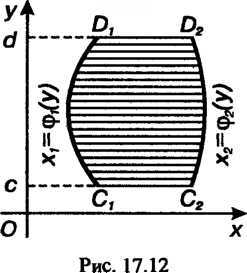
Площадь фигурыОграниченной слева и справа соответственно гра

Фиками функций, снизу и сверху — прямыми

(рис. 17.12), определяется формулой

(17.29)

Если линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениямиГде

То

(17.30)

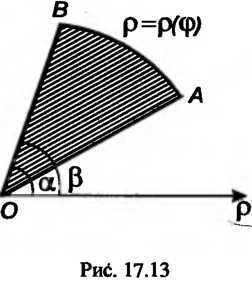
Площадь сектора(рис. 17.13), ограниченного дугой линии, заданной уравнением в полярных координатах, и двумя полярными радиусами

И, соответствующими значениям, определяется формулой

Пример 17.13. Найти площадь фигуры, ограниченной линиейИ осью

Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (рис. 17.14). Решая систему уравнений

Получаем

Следовательно,

По формуле (17.26) находим

Пример 17.14. Найти площадь фигуры, ограниченной линиейИ осью

Данная фигура представляет собой криволинейную трапецию, прилежащую к оси(см. рис. 17.15). Найдем точки пересечения линии с осью, для чего решим систему уравнений. Из этой системы получаем

; это означает, что в формуле (17.27), которой здесь необходимо пользоваться, нужно положить

Следовательно,

Пр имер 17.5, Вычислить площадь фигуры, ограниченной линиями

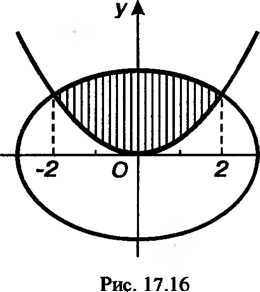
Данная фигура ограничена сверху дугой эллипсаСнизу — дугой пара

Болы(рис. 17.16).

Площадь вычислим по формуле (17.28).

Решая систему уравнений находим- абсциссы точек пе

Ресечения заданных линий; следовательно,

’ Каждое из уравнений разрешаем

Относительно

(В формуле (17.28) через обозначена функция, график которой ограничивает фигуру сверху.)

Таким образом, искомая площадь

Для вычисления первого интеграла применим подстановку, тогда

Поскольку

Пример 17.16. Вычислить площадь области, ограниченной эллипсом

В силу симметрии эллипса относительно координатных осей достаточно вычислить площадь части области, лежащей в первой четверти, и результат умножить на 4. Заметим, что в этом случаеМеняется от 0 доПоэтомуБудет меняться отДо 0. По формуле (17.30) находим

Замечание. В частном случае, когда, получаем-

Площадь круга радиуса

Пример 17.17. Вычислить площадь области, ограниченной лемнискатой

Принимая во внимание симметрию линии относительно ее оси (см. п. 2.10), по формуле (17.31) получаем

< Предыдущая		Следующая >

matica.org.ua

Расчет площади комнаты: способы, формулы, примеры

Процедура проведения ремонта в помещении требует обязательного расчета площади стен, потолка и пола. Так как во время покупки строительных материалов эти значения помогают не ошибиться в их количестве. О способах и примерах расчета площади помещения поговорим далее.

Оглавление:

1. Причины для проведения расчета площади комнаты
2. Площадь комнаты: проведение расчета площади пола
3. Определение площади прямоугольной комнаты и потолка
4. Какова площадь комнаты в которой имеются ниши и выступы
5. Как определить площадь комнаты с неровными стенами
6. Как высчитать площадь комнаты, в которой имеется многоуровневый потолок
7. Определение общей площади комнаты
8. Определение минимальной площади комнаты
9. Оптимальная площадь комнаты

Причины для проведения расчета площади комнаты

Существует большое количество причин, по которым определяется площадь стен, потолка или пола в помещении. В некоторых случаях, необходимы данные об общей площади комнаты. Предлагаем ознакомиться с наиболее часто встречающимися причинами определения площади комнаты или отдельных ее частей:

• если планируются работы по установке подвесных потолков, то необходимо определить общую площадь потолка, для определения количества материалов, используемых при проведении работ;

• при установке натяжных потолков, также нужно вычислить общую площадь потолка, чтобы предварительно спланировать материальные средства;
• для покраски или отделки потолка также следует знать его площадь, практически все лакокрасочные изделия и грунтовки имеют в технических характеристиках показатель расхода на один квадратный метр;
• отделка стен гипсокартоном требует вычисления общей площади стен, для покупки нужного количества материала;
• при найме строителей, например, для отделки пола плиткой, каждый метр квадратный имеет определенную стоимость, которая считается в конце выполнения работ;
• при продаже дома или при его оформлении, такой параметр как жилая площадь, площадь кухни и других комнат также является особо важным.

Площадь комнаты: проведение расчета площади пола

Для определения площади пола существуют разные причины: ремонт и покупка материалов для его отделки, проведение теплоизоляции, вычисление полезной площади и т.д.

Проще всего определить площадь помещения квадратной или прямоугольной формы. В таком случае, понадобится значение длины и ширины пола, которые умножаются друг на друга. Данный вариант не требует освобождения помещения от шкафов и прочей мебели. Достаточно просто измерить расстояние. Однако, при наличии камина в комнате, следует его площадь вычесть из общего полученного результата.

В принципе, все предметы, которые находятся на полу постоянно и не имеют возможности в перемещении, например, встраиваемые шкафы, вычисляются из общей площади пола.

Более сложным представляется расчет площади пола в помещении, которое имеет неправильную форму. Стандартные комнаты, конечно имеют форму прямоугольника или квадрата, хотя существуют помещения с разного рода нишами, углублениями, арками, выступами и т.д. Такой вариант подсчета площади пола более сложный, так как требует вычисления площади фигур, входящих в состав помещения по отдельности.

Для вычисления общей площади следует разбить пространство на несколько правильных фигур, в виде прямоугольников, трапеций, квадратов и т.д. Например, если помещение имеет г-образную форму, то достаточно его разделить на два прямоугольника, вычислить площадь каждого из них и суммировать полученные результаты.

Если помещение имеет г-образную форму, однако она проходит не под прямым углом, то кроме двух прямоугольников в нем еще присутствует треугольное пространство, площадь которого также вычисляется. Для вычисления площади треугольника достаточно один катет умножить на другой.

При наличии полукруглых фрагментов в виде цилиндрических или сегментных частиц, расчеты усложняются. Для расчета площади пола в такой комнате требуется также разделить пространство на несколько частей, площадь которых вычисляется по отдельности.

Бывают варианты помещений, которые имеют разные уровни пола, то есть возвышенности или уклоны. Таким образом, помещение разделяется на несколько зон. Например, в кухне выделяется столовая и рабочая части. То же самой и бывает с потолком, например, многоуровневым. Для вычисления площади пола с уступами или возвышенностями, следует опять же разделить пространство на части в виде прямоугольников или квадратов, а те самые выступы, измерить линейкой и вычислить их площадь. Таким способом получится провести расчет общей площади помещения.

Учтите, что в таком случае предпочтительно использовать рулетку, которая устанавливается вблизи основания. Кроме того, потребуется карандаш и тетрадь, для записывания всех значений. В итоге, покупка краски и определение количества отделочного материала для пола выполнится быстро.

Не выполняйте замеры по стене, так как она может быть кривой и приведет к возникновению неточности в процессе определения площади пола. Особой сложностью отличаются работы по определения площади пола, на котором имеются уступы в виде полукруга или волны. Данная ситуация предполагает измерение каждой из дуг, нахождение радиусов и раздробление площади на несколько геометрических фигур. С помощью определения площади для каждой из них вычисляется общая формула асимметричного сегмента.

Определение площади прямоугольной комнаты и потолка

Прямоугольное помещение является наиболее типичным и часто встречающимся вариантом. Для расчета площади достаточно длину помещения умножить на его ширину. Например, если длина комнаты составляет 3,40 м, а ее ширина 5,20 м, то для определения площади потолка достаточно 3,40х5,20, в итоге получится 17, 68 метров квадратных площади. Для расчета периметра потолка используется другая формула, которая подразумевает сумму удвоенных его длины и ширины. То есть, периметр потолка ровняется 2х3,40+2х5,20=17,2 м.

Поэтому, в процессе закупки профилей, потребуется 17,2 метра материала. Однако, рекомендуется, даже при проведении точнейших расчетов, покупать материал с запасом в 10-15 процентов, для компенсации различного рода механических повреждений и стыков.

Какова площадь комнаты в которой имеются ниши и выступы

Для определения площади такого помещения следует изрядно потрудиться и выполнить такие действия:

1. Сделайте проект комнаты с учетом всех конструктивных особенностей.

2. Измерьте и обозначьте значения высоты и длины по всем ровным стенам.

3. С помощью линейки и угольника разделите пространство на несколько зон, в виде правильных фигур.

4. Каждую из сторон фигуры следует измерить и обозначить в проекте.

5. Согласно формуле для расчета площади фигуры определите значения каждой из них и суммируйте полученные результаты.

Как определить площадь комнаты с неровными стенами

При наличии помещения, в котором стены имеют вид многогранников или непрямых непропорциональных фигур, расчеты проводить гораздо сложнее. Измерить периметр в таком помещении достаточно просто. Следует использовать рулетку и пройти с ней по всей комнате, измеряя каждый из участков по отдельности.

Площадь комнаты определяется путем проведения зарисовок и проектирования помещения. После того как эскиз готов, разбиваем пространство таким образом, чтобы получить максимальное количество пропорциональных фигур в виде квадрата, треугольника или прямоугольника.

Для того, чтобы определить площадь сегмента, который имеет форму прямоугольника с одинаковыми ребрами, достаточно измерить величину катетов, которые умножаются между собой и разделяются пополам. То есть, для определения площади треугольного сегмента с катетами 0,5 и 0,9 м следует провести такие расчеты:

0,5х0,9/2= 0,225 метра квадратных.

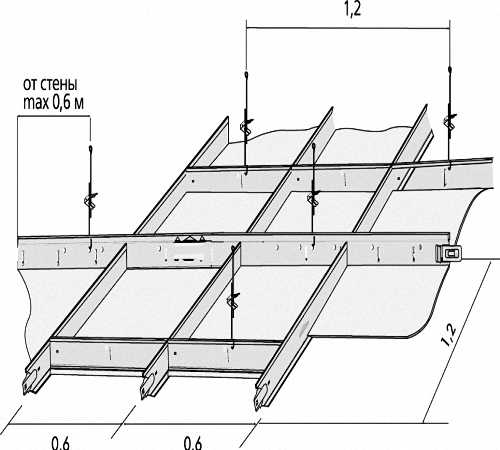
Как высчитать площадь комнаты, в которой имеется многоуровневый потолок

Потолок, на котором имеются уступы рассчитать сложнее, однако вполне реально. Существуют многоярусные потолки, которые имеют форму прямых линий их расчет проводить легко, но бывают такие конструкции, которые требуют особой внимательности, так как они состоят из дуго- или волнообразных фрагментов для расчета которых требуется приложить особые усилия.

Рассчитывать каждый из участков слишком долго и затратно, тем более, что в итоге получится не всегда правильный результат. Ведь, дуги, сконструированные на потолке могут быть произвольными.

Проще всего определить площадь комнаты по общей площади пола. Для этого, следует выполнить ряд действий:

1. Измерьте все прямые участки стен.

Предпочтительно проводить замеры поближе к потолку, так как длина стены сверху и снизу помещения может отличаться.

2. Определите площадь пола по ранее указанным способам.

3. На каждом из вертикальных участков измерьте их высоту и длину и умножьте эти показатели.

4. Прибавьте их к общему значению площади пола.

Определение общей площади комнаты

Для того, чтобы ответить на вопрос как узнать площадь комнаты в квадратных метрах, предлагаем ознакомиться с инструкцией, которая поможет выполнить эту задачу:

1. Позаботьтесь об очищении пространства возле стен.

Стены комнаты должны быть в свободном доступе. Таким образом, повысится правильность и точность измерения. При возможности лучше освободить помещение целиком, так как в проведении определенных расчетов потребуется измерять и центральные участки.

2. Определите в помещении участки, имеющие правильную форму.

Если помещение имеет вид прямоугольника, то в делении оно не нуждается. В противном случае, комната разделяется на фигуры в виде квадратов, полукругов, трапеций, треугольников или прямоугольников.

3. Сделайте эскиз помещения, так работать станет легче.

Измерение площади комнаты нужно выполнять по эскизу, на котором отмечаются все замеры. Совет: При отсутствии бумаги и при необходимости проведения срочного замера, используйте клейкую ленту, которая крепится на каждую стену.

4. Длина и ширина комнаты, площадь.

Каждая стена должна быть измерена по ширине и длине желательно дважды. Для того, чтобы не измерять всю стену целиком, ее нужно разбить на несколько фрагментов, а в итоге, полученные результаты суммировать.

Для того, чтобы убедиться в правильности проведения расчета, при наличии свободного времени, замеры проводятся дважды.

5. Определите площадь каждого из участков:

• площадь прямоугольника ровняется умножению его длины на ширину;
• площадь квадрата, это одна из его сторон в квадрате;
• площадь треугольника — высота и сторона, умножаются между собой и полученное значение разделяется на два;
• площадь круга число Пи умножается на радиус в квадрате.

6. Площади ранее определенных участков складываются между собой.

Определение минимальной площади комнаты

1. Участки в виде прямоугольника.

С помощью рулетки измеряется длина и ширина участка, они умножаются между собой. Данные чаще всего округляют до сантиметров.

2. Треугольник.

Площадь данного участка определяется путем умножения одной стороны треугольника на его высоту, то есть линию, опущенную с вершины треугольника, которая разделяет его на две равных части. Полученное значение удваивается.

3. Окружность или полуокружность.

Определение радиуса. Данное значение переводится в квадрат, умножается на число Пи. При наличии полукруга, значение разделяется на два.

Кроме того, в интернете существуют специальные онлайн калькуляторы, позволяющие провести все расчеты быстро и качественно. Для работы с ними достаточно выбрать форму участка комнаты, измерить его с помощью рулетки и ввести данные. Программа сама проведет все необходимые расчеты и определит площадь.

Оптимальная площадь комнаты

Каждая комната имеет свой размер, и во время планировки дома, этот фактор учитывается в соответствии с их назначением. Минимальное значение площади обычной жилой комнаты составляет восемь метров квадратных.

Площадь общей комнаты или гостиной должна составлять от 13 до 23 метров квадратных. Спальня должна располагаться в углу дома, и быть не проходным помещением.

Минимальная высота жилого помещения — 240 см. Не рекомендуется обустраивать комнаты с высотой более 300 см, так как они совсем непрактичны, для их обогрева в зимнее время потребуется большое количество материальных вложений.

Каждая комната должна отличаться наличием естественного освещения. Минимум 30 % всех стен должны приходиться на окна. Учтите, что предпочтительнее устанавливать окна на южной стороне, так как зимой, на северной стороне, они будут провоцировать большие теплопотери.

Если жилая площадь дома или квартиры составляет от 15 до 55 метров квадратных, то минимальная площадь кухни должны быть 6 метров квадратных. При планировке кухни в зданиях с жилой площадью более 55 квадратных метров, кухня должна занимать минимум пятую часть всего дома.

Если кухня занимает более 10 квадратных метров, возможен вариант ее использования в качестве столовой или комнаты для приема гостей. Минимальная ширина прихожей составляет 140 см, в ней также должно присутствовать естественное освещение.

Для детской комнаты достаточно площади в 10-15 метров квадратных. Самыми маленькими должны быть ванная и туалет. Их площадь ровняется 4-8 квадратным метрам.

strport.ru

Площадь сложных фигур — Памятки по математике — Памятки ученикам

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

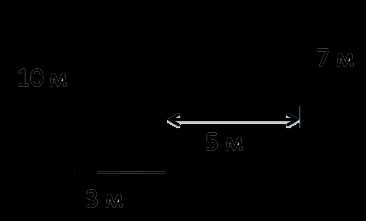
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

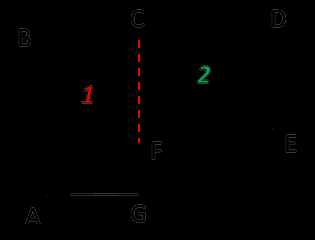S_ABCE = AB • BC
S_EFKL = 10 • 3 = 30 м²
S_CDEF = FC • CD
S_CDEF = 7 • 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.

S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

---

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD.

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB • BC
S_ABCD = 5 • 4 = 20 см²

S _ABC = S_ABCD : 2 

S _ABC = 20 : 2 = 10 см²

S _ABC = S _ACD = 10 см².

www.mamapapa-arh.ru