Тема: Площадь фигуры
Цель урока: познакомить детей с новым понятием
«площадь фигуры»
Задачи:
1. Дать представление о площади фигур.
2. Познакомить с различными способами сравнения
площади фигур: «на глаз», путём наложения одной фигуры на другую, с использованием
одинаковых мерок.
3. Развивать логическое мышление, память, интерес к
предмету.
4. Воспитывать чувство дружбы, взаимовыручки, умение
слушать друг друга.
Умения
Предметные: знать, что такое площадь фигуры,
уметь отличать понятия «площадь» и «периметр»
Метапредметные:
– Регулятивные: уметь формулировать тему и цель
урока, уметь находить и исправлять свои ошибки.
– Познавательные: совершенствование навыков
устных вычислений, выбор наиболее эффективных способов решения поставленной
задачи, самостоятельное создание алгоритмов деятельности.
– Коммуникативные: формирование конструктивных способов взаимодействия в
группе и в парах.
– Личностные: проявлять внимательность и
оказывать в случае необходимости помощь соседу по парте.
Ход
урока
1.Организационный момент
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.
2. Актуализация знаний.
Математика нас ждёт! Начинаем устный счёт.
3.Устный счёт
Увеличьте каждое число на 4 десятка.
24 45 18 32 51
44 39 59
Уменьшите эти числа на 4 единицы
12 34 45 53 67 78
92
Задача
Купили 4 грозди бананов, по 7 штук в
каждой, и ещё одну гроздь, в которой было 12 бананов. Сколько бананов купили?
4.Итог устного счёта.
5. Постановка цели урока.
– Ребята, посмотрите на доску. В таблице зашифровано
слово. Чтобы мы смогли отправиться дальше, нам необходимо это слово
расшифровать. Для этого мы должны решить числовые выражения и расставить в
таблицу буквы соответственно ответам
70,42,30,16,36,26,54
9*4(а)
55+15(п)
40-14(д)
8*2(щ)
(7+2)*6(ь)
6*5(о)
(5+1)*7(л)
– Какое слово у вас получилось?(Площадь)
– Сформулируйте тему нашего урока.
– Как вы думаете, что мы узнаем на сегодняшнем уроке?
Откройте тетради, запишите число, кл.
работа.
5. «Открытие» нового знания.
1) Подготовка
– Ещё в далёкие исторические времена человеку
приходилось постепенно постигать не только искусство счёта, но и измерений. С
развитием науки, техники у людей возникла острая потребность измерять расстояния,
объём, массу, время, а затем и площадь. У каждого народа были свои
единицы измерения. Например, на Руси в древности для измерения длины
пользовались теми мерками, которые всегда были при себе: пальцы, локти,
ступни.
– Давайте попробуем измерить ширину парт ладонями
(учитель демонстрирует на доске)
– Сколько ладоней составляет ширина парт? (слушает
ответы нескольких учеников) Почему получились разные ответы?
– Мы не смогли дать однозначный ответ на вопрос. У нас
возникла проблема. Так и в далёкие времена возникали споры. Послушайте
задачу:
2 купца мерили длину одинакового отреза ткани локтями.
Один отмерил 29 локтей, другой – 30 (Учитель демонстрирует с помощью шарфа, как
купцы отмеряли длину отреза ткани, затем вызывает ученика, который повторяет
действия учителя и оба называют получившиеся значения)
– Почему получился разный результат?
– К какому выводу пришли люди?
– Со временем люди поняли это, поэтому сейчас во всём
мире используют более точные общие для всех стран единицы измерения. Какие
линейные единицы измерения длины вы уже знаете?
– Ребята, наши предки научились измерять длину одной
из первых и с введением единиц измерения этой величины споров больше не
возникало. Тогда наши предки столкнулись с другой проблемой: как измерить
площадь земель (земельных наделов). Долго люди не могли понять, как же
измерить площадь, какие выбрать мерки.
2) Изучение нового материала
– Посмотрите на доску и назовите фигуры, которые вы на
ней видите(…)
– Посмотрите, я беру квадрат и провожу указкой по его
поверхности. Эту внутреннюю область фигуры называют площадью (таким
образом учитель демонстрирует площади всех фигур на доске).
– Ребята, у вас на партах лежат такие же наборы из
геометрических фигур. Покажите по очереди друг другу рукой площади этих фигур.
– Молодцы! А теперь давайте покажем площади различных
предметов в окружающей обстановке класса. (Учитель поочерёдно вызывает ребят
показать площади поверхности учебника, тетради, доски).
-Ребята! Обратите внимание, что площадь и периметр –
это разные величины! Что такое периметр?
А площадь – это внутренняя часть
фигуры, ограниченная ломаной линией.
3) Практическая работа.
– Теперь мы знаем, что такое площадь, значит, мы можем
научиться её измерять. Из вашего набора возьмите самую большую и самую
маленькую на ваш взгляд фигуры. И покажите мне. Почему вы так решили?
– Как вы думаете, когда мы говорим о величине фигуры
(большая, маленькая), что мы у них сравниваем?
– Верно, площадь характеризует больше или меньше места
фигура занимает на плоскости.
– Попробуйте найти одинаковые по площади фигуры.
Почему вы так решили?
Таким же образом учитель предлагает сравнить площади
других фигур.
– А теперь посмотрите на доску. (учитель демонстрирует
на интерактивной доске 3 участка прямоугольной формы разного цвета и размера,
состоящие из разного количества мерок).
– Какой формы эти участки?
– На сколько мерок разбит 1 участок?…
Учитель предлагает сравнить площадь фигур по найденному
числу мерок и наложением.
– Почему же так получилось?
– Ребята, для измерения площади фигур нельзя брать
какие угодно мерки. Иначе при измерении площади одной и той же фигуры будут
получаться разные числа. К такому выводу пришли учёные Ньютон и Лейбниц и
решили обозначать площадь буквой S.
Первая мерка, с которой мы подробно будем знакомиться ,
называется квадратный сантиметр. (демонстрируется мерка 1 см2)
– Что представляет собой эта мерка?
Обозначается эта мерка см2. Начертите у
себя в тетради такую же мерку и обозначьте её.
– Что можно измерить с помощью квадратных сантиметров?
5. Первичное закрепление.
с.41 №32,с.50 №27,с.51№33
6.Подведение итогов урока.
– Ребята, что нового вы сегодня узнала на уроке?
– Что вызвало затруднения?
– Что показалось наиболее интересным?
7. Рефлексия.
8. Домашнее задание.
Урок математики в 3-м классе по теме: “Площадь. Единицы площади”
Цели урока:
1. Дать представление о площади фигур, познакомить с различными способами сравнения фигур: “на глаз”, путём наложения одной фигуры на другую, с использованием различных единиц измерения площадей.
2. Закрепить знание свойств геометрических фигур.
3. Закрепить умение точно производить измерения и чертить квадрат и прямоугольник.
4. Закрепить знание изученных таблиц умножения и соответствующих случаев деления.
5. Закреплять умение решать задачи
6. Развивать логическое мышление и пространственное воображение.
7. Воспитывать аккуратность при выполнении работы.
Оборудование. Для учащихся: учебник математики для 3 класса Моро, рабочая тетрадь, линейка, простой карандаш, цветные карандаши, рабочая тетрадь, листы с заданиями: с фигурами наложения, с фигурами п.7, геометрические фигуры: квадраты зелёный 6х6 см, белый 4х4 см, круги жёлтый и красный диаметром 5 см, прямоугольник 5х3.
Для учителя: образец написания цифр, геометрические фигуры: квадраты зелёный 6х6 см, белый 4х4 см, круги жёлтый и красный диаметром 5 см, прямоугольник 5х3, листы с заданиями: с фигурами наложения, с фигурами п.7(3) образец и заполненный, на доске 3(а), 3(б), 3(в), 4.
ХОД УРОКА
I. Оргмомент.
Начинаем наш урок.
Надеюсь, он пойдёт вам впрок.
Постарайтесь всё понять,
Ответы полные давать.
II. Запись в тетради числа и слов “Классная работа”.
III. Устный счёт и чистописание.
а) Найдите в каждом ряду числа, которые не являются результатом табличного умножения.
6 18 17 12 41
24 30 16 11 28
7 36 27 35 71
Запишите числа 17, 41, 11, 7, 71. Обратите внимание на образцы написания цифр.
Докажите, что оставшиеся числа являются результатом табличного умножения.
б) Из данных чисел выбери пары, произведения и частные которых равны 6.
1 4 6 2 54 12 3 36 7 8 24 18 42 48 9
в) Сторона квадрата 2 см. Чему равен периметр? Найди правильное решение.
2+2+2+2=8(см)
2+4=6(см)
4+4+4+4=16(см)
2 • 4=8(см)
4 • 2=8(см)
г) Укажите, какой фигуре соответствует каждый из указанных признаков:
- 4 стороны равны; (квадрат)
- имеет три угла; (треугольник)
- состоит из 4 отрезков; (четырёхугольник)
- все углы прямые; (прямоугольник)
Дайте общее название фигурам – (геометрические).
IV. Сообщение темы урока.
Знание таблиц умножения и соответствующих случаев деления, свойств геометрических фигур понадобится нам при изучении темы нашего урока. Решив примеры на порядок действий и каждому ответу подставить букву, составить слово и узнать тему урока.
24+56:8·3=(45) А 7·7-9=(40) П (57-22):7+63=(68) Ь 56:7+16=(24) О
36:6·4-(23-17)=(18) Л (80-45):5=(7) Д 5·9-(6+14:2)=(32)Щ
П Л О Щ А Д Ь
40 18 24 32 45 7 68
Итак: тема нашего урока: Площадь. Единицы площади. Записать на доске слово ПЛОЩАДЬ.
Сегодня мы выясним, что такое площадь фигуры и как можно сравнить площади фигур.
V. Работа по теме урока.
1. Словарная работа.
Назовите орфограммы в слове “ Площадь”.
– Гласная после шипящих: сочетание ча-ща пиши с буквой а;
– Смягчающий мягкий знак, смягчает предшествующий согласный звук, а сам звука не даёт.
2. Работа с геометрическим материалом.
а) Возьмите зелёный и белый квадраты. Покажите квадрат, который больше.
Как сравнивали?
Видно “ на глаз”.
Про такие фигуры говорят, что площадь зелёного квадрата больше площади белого квадрата.
Как ещё можно сравнить площади этих фигур?
Можно наложить одну на другую.
Наложите и сравните площади квадратов.
Белый квадрат полностью вместился в зелёном, значит площадь зелёного квадрата больше площади белого квадрата.
б) Возьмите жёлтый и красный круги. Сравните площади и покажите круг, площадь которого меньше.
Площади кругов равны, так как при наложении круги полностью совпали.
Что же такое площадь фигуры? Как вы думаете?
Если правильного ответа не будет, учитель сообщает:
Площадь-это место, которое занимает фигура на плоскости.
Как мы сравнивали площади фигур?
“На глаз” и наложением друг на друга.
Физкультминутка. Можно аудио
Встаньте дружно из-за парт
И скорее стройтесь в ряд!
Повернитесь вправо, влево,
Наконец, присядьте смело!
Поработаем ногами,
Раз, два, три!
Поработаем руками!
Раз, два, три!
Улыбнёмся: день хороший,
И похлопаем в ладоши.
3. Продолжение работы с геометрическим материалом.
Единицы площади.
а) Возьмите фиолетовый прямоугольник и белый квадрат.
Как удобнее сравнивать площади прямоугольника и квадрата “на глаз” или наложением?
Дети пытаются сравнить площади фигур “на глаз” и наложением.
“На глаз” или наложением сравнить площади прямоугольника и квадрата нельзя, фигуры разные по форме и ни одна полностью не вмещается в другой.
Как же сравнить площади этих фигур?
Ответы детей.
Если правильного ответа не будет, учитель сам предлагает начертить прямоугольник и квадрат в тетради.
а) Назовите общие свойства прямоугольника и квадрата.
Чем отличаются?
б). Вычерчивание прямоугольника и квадрата в тетради.
Измерьте сторону квадрата.
4 см
Начертите квадрат. Укажите на чертеже длину стороны квадрата.
Измерьте длину и ширинку прямоугольника.
5 см, 3 см
Начертите прямоугольник. Укажите длины сторон прямоугольника.
Как же сравнить площади этих фигур?
Ответы детей.
1. Если правильного ответа не будет, обратить внимание детей на то, что, начертив фигуры в тетради, мы разбили их на одинаковые фигуры меньшего размера – клетки тетради.
Можно посчитать клетки.
Посчитайте клетки, I вариант – квадрата, II вариант – прямоугольника. Сколько клеток поместилось в квадрате, в прямоугольнике? Запишите числа и сравните их.
64>60
Сравните площади квадрата и прямоугольника.
Площадь квадрата больше площади прямоугольника.
Большую площадь имеет та фигура, которая содержит большее число клеток.
2. Но площадь фигур можно измерить и другими мерками. Можно разбить фигуру на одинаковые треугольники или большие квадраты.
Демонстрация прямоугольника разбитого на одинаковые треугольники.
3. Разобьём квадрат и прямоугольник на квадраты со стороной 1см. Подсчитайте, сколько квадратов со стороной 1см поместилось в квадрате? В прямоугольнике? Запишите числа и сравните их.
16>15
Сравните площади фигур.
Площадь квадрата больше площади прямоугольника.
Результат сравнения площадей не зависит от выбора единиц измерения.
4. Как удобнее подсчитать квадраты, на которые разбит прямоугольник?
3 ряда по 5 квадратов, 5 • 3 = 15
5 столбцов по 3 квадрата, 3 • 5 = 15
5. Подведём итог наших наблюдений.
Что же такое площадь фигуры? Площадь-это место, которое занимает фигура на плоскости.
Если обозначить стороны буквами а и b, то при вычислении получаем формулу S=a·b
Как можно сравнить площади фигур? “На глаз” и наложением друг на друга.
Как можно вычислить площадь фигуры? Используя формулу.
Физкультминутка. Можно использовать аудио
Как же долго мы сидели,
Наши руки онемели,
Наши ноги затекли,
Ими топнем: раз, два, три!
Руки в стороны, дружок,
Раз, два, три, потом – прыжок.
Со здоровьем всё в порядке,
Если делаешь зарядку.
VI.Работа над пройденным материалом.
Учебник математики 3 класс Моро, Бантова и др. 2014 год.
Страница 57, №4.
– От доски длиной 8 метров отпилили часть длиной 2 метра. Во сколько раз больше оставшаяся часть, чем отпиленная?
– О чём говорится в задаче? (О доске от которой отпилили часть.)
– Что нужно узнать в задаче? (Во сколько раз больше оставшаяся часть, чем отпиленная?)
– Что необходимо знать, чтобы сравнить? (Сколько отпилили т сколько осталось).
– Запишем задачу кратко.
Было – 8 м
Отпилили – 2 м Во ? раз больше
Осталось – ? м
1) 8-2=6 (м) – осталось
2) 6:2=3 (раза)
Ответ: в 3 раза больше оставшаяся часть, чем отпиленная.
VII. Закрепление.
1) учебник с.57 № 1 (устно).
На рисунке изображены фигуры, которые при наложении не совпадут. Докажите, что их площади равны.
2. Раздели на три фигуры одинаковые по площади, и раскрась разными карандашами.
Построй фигуру равную по площади данной, но другой формы.
3. Задание на развитие пространственного воображения.
Раскрась фигуру. Существует два варианта: а) прямоугольник сверху, а квадрат снизу, б) прямоугольник снизу, а квадрат сверху. Выберите любой вариант.
VIII. Итог урока.
Завершаем наш урок.
Надеюсь, он пойдёт вам впрок.
Какую тайну мы сегодня открыли?
(Каждая фигура имеет площадь)
– Оценки за урок.
XI. Домашнее задание с пояснением.
Страница 57 №2 (3 и 4 столбики по действиям), №5.
Математика, 3 класс
Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр
Перечень вопросов, рассматриваемых в теме:
– что такое площадь фигуры?
– какие есть способы сравнения фигур по площади?
– что такое квадратный сантиметр?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
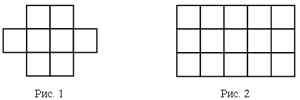
Сравним фигуры и расставим их в порядке убывания их площади.







Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.
В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».
Сравним фигуры и выясним, площадь какой фигуры больше.

Способом сравнения на глаз, определить площадь какой фигуры невозможно.
Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.
Сравним две фигуры.

Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.
Посчитаем количество мерок в фигурах: в синей фигуре содержится 6 мерок, в красной-5 мерок, следовательно, площадь синей фигуры больше площади красной, т. к. в синей фигуре 6 мерок-квадратов, а в красной – 5.
В математике мерка- квадрат. А квадрат со стороной 1 см называется квадратный сантиметр и обозначается см2..
Задания тренировочного модуля:
1.Выберите правильное высказывание:
Площадь фигуры – это…..
1. сумма длин всех сторон
2. внутренняя часть фигуры
Правильный ответ:
2. внутренняя часть фигуры
2. Выделите фигуры с одинаковой площадью.

Правильный ответ:

Цель: познакомиться с понятием площадь
фигуры.
Оборудование: презентация, модели:
квадратные сантиметры, квадратные дециметры,
квадратные метры.
| Этапы урока | Деятельность учителя | Деятельность учащихся |
| I. Мотивирование к учебной деятельности. 1. Организационный момент. |
Здравствуй, мой любимый класс, Очень рада видеть вас! Ты готов начать урок? Всё ль на месте? Всё ль в порядке? Ручки, книжки и тетрадки? |
Приветствуют учителя.
Проверяют свою |
| II. Актуализация знаний.
Устный |
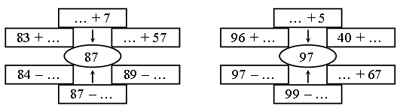
1)Вставьте пропущенные числа.
2) Решите задачу. В аллее 28 каштанов, а ясеней в 4 раза меньше. |
Повторяют правила нахождения неизвестных компонентов сложения и вычитания, закрепляют таблицу умножения. |
| III. Определение темы урока.
1. 2. Постановка проблемы. |
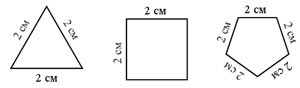
– Как называются данные на доске фигуры?
– Что их объединяет? (Это многоугольники,
– Как найти периметр каждого многоугольника? 2 + 2 + 2 = 6 (см) 2 + 2 +2 + 2 = 8 (см). 2 + 2 + 2 + 2 + 2 = 10 (см). – Как найти площадь этих фигур? – Какие трудности у вас возникли? – Сегодня на уроке мы узнаем, что называют |
Фиксируют затруднение. |
| IV. Открытие нового знания. | Какая фигура меньше занимает места на плоскости? Говорят, что треугольник имеет – Площадь какой фигуры больше? Площадь – свойство фигуры, занимать место на Площадь – это внутренняя часть фигуры. – Площадь квадрата больше, чем площадь круга? – Площадь какой фигуры больше красной или – Сможем ли мы сравнить площади фигур – Наложить мы не сможем эти фигуры, но можем Площадь фигуры можно измерять и другими Сравните жёлтый и красный прямоугольники по – Сколько квадратов в первом прямоугольнике, во – Почему так получилось? Чтобы этого не было вводятся специальные |
Работают с презентацией.
Треугольник Площадь четырёхугольника больше, чем площадь Площадь квадрата больше, чем площадь круга. Площадь двух кругов одинаковая. Сравнивают прямоугольники по количеству Т.к. фигуры разбиты на квадраты разных размеров. |
| V. Первичное закрепление.
Работа |
– Образуйте фигуры, площадь которой 3 кв. см.(5,4 кв.см) Назовите площадь. Фигуры у всех -Образуйте фигуры, площадь которой 5 кв. см. (4 Чтение правила по учебнику стр. 27.
(Квадратным сантиметром называют площадь
– Сформулируйте определение квадратного – Квадратный сантиметр, квадратный дециметр, Их обозначают так: см2, дм2, м2. – Рассмотрите вырезанные из бумаги квадраты – Сравните попарно площади этих квадратов. – В квадрате площадью 1 дм2 может |
Работают в парах. У учащихся модели У наших фигур одинаковые площади. Читают определение квадратного дециметра, Сравнивают попарно площади этих квадратов, |
| Физминутка. | Определите площади фигур на экране.
1) Площадь одного такого квадрата называют квадратным 2) Прямоугольник на рисунке состоит из 3 полос, |
1) Фигура состоит из 8 квадратов со стороной 1 см каждый. Значит, площадь всей фигуры равна 8 см2. 2) Весь прямоугольник состоит из 5 * 3 = 15 таких |
| VI. Самостоятель ная работа. Работа в группах. |
Дополни высказывание.
|
Работают в группах. Дополняют высказывание. |
| VIII. Систематизация и повторение. | Задание № 3 (с. 28).
Работа в печатной
Задание № 3,стр.13.
Напиши площадь данных фигур. |
Читают величины, записанные единицами площади. Устанавливают взаимосвязь между Записывают площадь фигур. |
| VII. Итог урока. | Выбери правильное утверждение:
1. 2. Площадь – это … – Назовите единицы измерения площади фигуры. Пригодится ли вам в жизни умение находить – Где и зачем? |
Выбирают правильное утверждение. |
| Рефлексия деятельности. | Покажите своё настроение в конце урока смайликом. – Что не получилось? Почему? |
Литература.
этапы
содержание
примечание
Орг.момент
Минутка чисто
писания
864
Охарактеризуйте число.
Сколько в нем сотен, десятков, единиц.
Назовите последующее и предыдущее число
Разложите на сумму разрядных слагаемых
Какое еще число можно получить из этих цифр
Пропишите число до конца строки
Записано на доске
Матем.
диктант
36:6, 45:5, 24:6, 21*1, 7*1, 6:6, 42:6, 6*5, 6*0, 5*8
Взаимопроверка ручеек.
Встали, перешли, проверили.
Встали, сели на места.
Поднимите руку, кто получил +
Какие правила мы знаем при умножении числа на 0?
При умножении числа на 1?
1 ученик у доски
Устный счет
Послушайте внимательно задачу.
В первой корзине было 18 яблок, а во второй на 3 яблока меньше. Сколько яблок во второй корзине?
О чем говорится в задаче?
Что известно?
Что нужно найти?
Что значит на 3 меньше?
Какие слова возьмем для краткой записи?
Составляем условие
1к-18яб
2к-? на 3яб.меньше.
Каким действием будем решать задачу (-) почему?
18-3=15яблок
Правильно!
Измените вопрос задачи так, чтобы она решалась в два действия
Найдите сколько всего яблок в двух корзинах?
18+ (18-3)=33 яблока
Решаем следующую задачу
1к-18яб
2к-? в 3р меньше
Что значит в 3р меньше?
Каким действием будем решать задачу? (:)
18:3=6яблок
Измените вопрос задачи так, чтобы она решалась двумя действиями
18 –(18:3) = 24яблока
На доске формула на 3 меньше
В 3р меньше
Подготовка к восприятию
Какие единицы измерения длины вы знаете?
Какая самая маленькая, самая большая?
Расскажи в парах единицы измерения длины
Кто рассказал поставьте +
Выполняем задание.
Впишите единицы измерения длины, чтобы равенство получилось верным.
-
= 10
1 = 10
Единицы измерения длины вы знаете, сегодня на уроке мы познакомимся с единицей измерения площади.
Формулы на доске
Объяснение нового материала
физминутка
Посмотрите на доску, какие фигуры вы видите? Какая фигура занимает меньше места на доске? Как вы определили?
На круг наложим квадрат. Что вы заметили? (квадрат поместился внутри круга)
Что мы можем сказать, площадь какой фигуры меньше, почему?
Сделаем вывод, площадь той фигуры меньше….
которая при наложении помещается в другой фигуре.
Площадь обозначается буквой S
Для того чтобы записать площадь фигуры нужно знать единицу измерения площади.
Единица измерения площади – квадратный сантиметр.
Что значит квадратный сантиметр
Это квадрат со стороной 1см.
Начертите в тетради квадрат со стороной квадратный сантиметр.
Для того чтобы узнать площадь фигуры нужно посчитать сколько квадратных сантиметров она в себя включает.
 Как живешь? Как идешь? Как бежишь?
Как живешь? Как идешь? Как бежишь?
Ночью спишь? Как берешь? Как даешь? Вот так
Как грозишь? Как шалишь?
Работа по учебнику
Подведение итогов.
д/з
Откройте учебник на стр 129 (1) посмотрите на первую фигуру. Какая это фигура?
Как мы узнаем площадь этой фигуры? (посчитаем количество квадратных см.)
S = 10см²
Посмотрите на вторую фигуру. Как узнаем площадь фигуры?
S = 9см²
Ребята? Площадь фигуры можно измерять с помощью палетки
Палетка – прозрачная пленка, расчерченная на квадратные см.
Чтобы измерить площадь с помощью палетки нужно положить палетку на фигуру и посчитать количество квадратных см.
На партах у вас лежит палетка и фигуры.
Измерьте площадь фигуры.
Так как мы измеряем площадь при помощи палетки?
Откройте учебник на стр 129 №4
Какая первая фигура? (круг)
Почитайте кол-во полных квадратов. – 6
Посчитайте кол-во неполных квадратов – 10
Если количество неполных квадратов 10, как мы узнаем сколько будет полных квадратов.(:2)
Теперь складываем кол-во полных и неполных квадратов
S = a + b2
На партах у вас лежат фигуры по алгоритму найдите площадь фигуры.
Расскажите формулу в парах.
Кто рассказал поставьте +
Откройте учебник на стр 131 №7.Решаем задачу.
Прочитайте задачу.
Читай ______!
О чем говорится задаче?
Что нам известно?
Что нужно найти?
Можем мы сразу ответить на вопрос задачи? Почему?
1.Сколько наборов цветных карандашей взял учитель?
2.По сколько штук в каждом стакане?
3.Сколько простых карандашей взял?
4. По сколько в каждом стакане?
5. Что значит разложил все карандаши в 7 стаканов?
6.Зная сколько всего карандашей и сколько стаканов мы сможем узнать сколько карандашей в каждом стакане?
Записываем условие задачи.
Вспомним. Что значит на 10 больше?
Каким действием мы найдем, сколько всего цветных карандашей? Почему?
Каким действием мы найдем сколько всего простых карандашей? Почему?
Как мы узнаем сколько всего карандашей?
Каким действием мы узнаем сколько карандашей в каждом стакане?
Запишем алгоритм на доске
-
*
-
+
-
+
-
:
За доску 2 человека. Остальные самостоятельно в тетради.
Взаимопроверка ручеек.
Кто получил + поднимите руку.
Выполняем упр.4 на стр 130
Вспомним, порядок выполнения действий
-
примера коллективно решаем.
-
примера по вариантам, 2 ученика за доской.
Взаимопроверка. Обменяйтесь тетрадями,проверили, оценили.
Кто получил + поднимите руку.
С какой единицей измерения мы познакомились? (кв.см)
Что значит кв.см.
Как мы находим площадь фигуры?
Как измерить площадь фигуры с помощью палетки?
Откройте дневники запишите д/з – стр 131 №8 (2)
№ 9 (2)
На партах палетка
И фигура
На лоске памятка
Алгоритм записан на доске
Записано на лоске