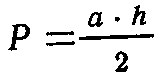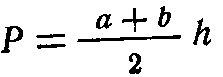Как найти площадь фигуры на карте - Сайт, где вы сможете решить свои вопросы

плотин, либо других гидротехнических сооружений, представляющих собой препятствие для свободного тока воды.

Для построения зоны затопления исходной величиной является абсолютная высота плотины или подпорного сооружения, а также положение самой плотины 1-2 на местности. Абсолютная высота плотины задает абсолютную высоту горизонтали (рис. 2.27), которую сравнительно легко провести между горизонталями, имеющимися на карте.

Граница зоны затопления показывает на карте местность, покрывающуюся водой после строительства плотины, что необходимо для принятия соответствующих предупредительных мер. Кроме того, использование горизонталей карты и отметки водного зеркала позволяет решить задачу о емкости водохранилища.

Существует несколько способов определения площадей: аналитический, графический и механический.

Аналитический метод заключается в определении площади земельного участка по результатам непосредственных или косвенных измерений линий, углов. Если площади земельных участков представляют собой простые геометрические фигуры (треугольники, многоугольники и т.п.), то их площадь определяют аналитически по размерам сторон треугольников, на которые следует разбить более сложные геометрические фигуры. В этом случае, если известны основания аi и высоты hi, то площадь S многоугольника определяется как сумма нескольких треугольников (рис. 2.28 б):

i= n

S = 0,5å ai hi

i= 1

(2.29) Если в треугольнике известны все стороны a, b и с, то для вычисления

площади можно воспользоваться другой формулой

S = 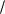P(P − a)( P − b)( P − c)

(2.30)

где Р – полупериметр треугольника.

Если в треугольнике известны две стороны а и b и угол между ними β, то площадь находится по формуле

S = 0,5ab sin β

(2.31) Площадь треугольника может быть найдена также и по известной сторо-

не а и двум углам α и β, прилежащим к ней:

S =	a 2
2(ctg α + ctg β )

(2.32) Если известны прямоугольные координаты вершин многоугольника

(рис. 2.28 а), то значение его площади может быть получено по формуле:

S = 0,5[ X1 (Y2 − Yn ) + X 2 (Y3 − Y1 ) + … + X n (Y1 − Yn−1 )]

(2.33)

или

S = 0,5[Y1 (X 2 − X n ) + Y2 (X 3 − X1 ) + … + Yn (X1 − X n− 1 )]

(2.34) Т.е. удвоенная площадь полигона равна сумме произведений абсциссы (ординаты) каждой из точек на разность ординат последующей и преды-

дущей (абсцисс последующей и предыдущей) точек.

Рис. 2.28. Аналитичесий (а) и графический (б) способы определения площади многоугольника

В зависимости от направления обхода значение площади может получиться со знаком минус. В связи с этим площадь надо брать по абсолютной величине.

Вычисление площади многоугольника по координатам его вершин следует выполнять для контроля по формулам (2.33) и (2.34).

Пример 2.17. Определение площади полигона по координатам его вершин. Исходные данные

Точки	1	2	3	4
Х, м	2156,847	1921,315	1541,242	1756,211
Y, м	4600,212	4563,842	4781,747	4763,226

Решение.

S = 0,5 [2156,847(4563,842 – 4763,226) + 1921,315(4781,747 – 4600,212) + 1541,242 (4763,226 – 4563,842) + 1756,211(4600,212 – 4781,747)] = 0,5[2156,847 (-199,384) + +1921,315 (181,535) + 1541,242(199,384) + 1756,211(-181,535)] = 46384,816 м2.

S = 0,5 [4600,212(1921,315 – 1756,211) + 4563,842(1541,242 – 2156,847) + 4781,747 (1756,211 – 1921,315) + 4763,226(2156,847 – 1541,242)] = 0,5[4600,212 (165,104) + +4563,842 (-615,605) + 4781,747(-165,104) + 4763,226(615,605)] = 46384,816 м2.

Ответы совпали !

Графический и механический методы используются для определения площадей на картографических изображениях.

Графический метод (рис. 2.28 б) предусматривает измерение на плане элементов сравнительно простых фигур (треугольника, прямоугольника, трапеции и др.), позволяющих затем вычислить площадь. Сложные фигуры разбивают обычно на треугольники, в которых измеряют основание и высоту. В некоторых случаях и площади криволинейного контура также разбивают на треугольники или другие простые фигуры.

Фигуры, на которые производят разбивку площадей объектов, должны быть по возможности крупными, мало вытянутыми, большая точность будет достигаться, например, при основании треугольника, равном его высоте, опущенной на это основание.

Часто в пределах измеряемой площади есть линии или углы, величины которых известны из результатов непосредственных измерений на местности. В этом случае необходимо разбивку привязать к этим линиям или углам, и использовать известные данные при вычислении площади.

Для повышения точности площадь фигуры следует определять не менее двух-трех раз, причем следует использовать разные разбивки. Расхождение в результатах определения площади по нескольким разбивкам не должно превышать 1:50 от величины площади всего участка.

Рис. 2.29. Определение площади фигуры с помощью палеток а – квадратная палетка; б – линейная палетка; в – точечная палетка

Механический метод определения площадей предусматривает использование палеток, ротометров, планиметров или других приборов.

Определение площадей с помощью палеток. Принцип определения площади с помощью палетки пояснен на рис. 2.29. Палетка представляет собой прозрачную основу, на которой построена сетка квадратов с известной стороной (квадратная палетка), серия параллельных линий с известным расстоянием между ними (линейная палетка), упорядоченная группа точек с известными расстояниями между ними (точечная палетка).

При использовании квадратной палетки для данного картографического материала определяют площадь элементарной ячейки (квадрата). Например, сторона квадрата равна 2 мм, масштаб карты 1:10000. В этом случае сторона квадрата на местности будет равна 20 м, а площадь – 400 м2. Палетку накладывают произвольно на фигуру и определяют число полных квадратов (N) и число всех неполных квадратов (n). Площадь определяют по формуле

S = 0,5 ( 2N + n ) S0

(2.35)

Пример 2.18. Определение площади с помощью квадратной палетки. Исходные данные (рис. 2.29 а) : N = 107, n = 49.

Решение.

S = 400 (107 + 49/2) = 52600 м2 (при S0 = 400 м2).

Похожий принцип реализуется и при использовании линейной палетки (рис. 2.29 в). В качестве единичной площади здесь выступает элементарная полоса длиной lo , например, 1 см при известном расстоянии а между линиями. В пределах контура фигуры измеряют длины линий посредине между нанесенными на палетку параллельными линиями, суммируют их и переводят через значение S0 в площадь. Если крайние границы контура образуют криволинейный треугольник, как это получилось на рисунке, то величину измеренного отрезка делят пополам. Т.е. площадь определяется в этом случае так же, как и площадь треугольника. В примере, который приведен ниже, это учтено для соответствующих отрезков.

Пример 2.19. Определение площади с помощью линейной палетки.

Исходные данные (результаты измерения в пределах контура криволинейной фигуры): (9,0:2 + 17,2 + 22,4 + 24,6 + 25,0 + 25,8 + 27,0 + 27,0 + 27,2 + 29,3 + 28,0 + 28,0 + 28,5 + 25,0 + 9,4:2 ) мм = 344,2 мм = 34,42 см.

Площадь определяется на карте 1:5000. Расстояние между линиями палетки 2 мм. Длина единичного отрезка принята равной 1 см. Следовательно, единичная площадь

Sо = 50 м · 10 м = 500 м2.

Решение.

S = (500 · 34,42) = 17210 м2.

При использовании точечной палетки (рис. 2.29 б) определяют площадь зоны влияния каждой точки, которая, вообще говоря, равна площади квадрата, как и в квадратной палетке. В контуре подсчитывают число точек (N) и умножают его на значение элементарной площади. При этом рекомендуется не принимать во внимание точки, совпадающие с контуром измеряяемой площади.

Пример 2.20. Определение площади с помощью точечной палетки. Исходные данные: Sо = 200 м2. N = 87 (рис. 2.29 б).

Решение.

S = 200 · 87 = 17400 м2.

Для повышения точности площадь определяют несколько раз (5 – 6 раз) с произвольной перестановкой используемой палетки в любое положение в том числе и с поворотом относительно ее первоначального положения. За окончательное значение площади принимают среднее арифметическое из результатов измерений.

Более точным и простым в использовании является способ линейной палетки, в котором суммируются отрезки палетки, пересекающие контур.

Определение площадей с помощью планиметра (рис. 2.30).

Планиметр был изобретен в 1850 г. русским конструктором П.А.Зарубиным.

Планиметр – это механический прибор, состоящий из полюсного рычага 1 с грузиком 3. Грузик содержит в центре иглу для закрепления его в устойчивом положении на столе. На другом конце полюсного рычага имеется сферическая шарнирная головка, которая свободно вставляется в гнездо 5 обводного рычага 2. На обводном рычаге имеется обводной штырь (игла) 4 и счетный механизм 6. Счетный механизм имеет дисковую шкалу 7 счета оборотов, счетное колесо 8, один оборот которого соответствует одному делению дисковой шкалы. Внешний ободок счетного колеса скользит по бумаге и за счет трения проворачивается и приводит в движение через червячную передачу дисковую шкалу. Со шкалой счетного колеса сопряжена шкала нониуса 9, по которой берут отсчет дробной части наименьшего деления шкалы счетного колеса.

Рис. 2.30. Планиметр 1- полюсный рычаг; 2 – обводной рычаг; 3 – груз; 4 – игла; 5 – гнездо; 6 – счетный

механизм; 7 – дисковая шкала; 8 – счетное колесо; 9 – нониус.

Полный отсчет (рис. 2.30) содержит четыре значащих цифры: 1-я – отсчет по шкале диска (3); 2-я – подписанное число на дисковой шкале до нулевого индекса нониуса (5); 3-я – число полных наименьших делений от ближайшей по возрастанию подписанной цифры счетного колеса до нулевого индекса нониуса (8); 4-я – ближайшее от нулевого индекса нониуса деление, совпа-дающее с делением шкалы счетного колеса (2). Таким образом, отсчет равен 3582.

Последовательность измерения площади фигуры.

1. Установить планиметр на карте таким образом, чтобы при обводе фигуры угол между полюсным и обводным рычагом не был меньше 30о и больше 150о. При этом колесо счетного механизма обязательно должно перемещаться по поверхности бумаги. Если фигура большая, т.е. не обеспе-

чивается поставленное выше условие, то ее следует измерять по частям. После подбора установки планиметра закрепить полюс нажатием на грузик и

вдальнейшем при измерениях не смещать.

2.Установить обводную иглу в точку фигуры, имеющей известную площадь и находящейся примерно в том же месте, что и измеряемая площадь. Такой фигурой может быть один, два или несколько квадратов километровой сетки системы прямоугольных координат карты. Если на картографическом материале отсутствуют фигуры известной площади, то можно их построить. Например, окружность известного радиуса, треугольник, квадрат и т.п. Взять начальный отсчет Ао по шкалам счетного устройства (например, Ао = 5783).

3.Аккуратно обвести фигуру с известной площадью с возвращением в начальную точку. Взять отсчет Во (например, Во = 5648).

4.Установить обводную иглу в точку фигуры с неизвестной площадью и взять начальный отсчет А (например, А = 4277).

5.Аккуратно обвести фигуру с неизвестной площадью с возвращением в начальную точку. Взять отсчет В (например, В = 4203).

6.Вычислить разности отсчетов

Со=Ао– Во и С = А – В: Со = 5783 – 5648 = 135; С = 4277 – 4203 = 74.

7. Вычислить площадь фигуры. Предположим, что известная площадь Sо

2			æ	SO C	ö
(Sо = 4 км ), тогда	S	=	ç
		ç	CO	.
			è	ø
В приведенном примере: S = (4 км2 · 74) : 135 = 2,193 км2.
Отношение Sо	/ Со = μ называется ценой деления планиметра. Таким
образом, S = μС.

Для повышения точности измерений площадь определяют несколько раз по схеме, приведенной выше. Целесообразно обвод площадей (известной и неизвестной) выполнять по часовой и против часовой стрелки, т.е. один полный прием измерения площади будет заключаться в двойном измерении. Обычно достаточно двух полных приемов. Окончательное значение площади находят как среднее арифметическое из результатов полных приемов измерений.

Если планиметр содержит два отсчетных устройства, то достаточно выполнить один полный прием, но при использовании во всех случаях двух отсчетных устройств, т.е. по каждой из точек брать по два отсчета, например,

Ао1, Ао2, Во1, Во2, А1, А2 и т.д.

До начала работы с планиметром необходимо выполнить его поверки в соответствии с указаниями, приводящимися в инструкции по пользованию, либо в другой соответствующей литературе.

При решении различных задач требования к точности определения площадей различные. В связи с этим в каждом случае требуется выбирать и способ определения площади.

В настоящее время выпускаются планиметры различных конструкций, в том числе и электронные планиметры, выдающие результаты измерений на механическое или электронное табло. На рынке геодезических приборов

Источник

Вы можете измерять расстояние между двумя местоположениями или длину пути, а также определять площадь многоугольника, нарисованного в сервисе “Google Планета Земля”.

Мы не гарантируем абсолютную точность измерений, особенно в областях с рельефом в трех измерениях и зданиями. Для достижения оптимальных результатов используйте вид сверху вниз.

Советы

При измерениях не учитываются перепады высот.
Эти инструкции относятся только к новой версии приложения “Google Планета Земля”. Подробнее о том, как измерить расстояние и высоту в приложении “Google Планета Земля Pro”…

Откройте сайт Google Планета Земля на компьютере.
Найдите нужное место или выберите его на глобусе.
В левой части экрана нажмите “Измерение расстояния и площади” . Будет установлен вид сверху вниз.
Нажмите на карту, чтобы задать точки измерения.
Чтобы удалить точку, в правой части экрана нажмите “Отменить” .
Чтобы завершить измерение расстояния, дважды нажмите на последнюю точку или нажмите “Готово” .

Данные по длине будут представлены справа.

Советы

Чтобы измерить площадь местоположения, завершите контур фигуры, установив связь с первой точкой. Сведения о площади будут приведены справа.
Чтобы открыть эти или другие инструкции, нажмите “Справка” .

Как скорректировать измерение

Как изменить единицы измерения

Измерив расстояние, выполните следующие действия:

В правом верхнем углу указано измеренное расстояние.
Рядом с единицей измерения нажмите “Развернуть” .
Выберите единицу измерения.

Чтобы изменить общие настройки, выполните следующие действия:

В левой части экрана нажмите на значок меню .
Нажмите “Настройки” .
В разделе “Формат и единицы измерения” выберите нужный вариант.

Как измерить высоту точки

Поместите курсор на карту в точку, высоту которой нужно измерить.
В правом нижнем углу указана высота.

Примечание. Разницу в высоте между двумя точками измерить невозможно.

Эта информация оказалась полезной?

Как можно улучшить эту статью?

Источник

Как измерить расстояние или площадь на карте?

Анонимный вопрос

2 марта 2018 · 149,4 K

Если требуется измерить расстояние по прямой на бумажной карте следует воспользоваться линейкой. Можно обычной измерить расстояние в сантиметрах, затем по формуле пересчета масштаба вычислить расстояние в километрах. Например расстояние на карте составило 2 см. Масштаб карты 1:200 000. т.е. в 1 см. расстояния на бумаге равно 200 000 см. расстояния на местности. т.е. 200000:100 = 2000 метров или 2 км. Карту с таким масштабом иногда называют двухкилометровкой. Вычисляем 2 см * 200000 : 100 : 1000 = 4 км. Самый крупный масштаб 1:25 000 (двухсот-пятидесяти-метровка). Если измеряем кривую изогнутую линию следует воспользоваться специальным инструментом – курвиметром. Установить его на ноль, и проведя колесиком инструмента по изгибам реки например, увидим на его индикаторе расстояние в сантиметрах. При отсутствии курвиметра можно измерить криволинейное расстояние разбив его некоторое количество прямых отрезков и сложив их длины. Точность такого способа плохая и ухудшается с уменьшением масштаба карты и количества прямых которые использовались для измерения.

4,2 K

Я удивляюсь, что до сих пор люди измеряют расстояние на бумажной карте курвиметром. Я уже лет 10 для этих целей… Читать дальше