Как найти площадь фигуры на квадратной решетке

Всем привет,мои юные и не очень любители пошуршать мозгами! 🧠

Сегодня поговорим о задачах с фигурами,но не простыми,а на квадратной решетке. 🤓

Такого рода задачи часто попадаются на ОГЭ,поэтому рекомендую дочитать ЭТО ЧУДО до конца 🙂

Длина средней линии трапеции

Решим задачу с этой самой длиной. На клетчатой бумаге 1×1 изображена вот такая трапеция:

Найдем длину ее средней линии.

Сосчитаем клеточки оснований:

7 снизу,3 сверху.

Их складываем.

А потом делим ответ на 2:

Ответ: 5

Расстояние от и до

Теперь про более странную задачу поговорим.

На клетчатой бумаге 1×1 отмечены три точки: A,B и C.

Нужно найти расстояние от точки A до середины отрезка BC.

Нужно ПРОСТО сосчитать три клетки до середины! ВСЕ!

Ответ: 3

Площадь ромба

На той же бумаге начертили ромб.

Нужно найти его площадь.

Как? Оч просто!

Нужно сделать из этого ромба прямоугольник:

А теперь посчитаем клеточки у сторон:

Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей.

Ответ: 20.

Площадь странной фигуры

На этой же (ОПЯТЬ?!ААА!) бумаге Вася начертил странную фигуру. А мы должны найти ее площадь…)

Теперь внимание! Нужно просто посчитать квадратики! Считаем…

Ответ: 11

Длина большей диагонали ромба

Опять ромб. Только теперь нужно найти не площадь,а длину большей диагонали.

Давайте посчитаем:

Ответ: 8

Повторим расстояния…

Опять нужно найти расстояние от точки А,до прямой BC.

Проведем прямую от точки между точками B и C.

А теперь проведем линию от точки A,до отрезка ВС.

Ответ: 1

Площадь параллелограмма

Найдем площадь параллелограмма.

Как ее искать?

Нужно умножить высоту на основание:

Ответ: 20

Длина средней линии треугольника

У нас есть вот такой треугольник:

Нужно найти длину его средней линии,параллельной стороне AC.

Для этого мы узнаем длину основания и разделим ее на 2.

Ответ: 2

Длина большего катета

Нам дан такой прямоугольный треугольник:

Нужно найти длину его большего катета.

Вспомним про стороны прямоугольного треугольника:

Катет b (основание) больше. Он имеет 10 клеток,а катет а 5.

Ответ: 10.

На этом все!

Ждите более сложные задания в следующем посте!

Способы решения задач на нахождение площадей фигур на квадратной решетке

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

«Решение задач – практическое искусство, подобное

плаванию, катанию на лыжах или игре на фортепиано;

научиться ему можно, только подражая хорошим

образцам и постоянно практикуясь»

Д. Пойя

Актуальность

Площадь – это одна из важнейших величин в геометрии. Без знания площадей невозможно решить множество геометрических задач, доказать теоремы. Площади фигур имели огромное значение много веков назад, но не утратили своего значения в современном мире. Понятие «площадь поверхности» используется во многих областях. Без него нельзя обойтись в строительстве, хирургии, авиационной промышленности, автомобилестроении, геологии и во многих других отраслях промышленности и видах деятельности человека.

Элементарными представлениями и простейшими умениями вычислять площадь несложной фигуры должен обладать любой современный образованный человек. Возможно, поэтому задачи такого плана содержатся в материалах государственной итоговой аттестации.

Например: задачи на квадратной решетке (клетчатой бумаге). У меня возникали вопросы: в чём заключается особенность таких задач, существуют ли специальные методы и приёмы решения задач на клетчатой бумаге.

Казалось бы, что увлекательного можно найти на клетчатой плоскости, т.е. на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Я научился вычислять площади многоугольников, нарисованных на клетчатом листке, познакомился с формулами для вычисления площадей фигур, приемами, позволяющими находить площади комбинированных фигур. Однако четкой классификации и структурирования задач на клетчатой бумаге по методам и способам решения я не встретил. Возможно, потому, что большинство таких задач считается «занимательными», и не так уж много авторов посвятило этой теме свои изыскания. Задался вопросом: существует ли универсальный метод вычисления площади многоугольника, расположенного на квадратной решетке.

Цель исследования заключается в расширении знаний о понятии площадь, поиске приёмов вычисления площадей многоугольников, расположенных на квадратной решетке, попытке выделить универсальный метод и создать обучающую брошюру в помощь ученику 7-9 класса.

Для достижения поставленной цели необходимо решить следующие задачи:

Подобрать необходимую литературу.

Проанализировать и систематизировать полученную информацию.

Найти различные приёмы вычисления площадей фигур, расположенных на клетчатой бумаге.

Классифицировать приемы.

Оформить работу в виде брошюры, создать электронную презентацию.

Предмет исследования: многоугольники на клетчатой бумаге

Объект исследования: приемы вычисления площадей многоугольников на клетчатой бумаге.

Методы исследования: изучение литературных источников и интернет-ресурсов, анализ и классификация информации, консультация с руководителем.

Гипотеза: возможно, многообразие многоугольников на бумаге в клеточку, отсутствие общих правил и методов вычисления площадей таких фигур, вызывают у школьников затруднения. Предположим, что при более внимательном исследовании приемов вычисления площадей фигур на клетчатой бумаге, мы убедимся в существовании универсального приема, позволяющего решить задачу при наличии достаточно простых геометрических сведений.

Теоретическая часть

1.1 Понятие площади

Площадь (S) – это величина, характеризующая размер той части плоскости, которая заключена внутри плоской замкнутой фигуры.

Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу.

Каждой плоской геометрической фигуре соответствует своя площадь. У пространственных фигур тоже есть соответствующая им площадь, называемая площадью поверхности.

Измерить площадь фигуры – это значит сравнить ее с площадью некоторой фигуры, принятой за единицу измерения площади.

Измерить площадь фигуры в Древней Греции означало построить квадрат, площадь которого равна площади данной фигуры. С тех пор всякое вычисление площади принято называть квадратурой.

Измерение площадей производится с помощью выбранной единицы измерения аналогично измерению длин отрезков. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Так, если за единицу длины принят сантиметр, то за единицу измерения площадей принят квадрат со стороной 1 см. Такой квадрат называется квадратным сантиметром и обозначается см². Если единицей измерения длины является 1 м, ему соответствует единица площади 1 м², если 1 мм, то единицей площади является 1 мм².

Пусть, например, за единицу измерения площади принят квадратный сантиметр. Тогда запись S =15 см² означает, что площадь фигуры равна 15 см², т.е. в данной фигуре квадрат со стороной 1 см укладывается 15 раз. Как правило, в задачах на клетчатой бумаге клетка условно принимается за квадратный сантиметр.

Невозможно в рамках одной работы рассмотреть весь спектр разнообразных фигур, изображенных на квадратной решетке (клетчатой бумаге). Ограничимся многоугольниками.

Вычисление площадей фигур по известным формулам

Чтобы решать задачи на вычисление площадей фигур на квадратной решетке, надо знать формулы, а также простые приёмы, о которых я расскажу.

Для начала выучим формулы площадей элементарных фигур. Они специально собраны в удобную таблицу.

Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой треугольник или привычно расположенный треугольник или многоугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, выяснить размеры по количеству клеточек и вычислить площадь. В этом легко убеждают приведенные в таблице задачи.

Таблица 1 – Формулы площадей

Название фигуры	Формула	Решение
Квадрат a a	2	Дано: Квадрат, a = 2 см Найти: S Решение: S квадрата 2 = 4 см 2 Ответ:
Прямоугольник b a		Дано: Прямоугольник, a = 2 см, b = 6 см Найти: S Решение: S прямоугольника Ответ:
Прямоугольный треугольник b a		Дано: прямоугольный треугольник, a = 3 см, b = 6 см Найти: S Решение: S треугольника Ответ:
Произвольный треугольник h a		Дано: произвольный треугольник, a = 8 см, h = 2 см Найти: S Решение: S треугольника Ответ:
Параллелограмм a b		Дано: Параллелограмм, a = 4 см, b = 6 см, ha = 4 см, hb = 6 см Найти: S Решение: S параллелограмма Ответ:
Трапеция a b		Дано: Трапеция, a = 4 см, b = 6 см, h = 2 см Найти: S Решение: S трапеции Ответ:
Ромб		Дано: Ромб, c = 2 см, d = 4 см Найти: S Решение: S ромба Ответ:

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Или фигуры, расположенной таким образом, что вычислить необходимые длины по клеточкам не представляется возможным.

Комбинированные фигуры

В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, игрушки и т.д. В геометрии вместо слова предмет говорят геометрическая фигура.

Слово «фигура» в переводе с латинского языка означает «внешний вид», «образ». Геометрическая фигура – совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.

Геометрические фигуры весьма разнообразны. Например: треугольник, квадрат, прямоугольник, и другие. Часть любой геометрической фигуры (кроме точки), также является фигурой. Объединение нескольких геометрических фигур, тоже будет являться геометрической фигурой.

Предметы простой формы в своей основе имеют одну геометрическую фигуру, а предметы сложной формы – несколько геометрических фигур. Более сложные объекты обычно называют комбинированными, имея в виду, что данный объект представляет сумму геометрических фигур. К таким объектам можно отнести и наши комбинированные фигуры.

Например:

Рисунок 1 – комбинированные фигуры

Как найти площадь нестандартной фигуры?

Способы вычисления площади сложных фигур

В работе представлены три способа нахождения площади комбинированной фигуры:

Разбиение комбинированных фигур на элементарные. Один из самых простых и доступных способов вычисления площадей был открыт Евклидом. При вычислении площадей он использовал простой прием, называемый методом разбиения. Разобьем эту фигуру на такие составляющие, о которых всё знаем, и найдем ее площадь как сумму площадей этих фигур.

Sф= S1+S2+S3

Площадь фигуры как разность площадей элементарных фигур. Берем фигуру в габаритные размеры, находим площадь фигуры как разность площадей элементарных фигур.

Sф= S – S1 – S2 – S3 – S4

Существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата.

, где B – узлы внутри фигуры Г – узлы на границе

Практическая часть

2.1 Задачи для самостоятельной работы

Задача 1: Найдите площадь трапеции, изображенной на клетчатой бумаге (рис. 1) с размером клетки 1 см×1 см. Воспользуйтесь различными приемами:.

Рисунок 1 – Трапеция

1 способ – Формула для вычисления площади трапеции

2 способ – Разбиение комбинированных фигур на элементарные фигуры. S_ф = S₁+S₂+S₃

3 способ – Площадь фигуры как разность площадей элементарных фигур.

S_ф = S – S₁ – S₂

4 способ – Формула Пика.

Задача 2: Найдите площадь окрашенной фигуры, изображенной на клетчатой бумаге (рис.2) . Размер каждой клетки равен 1 см х 1 см.

Рисунок 2 –Треугольник

Площадь находим по формуле Пика. Формула нахождения

Задача 3: Найдите площадь окрашенной фигуры, изображенной на клетчатой бумаге (рис.3) . Размер каждой клетки равен 1 см х 1 см.

Рисунок 3 –Прямоугольник

Площадь фигуры как разность площадей элементарных фигур. ФормуланахожденияSф= S – S1 – S2 – S3– S4

Задача 4: Найдите площадь окрашенной фигуры, изображенной на клетчатой бумаге (рис.4) . Размер каждой клетки равен 1 см х 1 см.

Рисунок 4 – Параллелограмм

Площадь находим по формуле Пика. Формула нахождения

Задача 5: Найдите площадь окрашенной фигуры, изображенной на клетчатой бумаге (рис.5) . Размер каждой клетки равен 1 см х 1 см.

Рисунок 5 – Фигура

Разбиение комбинированных фигур на элементарные фигуры. Формула нахождения Sф = S1 + S2 + S3

Заключение

В процессе исследования я изучил много справочной литературы, побывал на сайтах, прочитал некоторые книги в электронном виде. Я рассмотрел различные многоугольники, заданные на клетчатой бумаге. Научился вычислять их площадь различными методами. Убедился в том, что универсальным методом можно считать метод Пика, поскольку он приемлем практически для любых многоугольников, независимо от расположения. Недостатком этого метода считаю неточность результата при сомнительном положении узлов квадратной решетки. Лежит ли узел внутри контура или на границе. Для себя выделил в качестве универсального метода «метод разности площадей элементарных фигур».

Поделился своими наблюдениями в созданной брошюре с надеждой, что мой труд будет интересен другим ученикам.

Навыки, полученные в результате работы над данной темой, буду применять в обычных жизненных ситуациях, а также при дальнейшем глубоком изучении геометрии как науки.

Список использованных источников литературы

Бутузов, В. Ф. Геометрия. 7 – 9 классы: учеб. для общеобразоват. организаций. – М.: Просвещение, 2016. – 383 с.

Смирнова, И. М. Геометрические задачи с практическим содержанием: Учеб. пособие / И.М.Смирнова, В.А. Смирнов. – 2-е изд., доп. – М.: МЦНМО, 2015. – 216 с.

Трошин, В. В.Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008. – 288 с.

Интернет – ресурсы

Материалы сайта: http://kopilkaurokov.ru/matematika

Материалы сайта: http://www.edufuture.buz

Материалы сайта: http://www.matematikius.into

Приложение

Задача № 1: Найдите площадь комбинированной фигуры, изображенной на клетчатой бумаге (рис. 6) с размером клетки 1 см×1 см, используя формулу Пика.

Рисунок 6

Задача № 2: Найдите площадь комбинированной фигуры, изображенной на клетчатой бумаге (рис. 7) с размером клетки 1 см×1 см., см. используя метод сумм.

Рисунок 7

Задача № 3: Найдите площадь комбинированной фигуры, изображенной на клетчатой бумаге (рис. 8) с размером клетки 1 см×1 см, используя метод разности.

Рисунок 8

Задача № 4: Найдите площадь комбинированной фигуры, изображенной на клетчатой бумаге (рис. 9) с размером клетки 1 см×1 см. используя известные методы.

Рисунок 9

Задача № 5: Найдите площадь комбинированной фигуры, изображенной на клетчатой бумаге (рис. 10) с размером клетки 1 см×1 см известными способами нахождения площади.

Рисунок 10

Просмотров работы: 374

Как вычислить площадь многоугольника на рисунке, если размеры клетки равны 1 х 1?

Способы, которые подразумевают разбиение фигуры на прямоугольники и прямоугольные треугольники и нахождение площади “по частям”, отметаем сразу, ибо они достаточно трудоемкие по вычислениям.

В случаях, когда все вершины многоугольника лежат в узловых точках (т.е. на пересечении четырёх клеток решётки), площадь данной фигуры можно вычислить по формуле:

S = Г / 2 + В – 1,

где Г – количество узловых точек, находящихся на границе фигуры,

а В – количество узловых точек, лежащих внутри фигуры.

Эта формула называется формулой Пика.

И по этой формуле мы можем вычислить площадь любого многоугольника, в том числе и площади таких хорошо знакомых нам из школьной программы фигур, как треугольник, прямоугольник, параллелограмм, ромб, трапеция и т.д. Таким образом, множество соответствующих формул для площадей фигур можно заменить одной формулой Пика!

Вычислим площадь данной фигуры.

Г = 16 (синие точки),

В = 27 (черные точки).

S = 16 / 2 + 27 – 1 = 8 + 27 – 1 = 34.

 

Признаки равенства треугольников

 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

 3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.

 Признаки равенства прямоугольных треугольников

 1. По двум катетам.

 2. По катету и гипотенузе.

 3. По гипотенузе и острому углу

 4. По катету и острому углу

 Теорема о сумме углов треугольника и следствия из неё

 1. Сумма внутренних углов треугольника равна 180°.

 2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.

 3. Сумма внутренних углов выпуклого n-угольника равна 180°(n − 2).

 4. Сумма внешних углов n-угольника равна 360°

 5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.

 6. Угол между биссектрисами смежных углов равен 90°.

 7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.

 Основные свойства и признаки равнобедренного треугольника

 1. Углы при основании равнобедренного треугольника равны.

 2. Если два угла треугольника равны, то он равнобедренный.

 3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.

 4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, — то он является равнобедренным.

 Неравенство треугольника и следствия из него

 1. Сумма двух сторон треугольника больше его третьей стороны

 2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.

 3. Против большего угла треугольника лежит бOльшая сторона.

 4. Против большей стороны треугольника лежит больший угол.

 5. Гипотенуза прямоугольного треугольника больше катета

 6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то

  1) перпендикуляр короче наклонных;

  2) большей наклонной соответствует большая ´ проекция и наоборот

 Средняя линия треугольника.

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

 Теорема о средней линии треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна её половине.

 Теоремы о медианах треугольника

 1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.

 2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный

 3. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы

 Свойство серединных перпендикуляров к сторонам треугольника.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника

 Теорема о высотах треугольника.

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

 Теорема о биссектрисах треугольника.

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

 Свойство биссектрисы треугольника.

Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам

 Признаки подобия треугольников

 1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

 2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.

 3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.

 Площади подобных треугольников

 1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

 2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

 В прямоугольном треугольнике

 1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.

 2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.

 3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

 4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.

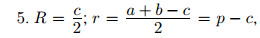
 где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно

 Теорема Пифагора и теорема, обратная теореме Пифагора

 1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

 2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный

 Средние пропорциональные в прямоугольном треугольнике

 Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу

 Метрические соотношения в треугольнике

 1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

 2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

 3. Формула для медианы треугольника. Если m — медиана треугольника, проведённая к стороне c, то

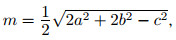
 где a и b — остальные стороны треугольника.

 4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

 5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.

 Формулы площади треугольника

 1. Площадь треугольника равна половине произведения основания на высоту.

 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

 3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

 4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.

 5. Формула Герона:

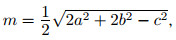
 где p — полупериметр; a, b, c — стороны треугольника.

 Элементы равностороннего треугольника

 Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной

окружностей равностороннего треугольника со стороной a. Тогда

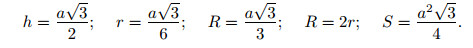
 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи	Обозначения	Формулы
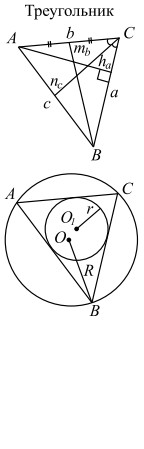	a, b, c — стороны; A, B, C — противолежащие им углы; ha, hb, hc — высоты, проведённые к соответствующим сторонам; na, nb, nc — биссектрисы, проведённые к соответствующим сторонам; ba и bc — отрезки, на которые делится биссектрисой сторона b; ma, mb, mc — медианы, проведённые к соответствующим сторонам; полусумма медиан; R — радиус описанной окружности; r — радиус вписанной окружности

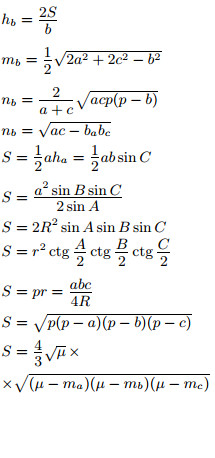Прямоугольный треугольник

Немного полезной информации

 В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных

на клетчатой бумаге или расположенных на координатной плоскости.

 Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.

Давайте вспомним эти формулы и разберём примеры их применения.

 Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):

   c² = a² + b²

 Площадь прямоугольного треугольника равна половине произведения его катетов:

   S =ab/2.

 Напомним, что у прямоугольного

треугольника есть прямой угол, равный 90°. Сторона напротив прямого

угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.

 На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.

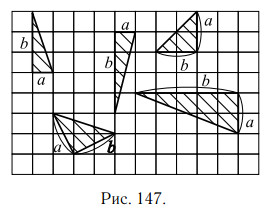
Задачи с решениями

 1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.

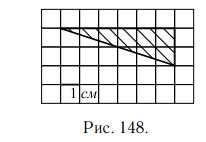
 Решение.

 Площадь прямоугольного треугольника равна половине произведения

его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем

по клеточкам), поэтому площадь

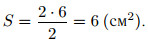
Ответ: 6

Площадь треугольника

Немного полезной информации

 Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне:

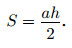
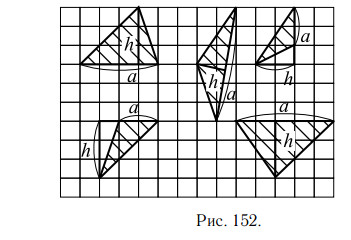
 На рисунке 152 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон a и высота, проведённая к этой стороне h.

 Как правило, удобно брать ту сторону, которая проходит по линиям

клетчатой бумаги (или же проходит параллельно осям координат).

Задачи с решениями

На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 153). Найдите его площадь в квадратных сантиметрах.

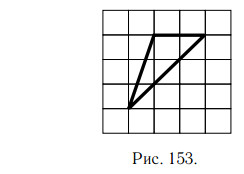
 Решение.

 1-й способ.

 Площадь произвольного треугольника равна половине произведения

длины его стороны (a) на высоту (h), проведённую к этой стороне. Проведём высоту h. Треугольник тупоугольный, поэтому высота проводится вне

треугольника.

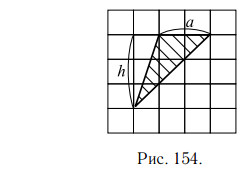
 На рисунке 154 сторона a = 2 см, высота h = 3 см

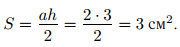
 Ответ: 3.

 Заметим, что так как клетки имеют размер 1 см × 1 см, то площадь

в квадратных сантиметрах получится, если мы будем по рисунку считать

размер отрезков в клетках. Поэтому единицы длины в этих задачах можно

и не писать.

 2-й способ.

 Достроим треугольник BCM до прямоугольного треугольника MCA

(см. рис. 155).

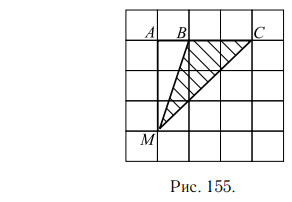
Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB.

Катеты первого из них равны 3 см и 3 см, катеты второго — 3 см и 1 см.

Площадь прямоугольного треугольника равна половине произведения

его катетов, следовательно,

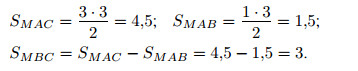
 Ответ: 3.

 Четырёхугольник

 

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

 Свойства и признаки параллелограмма

 1. Диагональ разбивает параллелограмм на два равных треугольника.

 2. Противоположные стороны параллелограмма попарно равны.

 3. Противоположные углы параллелограмма попарно равны.

 4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

 5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

 6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

 7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.

 Свойство середин сторон четырёхугольника.

Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.

 Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

 Свойства и признаки прямоугольника

 1. Диагонали прямоугольника равны.

 2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

 Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

 Формулы площади четырёхугольника

 1. Площадь параллелограмма равна произведению основания на высоту

 2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

 3. Площадь прямоугольника равна произведению двух его соседних сторон.

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

 Площадь прямоугольника равна произведению его смежных сторон:

    S = ab.

 На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

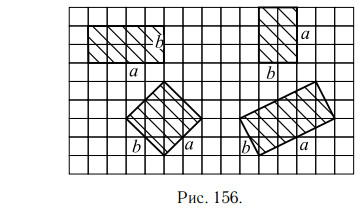
Задачи с решениями

 На клетчатой бумаге с клетками размером 1 см×1 см изображён прямоугольник (см. рис. 157). Найдите его площадь в квадратных сантиметрах.

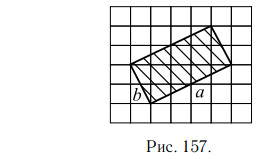
 Решение.

 1-й способ.

 Площадь прямоугольника равна произведению его смежных сторон a

и b. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник ABC с катетами AB = 2 и BC = 1 и гипотенузой

AC = b (см. рис. 158).

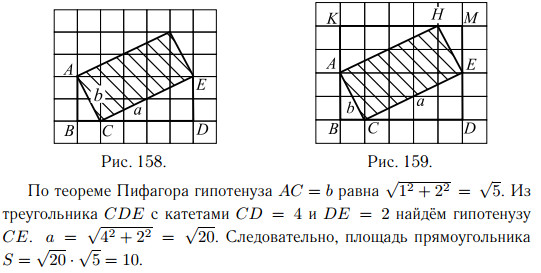
 Ответ: 10.

 2-й способ.

 Достроим прямоугольник ACEH до прямоугольника BKMD

(см. рис. 159). Чтобы найти площадь ACEH, нужно из площади прямоугольника BKMD вычесть площади прямоугольных треугольников

AKH, HME, EDC и ABC.

 Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников

(AKH и EDC) равна 4, а площадь каждого из двух маленьких треугольников (HME и ABC) равна 1. Площадь прямоугольника BKMD равна 4 · 5 = 20. Следовательно, площадь искомого прямоугольника будет равна 20 − 1 − 1 − 4 − 4 = 10.

 Ответ: 10.

 Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.

 Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

 Свойства и признаки ромба

 1. Диагонали ромба перпендикулярны.

 2. Диагонали ромба делят его углы пополам

 3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

 4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

 Площадь ромба равна половине произведения его диагоналей

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

 Четырёхугольник

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

 Свойства и признаки параллелограмма

 1. Диагональ разбивает параллелограмм на два равных треугольника.

 2. Противоположные стороны параллелограмма попарно равны.

 3. Противоположные углы параллелограмма попарно равны.

 4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

 5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

 6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

 7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.

 Свойство середин сторон четырёхугольника.

Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.

 Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

 Свойства и признаки прямоугольника

 1. Диагонали прямоугольника равны.

 2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

 Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

 Формулы площади четырёхугольника

 1. Площадь параллелограмма равна произведению основания на высоту

 2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

 3. Площадь прямоугольника равна произведению двух его соседних сторон.

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

 Площадь прямоугольника равна произведению его смежных сторон:

    S = ab.

 На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

Ромб

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

 Свойства и признаки ромба

 1. Диагонали ромба перпендикулярны.

 2. Диагонали ромба делят его углы пополам

 3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

 4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

 Площадь ромба равна половине произведения его диагоналей

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Трапеция

Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).

 1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.

 2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

 Замечательное свойство трапеции.

Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

 Равнобедренная трапеция.

Трапеция называется равнобедренной, если её боковые стороны равны.

 Свойства и признаки равнобедренной трапеции

 1. Углы при основании равнобедренной трапеции равны.

 2. Диагонали равнобедренной трапеции равны

 3. Если углы при основании трапеции равны, то она равнобедренная.

 4. Если диагонали трапеции равны, то она равнобедренная

 5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи	Обозначения	Формулы
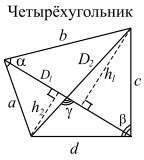	a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника.
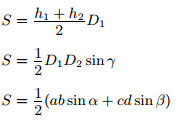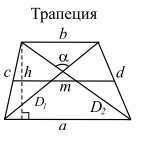	a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота

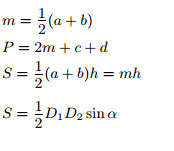 Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):

 На рисунке 168 приведены чертежи некоторых трапеций, у каждой из

которых показаны основания a и b и высота h.

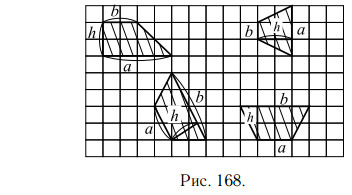
 Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

 Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

 Основные формулы

 Далее S — площадь фигуры, P — периметр, p — полупериметр.

  Площади круга и сектора

Площадь круга равна произведению числа π на квадрат радиуса:

    S = πR².

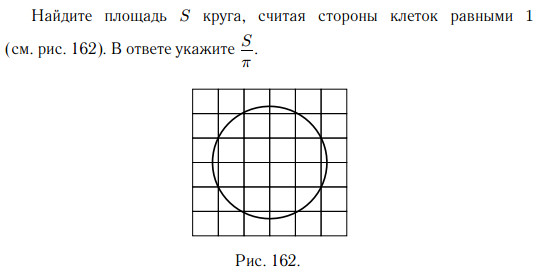
 Решение.

 Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)

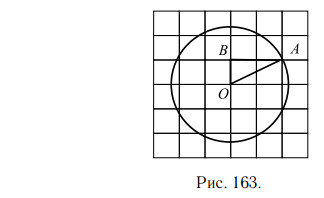
 Найдём гипотенузу по теореме Пифагора.

 Ответ: 5

 На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь

внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

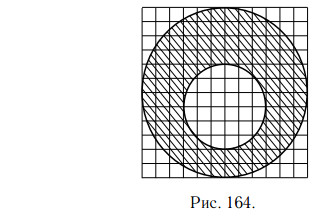
 Решение.

 Радиус R внутреннего круга — 3 клетки, его площадь равна πR² = 3.

Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна

π · (2R)² = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.

 Ответ: 9

Автор материала: А. Дронова (5 класс)

Опубликовано 17.07.18 в 21:56